基于纳米时栅传感器安装偏差的测量精度分析研究*

王合文，吴玉梅，郑方燕，但敏，樊星辰

(重庆理工大学机械检测技术与装备教育部工程研究中心，时栅传感及先进检测技术重庆市重点实验室，重庆400054)

基于纳米时栅传感器安装偏差的测量精度分析研究*

王合文，吴玉梅，郑方燕*，但敏，樊星辰

(重庆理工大学机械检测技术与装备教育部工程研究中心，时栅传感及先进检测技术重庆市重点实验室，重庆400054)

为了解析安装参数与测量精度的关系，根据纳米时栅的基本测量原理，构建出与动、定尺间距d0和正对面积变化量ΔS相关的数学模型。通过理论推导，分析了动尺在yz平面倾斜、xy平面偏转时会导致两路驻波幅值不等、相位偏移，从而给测量结果带来二次误差。实验结果表明通过调整动尺在yz平面与xy平面上的安装，对极内原始误差由4.86 μm降低至0.84 μm，证明动尺在yz平面倾斜、xy平面偏转为产生二次误差的主要原因。在行程200 mm测量范围内，传感器误差峰峰值为400 nm。实验结果验证了理论分析的正确性，该分析为传感器结构参数优化和实验方法的改进提供了有力的支撑，为进一步提升传感器精度提供了可靠的理论依据。

纳米测量;时栅;安装;误差理论

纳米技术与生物技术、信息技术并列为21世纪的三大科技，是21世纪高技术竞争的制高点［1］。而纳米位移测量技术及器件是纳米数控机床、极大规模集成电路专用设备和国防军工特殊需求等超精密高端装备的核心技术和关键功能部件，是实现纳米精度定位与控制的“眼睛”，直接决定和影响着主机的性能［2］。目前，国内外主要研究的是纳米光栅技术。其测量原理对制造工艺和加工工艺要求苛刻，在大面积的范围内对等周期细密栅线很难保证结构的均匀性和一致性制造［3－5］。因此，很难解决大量程与高精度之间的矛盾［6］。针对上述矛盾，作者所在团队在前期时栅研究的基础上提出了一种利用交变电场耦合的纳米时栅位移传感器［7－8］。利用时空转换理论［9－11］将空间位移转换成时间量测量，利用高频时钟脉冲作为计量基准来提高测量精度和分辨率［12］。

安装参数对传感器的测量精度有着直接影响，尤其在微纳米测量领域，任何微小的安装偏差都将严重影响传感器的测量精度。因此，研究纳米时栅传感器安装参数与误差规律之间的相互关系显得至关重要。

基于前期课题组对纳米时栅传感器测量理论、电场分布及信号处理方法的研究［7－8］，本文从传感器的结构与安装出发，建立与动、定尺间距d0和正对面积变化量ΔS相关的数学模型及安装模型，通过对模型的理论分析找出了动尺在yz平面倾斜及xy平面偏转时所引入的误差谐波成分，并通过实验得到验证。本研究对纳米时栅传感器参数优化和实验方法的改进具有理论指导意义。

1 纳米时栅工作原理

纳米时栅传感器由定尺和动尺部分组成，图1为纳米时栅传感器结构示意图，上面部分为分布有两排正弦极片的动尺，下面部分为分布两排方形极片的定尺。其中，定尺极片分别奇、偶相连并等间隔均匀分布，组成起始位置相差1/2极片宽度的A、B两相激励。

图1 纳米时栅传感器示意图

将定尺与动尺正对平行放置，形成沿x方向的左、右两组差动电容，并在奇、偶极片上分别施加大小相等，符号相反的正弦激励信号和余弦激励信号。

纳米时栅传感器可看成一个带负载的两组差动电容组合，任意一路的等效电路如图2所示。

图2 纳米时栅等效电路

根据电路的叠加定理，求得输出为:

式中:Zb1、Zb2分别为输出Uo后端负载ZL与C1、C2并联的阻抗，Z1、Z2分别为C1、C2容抗，U+、U_为大小相等，相位相反的激励信号。

设输入激励信号为 Ui=U+－U－，则式(1)可化为:

设在某一静态位置的时，C1、C2正对面积分别为S1、S2，动、定尺间距为d0，将电容公式C=εS/d和容抗公式Z=1/2πfC含参数带入式(2)，则单组输出为:

当电桥平衡时，电容C1、C2正对面积均为S0;动尺移动，电容 C1、C2正对面积分别减小和增大ΔS，此时输出为:

当传感器尺寸确定时，从式(4)可以看出输出Uo与激励Ui、电容正对面积变化量ΔS和动、定尺间距d0有关。

在两组定尺上分别施加A相正弦激励UiA与B相余弦激励UiB:

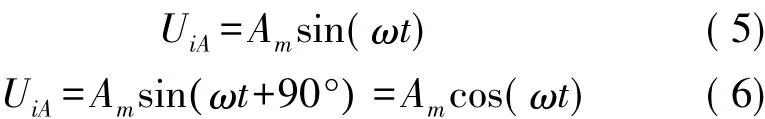
其中:ω为激励信号角频率，t为时间变量。

利用正弦函数变上下限积分方法［8］得出动尺上两路驻波信号为:

将耦合的两路驻波信号Uoa、Uob相加得到行波信号Ux:

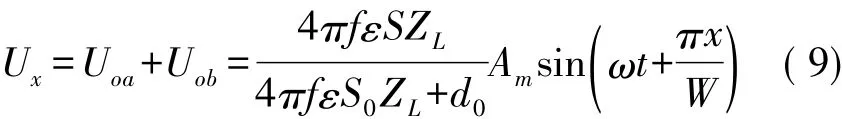
为便于后续讨论，令

将行波信号Ux与另一路相位固定频率相同的正弦信号Uy通过整形电路转换为方波，送入比相电路进行比相，利用高频时钟插补技术求得两路信号的相位差，最后通过FPGA处理即可得到传感器动尺与定尺之间的相对直线位移量。

2 误差理论模型

通过实验研究，现阶段对极内误差主要呈现为二次，因此需要对二次误差来源进行理论分析。通过分析，产生二次误差的主要原因为两路驻波的幅值不等和相位偏移。

2.1 两路驻波幅值不等

在测量过程中，两路驻波幅值不等将导致合成的行波失真。假设两路驻波幅值分别为 K1Am、K2Am，则合成的行波信号表达式为:

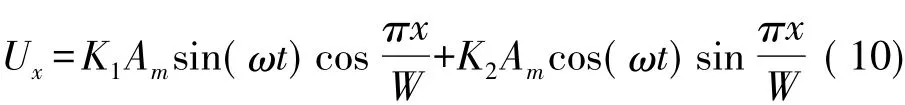
根据三角函数公式:

化简式(10)，可得:

式中:

且当x→0、W/2时x→x'。

从式(12)看出行波信号的幅值会随着cos(2πx/W)的引入在一个周期内呈现二次变化，在测量结果中也必将引入一个二次误差，其变化的峰峰值为:

2.2 两路驻波相位偏移

假设两路驻波的空间相位并非严格相差90°，其分别与标准相位的偏差为φ，则合成的行波信号表达式为:

同理，通过式(11)化简得:

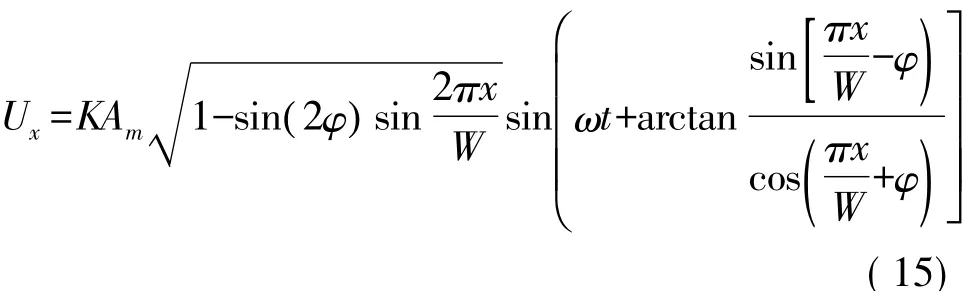
从式(15)看出测量结果必将由于sin(2πx/W)的引入而在一个周期内产生二次误差，峰峰值为:

2.3 仿真验证

通过上述理论分析，当两路驻波幅值不等、相位偏移时会给测量结果带来二次误差。为方便分析，设置ω=1 rad/s。当两路驻波幅值不等时，K1Am= 15 V、K2Am=22 V，φ=0 rad;两路驻波相位偏移时，KAm=22 V，φ=π/36 rad。利用MATLAB进行波形仿真，结果如图3所示。

图3 MATLAB仿真波形图

从图3的仿真波形可以看出，仿真结果与理论公式推导的结果相吻合。

3 安装误差分析

从上述的理论分析可以看出，测量结果中出现二次误差的原因是由于两路驻波幅值不等或相位偏移。而造成驻波幅值不等或相位偏移的主要原因为动尺安装上在yz平面倾斜或xy平面偏转。

3.1 yz平面动尺倾斜

以图1建立三维坐标动尺相对定尺在yz平面上有倾斜。假设在yz平面上相对于定尺有一个倾斜角α，如图4所示。

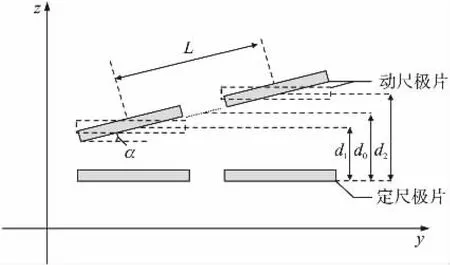
图4 yz平面动尺倾斜示意图

图2中，α为动尺偏转角度，d0为平行安装时动、定尺之间间距，L为两路动尺中心间距，d1=d0－Lsin(α/2)、d2=d0+Lsin(α/2)分别为偏转后动尺与定尺的等效间距。

在实际测量过程中，动尺如图4倾斜时动、定尺之间的正对面积S和间距d均会发生变化，为方便讨论现将标准安装等效为两路动尺分别与定尺平行，虚线框体为标准安装时的动尺。

由等效模型得A相正弦激励动尺对应的ΔS'为:

单路驻波信号表达式为:

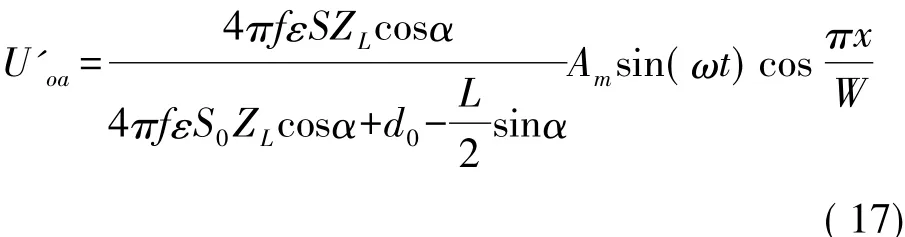
式中:d0＞Lsin(α/2)。

同理，可得另一路驻波信号表达式为:

即式(10)中:

则yz平面动尺倾斜时的行波表达式为:

故动尺在yz平面倾斜时会导致两路驻波幅值不等，从而引入二次误差。

3.2 xy平面动尺偏转

以图1建立三维坐标动尺相对定尺在xy平面上有个偏转。假设在想xy平面上相对于定尺有一个偏转角θ，如图5所示。

图5 xy平面动尺偏转示意图

图5中，l为动尺极片长度，θ为动尺相对于y方向的偏转角度，Δx为偏转引起的空间相位偏移量。则有:

当动尺相对于定尺在xy平面偏转时，其行波表达式为:

通过式(10)、式(19)化简得:

即动尺在xy平面偏转时，会导致两路驻波空间相位偏移从而引入二次误差。

4 实验验证与分析

为验证理论推导和仿真的正确性，判定二次误差的影响因子是否与分析一致，故还需要相应的实验验证。

4.1 实验平台搭建

根据纳米时栅传感器测量原理及结构的要求，搭建相应实验系统平台，具体实验平台如图6(a)所示。

图6 实验平台

定尺通过金属基座固定，动尺通过金属基座和美国Aerotech公司的ABL2000精密气浮直线导轨(精度达±0.75 um)相连，通过控制气浮导轨的移动来实现动、定尺的相对位移变化，通过电子显微镜和PI并联定位系统调节动、定尺之间的安装情况，利用PI并联定位系统的上位机软件读取并记录动尺初始安装参数。利用美国NI公司的LABVIEW产生标准激励信号UiA和UiB，其幅值为22 V，频率为20 kHz。用实验室团队设计的信号处理系统对动尺感应信号进行后续波形数据处理，并将位移数据送入计算机，从而得到纳米时栅的测量值。同时采用英国RENISHAW公司的ML100激光干涉仪(精度为±0.7 ppm)作为测量基准对时栅进行误差标定，得出误差曲线。

图6(b)所示为PCB工艺加工的传感器，其有效测量范围为200 mm。定尺为方形极片，动尺为正弦形极片，极片宽度均为0.2 mm，极片与极片之间的间隙均为为0.2 mm，单个测量周期即一个对极的长度为0.8 mm。

4.2 实验分析

纳米时栅的工作原理要求传感器的安装保证动、定尺之间的线性度和平行度，同时加载的激励信号也要有良好的一致性。但在实际测量过程中，这些影响因素往往难以达到理想状态。下面通过实验对这些影响因素造成的误差规律进行验证分析。通过前面的理论分析，当两路驻波幅值不等或相位有偏移量在一个周期内都会引入二次误差。

根据测量原理可知，当动、定尺极片平行时，单路驻波信号幅值最大，并且与另一路驻波信号最大值相等。同时，若动、定尺极片正对平行，当一路驻波幅值最大时，另一路驻波幅值理论为0 mV。

通过PI并联定位系统的上位机软件初始化安装并记录相关参数:α=0°，θ=0°。

在初始安装情况下，用气浮直线平台控制动尺与定尺在一个周期内反复移动，通过示波器观察得两路驻波最大幅值约为126.4 mV、134.7 mV;此时，静态采集数据与测量基准作差比较后得到的误差曲线如图7所示，初始误差峰峰值约为4.86 μm，主要表现为二次误差。根据式(19)、式(22)分析可知，二次误差主要是由于动尺的两种安装偏差造成。当动尺在yz平面倾斜时导致两路极片有效间距不相等，造成两路驻波幅值不等，从而在最终测量结果中引入二次误差;当动尺在xy平面与定尺相对有偏转时导致两路驻波空间相位偏移，从而也会引入二次误差。

用气浮导轨平台控制动尺与定尺在一个周期内来回移动，通过PI并联定位系统的上位机软件反复调整yz平面上动尺的倾斜角度，通过示波器观察两路驻波最大幅值。当调整至两路驻波最大幅值分别为130.8 mV、131.2 mV时，可基本认为其最大幅值相等，动尺与定尺平行。记录此时α=0.1°。采集所得误差曲线如图7所示，误差峰峰值约为2.43 μm，主要误差规律为一次和二次误差。其中一次误差主要要由单路驻波的幅值信号不相等造成［8］。调整动尺在yz平面的安装后所采集的误差与原始误差相比峰峰减小一半，即说明动尺在yz平面的会给测量结果带来二次误差。

通过反复调整动尺在xy平面上的偏转角度，用示波器观察两路驻波信号幅值。观察得Uoa最大幅值约为129.8 mV，Uob幅值约为0.4 mV;定尺移动半个周期位移时，Uoa的幅值减小至0.5 mV，Uob幅值增大至129.2 mV，记录θ=0.08°。此时可认为动尺与定尺基本平行正对。采集所得误差曲线如图7所示，误差峰峰值减小至0.84 μm，主要误差规律呈现为四次［8］，二次误差已基本消除。

图7 误差曲线图

上述实验已验证动尺在yz平面倾斜和xy平面偏转会给测量结果带来二次误差。从时空转换理论可知，空间域与时间域存在对应关系，即动尺在空间上安装造成的幅值不等、相位偏移，可通过调节时间域上的激励来使两路驻波幅值、相位相等。通过调整LABVIEW 4路激励信号的幅值和相位，使两路驻波幅值相等、相位一致，采集到的误差曲线如图7所示，峰峰值减小为0.98 μm，并且二次误差基本消除。

在前面理论分析得到实验验证的情况下，在200 mm量程范围内以采对极点的方式进行测量实验，最终测得传感器误差峰峰值为400 nm，如图8所示。

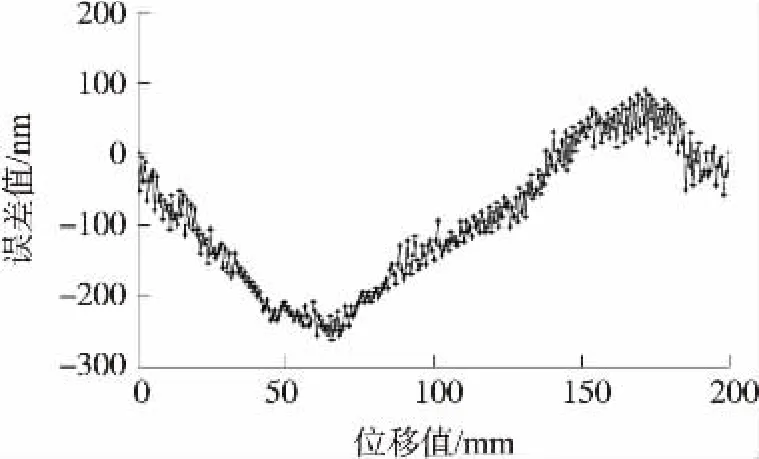
图8 传感器误差曲线

5 结论

本文从纳米时栅传感器的基本原理出发，构建出与动、定尺间距d0和正对面积变化量ΔS相关的数学模型。着重分析了由于两路驻波幅值不等、相位偏移所带来的误差成分。通过理论分析及实验验证，得出以下结论:①两路驻波幅值不等、相位偏移会给测量结果引入二次误差。②动尺安装在yz平面倾斜导致驻波幅值不等，在xy平面偏转导致两路驻波相位偏移。

实验结果验证了理论分析的正确性，该理论分析为传感器结构参数优化和实验方法的改进提供了有力的支撑，为进一步提升传感器精度提供了可靠的理论依据。

［1］ 王国彪，黎明，丁玉成，卢秉恒.重大研究计划“纳米制造的基础研究”综述［J］.中国科学基金，2010(2):70－77.

［2］ 陈本勇，李达成.纳米测量技术的挑战与机遇［J］.仪器仪表学报，2005，26(5):547－550.

［3］ Eurenius L，Hgglund C，Olsson E，et al.Grating formation by metal-nanoparticle-mediated coupling of light into waveguided modes［J］.Nature Photonics，2008，2(2):360－364.

［4］ 吕恒毅，刘杨，王延东，等.莫尔条纹正交偏差的智能补偿方法［J］.仪器仪表学报，2010，31(9):2075－2080.

［5］ Yoshimizu N，Lal A，Pollock C R.MEMS diffrac-tive optical nanoruler technology for tipbased nanofabrica-tion and metrology［J］.Micro Electro Mechanical Sys－terns，2009:547－550.

［6］ 国家自然科学基金委工程与材料科学学部，机械工程学科发展战略报告(2011－2020)［R］.北京:科学出版社，2010:288－315.

［7］ 刘小康，蒲红吉，郑方燕，冯济琴，于治成.纳米时栅位移传感器电场分布与误差特性研究［J］.仪器仪表学报，2013，(10): 2257－2264.

［8］ 刘小康，彭凯，王先全，朱革.纳米时栅位移传感器的理论模型与误差分析［J］.仪器仪表学报，2014，(5):1136－1142.

［9］ Liu X，Peng K，Chen Z，et al.A New Capacitive Displacement Sensor With Nanometer Accuracy and Long Range［J］.IEEE Sensors Journal，2016，16(8):2306－2316.

［10］彭东林，练俊君，陈锡候，等.基于时间序列的时栅转台误差修正研究［J］.重庆理工大学学报:自然科学版，2015，29(1):96－100.

［11］徐君，彭东林，万文略，等.时栅位移传感器中利用光电技术产生电行波信号的新方法［J］.传感技术学报，2007，20(3):532－535.

［12］于治成，郑方燕，冯济琴，等.纳米时栅传感器数字信号处理系统设计［J］.传感技术学报，2013(11):1548－1551.

王合文(1990－)，男，汉族，重庆人，硕士研究生，主要从事现代传感器技术研究，405788673@qq.com;

吴玉梅(1990－)，女，汉族，河北人，硕士研究生，主要从事现代传感器技术研究，844044212@qq.com;

郑方燕(1972－)，女，汉族，四川宣汉人，硕士，副教授，主要从事计算机辅助测试与仪器智能化的研究，发表论文20余篇，获专利5项，zfy@cqut.edu.cn。

Measurement Precision Analysis Based on Assembly Errors of a Nanometer Time-Grating Sensor*

WANG Hewen，WU Yumei，ZHENG Fangyan*，DAN Min，FAN Xingchen
(Engineering Research Center of Mechanical Testing Technology and Equipment，Ministry of Education，Chongqing Key Laboratory of Time Grating Sensing and Advanced Testing Technology，Chongqing University of Technology，Chongqing 400054，China)

In order to quantify the influences on measurement precision caused by assembly parameters，the gap d0and effective overlap area variation ΔS between the fixed ruler and the moving ruler are employed as independent variables to build mathematical models for measurement precision analysis based on the principles of nanometer time-grating sensors.Second harmonics errors are deduced in theory and tranced back in terms of unequal amplitude and phase deviation for two channels of standing waves when the moving ruler is not parallel to yz-plane or deviate from yz-plane.Experiment results show that the original errors for one pitch decrease from 4.86 μm to 0.84 μm by adjusting the assembly parameters of the moving ruler in the yz-plane and xy-plane，which demonstrates that second harmonics error is caused by un-parallel to yz-plane or deviation from yz-plane for moving ruler.The peak-to-peak value of the measurement error is 400 nm within 200 mm measurement range.The proposed theoretical analysis is valid by the experimental results，and provide strong supporting for optimizing the sensor’s structure parameters and improving experimental methods，which is very valuable for improving the measurement precision of nanometer timegrating sensor as reliable theory.

nanometer measurement;time grating;assembly;theory of error;

TH7

A

1004－1699(2017)02－0230－06

C:7230

10.3969/j.issn.1004－1699.2017.02.011

项目来源:重庆市基础与前沿研究计划项目(cstc2014jcyjA70002，cstc2016jcyjA0505)

2016－09－21 修改日期:2016－12－09