一个求解H-矩阵绝对值线性互补问题的罚方法
2017-04-13李园
李 园
(内蒙古民族大学数学学院,内蒙古通辽028043)
一个求解H-矩阵绝对值线性互补问题的罚方法
李 园
(内蒙古民族大学数学学院,内蒙古通辽028043)
考虑一类新的线性互补问题,即绝对值线性互补问题.通过构造与绝对值线性互补问题相等价的罚方程给出了一个求解此类绝对值线性互补问题的罚方法.并证明了当绝对值线性互补问题的矩阵为H-矩阵时算法的全局收敛性.最后,通过数值试验表明了该算法的有效性.
运筹学;绝对值线性互补问题;H-矩阵;罚方法;收敛
线性互补问题(简记作LCP(A,b))定义为,求x=(x1,x2,…,xn)T∈ℜn,使得:

其中A∈ℜn×n,b∈ℜn.
线性互补问题是运筹学与计算数学的一个交叉研究领域,已经广泛应用于力学、交通、经济、金融、控制等领域中出现的许多数学模型,例如障碍和自由边界问题、供应链问题、交通分配问题、经济均衡问题、非均衡博弈论等,这使得线性互补问题成为数学规划中的一个十分热门的研究课题.许多学者对线性互补问题的求解进行了深入的研究,提出了许多算法[1-5],例如:投影法、光滑牛顿法、非光滑牛顿法、松弛法、内点法、非光滑方程法、预条件迭代法等.进一步掌握和研究互补问题的各类算法不仅具有理论意义,而且具有实际意义.随着对LCP(A,b)这一领域研究的不断深入,Noor等[6]于2012年提出了一类新的线形互补问题,即绝对值线性互补问题,这也是本文要研究的问题.绝对值线性互补问题(简记作AVLCP(A,b))为:求向量x=(x1,x2,…,xn)T∈Rn,使得:
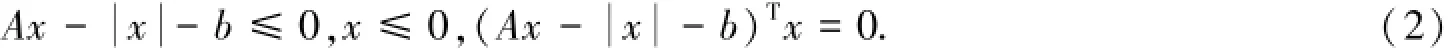

关于AVLCP(A,b)的研究,目前只有Noor等[6]提出的广义AOR迭代法和2014年李园等[7]提出的基于罚方程的广义牛顿法,该广义牛顿法的研究基于如下的非线形罚方程:求xλ∈ℜn,满足:

其中:λ>1是惩罚因子,k>0是参数,[u]+=max{ u,0}.对任意的y=(y1,y2,…,yn)T∈ℜn和任意实数α,有yα.鉴于此,对于AVLCP(A,b)的理论和算法的研究还有待进一步深入.因此,本文进一步研究求解AVLCP(A,b)的算法.
1984年,Glowinski[4]研究了一类与ℜn中变分不等式相等价的罚方程,证明了在变分不等式的矩阵为对称正定时罚方程的收敛性.2006年,Wang等[8]将美国期权问题转化成LCP(A,b),将文献[4]提出的罚方程进行了推广,证明了线性互补问题的矩阵为正定时新的罚方程的解收敛到互补问题的解.2008年,Yang等[9]利用文献[8]中构造的罚方程,在线性互补问题的矩阵为正定,主对角元素大于零,其余元素均小于等于零的条件下证明了当惩罚因子λ趋向于无穷大时非线性罚方程的解指数次收敛到线性互补问题的解.同年,Wang等[10]提出了一个带有扰动项的求解非线性抛物型互补问题的非线性罚方程,但是罚方程的解收敛到互补问题的解仍需正定性假设.鉴于上述罚函数方法的收敛性均依赖于线性互补问题的矩阵的正定性假设,李园等[11-12]将上述罚方法进行了推广,在线性互补问题的矩阵为P-矩阵时证明了罚方程的解指数次收敛到LCP(A,b)的解.
本文首先利用李园等[7]提出的非线性罚方程[4],证明了当AVLCP(A,b)中的矩阵A为H-矩阵时非线性罚方程[4]的解指数次收敛到AVLCP(A,b)的解.其次,通过数值试验表明了本文所提出的算法的有效性.
1 预备知识
为方便起见,本文给出如下记号.设A=(aij)∈ℜn×n为n×n实矩阵.矩阵A≥0当且仅当aij≥0,i,j=1,2,…,n.矩阵A的F-范数记为表示n维欧式空间.ℜn中所有向量均为列向量.向量x与y的内积记为xTy.对于实数p>1,向量的p-范数记为当p=2时,p-范数即为2-范数‖x‖=(xTx)12,2-范数也称为欧式范数.
定义1[1]设A=(aij)∈ℜn×n,若A的全部主子式均是正值,则称A为P-矩阵.
定义2[13]设A∈ℜn×n.
1)若aii≥0,i=1,2,…,n,aij≤0,i,j=1,2,…,n,i≠j,则称矩阵A为L-矩阵;
2)若aij≤0,i,j=1,2,…,n,i≠j,则称矩阵A为Z-矩阵;
3)设〈A›=(a~ij)∈ℜn×n,其中则称矩阵〈A›为矩阵A的比较矩阵.
定义[13]设A为Z-矩阵,A可逆且A-1≥0,则称A为非奇异的M-矩阵.
定义4[13]设A∈ℜn×n,如果A的比较矩阵是非奇异的M-矩阵,则称A为非奇异的H-矩阵,简称H-矩阵.
定义5[13]设A∈ℜn×n,如果:则称A为行对角占优矩阵.
定义6[13]设A∈ℜn×n,如果对任意的x∈ℜn,存在常数β>0,使得‖Ax‖≤β‖x‖成立,则称矩阵A有界.
引理1[1]若A∈ℜn×n为对角元素均为正数的H-矩阵,则A为P-矩阵.
引理2[7]设K是ℜn中的闭凸集,则存在常数ρ>0,x∈K是绝对值变分不等式(3)的解的充要条件是x∈K是方程:的解,其中PK为ℜn到闭凸集K上的投影.
引理3[3]A∈ℜn×n是P-矩阵的充要条件是:存在一常数c>0,对于任意向量x∈ℜn,存在一下表k= k(x),1≤k≤n,满足:
其中:xk表示x的第k个分量,(Ax)k表示Ax的第k个分量.
引理4 设A∈ℜn×n是P-矩阵.若则绝对值变分不等式(3)存在唯一解.
证明 唯一性的证明同文献[5]中定理2.4,下面只证存在性.设x∈K是绝对值变分不等式(3)的解,
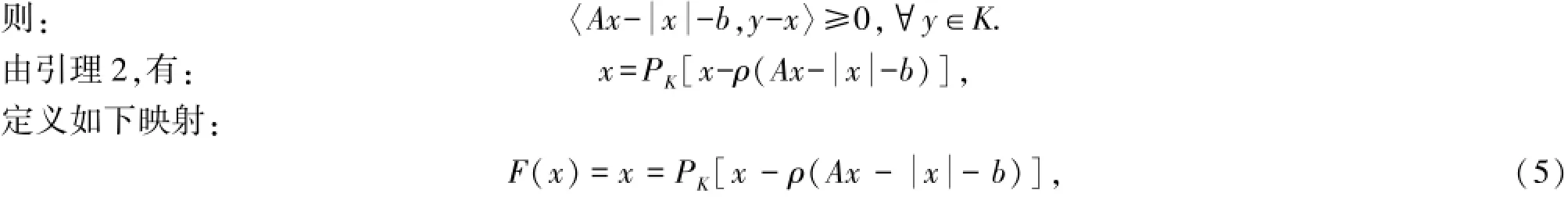
下面证明映射(5)存在不动点,只须证明映射(5)是紧映射即可.对于任意的x1≠x2∈K,
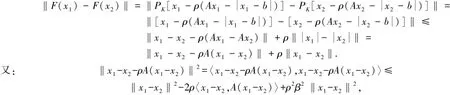
情况Ⅰ:若〈x1-x2,A(x1-x2)›=(x1-x2)1[A(x1-x2)]1+(x1-x2)2[A(x1-x2)]2+…+(x1-x2)n[A(x1-x2)]n中所有分量(x1-x2)i[A(x1-x2)]i,i=1,2,…,n均非负,则根据引理3,存在常数c>0,使得〈x1-x2,A(x1-x2)›≥c‖x1-x2‖2,故:
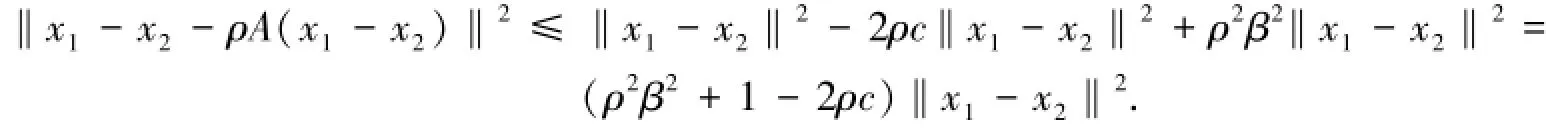
情况Ⅱ:若〈x1-x2,A(x1-x2)›=(x1-x2)1[A(x1-x2)]1+(x1-x2)2[A(x1-x2)]2+…+(x1-x2)n[A(x1-x2)]n中分量(x1-x2)i[A(x1-x2)]i,i=1,2,…,n既有正又有负,则不妨假设前k个分量
(x1-x2)i[A(x1-x2)]i≤0,i=1,2,…,k,后(n-k)个分量(x1-x2)i[A(x1-x2)]i≥0,i=k+1,k+2,…,n,则根据引理3,对于后(n-k)个分量,必存在一个分量(x1-x2)m[A(x1-x2)]m,m∈{k+1,k+2,…,n},使得存在常数c>0,有(x1-x2)m[A(x1-x2)]m≥c‖x1-x2‖2,则:
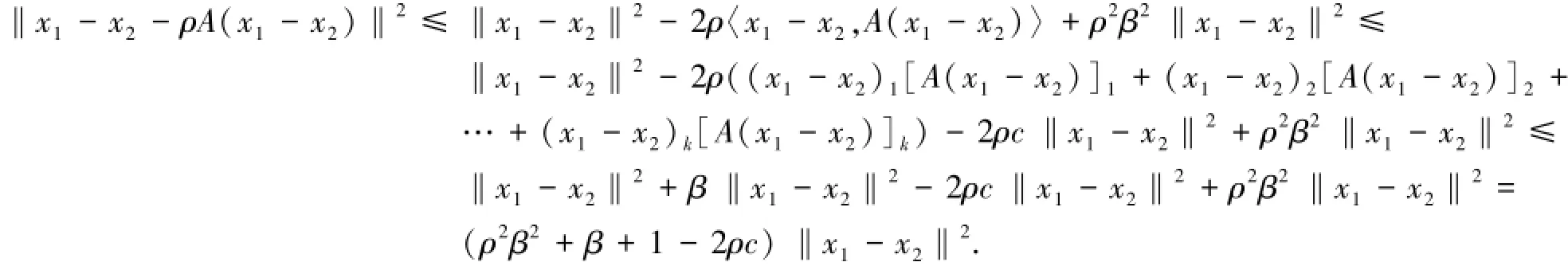
因此:
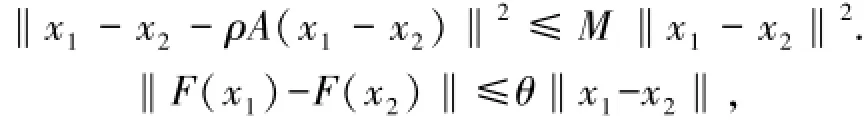
引理5(Hölder不等式)[12]设x,y∈ℜn,中p和q均大于1且满
关于矩阵A的F-范数‖·‖F与向量的欧式范数‖·‖的相容性,有如下结论:
引理6[4]设A∈ℜm×n,x∈ℜn,则
2 非线性罚方程(4)的收敛性质
本文将讨论非线性罚方程(4)的收敛性质,给出非线性罚方程(4)的解收敛于绝对值线性互补问题(2)的解.本节对AVLCP(A,b)中的矩阵A作如下假设:
(A1)A∈ℜn×n是有界的H-矩阵且行对角占优;
(A3)矩阵A的奇异值大于1.
根据引理1、引理4以及上面的假设,知绝对值线性互补问题(2)有唯一解.根据上面的假设,首先建立下面的定理.根据上述假设,可以得到如下结论:
定理1 设xλ=(u1,u2,…,un)T∈ℜn是非线性罚方程(4)的解.如果xλ满足如下条件之一:
i)xλ的分量均非正;ii)xλ仅有一个正分量,其余分量均非正;
iii)xλ有m(2≤m 则存在一个与n,xλ和λ均无关的正数C,满足: (A2)矩阵A的元素满足 证明 i)若xλ的分量均非正,这时[xλ]+=(0,0,…,0)T,于是则式(6)和 (7)显然成立;下面只证明情况iii),对于情况ii)类似可证. iii)若xλ有m(2≤m 将式(9)展开,得: 根据题设矩阵A为行严格对角占优及ui≥uj(1≤i 由定理1,可以得到下面的收敛性结论. 定理2 设x∈ℜn和xλ∈ℜn分别是AVLCP(A,b)和非线性罚方程(4)的解,其中xλ满足定理1的条件.若rλ=x+[xλ]-=(r1,r2,…,rn)T≤0且其任意两个不为零的分量ri和rj均存在一个与n, x,xλ和λ均无关的常数C>0,使得: 其中[xλ]-=-min xλ,0{},λ和k是非线性罚方程(4)中定义的参数. 证明 设根据[xλ]+和[xλ]-的定义,有xλ=[xλ]+-[xλ]-,于是: 其中rλ=x+[xλ]-.令ω=x-rλ,由rλ的定义知ω=x-rλ=[xλ]-≤0,于是ω∈K,在式(3)中令y=ω后,得: 将非线性罚方程(4)两端同时左乘rTλ后,有: 将式(11)和式(12)相加后得: i)若r1=r2=…=rn=0时 ii)若r1,r2,…,rn不全为零,不妨设r1,r2,…,rk≠0,rk+1=rk+2=…=rn=0,根据假设条件,对任意的1≤i 本节中,将通过数值例子来说明本文所建立的算法的有效性.运用Matlab 7.5进行计算,运行环境为: CPU为Intel(R)Core(TM)2×2.70GHz,内存为2.0GB. 当惩罚因子λ→+∞时,xλ→x∗,且‖x∗-xλ‖≤C/λ4. x∗=.在罚方程(4)中取k=1,解得: 当惩罚因子λ→+∞时,xλ→x∗,且‖x∗-xλ‖2≤C/λ2. 从例1、例2、例3可以看出,随着惩罚因子λ趋于无穷大时,罚方程(4)的解收敛到AVLCP(A,b)的解,这也正好验证了本文的结论. 本文首先利用李园等[6]提出的非线性罚方程(4),证明了当AVLCP(A,b)中的矩阵A为H-矩阵时非线性罚方程(4)的解指数次收敛到AVLCP(A,b)的解.其次,通过数值试验表明了本文所提出的算法的有效性. [1] COTTLE R W,PANG J S,STONE R E.The Linear Complementarity Problems[M].Academic Press,San Diego,CA,1992. [2] FACCHINEI F,PANG J S.Finite-dimensional variational inequalities and complementarity problems[M].Vol.I and II.New York:Springer,2003. [3] 韩继业,修乃华,戚厚铎.非线性互补理论与算法[M].上海:上海科学技术出版社,2006. [4] GLOWINSKI R.Numerical methods for nonlinear variational problems[M].New York:Springer-Verlag,1984. [5] 兰英,韩海山,岳织锋.线性互补问题的一个新的迭代算法[J].内蒙古民族大学学报(自然科学版),2014,29(6):624-626. [6] NOOR M A,IQBAL J,NOOR K I,et al.Generalized AOR method for solvung absolute Complementarity problems[J].Journal of Applied Mathematics,2012:1-14. [7] LI Y,HAN H S,YANG D D.A penalized-equation-based generalized Newton method for solving absolute-value linear complementarity problems [J].Journal of Mathematics,2014:1-10. [8] WANG S,YANG X Q,TEO K L.Power penalty method for a linear complementarity problems arising from American option valuation[J].Journal of Optimization Theory and Applications,2006,129(2):227-254. [9] WANG S,YANG X Q.Power penalty method for linear complementarity problems[J].Operations Research Letters,2008,36(2):211-214. [10] WANG S,HUANG C S.A power penalty method for solving a nonlinear parabolic complementarity problem[J].Nonlinear Analysis,2008,69(4): 1125-1137. [11] LI Y,HAN H S,LI Y M,et al.Convergence analysis of power penalty method for three dimensional linear complementarity problems[J].Intelligent Information Management Systems and Technologies,2009,5(3):191-198. [12] 李园,杨丹丹,韩海山.线性互补问题罚函数方法的收敛性分析[J].运筹与管理,2012,21(5):129-134. [13] 张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004. 责任编辑:时 凌 Apenalized Method for Solving H-Matrix Absolute-value Linear Complementarity Problems LI Yuan This paper considers a new class of linear complementarity problems,namely,the absolutevalue of the linear complementarity problems.We give a penalized method for solving such absolute-value inear complementarity problems by constructing a penalty equation which is equivalent to absolute-value inear complementarity problems and prove the global convergence when the matrix in absolute-value linear complementarity problems is a H-matrix.The numerical experiments show the effectiveness of this proposed algorithm. operations research;absolute value linear complementarity problem;H-matrix;penalized method;convergence O221.2 A 1008-8423(2017)01-0046-07 10.13501/j.cnki.42-1569/n.2017.03.011 2016-10-09. 内蒙古自然科学基金项目(2011MSO114);内蒙古民族大学科学研究基金项目(NMDY15017). 李园(1985-),男,硕士,主要从事变分不等式与互补问题的研究.


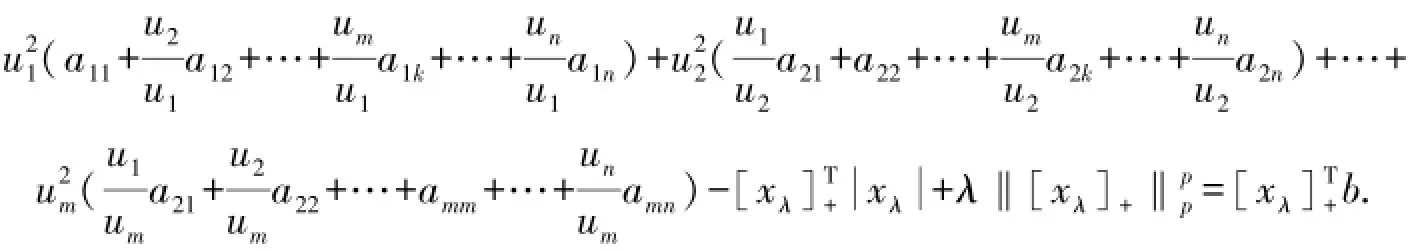
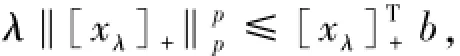




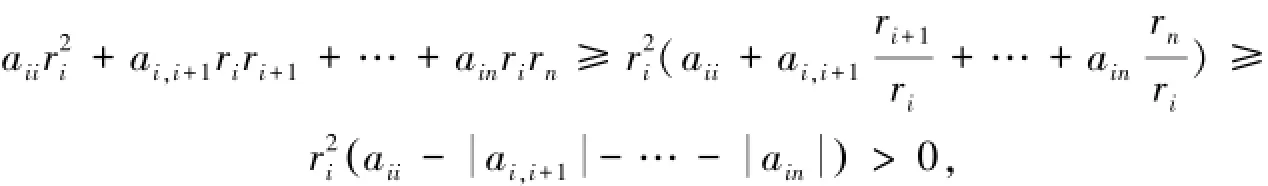


4 数值试验


5 总结
(College of Mathematics,Inner Mongolia University for Nationalities,Tongliao 028043,China)
