求解凸极小化问题的一种带预校正步的分解方法

李小蓉

(重庆师范大学数学科学学院，重庆401331)

求解凸极小化问题的一种带预校正步的分解方法

李小蓉

(重庆师范大学数学科学学院，重庆401331)

针对三个变量的可分离凸优化问题，提出了一种带预校正步的交替方向分解方法.与交替方向乘子法和预校正近似乘子法相比，该算法同样使用了增广拉格朗日函数，并且对偶变量进行了两次迭代.不同于之处在于，这种算法推广到了三个变量的情况.在系数矩阵是列满秩及拉格朗日函数有鞍点的假设下，该算法是收敛的.

凸优化问题；交替方向乘子法；预校正步

分解方法对于解决凸优化问题是有效可行的方法.通过分解，将原问题分解为多个子问题进行求解.在多区域电力系统分析、网络设计、多原则设计优化模型等领域中，经常遇到各种问题，使得提出一个比较好实施的分布式计算框架显得尤为重要.本文针对三个变量的可分离凸优化问题进行研究[1]，形式如下:

问题(1)的增广拉格朗日函数Ψ:Rn×Rs×Rm→(－∞，＋∞]定义如下:

其中:〈·，·›表示内积，λ是约束A1x1＋A2x2＋A3x3＝b相应的拉格朗日乘子，c是罚因子.

问题(1)的对偶问题为:

其中:θ(λ)＝inf{L(x1，x2，x3，λ):x1∈χ1，x2∈χ2，x3∈χ3}，分别为原问题和对偶问题的最优

解，鞍点最优性条件为:

针对两个变量的可分离凸优化问题，在1975年，R.Glowinsk[2]和D.Gabay[3]等人提出了一种算法，即交替方向乘子法(alternating direction method of multiplier，ADMM).这种算法的主要迭代格式如下:

在矩阵A1，A2满足列满秩及拉格朗日函数L(x1，x2，λ)有鞍点的假设下，ADMM算法是收敛的.交替方向乘子法是一种简单但功能强大的算法，所以被广泛应用于各个领域，详情可见文献[4－11].

针对三个变量的可分离凸优化问题，在2012年，D.Han，X.Yuan，W.Zhang[12]针对三个变量的可分离凸优化问题，提出了一种基于ADM的分裂法，将其转化成一个等价的具有可分离结构变分不等式问题.假设凸优化问题的解集是非空的，且约束条件的系数矩阵是满秩的，在这种假设条件下，证明了算法的全局收敛性.基于ADM的分裂法主要迭代格式如下:

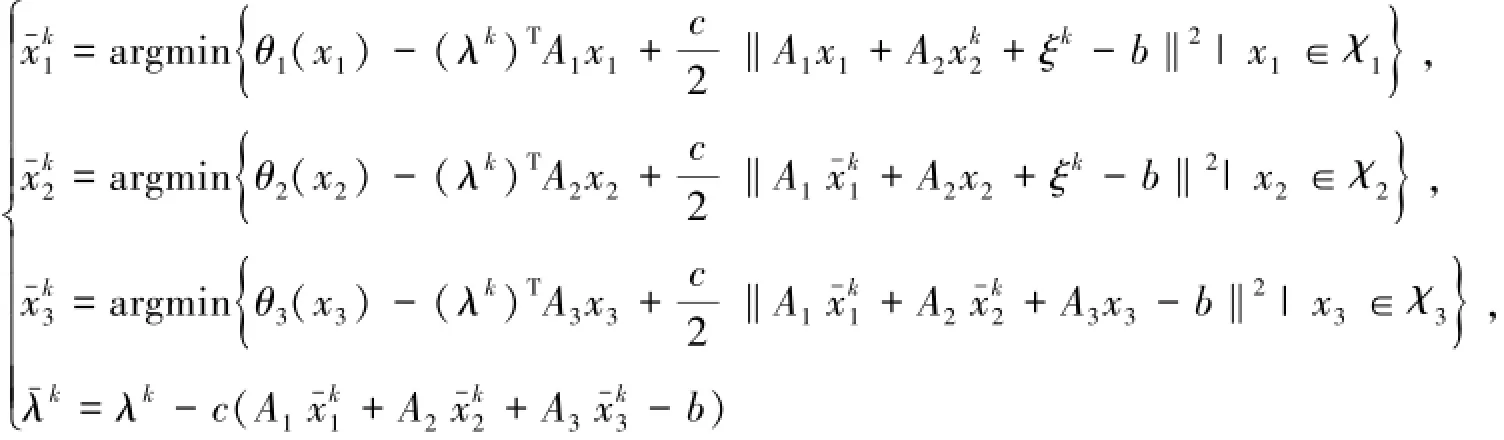
通过计算:

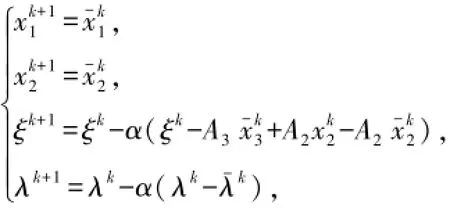
1994年，Chen和Teboulle[13]针对两个变量的可分离凸优化问题，提出了一种可分方法，即预校正近似乘子法(predictor－corrector proximal multiplier method，PCPMM).预校正近似乘子法的主要算法如下:

在拉格朗日函数有鞍点的情况下，PCPMM算法是收敛的.与交替方向乘子法的不同之处在于，PCPMM算法用邻近项替代了增广项，关于对偶变量进行了两次迭代.从迭代过程可以看出的计算是并行的.在上述两种算法的基础之上做出了一些改进，提出了一种预测校正交替方向乘子法(predictor－corrector alternating direction method of multiplier，PCADMM).

与预校正近似乘子法相比，在极小化时采取不同的格式，去掉了二次邻近项而直接用的增广项.算法的主要迭代格式如下:

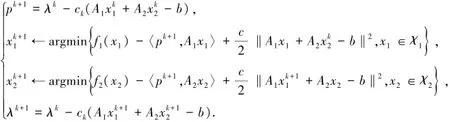
在矩阵A1，A2满足列满秩及拉格朗日函数L(x1，x2，λ)有鞍点的假设下，ADMM算法是收敛的.为了使得算法的应用更加广泛，将上述算法推广到了三个变量的可分离凸优化问题，即EPCADMM.该算法的证明与PCADMM算法的证明相似，但是终止准则发生了变化.在PCADMM中，终止准则为但是在EPCADMM算法中，若则算法停止.

1 推广的预测校正交替方向乘子法

步骤2 计算:

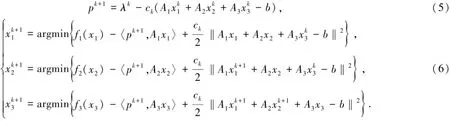
步骤3 乘子更新:

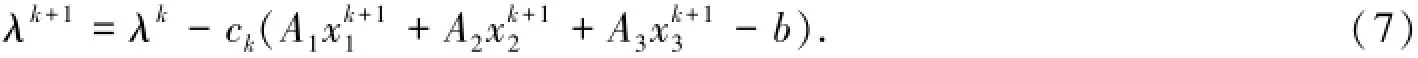
2 收敛性证明

对于问题(1)，通过引用一阶最优性条件和鞍点最优性条件[4，14－16]，我们很容易可以看到，求解问题(1)等价于求解变分不等式的一个解.

在这里，

1)该铁矿石为低硅低硫磷的酸性富铁矿，矿石氧化严重，有用矿物以磁铁矿为主，次为褐铁矿、假象赤铁矿，矿物组成较复杂。磁性分析表明，该矿磁性良好，可通过弱磁选实现去杂提纯的目的。

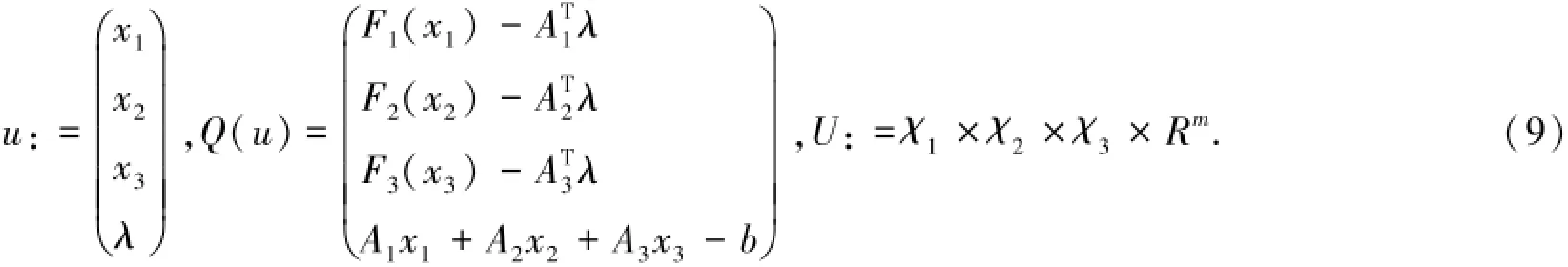
用VI(U，Q)表示VI(8)～(9).用u∗表示VI(8)～(9)的解，在假设条件下，解集u∗是非空的.在这一部分，对推广的预测校正交替方向乘子法的收敛性进行了证明.

证明 假设蕴含着:

由EPCADMM算法的式(5)和式(7)两个式子，可以得到λk＋1＝pk＋1＝λk.

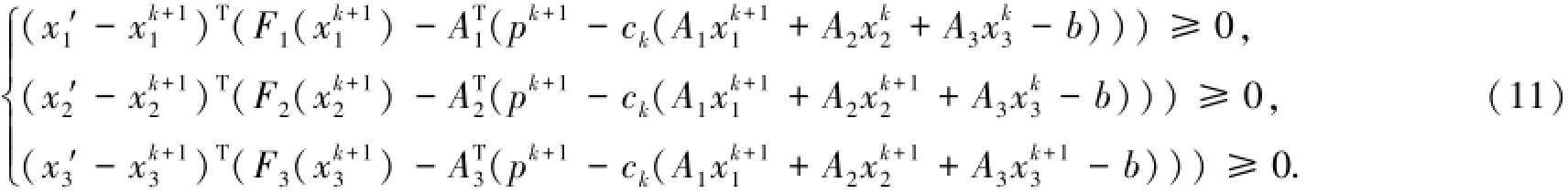
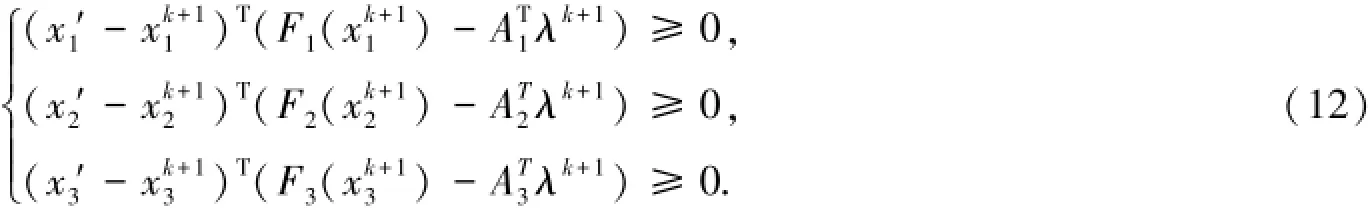
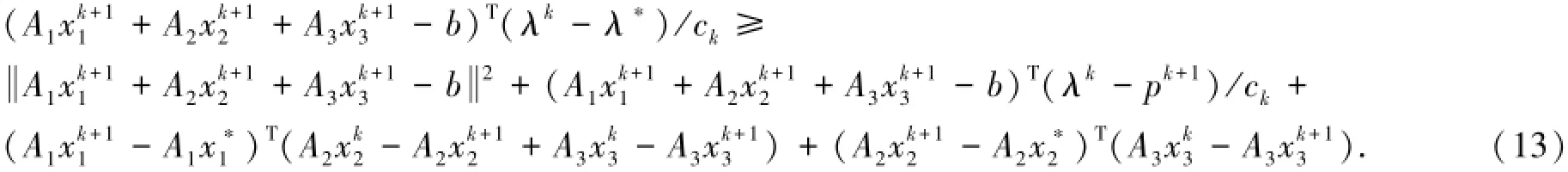
另一方面，在式(12)中，将xi′置为，得到:

同理，可以得到:

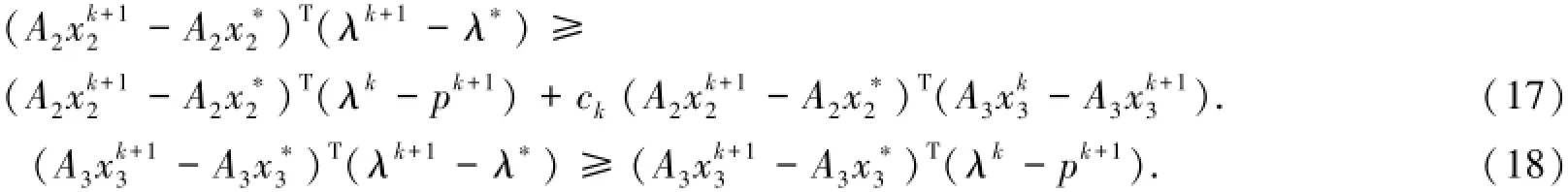
将式(16)～(18)加起来，可以得到:

因为λk＋1－λ∗＝λk－λ∗＋λk＋1－λk，对上式进行整理，得到:

这就完成了证明.

以下的等式显然是成立的.

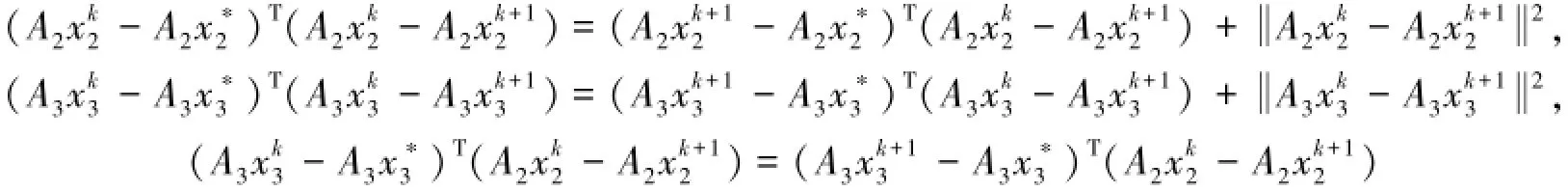
将以上三个式子加到式(13)中，可以得到:

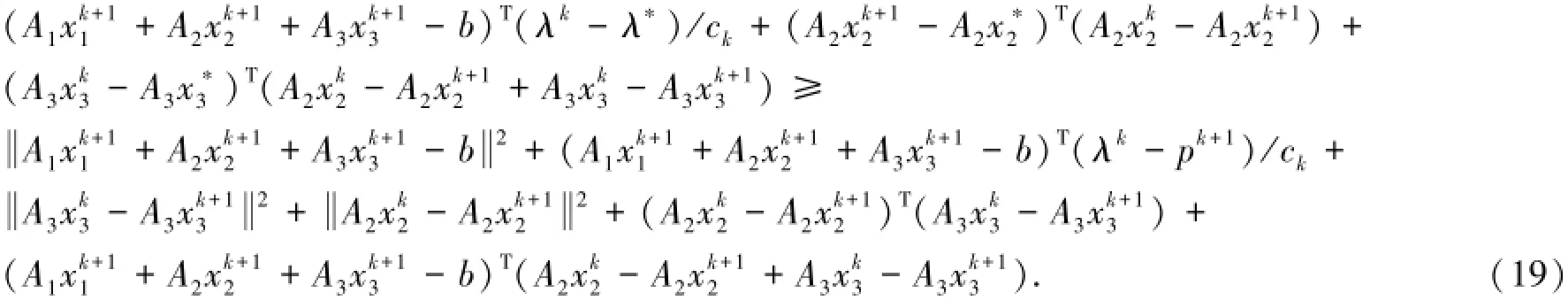
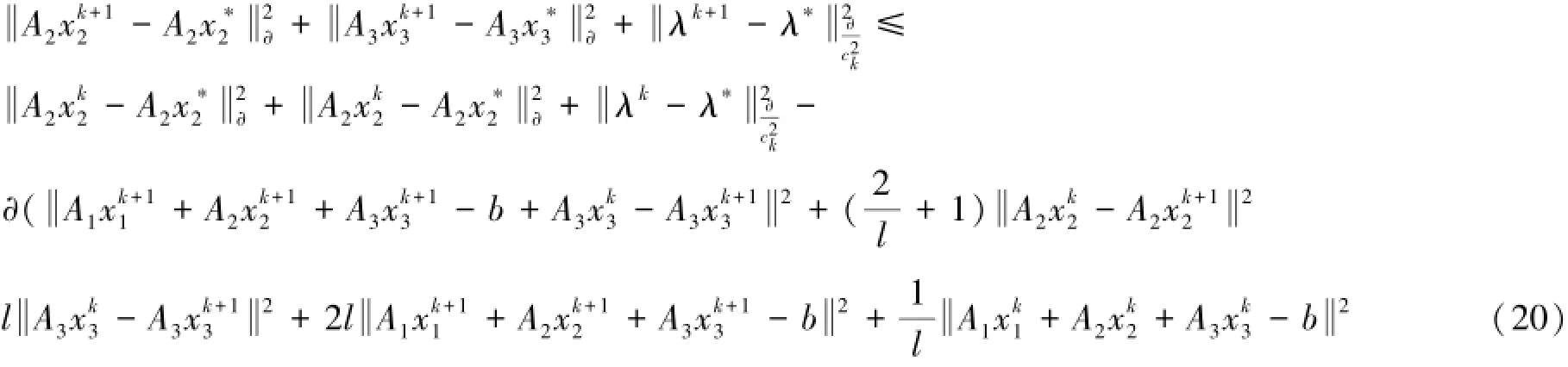
证明 下面的等式显然成立，

由此，可以得到:

通过式(18)、式(5)、式(7)可以得到上述不等式.对于任意的向量u、v和任意的正参数l>0，有:2uTv≤l因此，引理3得证.

证明 由式(20)，可以推出:

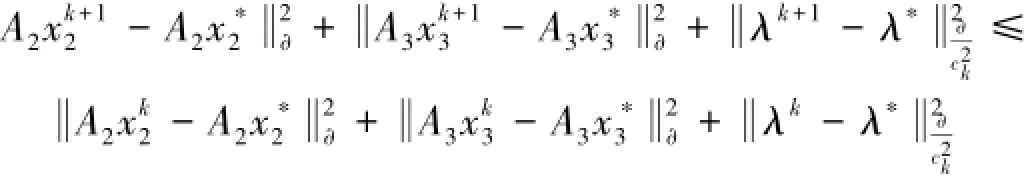
对所有的k(k＝0，1，…)求和，可以得到:

从上式，可得出:

因为A1、A2、A3满秩，所以序列仅有一个聚点.因为序列收敛到为VI(8)～(9)的一个解，引理4得证.

[1] BOYD S，PARIKH N，CHU E，et al.Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers[J].Foundations and Trends in Machine Learning，2010，3(1):1－122.

[2] GLOWINSKI R，LETALLEC P.Augmented lagrangian and operator splitting methods in nonlinear mechanics[M].Philadelphia:SIAM Studies in Applied Mathematics，SIAM，PA，1989.

[3] GABAY D，MERCIAR B.A Dual Algorithm for the solution of Nonlinear Variation Problems via Finite－element Approximations[J].Computers and Mathematics with Application，1976，2(1):17－40.

[4] CHEN C H，HE B S，YUAN X M.Matrix completion via alternating direction method[J].IMA J Numer Analysis，2012，32(1):227－245.

[5] ECKSTEIN J，BERTSEKAS D P.On the Douglas－Rachord splitting method and the proximalpoint algorithm for maximal monotone operators[J]. Math Program，1992，55(3):293－381.

[6] ESSER E.Applications of Lagrangian－Based alternating direction methods and connections to split Bregman[J].Cam Report，2009，9:31－36.

[7] HE B S，XU M H，YUAN X M.Solving large－scale least squares covariance matrix problems by alternating direction methods[J].SIAM J Matrix Analy Appli，2011，32(1):136－152.

[8] SETZER S，STEIDL G，TEBUBER T.Deblurring Poissonian images by split Bregman techniques[J].J Visual Commun Image Repres，2010，21 (3):193－199.

[9] SUN J，ZHANG S.A modified alternating direction method for convex quadratically constrained quadratic semidefinite programs[J].European J Oper Res，2010，207:1210－1220.

[10] TAO M，YUAN X M.Recovering low－rank and sparse components of matrices from incom－plete and noisy observations[J].SIAM J Optim，2011，21(1):57－81.

[11] 李慧.解凸优化问题的一类修正线性近似交替方向法[J].重庆工商大学学报(自然科学版)，2015，32(4):23－27.

[12] HAN D，YUAN X，ZHANG W.An ADM－based splitting method for separable convex programming[J].Computational optimization and applications，2013，54(2):343－369.

[13] CHEN G，TEBOULLE M.A proximal－based decomposition method for convex minimization problems[J].Mathematical Programming，1994，64 (1/3):81－101.

[14] BAZARAA M S，SHERALI H D，SHETTY C M.Nonlinear programming[M].Belmunt:Athena Scientific，2006，163－235.

[15] HAN D，KONG W，ZHANG W.A Partial Splitting Augmented Lagrangian Method for Low Patch－Rank Image Decomposition[J].Journal of Mathematical Imaging and Vision，2014，51(1):145－160.

[16] HAN D，YUAN X.A Note on the Alternating Direction Method of Multipliers[J].Journal of Optimization Theory and Applications，2012，155(1): 227－238.

责任编辑:时 凌

A Decomposition Method with Predictor－corrector for Solving Convex Minimization Problems

LI Xiaorong
(School of Mathematical Sciences，Chongqing Normal University，Chongqing 401331，China)

For the block－separable convex optimization problem of three variables，we proposed a decomposition method with a predictor－correction step.Compared with the alternating direction method of multiplier and the predictor－corrector proximal multiplier method，the algorithm also uses the augmented Lagrangian function and two iterations are made for the dual variables.The difference is that this algorithm is extended to three variables.Under the assumptions that the matricesare full－column－rank and the Lagrangian function has a saddle point，the algorithm converges.

convex programming problem；alternating direction method of multiplier；predictor－corrector

O224

A

2016－12－06.

国家自然科学基金项目(61263020).

李小容(1990－)，女，硕士生，主要从事计算数学的研究.