基于多值量化的混沌扩频序列及其性能分析*

于一丁,王永川,王长龙

(军械工程学院 无人机工程系，河北 石家庄 050003)

基于多值量化的混沌扩频序列及其性能分析*

于一丁,王永川,王长龙

(军械工程学院 无人机工程系，河北 石家庄 050003)

为了分析基于多值量化的混沌扩频序列的性能，以Chebyshev混沌映射为例，结合其概率密度分布函数的特点给出对其进行多值量化的方法。仿真分析多值量化混沌序列的平衡性和相关性，在高斯白噪声信道中对传统二值量化混沌序列和多值量化混沌序列扩频通信系统进行误码率仿真，并从低检测概率和低利用概率两个角度对多值量化混沌序列的抗截获性能进行分析。仿真结果表明多值量化混沌序列的误码率性能更好，其抗截获性能也有所提高。

混沌序列；多值量化；抗截获

0 引言

混沌现象是非线性动态系统中出现的确定性的类随机过程,这种过程具备高度的初值敏感性,非周期又不收敛。通过混沌映射可以生成大量具有尖锐自相关性、近似正交互相关性、类噪声的混沌序列[1]。相比传统的扩频序列如m序列、Gold序列等，混沌序列具有更好的伪随机性、更高的复杂度和抗截获能力，更加适合作为扩频码应用到扩频通信系统中[2]。

目前针对混沌序列的生成和优选方法国内外已经做过大量研究[3-5]，但仍存在一些问题：由混沌映射生成的混沌序列通常要经过数字量化处理后才能应用于扩频通信系统中，目前对混沌序列通常采用二值化处理，常用的方法有门限量化法[6]、比特抽取量化法[7]、中值量化法[8]等，但在二值化的过程中混沌序列会损失大量信息。为了改善混沌扩频序列的性能，本文将多值量混沌序列作为扩频码应用于扩频通信系统中，以Chebyshev混沌映射为例，将传统二值量化混沌序列和多值量化混沌序列应用于直接序列扩频(DSSS)系统中并进行仿真，仿真结果表明多值量化混沌扩频序列的性能优于传统的二值量化混沌扩频序列，更加符合扩频通信系统的要求。

1 混沌扩频通信系统

混沌扩频通信系统的基本原理和传统直接序列扩频系统类似，只是将伪随机序列换成混沌序列，其基本原理是将信源数据用混沌序列进行扩频调制，调制之后信源数据的频谱被扩展并通过天线传入信道，在接收端则采用与发送端同步的混沌序列进行相关解扩恢复数据。图1为混沌扩频通信系统框图。

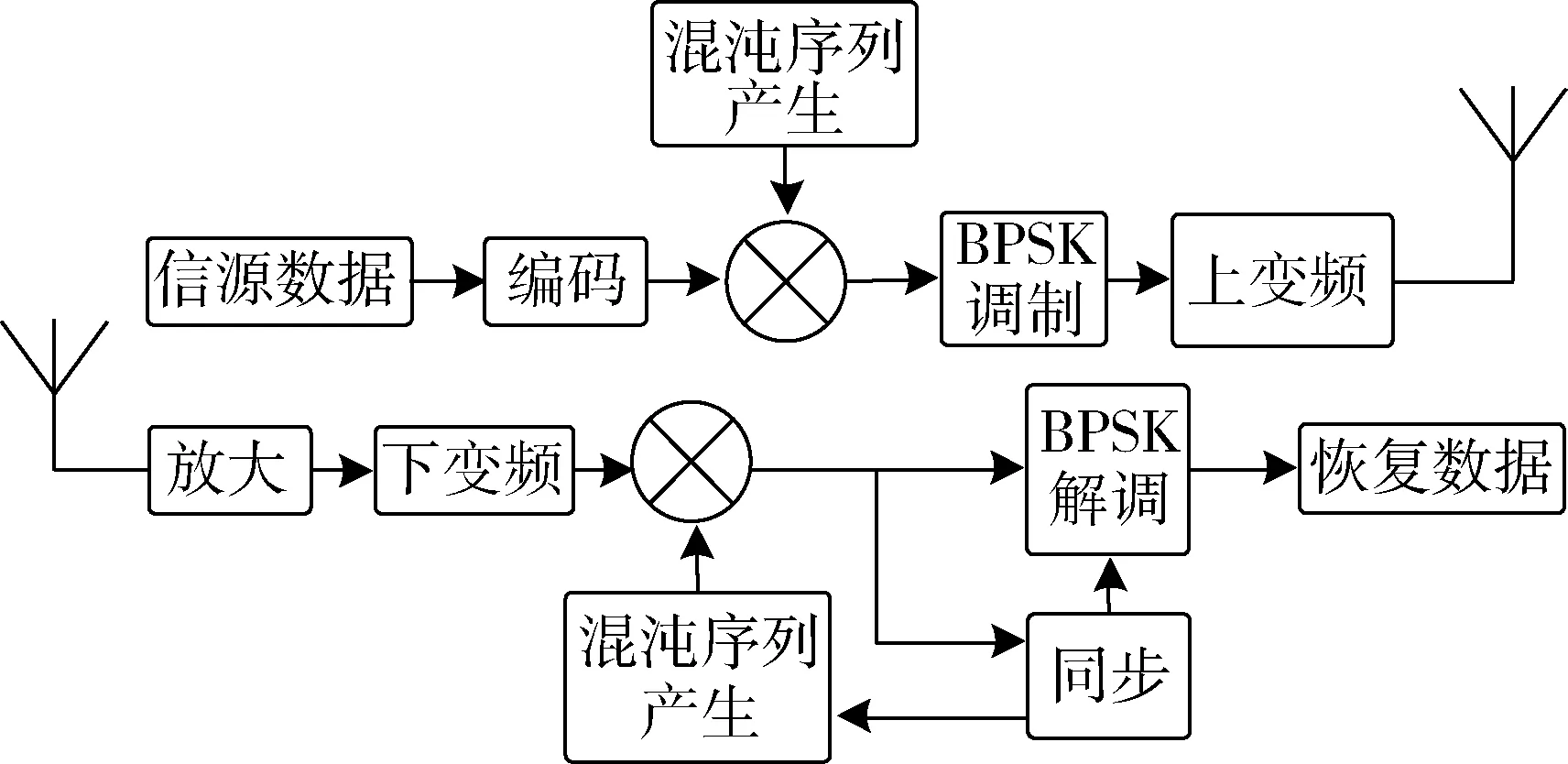
图1 混沌直扩系统框图

混沌扩频通信系统采用混沌序列作为扩频码，充分利用了混沌序列数量众多、伪随机性良好、序列复杂度高等优势，提高了直扩系统的可靠性和安全性。

2 混沌序列的多值量化

混沌序列一般通过非线性混沌映射反复迭代产生，常见的混沌映射有Logistic映射、Chebyshev映射、Tent映射等。本文以Chebyshev混沌映射作为模型进行研究，其映射公式为：

xn+1=f(x)=cos(ωarccosxn)

(1)

初始值x0∈(-1,1)，ω为映射的阶数，当ω=2n时，系统处于混沌状态，其概率密度分布函数为：

(2)

混沌序列应用于扩频通信系统中通常需要经过数值量化处理，相比于常规的二值量化，经过多值量化处理后的序列混沌特性损失减小，序列复杂度更高，伪随机性更强，有利于提升扩频通信系统的性能。下面对混沌序列多值量化的方法进行分析。

假设对混沌序列进行N值量化，则需要通过N+1个划分点将区间 [-1,1] 划分成N段连续的子区间，划分点设为a0,a1，…,aN+1，其中a0=-1,aN+1=1。为了保证N值量化的均匀性，要求混沌序列在每个子区间上的分布概率相同，由式(2)可知Chebyshev混沌映射在子区间[ak,ak+1]上的分布概率为：

(3)

可得

ak=-cos(kπ/N) ,k=0,1,2,…,N

(4)

由于改进型Logistic混沌映射同Chebyshev混沌映射具有相同的概率密度分布函数，因此文中给出的多值量化方法也同样适用于改进型Logistic混沌映射。

3 多值量化混沌序列性能分析

3.1 平衡性

混沌序列的平衡性与载波抑制度有密切的关系，低平衡性的混沌序列会导致直扩系统的载漏增大，将破坏扩频系统保密性、抗干扰和抗侦破的能力。二值量化序列的平衡度E为：

E=|U-V|/L

(5)

式中U与V分别表示混沌序列中1与-1的数目，L表示序列长度。鉴于二值量化平衡度公式不适用于衡量多值量化序列的平衡性，本文采用一种新指标来替代E对多值量化序列的平衡性进行衡量。对于多值量化序列，定义其平衡指数：

rn=|un-1/N|

(6)

定义最大平衡指数：

rmax=|umax-1/N|max

(7)

式中1/N代表多值量化混沌序列中每种量化值应占的理想比例，un代表一种量化值在整个扩频序列中所占的百分比。最大平衡指数表征了整个序列平衡性的最大差异，最大平衡指数越接近零，代表序列的整体平衡性能越好，下面通过仿真对二值量化序列和多值量化的最大平衡指数进行分析。仿真条件：N=4，对混沌序列进行四值量化，量化值设为±1、±2，观察最大平衡指数随着序列长度增加的变化趋势，仿真结果如图2所示。从图中可以看出两种量化方法均具有良好的平衡性，当序列长度大于1 000时，最大平衡指数的数值曲线趋于平稳并接近于零，这证明了本文采用的量化方法是可行的，可以确保多值量化序列拥有良好的平衡性。

图2 最大平衡指数对比

3.2 相关性

相关性是衡量扩频序列性能的重要指标，与扩频通信系统的抗干扰能力和抗多址能力密切相关。理想的扩频序列应该具备类似白噪声一样尖锐的自相关函数和处处为零的互相关函数[9]。设{x}和{y}是周期为L的两个混沌序列，则{x}与{y}的互相关函数Rxy(m)定义为：

(8)

m为两个序列间的相关间隔，定义序列{x}的自相关函数Rx(m)为：

(9)

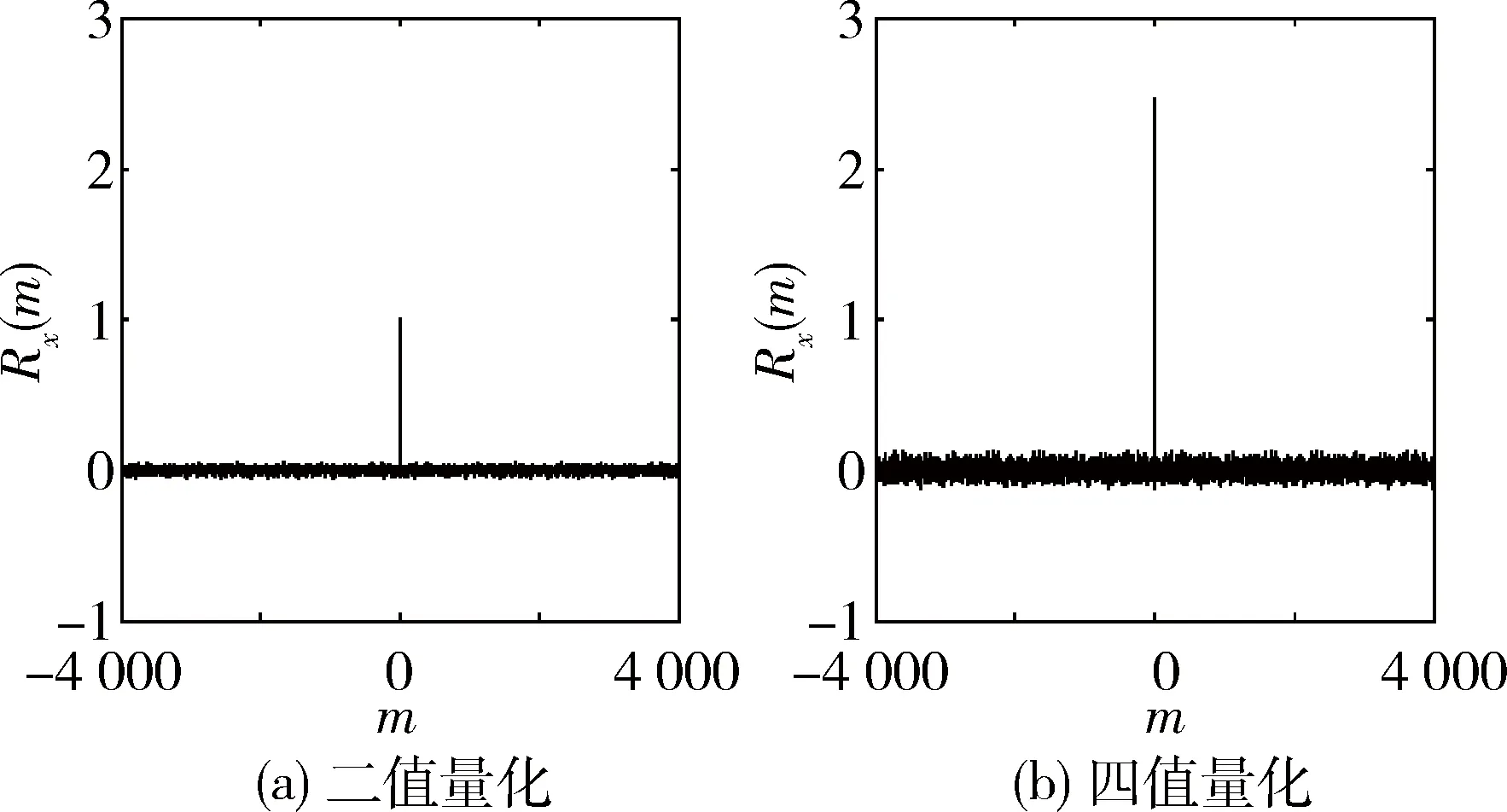
图3 自相关性对比

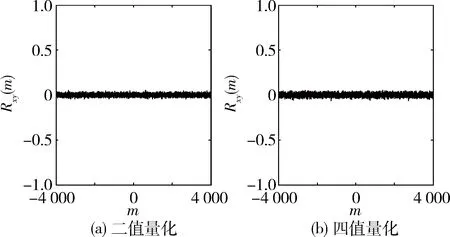
图4 互相关性对比

图3和图4给出了二值量化和多值量化后混沌序列的自相关函数曲线和互相关函数曲线。从图中可以看出多值量化混沌序列相关特性良好，其自相关函数有尖锐的相关峰，互相关函数值非常小，几乎接近于零。同二值量化混沌序列相比多值量化混沌序列的互相关性能差别不大,其自相关函数有更大的相关峰值，有利于合作通信方对扩频信号的检测以及同步过程中对扩频序列的捕获识别。

3.3 误码率性能分析

为了进一步验证多值量化混沌扩频序列的性能，将其作为扩频码应用到直接序列扩频系统中并进行仿真，为保证结果的准确性和可靠性，采用蒙特卡罗方法进行仿真，考虑到平衡性要求，仿真过程中设定混沌扩频序列长度为1 000，默认码元速率为1，调制方式为BPSK，系统信道为高斯白噪声信道(AWGN)，信噪比取值范围是[-20 dB，10 dB]，为了进一步验证多值量化对系统误码率的影响，仿真过程中补充加入八值量化混沌扩频序列进行对比分析，仿真结果如图5所示。

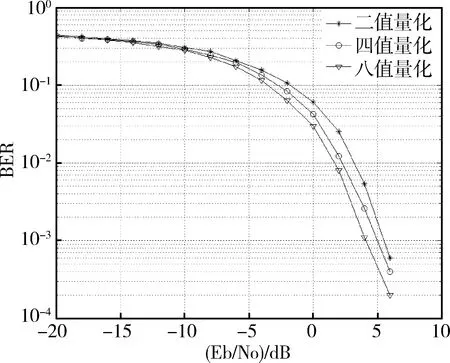
图5 误码率性能对比

从图5中可以看出多值量化序列在AWGN信道下的误码率性能好于二值量化混沌序列，八值量化序列的误码率性能优于四值量化序列，其原因在于多值量化在一定程度上弥补了扩频序列混沌特性的损失，序列的随机性和复杂度均有所提升。仿真结果表明多值量化混沌扩频序列可以有效提高扩频系统的可靠性，降低信号传输的误码率，更适用于扩频通信系统。

3.4 抗截获性能分析

抗截获性能是衡量通信系统可靠性、安全性的重要指标。本文从低检测概率(LPD)和低利用概率(LPE)两个角度对多值量化混沌扩频序列的抗截获性能进行分析。

直扩通信的LPD性能指的是直扩信号被非合作方截获接收机发现的性能。对于一组扩频序列{xn}定义:

(10)

(11)

对于同步相干截获接收机[10],其检测概率为:

(12)

式中γ是截获接收机接收端扩频信号的信噪比，L是截获接收机一次观察的切普数，PFA为虚警概率。仿真参数设定PFA=0.01，L=1 000。多值量化序列的检测概率PD随γ的变化情况如图6所示。

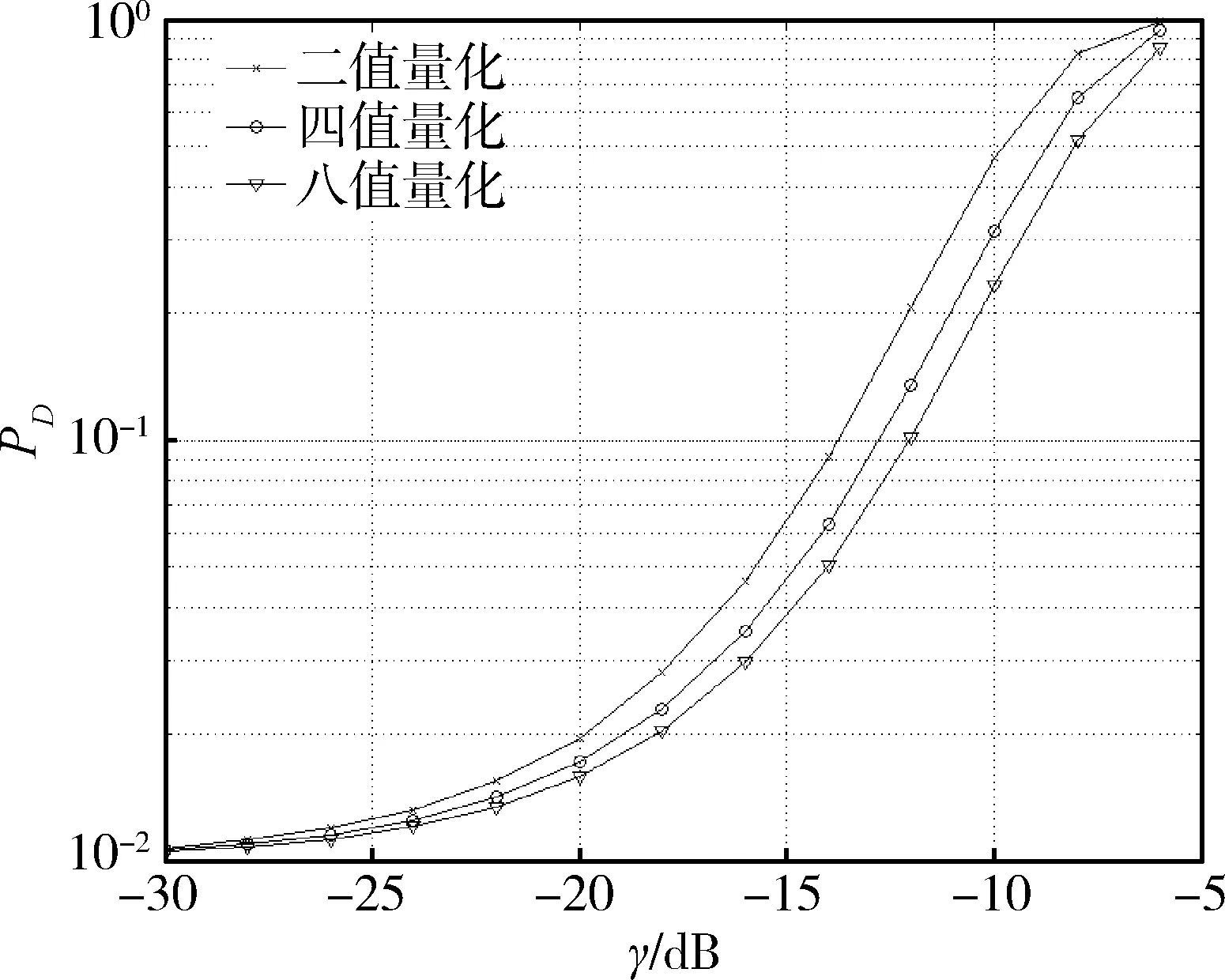
图6 检测概率对比

图7 抗截获误码率对比

从图6中可以看出经过八值量化的扩频信号的检测概率最低，四值量化次之，二值量化扩频信号的检测概率最高。仿真结果表明多值量化混沌序列可以降低扩频信号的检测概率，提高系统的LPD性能。

直扩通信的LPE性能指的是直扩信号被敌方接收机截获后，其携带的信息和情报被还原和获取的能力。相对于二值量化混沌序列，多值量化混沌序列的系统动力学特性更加复杂,系统的参数变量更多，即使敌方接收机检测到我方扩频信号，甚至分析出扩频序列码长、码元速率等系统参数，在不清楚我方混沌扩频序列多值量化规则的情况下也难以对信号携带的信息情报进行还原。敌方在检测到我方直扩信号后经过常规二值相关解扩得到的误码率仿真曲线如图7所示。

从图7中可以看出经过四值量化混沌扩频序列调制过的信号误码率失真严重，经过八值量化混沌扩频序列调制的信号几乎完全失真。仿真结果表明经过多值量化后的混沌扩频序列LPE性能更好，有利于提高通信系统的可靠性和安全性。

4 结论

本文研究了对混沌序列进行多值量化的方法，分析了多值量化混沌扩频序列的平衡性、相关性等性能，并将其作为扩频码应用到直接序列扩频通信系统中进行仿真，仿真结果表明多值量化扩频序列拥有良好的平衡性和相关性，经过多值量化序列调制后的信号在AWGN信道中可获得更好的误码率性能，抗截获性能也有所提高，基于多值量化的混沌扩频序列更适用于扩频通信系统。

[1] 刘嘉兴，何世彪.混沌测控的概念、特性与实现[J].飞行器测控学报，2011，30(1):1-5.

[2] 俞斌，贾雅琼.一种新的混沌扩频序列及其性能分析[J].电子技术应用，2014,39(1)：136-137.

[3] 杜秀丽，甄旭亮，陈波.基于混沌复合序列的直扩系统及其性能分析[J].计算机仿真,2013,30(11):173-176.

[4] 黄展，陈晓萍，赵卫东.截短混沌扩频序列的优选与性能分析[J].电讯技术，2011,51(2):11-15.

[5] VOLOS C, KYPRIANIDIS I M, STOUBOLOS I N. Motion control of robots using a chaotic truly random bits generator[J].Journal of Engineering Science and Technology Review,2012,5(2):6-11.

[6] 张晓蓉，吴成茂.基于混沌与自编码相关融合扩频码的构造[J].电讯技术，2014,54(6):769-773.

[7] 廉晨，达新宇，张亚普.一种新型混沌扩频卫星隐蔽通信算法[J].计算机科学，2014,41(11)：158-161.

[8] 易新兵，杨凯.复合混沌码的直扩系统优化及抗干性能研究[J].计算机工程与设计,2012,33(10):3716-3719.

[9] 余振标，冯久超.一种混沌扩频序列的产生方法及其优选算法[J].物理学报，2008,57(03):1409-1415.

[10] Yu Jin, Yao Yudong. Detection performance of chaotic spreading LPI waveforms[J]. IEEE Transaction on Wireless Communications,2005,4(2):390-396.

Performance analysis of chaotic spread spectrum based on multilevel quantification

Yu Yiding, Wang Yongchuan, Wang Changlong

(Unmanned Aerial System Engineering Department, Ordnance Engineering College, Shijiazhuang 050003,China)

In order to analyse the performance of chaotic spread spectrum sequence based on multilevel quantification, taking the Chebyshev map chaotic sequence for example, a method of multilevel quantification is proposed based on the characteristics of the probability density distribution function of chaotic map. The balance and correlation performance of multilevel quantification spread spectrum sequence is analyzed, the BER of traditional binary sequence and multilevel quantification sequence are simulated in the presence of AWGN channel, and then the anti-interception capability of multilevel quantification sequence is analyzed from two aspects of LPD and LPE. The results show that the multilevel quantification spread spectrum sequence has better BER performance, and the capability of anti-interception is also improved.

chaotic sequences; multilevel quantification; anti-interception

装备预研基金项目(9140A25031314JB34004)

TN914

A

10.19358/j.issn.1674- 7720.2017.06.018

于一丁,王永川,王长龙. 基于多值量化的混沌扩频序列及其性能分析[J].微型机与应用，2017,36(6)：58-61.

2016-10-27)

于一丁(1992-)，通信作者，男，硕士研究生，主要研究方向：测控与信息传输技术。E-mail:yydjxxy@163.com。

王永川(1977-)，男, 副教授，主要研究方向：测控与信息传输技术。

王长龙(1965-)，男，教授，主要研究方向：测控与信息传输技术。