非线性差分方程周期解与次调和解的存在性
2017-04-13范瑶颖
范瑶颖
(广州大学 数学与信息科学学院,广东 广州 510006)
非线性差分方程周期解与次调和解的存在性
范瑶颖
(广州大学 数学与信息科学学院,广东 广州 510006)
本文首先建立二阶差分方程的变分泛函,然后将周期解的存在性转化为相应变分泛函的临界点的存在性,再利用临界点理论中的环绕定理得到该泛函临界点的存在性,证明方程至少有两个非平凡周期解的存在性. 本文结果推广了陈等2008年所得的相关结论.
差分方程;周期解;存在性;环绕定理
1 引言及主要结果
非线性差分方程理论已广泛应用于研究生态学、金融学等学科中出现的离散模型. 差分方程是微分方程离散化,在过去几十年里,许多学者运用上下解理论、不动点理论等经典方法,证明差分方程周期解的存在性、边值问题等,获得了丰富的结果[1-3].
另一方面,已有许多学者对差分方程周期解的存在性与多重性运用不同的方法进行深入广泛的研究,这些方法主要有临界点理论(包括极小极大理论、几何指标理论与Morse理论)、重合度理论等[4-8]. 在这些方法中,临界点理论已成为处理这类问题的强有力的工具.
为方便起见,本文分别记ℕ、ℤ、ℝ为自然数集、整数集、实数集. 对于任意的整数a和b,记ℤ(a)={a, a+1,…};当a≤b时,记ℤ(a, b)={a, a+1,…,b}. *表示向量的转置. 对于任意的n∈ℤ,定义Δu(n)=u(n+1)-u(n),其中Δ为向前差分算子.
本文讨论差分方程周期解的存在性与多重性,其中f∈C(ℤ×ℝ, ℝ),假设(1)是正整数T-周期解函数,有f(t+T,z)=f(t, z),f(t, z)=∇zF(t, z),其中∇zF(t, z)表示F(t, z)关于z的梯度;当p为正整数时,对于任意的n∈ℤ(0,pT),q(n-1)>0且q(n-1)=q(n -1+T),q(0)=q(pT). 考虑f(t, z)在零点与无穷远点处满足超线性增长条件,0<s<1且当δ满足适当条件时,得到方程非平凡周期解的存在性与多重性的若干结果. 本文研究方程(1)的pT-周期解的存在性,通常这样的周期解称为方程的次调和解.

下面我们介绍通过临界点理论研究方程(1)特殊情形的周期解与次调和解的存在性与多重性的相关结论.
当q(n-1)=1,δ=0时,文献[9]运用临界点理论研究方程的特殊形式
周期解与次调和解的存在性与多重性. 其中ℤ是整数集,f(n, x)关于x连续且是超线性的,关于n是周期的,证明方程(2)至少存在两个非平凡的周期解.
当q(n-1)=1时,文献[10]讨论方程的特殊形式

周期解与次调和解的存在性与多重性.
出于以上考虑,本文的目的是利用临界点理论中的环绕定理研究二阶非线性差分方程(1)周期解与次调和解的存在性与多重性.
本文是在文献[10]的基础上,将q(n-1)=1推广至q:(0,pT)→(0,+∞),同样在超线性条件下,进一步对条件优化,例如本文中的条件H2)H3)相比较文献[10]定理1中的条件a2)a3),条件更简化,使用范围更广.
令矩阵A为:

直接验证可知,A是半正定矩阵,并且除0外,A的其他特征值都大于0. 设定A的特征值为
我们的主要结论是:
定理1 假设f与F,δ满足如下条件:
H1) f(t, z)∈C(ℤ×ℝ, ℝ)并且存在正整数p,T,有f(t+T,z)=f(t, z)且f(t, z)=∇zF (t, z),当z≠0时,F(t, z)>0;对于任意的n∈ℤ(0,pT),q(n-1)>0且q(n-1)=q(n -1+T);
H2),对于一切的t∈ℤ一致成立;
H3) 任意的z∈ℝ,存在常数b1>0,b2>0及β>2,使得
H4) 对于任意给定的常数ρ>0,0<s<1使得,其中为矩阵A的最小正特征值;则对于任意给定的正整数p,方程(1)至少存在两个非平凡的以pT为周期的周期解.
注1 由H2),H3)知,f在零点和无穷远点处是超线性增长,或者说F在零点和无穷远点处是超二次增长.
推论1 假设F满足的条件H2),H3)改写为条件H5),H6):
H5) 当z→0时,F(t, z)=o(z2);
H6) 存在常数R1>0,α>2,使得对任意,zf(t, z)≥αF(t, z)>0;则对于任意给定的正整数p,方程(1)至少存在两个非平凡的以pT为周期的周期解.
由条件H2)及f(t, z)的连续性知,对于任意的t∈ℝ,f(t,0)=0,则{u(n)}=0,即u(n)=0(n∈ℤ)也是方程(1)的一个解. 因此存在如下推论:
推论2 假设f与F,δ满足H1)~H4),方程(1)至少存在3个以pT为周期的周期解.
2 变分结构
为了应用临界点理论,首先介绍一些记号和准备知识,并引进适当的变分框架.

考虑定义在X上的泛函


则u是J在X上的临界点(即J′(u)=0)当且仅当

上式正是方程(1). 因此,将(1)周期解的存在性转化为泛函J在X上的临界点的存在性. 或者说,泛函J正是方程(1)的变分泛函. 为方便起见,将u∈X与u=(u(1),u(2),…,u(pT))*看作一致.
当pT>2时,其中u=(u(1),u(2),…,u(pT))*,我们可以将J改写为

注2 pT=1的情形是平凡的;当pT=2时,A具有不同的形式,即:

尽管如此,在这种特殊情形下,论证的结果无需作任何改变. 很明显,0是A的一个特征值,而对应于特征值0的特征向量η0=(1,1,…,1)*,记Z={(v, v,…,v)*∈X v∈ℝ},则Z是X的不变子空间. 记

直接验证可知,ApT-1是正定矩阵,并且rank(A)=rank(ApT-1)=p T- 1. 进而,A是半正定矩阵,并且除0外,A的其他特征值都大于0. 设定A的特征值为0=λ0<λ1≤λ2≤λ3≤…≤λpT-1,对应于特征值λ1, λ2, λ3,…,λpT-1,存在特征向量η1,η2,η3,…,ηpT-1∈X ,使得Aηj=λjηj(j=1,2,…,p T- 1),并且

下面介绍几个定义与引理:

对任意γ>1,在X上定义另外一种函数:


定义1 设X是Banach空间,如果对任何点列{u(n)}⊂X,{J(u)}有界,且当n→∞时蕴含{u(n)}有收敛的子序列,称J∈C1(X,ℝ)满足Palais-Smale条件(简称(PS)条件).
J1) 存在常数σ>0和ρ>0,使得
J2) 存在e∈∂B1∩X2,及常数R2>ρ,使得,并且

则J存在临界值c≥σ,其中

并且

B1表示以θ为中心,以1为半径的开球,∂B1为其边界.
3 主要结论与证明
为证明主要结论,先证明如下引理:
引理3 若f,F满足条件H1),H3),H4),则泛函J在X上满足(PS)条件.
证明 因为J∈C1(X,ℝ),设{u(k)}是X中的(PS)序列,即J(u(k))有界,且当k→∞时,J′(u(k))→0.
由于X是有限维的,故要证明泛函J在X上满足(PS)条件,只需证明:{u(k)}是有界的.
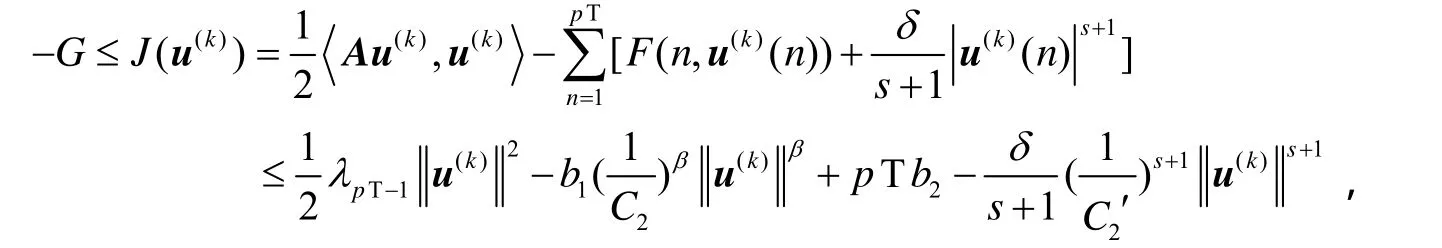
即
由于β>2,δ≥0,0<s<1,b1,b2,C2,C2′,G>0,可知有界. 所以有的子序列在X上收敛,即可得:J满足(PS)条件.
下面将运用环绕定理证明泛函J临界点的存在性.
定理1的证明 由H2)可知,取,存在任意正常数ρ>0,当时,都有



即

由(H4)可知,其中,λ1为矩阵A的最小正特征值,故

其中

所以(J1)成立.
令u=v+re,取e∈∂B1∩Y,对任意v∈Z,以及r∈ℝ,根据条件H3)、式(5)有

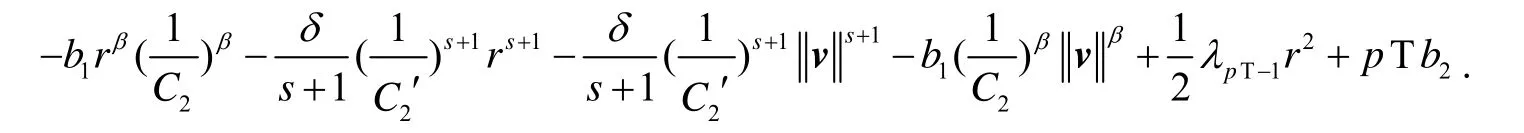
由于β>2,δ≥0,0<s<1,b1,b2,C2,C2′>0,当r→+∞时,J(v+re)→-∞;即存在某个R2>ρ,使得对任意的u∈∂Q,有,其中,所以(J2)成立.
下证c0>0,由式(8)证明可知,任意的u∈Y,n∈ℤ(1,pT),当时,都有
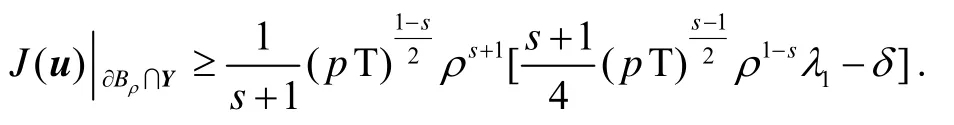
由H4)可知,其中为矩阵A的最小正特征值,所以存在u∈X,使,即由上述证明知是泛函J对应于临界值c的临界点. 假设,则J(u)存在两个不同的临界点,故定理1证明成立. 假设,则,即


以上讨论表明,如果c<c0,方程(1)至少存在两个非平凡的以pT为周期的周期解;如果c=c0,则方程(1)将存在无穷多个非平凡的以pT为周期的周期解. 综上所述,定理1成立.例 对任意给定的常数ρ>0,考虑如下方程


即H2)成立. 取b1=φ(t)+M>0,b2=2>0,β=β1+2>2,显然

即意味着H3)成立. 当q(n-1)≡1时,矩阵A为:


即H4)也满足.
综上,由定理1可知,对于任意给定的正整数p,方程(9)至少存在两个非平凡的以pT为周期的周期解.
[1] AGARWAL R P, WONG F H. Upper and lower solutions method for higher-order discrete boundary values problems [J]. Math Ineq Appl, 1998, 1(4): 551-557.
[2] AGARWAL R P, O’REGAND D, WONG P J Y. Singular discrete(n, p)boundary value problems [J]. Appl Math Lett, 1999, 12(8): 113-119.
[3] ZHOU Zhan, YU Jianshe, CHEN Yuming. Periodic solutions of 2nth-order nonlinear difference equation [J]. Sci China Math, 2010, 53(1): 41-50.
[4] 张恭庆. 临界点理论及其应用[M]. 上海:上海科学技术出版社,1986.
[5] CHANG K C. Infinite dimensional morse theory and multiple somtion problems [M]. New York: Springer-Verlag, 1989.
[6] HALE J K, MAWHIN J. Coincidence degree and periodic solutions of neutral equations [J]. J Differential Equations, 1974, 15: 295-307.
[7] LIU Jiaquan, WANG Zhiqiang. Remarks on subharmonics with minimal periods of Hamiltonian systems [J]. Nonlinear Analysis Theory Methods & Applications, 1993, 20(7): 803-821.
[8] RABINOWITZ P H. Minimax methods in critical point theory with applications to differential equations [J]. CBMS AMS, 1986, 65: 7-18.
[9] 郭志明,庾建设. 二阶超线性差分方程周期解与次调和解的存在性[J]. 中国科学,2003, 33(3): 226-235.
[10] 陈永刚,胡哲. 非线性二阶差分方程周期解的多重性[J]. 甘肃科学学报,2008, 20(2): 13-17.
[责任编辑:韦韬]
Existence of Periodic and Subharmonic Solutions for Nonlinear Difference Equations
FAN Yao-ying
(School of Mathematics and Information Science, Guangzhou University, Guangzhou 510006, China)
In this paper, we study second-order suplinear difference equations. First, by establishing a suitable variational framework, we turn the periodic solution problem into a critical point problem of corresponding functional. Next, by using the Linking Theorem of critical point theory, we obtain the existence of a critical point of the functional and prove the existence of at least two nontrivial periodic solutions. The results generalize Chen’s related conclusion reached in 2008.
difference equations; periodic solutions; existence; linking theorem
O175.7
A
1006-7302(2017)01-0007-07
2016-11-08
范瑶颖(1990—),女,广东汕头人,在读硕士生,研究方向为常微分方程理论及应用.
