基于ANSYS和强度折减法的边坡稳定性分析
2017-04-13孙增春
孙增春
(重庆交通大学 河海学院,重庆 400074)
基于ANSYS和强度折减法的边坡稳定性分析
孙增春
(重庆交通大学 河海学院,重庆 400074)
探讨了强度折减法的基本原理、安全系数、屈服准则和破坏标准等内容,结合ANSYS有限元软件,对水泥库边坡工程在不同破坏标准下的稳定性进行对比分析. 计算过程中,随着折减系数的不断改变,会得到不同的黏聚力和内摩擦角参数值,再将其输入到ANSYS中的等面积D-P本构方程中计算至不收敛,发现边坡的安全系数与此时的折减系数是相等的. 结果表明:采用塑性区贯通和位移的突变作为边坡破坏标准所得到的安全系数与传统方法计算得到的安全系数十分接近,从而表明有限元强度折减法在边坡稳定性分析中具有可行性.
ANSYS;强度折减法;边坡稳定;安全系数
边坡稳定性是基础设施建设过程中不可避免的问题,一旦出现边坡失稳的状况往往带来极大的人员伤亡和财产损失. 因此,对边坡工程进行稳定性分析和评价是十分重要的. 多年来,许多专家学者致力于边坡稳定性的研究,取得了巨大的成果,但仍存在一些问题需要解决. 极限平衡法是使用最早、应用最广的一种定量分析方法,常见方法有瑞典条分法、Janbu条分法、Spencer法和传递系数法等. 由于极限平衡法不考虑土体破坏前的变形过程和变形量,只关心岩土体处于最后整体滑动时的状态及条件,在求解安全系数时必须提前对一些影响因素进行假定,如滑裂面的假定、土条条分假定等,从而导致其应用范围受到了一定的限制[1-3]. 自20世纪七八十年代以来,计算机及计算技术手段迅速发展,推动了非线性弹塑性力学和数值计算方法的发展. 其中,数值分析方法考虑了土体的应力应变关系,不需要进行条间力的简化和事前确定滑裂面的形状和位置,能够反映岩土体真实的受力状态,常用方法有有限元法、离散单元法、拉格朗日法等[4-5].
本文在强度折减法的基础上,通过对ANSYS数值模拟软件中屈服准则的改进,研究了不同判断标准下边坡的稳定性,并与Janbu条分法和折线滑动面传递系数法计算所得结果进行对比分析.
1 强度折减法的理论基础
1.1 强度折减法的计算原理
抗剪强度折减系数指当外部所施加的荷载处于恒定状态时,土体内部所发挥的最大抗剪强度与外荷载作用时内部产生的实际剪应力的比值. 在这一概念的基础上对边坡土体进行有限元数值分析,对于边坡内的某一点来说,根据极限平衡法中对安全系数的定义,还应将该点的抗剪强度考虑在内,即:
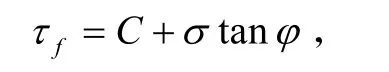
式中,τf为土体的抗剪强度;C为土体的粘聚力;σ为作用在土体上的正应力;φ为内摩擦角. 则该点土体的安全系数:

式中,F为安全系数;τ为土体的剪应力.
如果此时边坡内部的土体没有出现破坏现象,则真实存在于土体内部的剪应力与真正发挥出来的抗剪强度是相等的,即:

折减后的强度指标可表示为:
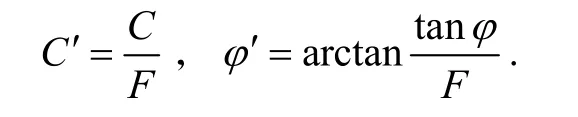
通过对土体的剪切强度进行不断的折减,使边坡从稳定状态逐渐向破坏状态转变,找到边坡岩土体最容易发生破坏的区域,进而找出对边坡进行防护与加固的可靠措施.
1.2 ANSYS中屈服准则的实现
岩土体的屈服准则有许多种,本文主要针对目前在有限元分析中最为常用的D-P屈服准则进行分析[6]. D-P屈服准则在M-C屈服准则的基础上根据不同的光滑面变化出下面4种情况:

图1 屈服准则在π平面上的曲线
1)D-P1,外角点外接D-P圆:

2)D-P2,内角点外接D-P圆:

3)D-P3,等面积D-P圆:

4)D-P4,内切D-P圆:

由于ANSYS只提供了外角点外接D-P圆模型,而等面积D-P圆模型是边坡稳定性分析时用得最多的,本文给出了二者之间具体的换算过程. 因:

所以,等面积D-P圆屈服准则所需要的φ′和C′:

1.3 边坡失稳的判断标准
目前,普遍认可的边坡失稳的判断标准有3种:1)计算的收敛性. 在利用有限元软件求解过程中,可以通过设定迭代的次数、假定节点不平衡力和外荷载的比值、力和位移的收敛标准值等来作为边坡破坏的判断依据;2)塑性区贯通. 根据某一幅值的广义塑性应变或等效塑性应变自坡脚下方向坡顶上方是否贯通作为边坡破坏的标志;3)位移的突变. 边坡的破坏常常伴随着位移的较大变化,因此可以根据计算区域内某一部位或点的位移是否发生突变作为判断依据.
对于上述三种判断标准目前仍存在很大的争议. 郑颖人等[7-8]认为把计算的收敛性作为判断依据是比较合理的,而且计算结果更符合实际情况;栾茂田等[9]比较认可将塑性区是否发生贯通作为边坡失稳的判断依据;李红等[10]更加倾向于把位移的突变作为边坡失稳的判断标准;裴利剑等[11]认为三种判断标准都存在合理的地方,在理论上是不矛盾的,误差的出现只不过是人为或数值计算导致的.
总之,三种判断标准都具有一定的局限性. 因此,本文选取塑性区贯通和位移的突变两个标准作为边坡失稳的判断标准进行分析.

图2 结构典型剖面图(单位:m)
2 工程实例
2.1 边坡结构
图2所示为东方希望重庆水泥有限公司水泥库边坡工程典型剖面及主要土层. 工程位于东方希望重庆水泥有限公司已建码头后方,后接厂区水泥库,长约140 m. 原岸坡为原河岸岸坡和近年厂区建设弃土石堆积而成,最高处约35 m.根据该区域地质灾害危险性评估和现场情况,决定对该岸坡进行治理. 在设计加固方案前需要对原有边坡进行稳定性计算. 由于强度折减法的原理是不断降低岩土体的强度参数,所以水的作用造成的材料强度的降低已考虑在内,无需单独考虑. 该工程边坡数值模拟计算参数如表1所示.

表1 数值模拟计算参数
2.2 有限元计算模型
在ANSYS中按照平面应变问题建立模型. 计算单元选取适合于弹塑性分析的PLANE82八节点等参单元,材料的应力应变关系为等面积D-P圆模型. 网格划分后模型节点数有8 449个,单元数有2 730个,有限元模型网格如图3所示.

图3 有限元网格划分
2.3 计算结果及分析
在计算过程中,通过不断改变折减系数F的大小能够得到不同的φ′、C′值,将其输入到ANSYA的等面积D-P本构方程中,分析在折减系数不同的情况下边坡的破坏状态.
图4表示的是不同折减系数下边坡的塑性应变云图. 从图4可以清晰地看出:随着强度折减系数的增大,边坡塑性区的分布也在不断发生变化,即在回填土与中风化层的界面处首先出现了塑性区,随着折减系数F的增加,塑性区逐渐向坡脚和坡顶发展,当F=1.50时边坡内部的塑性区已经扩展到坡脚;F=1.53时,塑性区向上扩展到坡顶,此时紧贴岩层与土层的界面出现了一条完全贯通的塑性带,这预示着边坡整体失稳,形成了滑动带. 因此,可认为该边坡工程的安全系数为1.53.

图4 不同折减系数下边坡的塑性应变云图
图5表示的是不同折减系数下边坡的水平位移变化图. 从图5可以看出:边坡水平方向的位移随折减系数F的增加发生了很大的变化. 一开始,随着折减系数的增加,水平位移增长的比较缓慢;当折减系数大于1.52时,水平位移剧增,从F=1.52时的0.314 m增长到F=1.53时的0.486 m,表明此时边坡发生了破坏. 因此,可认为此时的边坡安全系数为1.53.

图5 不同折减系数下边坡的水平位移变化图
2.4 不同计算方法的结果对比
为了能够更好地说明有限元强度折减法所获得的安全系数的准确性,作者还采用Janbu条分法和折线滑动面传递系数法计算了该边坡的安全系数,得到的结果为1.48和1.51,与1.53分别相差3.38%和1.32%. 通过比较可以看出,传统方法计算获得的安全系数与有限元强度折减法获得的安全系数相差不大,且在误差允许的范围内,但传统方法计算得到的结果偏于保守,这是由于强度折减法不用事先假定滑裂面的形状和位置,并且充分考虑了土体内部的应力—应变关系. 所以,通过有限元强度折减法获得的安全系数更加合理,能够更好满足工程经济性和安全性的要求.
3 结论
1)强度折减法分析边坡稳定性时,不需要像传统计算方法一样事先假定边坡的滑裂面. 边坡的变形特性、塑性区形成都是由实际应力应变状态“自然”形成的.
2)将塑性区贯通和特征点的位移突变作为边坡破坏的判断标准计算得到的结果基本上是一致的,表明这两种判断标准具有可行性,在今后的实际应用中可以将二者结合起来使用.
3)采用强度折减法能够直观真实地反映边坡坡体的整体和局部破坏状态,得到的安全系数更加合理可靠,在实际工程中有较好的应用前景.
[1] 陈祖煜. 边坡稳定性分析—原理·方法·程序[M]. 北京:中国水利水电出版社,2005.
[2] 董志怡,陈从新,徐健,等. 边坡稳定性分析的条块稳定系数法[J]. 岩土力学,2009, 30(5): 1394-1398.
[3] 朱大勇. 边坡临界滑动场及其数值模拟[J]. 岩土工程学报,1997, 19(1): 63-68.
[4] 郑颖人. 岩土数值极限分析方法的发展与应用[J]. 岩石力学与工程学报,2012, 31(7): 1297-1316.
[5] 郑宏,李春光,李焯芬,等. 求解安全系数的有限元法[J]. 岩土工程学报,2002, 24(5): 626-628.
[6] 邓楚键,何国杰,郑颖人. 基于M-C准则的D-P系列准则在岩土工程中的应用研究[J]. 岩土工程学报,2008, 26(6): 735-739.
[7] 郑颖人,赵尚毅,邓楚键,等. 有限元极限分析法发展及其在岩土工程中的应用[J]. 中国工程科学,2006, 8(12): 39-61.
[8] 赵尚毅,郑颖人,时卫民,等. 用有限元强度折减法求边坡稳定安全系数[J]. 岩土工程学报,2002, 24(3): 343-346.
[9] 栾茂田,武亚军,年延凯. 强度折减有限元法中边坡失稳的塑性区判据及其应用[J]. 防灾减灾工程学报,2003, 23(3): 1-8.
[10] 李红,宫必宁,陈琰,等. 有限元强度折减法边坡失稳判据[J]. 水利与建筑工程学报,2007, 5(1): 79-82.
[11] 裴利剑,屈本宁,钱闪. 有限元强度折减法边坡失稳判据的统一性[J]. 岩土力学,2010, 31(10): 3337-3341.
[责任编辑:熊玉涛]
Slope Stability Analysis Based on ANSYS and the Strength Reduction Method
SUN Zeng-chun
(College of River and Ocean Engineering, Chongqing Jiaotong University, Chongqing 400074)
This paper discusses the basic principle, safety coefficients, yield criteria and failure criteria of the strength reduction method, and in combination with the ANSYS finite element software, makes a comparative analysis of the stability of slope engineering of cement bunkers under different failure criteria. In the process of calculation, with the continuous change of reduction coefficients, different parameter values of cohesion and internal friction angle were obtained, which were then put into the homalographic D-P constitutive equation of the ANSYS to calculate the convergence and it was found that the safety coefficient of the slope was equal to the reduction coefficient. The results show that the safety coefficient obtained by using abrupt change of coalescence and displacement in plastic zone as slope failure criteria in the plastic zone is very close to that obtained with the traditional method, which shows that the finite element strength reduction method is feasible in slope stability analysis.
ANSYS; strength reduction method; slop stability; safety coefficients
TU45
A
1006-7302(2017)01-0065-05
2016-10-20
孙增春(1993—),男,山东菏泽人,在读硕士生,研究方向为水工结构、岩土工程.
