图的无符号拉普拉斯谱半径与最大度
2017-04-13邢润丹
邢润丹
(五邑大学 计算机学院,广东 江门 529020)
图的无符号拉普拉斯谱半径与最大度
邢润丹
(五邑大学 计算机学院,广东 江门 529020)
图的无符号拉普拉斯矩阵定义为其度矩阵与邻接矩阵之和,其最大特征值称为图的无符号拉普拉斯谱半径. 本文证明了若连通图G的无符号拉普拉斯谱半径大于那么G中必定含2个最大度点.
无符号拉普拉斯矩阵;无符号拉普拉斯谱半径;最大度
1 图的无符号拉普拉斯谱半径
本文研究简单无向图. 假设连通图G的顶点集为V(G)={v1, v2,…,vn},边集为E(G). 图G的度矩阵D(G)定义为n×n对角矩阵,其中(i, i)元为顶点vi的度dG(vi). G的邻接矩阵定义为n×n矩阵A(G)=(aij),其中当vivj∈E(G)时,aij=1,否则aij=0. 那么,G的无符号拉普拉斯矩阵就定义为Q(G)=D(G)+A(G)[1-2]. 显而易见,Q(G)为对称矩阵,其最大特征值称为图G的无符号拉普拉斯谱半径,记为q(G).
对于任一图G中的顶点u,令NG(u)表示点u在G中的邻点所成之集. 顶点u在图G中的度数,是指集合NG(u)的元素个数,记为dG(u). 记Δ(G)为图G的最大度. 图G中度为Δ(G)的顶点称为图G的最大度点.
拟证明以下结论:
2 图的Q-Perron向量
对于方阵A,若存在置换矩阵P,使得PAPT为一分块上三角矩阵,则称A为可约矩阵;否则称A为不可约矩阵.
若A为n阶方阵,其特征值为λ1, λ2,…,λn,则称ρ(A)=max{|λ1|,|λ2|,…,|λn|}为A的谱半径. 易见ρ(A)不一定是A的特征值.
在引入Q-Perron向量的概念之前,先介绍非负不可约矩阵的一个重要定理.
引理1[3](Perron-Frobenius定理) 假设A为非负不可约方阵,那么以下结论成立:
1)ρ(A)>0;
2)ρ(A)为A的一个特征值;
3)存在一个正向量x,使得Ax=ρ(A) x;
4)ρ(A)是A的单重特征值.
假设G为连通图. 由于矩阵Q(G)为非负不可约矩阵,根据引理1(Perron-Frobenius定理),q(G)>0为Q(G)的单重特征值,且对应q(G)存在唯一单位正特征向量,将其称为图G的Q-Perron向量.
3 图的无符号拉普拉斯谱半径与最大度
以下给出连通图的无符号拉普拉斯谱半径与其最大度的一个结论.
证明:记Δ=Δ(G). 假设图G只含唯一一个最大度点,不妨记为u. 即dG(u)=Δ. 现构造|V(G)|维列向量y,其中
通过计算向量Q(G)y的元素,得
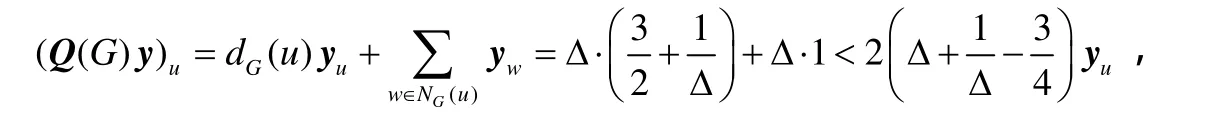
其中最后一个不等式成立是因为

而对于任一v∈V(G){u},有


由于G为连通图,根据引理1,令x为图G的Q-Perron向量. 那么有Q(G)x=q(G)x,且由于x和y均为正向量,有xTy>0. 从而

[1] CVETKOVIC D, ROWLINSON P, SIMIS S Simić. Eigenvalue bounds for the signless Laplacian [J]. Publ Inst Math, 2007, 81(95): 11-27.
[2] WANG Jianfeng, HUANG Qiongxiang, BELARDO F, et al. On graphs whose signless Laplacian index does not exceed 4.5 [J]. Linear Algebra Appl, 2009(431): 162-178.
[3] HORN R A, JOHNSON C R, Matrix analysis[M]. Cambridge: Cambridge University Press, 1990.
[责任编辑:韦 韬]
Signless Laplacian Spectral Radius and Maximum Degree of Graphs
XING Run-dan
(School of Computer Science, Wuyi University, Jiangmen 529020, China)
The signless Laplacian matrix of a graph is defined to be the sum of its degree matrix and its adjacency matrix. The signless Laplacian spectral radius of a graph is the largest eigenvalue of its signless Laplacian matrix. We show that if the signless Laplacian spectral radius of a connected graph G is greater thanthen G contains two vertices of maximum degree.
signless Laplacian matrix; signless Laplacian spectral radius; maximum degree
O157.5;O157.6
A
1006-7302(2017)01-0005-02
2016-08-26
广东省自然科学基金博士科研启动项目(2014A030310413);广东省教育厅省级重大项目(2014KZDXM055);五邑大学青年基金资助项目(2014zk05).
邢润丹(1985—),女,广东揭阳人,讲师,博士,主要从事组合数学与图论的研究.
