基于极端学习机的Demons图像配准

高弘治,闫德勤,杨 伊,刘彩凤

(辽宁师范大学 计算机与信息技术学院,辽宁 大连 116081)

基于极端学习机的Demons图像配准

高弘治,闫德勤,杨 伊,刘彩凤

(辽宁师范大学 计算机与信息技术学院,辽宁 大连 116081)

医学图像配准是医学诊断中的重要研究内容，配准精度和速度也是众多研究的核心。图像配准过程可设想为是一种神经网络的学习过程，基于这种想法，引入极端学习机(ELM)这一系统对图像完成配准。该方法速度快、鲁棒性高，最重要的是它能不依赖梯度信息，从而很好地避开了点周围间的互相干扰，考虑到其学习过程的准确性，引入鲁棒激活函数学习机，以更好地提高配准学习系统的准确度，并提高其稳定性。

图像配准；极端学习机；鲁棒激活函数

0 引言

近年来，随着医学诊断越趋可视化，对于医学图像的研究也越发必要，其中图像配准是医学诊断和引导治疗临床应用的重要研究方向，不断出现的研究成果表明该领域已成为研究热点[1-3]，其研究按照图像形变性质主要分为3个方面，即弹性模型、粘流体模型、微分同胚非线性图像配准。弹性模型[4-5]由Broit首次提出，该模型将源图像到目标图像的形变过程建模为一个弹性形变的物理过程。这个物理过程由内力和外力两种力来控制，当作用于弹性体上的外力和内力达到平衡时形变过程结束。弹性体的形变可以由Navier线性方程来描述。由于弹性变换模型一般适用于组织形变较小的情况，不适用于大形变。近年来，有关学者结合黎曼弹性能量和微分流形的理论把线性弹性模型进行改进以适于非线性弹性形变的配准[6-7]。粘流体模型由Christensen等[8]提出。该模型允许更大程度的形变，特别适合不同个体之间(Inter-subject)包括图谱之间的配准。流体形变可以由Navier-Stokes偏微方程表示。但对于约束较强的组织不太适合，该模型的计算效率不高[9]。微分同胚非线性配准方法中基于Demons[10]系列算法以其深刻的物理和数学模型基础及计算效率优势备受人们关注[3-5]。微分同胚非刚性配准[11]应用代数结构实现静态速度场上微分同胚变换[12]所用到的映射具有光滑可逆性且逆映射也是光滑的。其最大特点是保持图像的拓扑结构在配准前后不发生改变，因此，它对大小形变都适用。但是此系列算法在形变过程中依赖梯度，很容易受到不连续的离群点干扰，而且刚性配准算法在于用线性刚性方程对形变位移正则化。尽管其在计算上是有效的，但是其正则化因子仅仅对小形变是有效的，且对于偏离位移是不持续的。基于Demons模型，较早的有Active Demons[13], 利用对浮动图像和参考的正力和负力互相约束实现配准；目前研究较广泛的有Log Demons[14]基于此思想的改进算法如iLog Demons[15]; Spectral Demons[16]即一种基于图像流形特征图谱的算法；单隐层前馈神经网络(Single-hidden Layer Feed Forward Networks，SLFNs) 基于仿生学思想，模拟生物信息处理方法以数学优化形式实现信息的提取。模型学习能力强，能够很好地逼近复杂的非线性函数，因而广泛应用于分类及预测等问题，目前此领域中研究的热点模型是极端学习机(Extreme Learning Machines-ELM)[17-18]，采用单隐层前馈神经网络(Single-hidden Layer Feedforward Networks，SLFNs)，利用最小平方回归优化计算输出，避免了传统神经网络的迭代计算。由于受到极端学习机的学习模型启发，在神经网络(Neural Network)[19-20]研究中发现，受训样本通过神经网络可以对学习样本进行认知和自我反馈，这恰恰在思想上与配准不谋而合，同样，在医学图像配准中也是将待配准图像对参考图像的学习和自身调节而达到一致的过程，那么可以认为在图像上的灰度点是神经元，通过构造神经网络而实现其向参考图像形变。在实验中，对非线性图像的配准往往要用到图像间的最优相似性测度实施监督，而这也是配准的一个重要准则，而对于临床应用，形变点对点的位移映射必须要用高斯平滑，使之平滑配准，这无形中对图像的原始信息也是一种浪费。为了避免提取图像信息，同时避免过多地依赖梯度运算，提出鲁棒激活函数图像配准学习机。该方法具有很强的鲁棒性，且不过多依赖图像周边信息，利用神经中的学习和记忆实现图像信息最大程度的保留。但是，此方法还在雏形阶段，其中有很多缺点和不足，比如算法容易产生像素点离群和脱离情况，因为是对图像进行训练映射而不是精准函数映射，所以其恢复程度取决于神经网络的健全性，希望这一方法在今后可以逐渐完善。

1 极端学习机图像配准

设M是浮动图像，T是参考图像。在配准中浮动图像向参考图像形变的过程Demons系列最初的能量函数构造如下：

(1)

第一项是对图像像素灰度值的约束，第二项为形变的约束。当能量函数达到最小时，配准过程完毕。根据此最初想法，SpectralDemons[16]方法对能量函数改进如下：

(2)

三项为图谱约束，即在配准过程中要考虑对图像特征图谱最优的形变量。同样LogDemons系列算法的能量函数构造为：

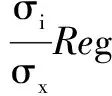
(3)

对比发现，在Log Demons[11]，指数场exp(u)对形变要保持空间的微分同胚性。

本文提出的基于学习模型的Demons算法的能量函数为：

(4)

配准是通过不断的形变迭代求得图像的位移量，在此过程中要考虑每次形变是连续的，并且浮动图像向参考图像学习项约束，故构造第三项的约束条件。

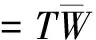
(5)

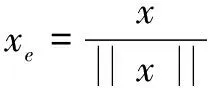
(6)

令隐层像素神经元节点个数为L，上述方程(5)可写成矩阵形式：HW=T，其中形变隐层输出矩阵：

(7)

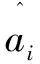
(8)

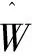
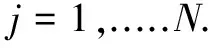
(9)

式(7)的优化模型可通过拉格朗日方法转化为无条件最优化问题进行求解[3]。通过以上求解，可以得出对参考图像的训练模型H和权值矩阵W，进而让浮动图像神经网络对模型进行很好的学习，实现浮动图像与参考图像配准。

fRAF[1]是本文中所用到的鲁棒激活函数，将Gaussian核函数中的欧氏距离转化为Cosined 度量，可以避免离群点对核函数的影响；同时fRAF核具有激活函数的优良性质，不会导致像素点隐层输出矩阵的病态问题，进而能更好地符合图像配准的像素神经元学习过程。

为了更好地保证配准的准确度和稳定性，本文选取fRAF，其良好的鲁棒性使得像素点的离群率大大减小。图1、图2是Lena图像配准实验和脑部医学图像配准实验对激活函数效能的分析，其中横坐标为像素群体比例，纵坐标为学习精度。

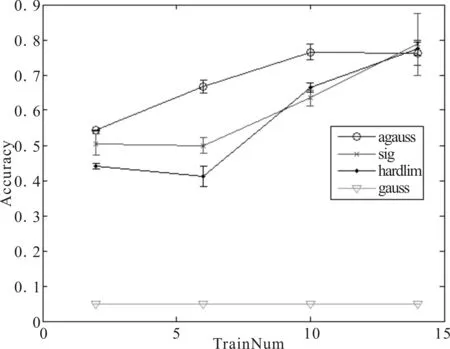
图1 Lena实验中的激活函数精度分析

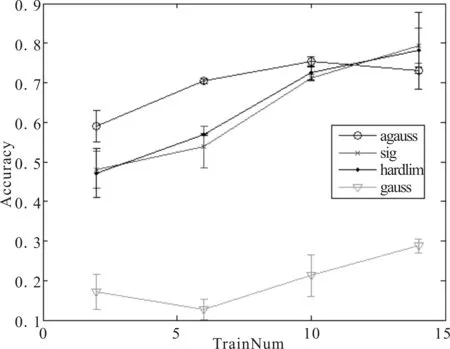
图2 脑部实验中的激活函数精度分析

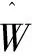
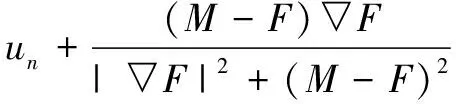
2 实验及结果分析

2.1 实验与分析

第1组实验：利用形变后的Lena图像作为未形变图像(见图3参考图像)与浮动图像(见图4)。不同的配准结果如图5～图8所示。

图3 参考图像 图4浮动图像

图5 本文方法配准后图像 图6 Active Demons配准结果

图7 Log Demons配准结果 图8 Spectral Demons配准结果

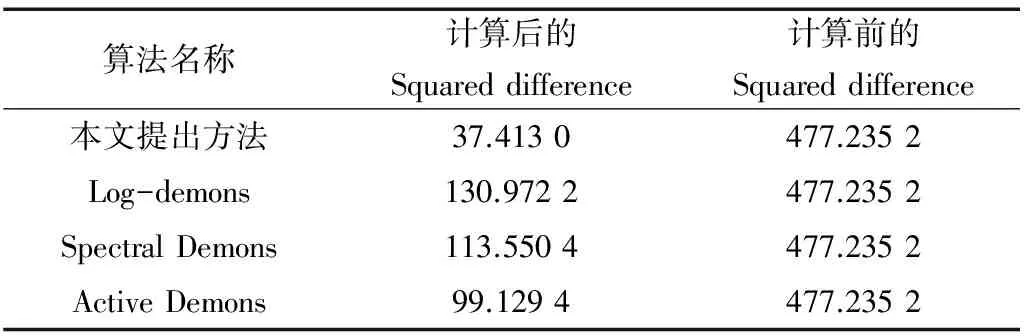
表1 Lena实验各算法SSD测度

第2组脑部实验：实验的参考图像如图9所示，浮动图像如图10所示，不同的配准结果如图11～图14所示。

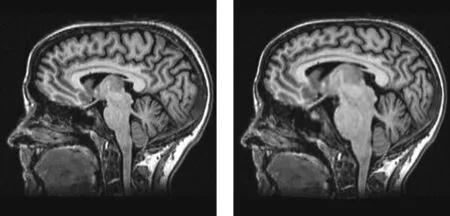
图9 参考图像 图10 浮动图像

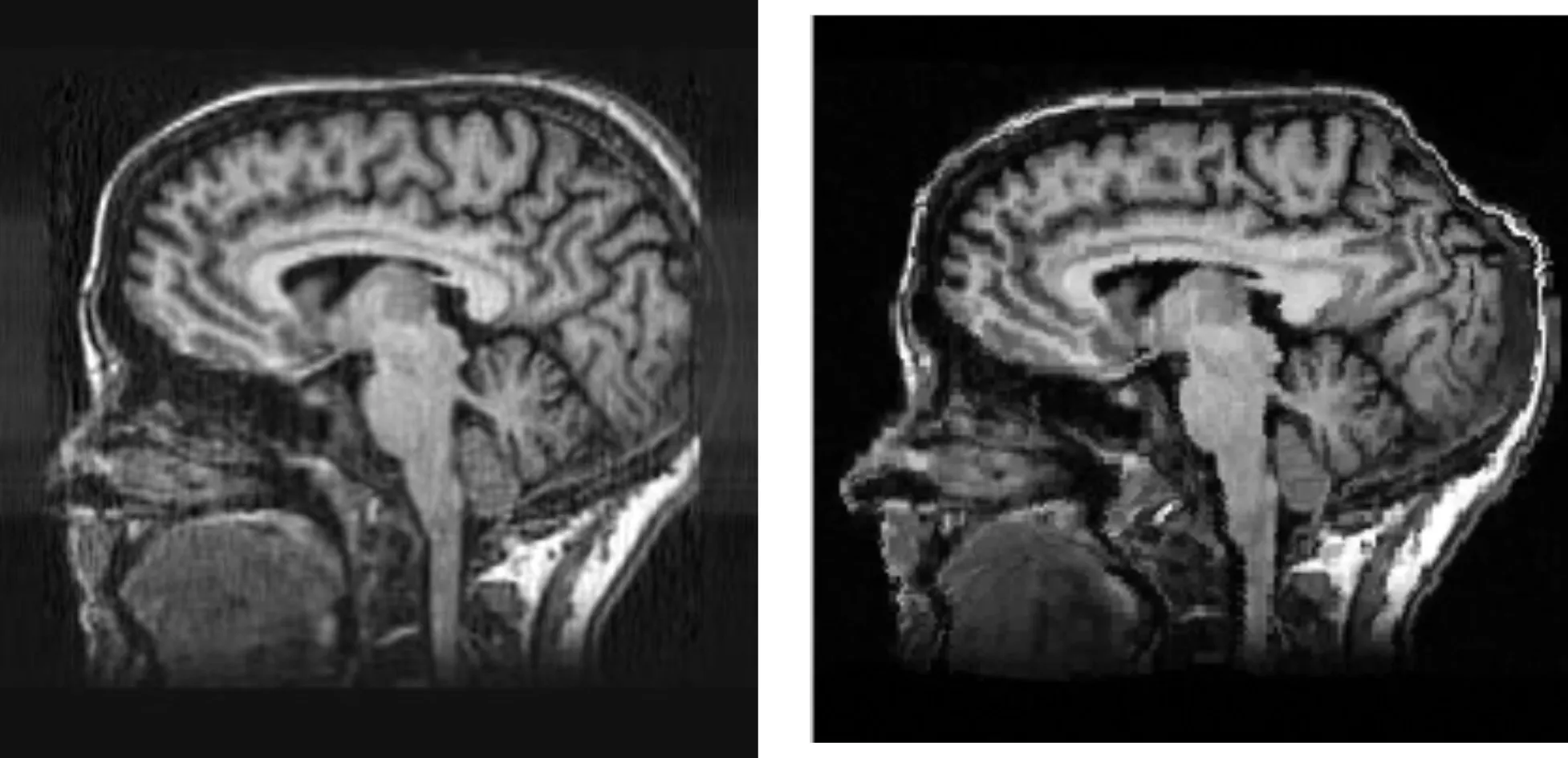
图11 配准图像 图12 Active Demons配准结果

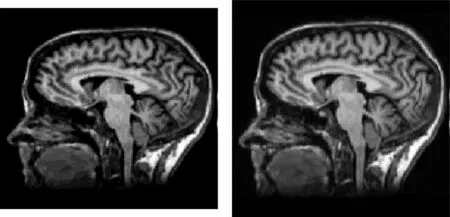
图13 Log Demons配准结果 14 Spectral Demons配准结果

表2 脑部实验各算法SSD测度

算法名称计算后的Squareddifference计算前的Squareddifference本文提出方法22．1579288．6278Log⁃demons149．2658288．6278SpectralDemons124．7426288．6278ActiveDemons69．3579288．6278

2.2 实验结论

从图5中可以看到配准的效果是显而易见的，全局和细节的配准效果都很好，但是实验很大程度上依赖像素神经隐层输入个数，所以选取的参数L为10 000，但是从实验结果还是可以看到配准图像上有离群点产生。图11为本文提出方法对医学脑部图像的图像配准，中部和轮廓配准效果很好，也能看到浮动图像脑中部的结构有病变而产生肥大，配准图像则对浮动图像有很好恢复，但是像素神经在训练过程产生轮廓边缘像素脱离，希望在日后可以对存在的问题进行改进和修复。

[1] S L LIU,L FENG.Robust activation function and its application:semi-superxised kernel extreme learning method[J].Neurocomputing,2014(144):318-328.

[2] P DUPUIS,U GRENANDER.Variational problems on flows of diffeomorphisms for image matching[J]. Quarterly of Applied Mathematics,1998,56(3):587-600.

[3] A SOTIRAS,C DAVATZIKOS.Deformable medical image registration:a survey[J].IEEE Transactions on Medical Imaging,2013,32(7):1153-1190.

[4] C BROIT.Optimal registration of deformed images[D].Philadelphia:University of Pennsylvania,1981.

[5] R BAJSCY,S KOVACIC.Multiresolution elastic matching[J].Computer Vision, Graphics and Image Processing,1989.

[6] X PENNEC,R STEFANESCU.Riemannian elasticity: a statistical regularization framework for non-linear registration[C].In Proc. Medical Image Computing and Computer Assisted Intervention:MICCAI'05,2005：943-950.

[7] J ASHBURNER.A fast dffeomorphic image registration algorithm[J].NeuroImage,2007(38):95-113.

[8] G E CHRISTENSEN,R D RABBITT.Deformable templates using large deformation kinematics[J].IEEE Transactions on Image Processing,1996,5(10):1435-1447.

[9] M C CHIANG.Fluid registration of diffusion tensor images using information theory[J].IEEE Transactions on Medical Imaging,2008,27(4):442-456.

[10] A BRUHN,J WEICERT.Combining the advantages of local and global optical flow methods. International [J].Journal of Computer Vision,2005,61(3):211-231.

[11] T VERCAUTEREN,X PENNEC.Non-parametric diffeomorphic image registration with the demons algorithm[C].In Proc. Medical Image Computing and Computer-Assisted Intervention:MICCAI'07,2007：319-326.

[12] B FISCHER.Curvature based image registration[J].Journal of Mathematical Imaging and Vision,2003(18):81-85.

[13] H WANG.Validation of an accelerated 'demons' algorithm for deformable image registration in radiation therapy[J].Physics in Medicine and Biology,2005,50(12):2887-2905.

[14] X PENNEC,A PERCHANT.Diffeomorphic demons:efficient non-parametric image registration[J]. Neurolmage,2009,45(1):S61-S72.

[15] X PENNEC.iLogDemons:a demons-based registration algorithm for tracking incompressible elastic biological tissues[J].International Journal of Computer Vision，2011(92):92-111.

[16] H LOMBAERT.Spectral Log-Demons:diffeomorphic image registration with very large deformations[J]. International Journal of Computer Vision,2014,107(3):254-271.

[17] G B HUANG,Q Y ZHU.Extreme learningmachine:theory and applications[J]. Neurocomputing,2006,70(1):489-501.

[18] G B HUANG. An insight into extreme learning machines: random neurons, random features and kernels[J].Cognitive Computation,2014(6):376-390.

[19] D E RUMELHAR,G E HINTON Williams.Learning representations by back-propagating errors[J].Nature,1986,323(6088):533-536.

[20] P J WERBOS.The roots of backpropagation:from ordered derivatives to neural networks and political forecasting[J].New York:Wiley,1994.

(责任编辑：孙 娟)

国家自然科学基金项目(61373127)

高弘治(1988-)，男，辽宁大连人，辽宁师范大学计算机与信息技术学院硕士研究生，研究方向为模式识别、图像配准；闫德勤(1962-)，男，辽宁沈阳人，博士，辽宁师范大学计算机与信息技术学院教授，研究方向为模式识别、机器学习；杨伊(1992-)，女，辽宁锦州人，辽宁师范大学计算机与信息技术学院硕士研究生，研究方向为模式识别、图像配准；刘彩凤(1992-)，女，内蒙古丰镇人，辽宁师范大学计算机与信息技术学院硕士研究生，研究方向为模式识别、图像配准。

10.11907/rjdk.162601

TP317.4

A

1672-7800(2017)003-0159-04