基于椭圆曲线密码体制的对称存储加密密钥保护方案
2017-04-13朱小松
朱小松
(杭州电子科技大学 通信工程学院,浙江 杭州 310018)
基于椭圆曲线密码体制的对称存储加密密钥保护方案
朱小松
(杭州电子科技大学 通信工程学院,浙江 杭州 310018)
存储重要数据的硬盘通常都会提供加密保护,为了防止加密硬盘数据的对称卷密钥丢失或泄露,必须对其采取安全保护措施。针对卷密钥的安全性管理问题,提出一种基于标准ECDH密钥交换协议改进协议的密钥保护方案。该协议可以确保客户端无需将其生成的公钥以及直接相关的密钥信息传输到网络中,因此客户端与服务器之间的通信传输网络无需采用加密隧道。
对称密钥;密钥管理;ECDH;椭圆曲线
0 引言
信息时代信息是一种资产,同其它任何资产一样,需要存储和保护。随着计算机的出现,信息存储被电子化,常见用于存储信息的存储设备包括硬盘、磁带、U盘等。由于硬盘具有容量大、数据传输速率快、寿命长等优点,因此硬盘已成为主要的外围存储设备,使用越来越广泛,特别是在企业存储体系架构中扮演着及其重要的角色。与内存不一样,存储在硬盘中的信息是非易失的。作为信息的直接载体,硬盘所面临的安全威胁更为严峻。现今比较流行的企业存储体系架构有DAS、NAS和SAN三类,硬盘在物理上是与主机分离的,不同的主机都需要利用光纤通道FC或SCSI协议通过路由器或交换机访问存储设备。在这种环境下,无可避免地会遭受信息窃取、篡改、监听等物理攻击。
为了解决存储于硬盘中的信息安全性问题,必须采取有效安全保护措施。加密技术是保护信息安全最有效的方式。加密技术又分为对称加密和非对称加密两类。在对称加密中,发送者和接收者双方必须使用相同的私有密钥;而在非对称加密中,发送者和接收者双方拥有自己的私钥,并且共享双方的公钥。由于对称加密算法具有加密速度快、效率高、计算量小等优点,因此直接用于加密信息。然而,由于加密和解密使用同样的密钥,这就使得密钥的安全性无法得到保障。在对称加密中,加密的安全性不仅取决于加密算法,密钥的安全性管理尤为重要。只要密钥没有泄露,那么加密的信息就是安全的,因此密钥管理就成为了信息安全系统中的一个关键性问题。本文对此提出一种新的密钥管理方案,它是在标准ECDH密钥交换协议的基础上改进来实现的,算法的安全性建立在椭圆曲线离散对数问题的基础之上。本文详细描述了算法的加密和解密过程,使用Java语言模拟了协议的加/解密过程,并对协议的性能和安全性进行了分析。最后,设计了一种安全性系统模型,并详细描述了解密过程中客户端的密钥获取过程。
1 预备知识
1.1 椭圆曲线公钥密码体制
椭圆曲线密码学(ECC)是一种基于椭圆曲线数学的非对称加密方法,它是由Neal Koblitz和Victor Miller于1985年提出的。在数学上,椭圆曲线(EC)是一类代数曲线,其中,基于有限域Zp的椭圆曲线方程[3]定义为:
(1)
基于有限域GF(2m)的椭圆曲线方程[6]定义为:
(2)
椭圆曲线公钥密码体制的域参数为(q,a,b,G,n,h)[4]。
q为素数p或者q=2m。a和b是式(1)和式(2)中椭圆曲线方程的系数,常用的椭圆曲线是非奇异性的,即:4a3+27b2≠0。G是椭圆曲线上的基点,n是点G的大素数阶,且n是使得n×G=O成立的最小正整数。h是一个由椭圆曲线的阶除以n产生的余因子,并且h≤4。
1.2 椭圆曲线离散对数问题
将ECC中的加法运算与RSA中的模乘运算相对应,将ECC中的乘法运算与RSA中的模幂运算相对应。要建立基于椭圆曲线的密码体制,需要类似因子分解两个素数之积或者求离散对数这样的“难题”[5]。
考虑方程Q=k×P,其中Q,P∈Eq(a,b),且k 客户端与服务器共同商议一组共享参数:椭圆曲线Eq(a,b)、椭圆曲线的基点G以及点G的大素数阶n。系统加/解密流程如图1所示。 图1 加/解密流程 2.1 加密过程 (1)服务器生成一个随机数s作为私钥,0≤s≤n-1,并计算其公钥S=s×G,然后服务器将自己的公钥S通过网络发送给客户端,自己保存私钥s。 (2)客户端生成一个随机数c作为其私钥,0≤c≤n-1,并计算其公钥C=c×G。 (3)客户端计算出K=c×S,这个K就是用来加密硬盘卷密钥P的秘密钥。加密完成后,客户端立即丢弃自己的私钥c和秘密钥K,并在客户端磁盘合适的位置保存自己的公钥C以及服务器的公钥S。 2.2 解密过程 (1)客户端生成一个随机数e作为临时密钥,0≤e≤n-1,并计算E=e×G以及X=C+E。客户端将X通过网络发送给服务器。 (2)服务器接收到X后,计算Y=s×X,并将Y返回给客户端。 (3)客户端先计算出Z=e×S,然后计算出K=Y-Z。于是,客户端就恢复出秘密钥K。 2.3 Java实现协议过程 使用Java语言模拟协议加/解密过程的代码如下: publicstaticvoidmain(String[]args)throwsInsecureCurveException, NotOnMotherException,NoCommonMotherException{ /** * 加密过程 */ Randomr1 =newRandom(500); BigIntegerc=newBigInteger(300,r1); /* 客户端生成一个随机数作为私钥 */ System.out.println("client: " +c); Randomr2 =newRandom(100); BigIntegers=newBigInteger(250,r2); /* 服务器生成一个随机数作为私钥 */ System.out.println("server: " +s); /* 分别给定3个参数:a,b和p,确定椭圆曲线Ep(a,b),其中,a和b是椭圆曲线方程y^2=x^3+a*x+b的系数,p是一个大素数 */ EllipticCurveec=newEllipticCurve(newBigInteger("-485640"), newBigInteger("1456878"),newBigInteger("78596435759")); System.out.println("EllipticCurve: " +ec+ "createdsuccessfully!"); /* 生成椭圆曲线的基点G*/ ECPointG=newECPoint(ec,newBigInteger("1494207"),newBigInteger("122304")); ECPointC,S; C=G.multiply(c); /* 计算出客户端的公钥C=c*G*/ System.out.println("C=c*G: " +c+ " * " +G+ " = " +C); S=G.multiply(s); /* 计算出服务器的公钥S=s*G*/ System.out.println("S=s*G: "+s+ " * " +G+ " = " +S); ECPointK1; K1 =C.multiply(s); /* 计算出加密秘密钥K1=s*C*/ System.out.println("K1: " +K1); /** * 解密过程 (2)沉箱码头段沉箱顶标高+1米,当地设计最高水位+3.24米,沉箱处水深较浅,施工船舶难以进入沉箱路侧区域施工;且沉箱陆侧水域面积较小,抓斗船无法布置船位; */ Randomr3 =newRandom(500); BigIntegere=newBigInteger(300,r3); /* 客户端生成一个临时密钥 */ ECPointE; E=G.multiply(e); /* 客户端计算E=e*G*/ ECPointX; X=C.add(E); /* 客户端计算X=C-E*/ ECPointY; ECPointZ; Z=S.multiply(e); /* 客户端计算Z=e*S*/ ECPointK2; K2 =Y.subtract(Z); /* 客户端计算解密秘密钥K2=Y-Z*/ System.out.println("K2: " +K2); /* 判断加密秘密钥K1与解密秘密钥K2是否相等 */ System.out.println(K2.equals(K1)); } 编译所得结果如下所示: client:190226479994559504786272223906036427100364197 0776253246225407203279979900505454350489415681 server:11870294321146830125036280966927097374490375 11491420923142353313157808297293 EllipticCurve:y^2 =x^3 + -485640x+ 1456878 (mod78596435759 )createdsuccessfully! C=c*G:19022647999455950478627222390603642710 03641970776253246225407203279979900505454350489415681 * (1494207, 122304) = (57479944285, 9576960236) S=s*G:11870294321146830125036280966927097374 49037511491420923142353313157808297293 * (1494207, 122304) = (25405216404, 36628324820) K1: (68016581895, 19353883045) K2: (68016581895, 19353883045) true 3.1 性能分析 从网络传输与密钥大小两方面来分析算法的性能。 (1)网络传输。客户端与服务器通过网络传输进行数据通信。假设在解密过程中,客户端并没有生成临时密钥。在加密过程相同的前提下,如果想要客户端恢复秘密钥,则客户端需要将自己的公钥通过网络发送给解密服务器,服务器计算。显然,这需要采用安全隧道传输,例如SSL/TLS协议。在本算法中,客户端通过生成一个临时密钥来约束这两个值,只有客户端自己才能解绑,而攻击者则不行,因此无需采用加密隧道。 (2)密钥大小。这与标准的ECDH算法相当。与其它传统的算法相比,160位的ECC密钥安全性等价于1 024位的DSA/RSA密钥,224位的ECC密钥安全性等价于2 048位额DSA/RSA密钥[9]。显然,不仅这缩小了算法的计算量,而且密钥所需的存储空间更小。 3.2 安全性分析 如果客户端丢弃了自身的私钥,没有连接到解密服务器,则无法恢复秘密钥。所需要考虑的安全性问题主要有以下三种情况: (1)中间人攻击[7]。窃听者截获到客户端发送的以及接收到的数据。由于这些元数据都被客户端所提供的临时密钥约束,只有客户端自身可以对这些值进行解绑,因此可以抵御中间人攻击。 (2)客户端的公钥的安全性保护。客户端需要对自己的公钥提供安全性保护,以防止泄露。可以采取设置设备权限和文件系统权限,配置安全性架构(如SELinux)或者使用硬件加密(如TPM),这些都是客户端可以实现的。 (3)服务器的私钥的安全性保护。解密服务器必须保护它的私钥。为了实现这个目的,服务器可以对文件系统的权限设置访问控制,并实施服务策略。此外,服务器还可以使用硬件加密(如HSM)来保护自己的私钥。 4.1 安全系统模型 该系统设计方案的安全系统模型如图2所示,主要包括3个模块:客户端、服务器和传输网络。 图2 安全系统模型 实施该方案的前提条件是客户端硬盘中的数据已经采用对称加密方式进行加密,如采用LUKS/cryptsetup加密,因此需要对加密数据的卷密钥采取安全性保护。在客户端中输入加密命令,客户端通过使用改进协议所生成的秘密钥对其进行加密保护。当用户需要访问硬盘数据时,客户端首先要通过网络连接到解密服务器,然后在客户端中输入相应的解密命令,使客户端与服务器各自执行相应的操作,从而客户端可以恢复解密卷密钥的密钥。 4.2 密钥获取 图3描述了解密过程中客户端获取密钥的过程: (1)客户端从硬盘中加载相关元数据,包括客户端自己的公钥以及服务器的公钥等。 (2)客户端与服务器通过改进协议进行数据交换,由于客户端采用临时密钥对指定元数据进行了处理,客户端并没有将自己的密钥和身份信息传输到网络中,因此无需采用加密隧道传输。 (3)客户端接收到服务器返回的数据后进行处理,恢复秘密钥,进而恢复硬盘卷密钥。最后,客户端利用卷密钥解密硬盘。 图3 密钥获取 本文针对ECDH改进协议提出了一种基于椭圆曲线公钥密码体制的对称存储加密密钥保护方案。针对协议的性能和安全性分析,提出了一种实现方案的系统模型以及解密过程中的密钥获取过程。但是,对于方案具体的实现过程还不够完善,这正是后续研究的方向。 [1] 高伟, 谷大武,侯方勇,等.磁盘数据安全保护技术综述[J].计算机应用研究,2008,25(5):1 288-1 291. [2] NATHANIEL MCCALLUM.Tang binding daemon [EB/OL]. https://github.com/latchset/tang. [3] BEHROUZ A.FOROUZAN.密码学与网络安全学[M].北京:清华大学出版社,2009:298-306. [4] 李胜金, 张昌宏,周大伟.一种基于ECDH的可认证密钥协商协议[J].信息安全与通信保密,2011,6(3):70-72. [5] PAUL GARRETT.密码学导引[M].北京:机械工业出版社,2003:337-345. [6] TURKI F,ALSOMANI,M K IBRAHIM,et al.High performance elliptic curve GF(2m) crypto-processor[J].Asian Network for Scientific Information,2006, 5(4): 742-748. [7] DAHAI DU,HUAGANG XIONG.A Dynamic key management scheme for MANETs[C].2011 Cross Strait Quad-Regional Radio Science and Wireless Technology Conference,2011: 779-783. [8] AKSHAY DESAI,KRISHNA ANKALGI,HARISH YAMANUR,et al.Parallelization of AES algorithm for disk encryption using CBC and ICBC modes[C]. 4th ICCCNT 2013,2013:647-650. [9] HUA YILIN.Hypercube routing protocol with secure data transmission mechanisms in sensor networks using elliptic curve diffie-hellman key agreements[C].2009 International Conference on New Trends in Information and Service Science,2009:1 303-1 308. (责任编辑:陈福时) 朱小松(1989-),男,湖北松滋人,杭州电子科技大学通信工程学院硕士研究生,研究方向为数据安全算法、云存储技术。 10.11907/rjdk.162659 TP309.7 A 1672-7800(2017)003-0153-032 改进算法描述
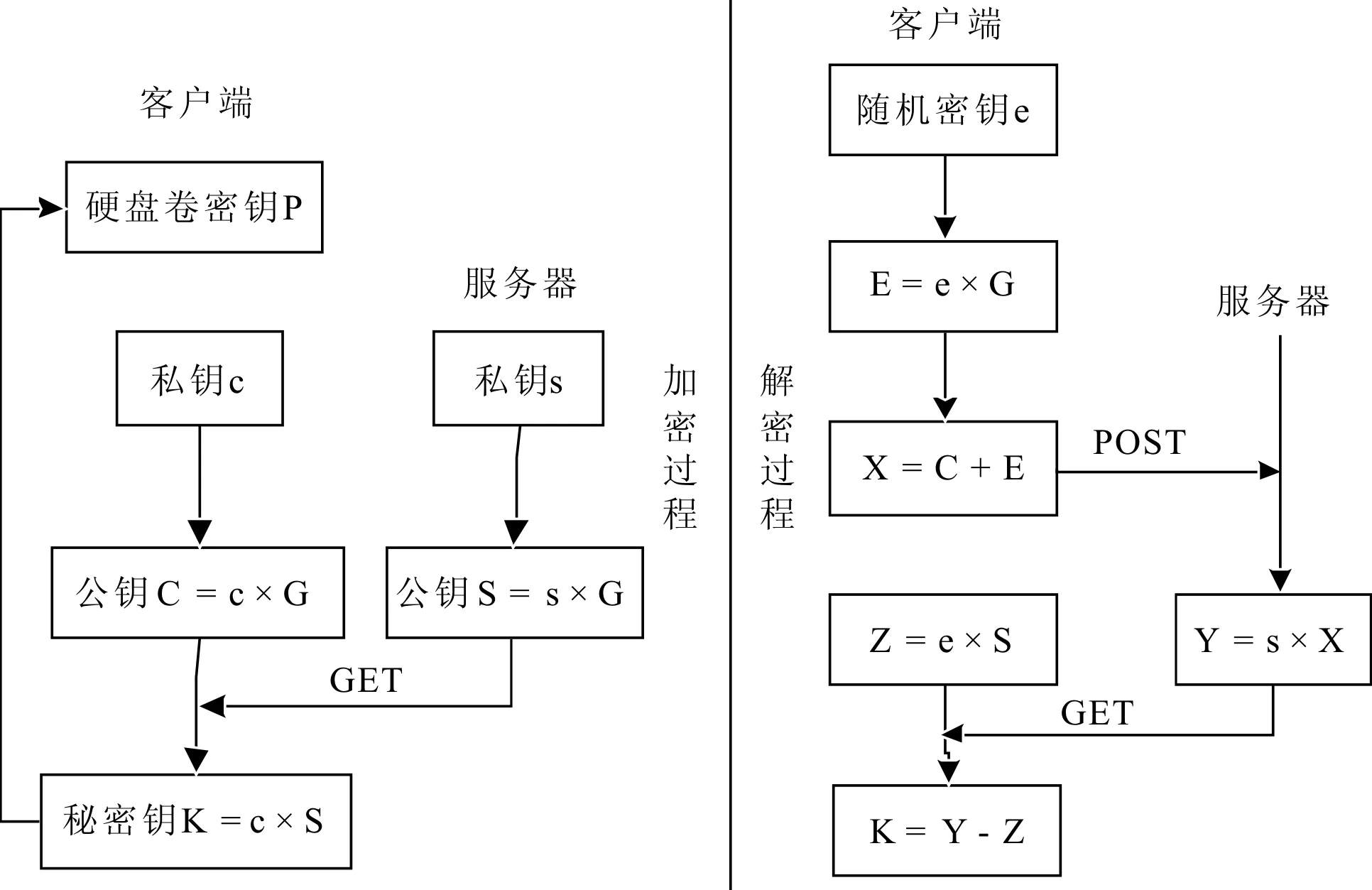
3 算法分析
4 系统设计方案
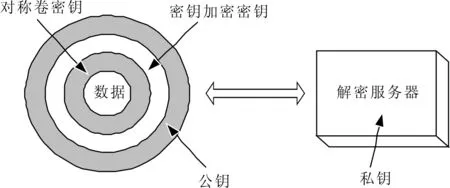
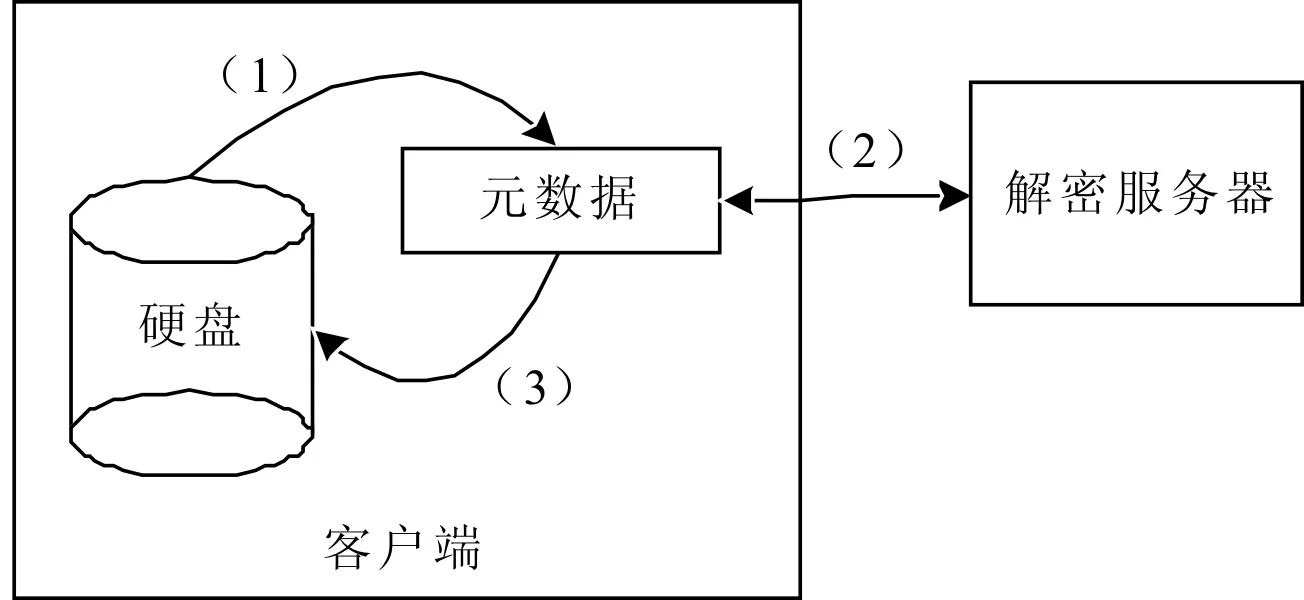
5 结语
