基于显著区域检测的SURF特征匹配优化算法

陈 谦，吴 清

(1.河北工业大学 计算机科学与软件学院；2.河北省大数据计算重点实验室，天津 300401)

基于显著区域检测的SURF特征匹配优化算法

陈 谦1,2，吴 清1,2

(1.河北工业大学 计算机科学与软件学院；2.河北省大数据计算重点实验室，天津 300401)

针对传统SURF匹配算法在特征点选取阶段选取了大量不符合匹配预期的特征点，增加了后期匹配的运算复杂度，提出一种SURF算子和显著区域检测相结合的方法。为使检测出的极值点和预期匹配的目标更加接近，用SURF算子构建出尺度空间图像后对该空间作显著区域检测，再对特征点赋显著度权值并通过孤立点剔除和局部冗余筛选出目标点，筛选后的特征点比传统方法得到的特征点数量明显减少，在降低时间复杂度的同时匹配精度提高了18%。特征匹配时引入RANSAC算法剔除误匹配点对，对匹配结果作进一步修正。实验表明，与传统SURF算法比较，改进算法在实时性和匹配精度方面均更优。

SURF算法；显著区域检测；尺度空间；特征值；匹配精度；RANSAC算法

0 引言

随着图像处理、机器视觉等相关领域技术的快速发展，特征匹配得到了广泛应用。在图像匹配方法中，特征点的提取及匹配方法已有很多研究成果。 Forstner算子[1]、Harris算子[2]、Moravec算子[3]、SIFT(scale invariant feature transform)算子[4]等都是比较常用的特征点提取算子。其中，SIFT算子是由David G·Lowe提出的一种基于局部特征的描述方法，但许多研究实验表明SIFT算法存在着128维的特征描述符，计算复杂度较高、实时性差、误匹配较多。SURF(speeded up robust features)算法[5]是SIFT算法的快速改进方法，虽然都具有对尺度和旋转的鲁棒性[6]，但相关实验表明，SURF算法采用二维Haar小波响应、积分图像和Hession矩阵相结合实现算法加速，比SIFT算法效率提升了3～5倍。

但是上述方法都存在特征点提取准确度低和误匹配的问题，为了减少不符合匹配预期特征点的个数，使提取的特征点与人眼观察的特征点相近。本文主要开展了以下几方面的工作：为了提高SURF算子主方向精度，提出了为Haar小波响应增加梯度权值来改变扇形区域内各特征点的价值贡献度；为了改善特征点选取，删除信息含量较低和冗余的点，提出了基于显著图、孤立点剔除、局部冗余三级特征点价值评价策略；为了降低匹配错误率，对匹配结果进行了RANSAC匹配检验。

1 SURF特征点提取与匹配

SURF描述子包含两个主要部分：检测关键点和计算特征。检测关键点采用快速Hession检测算法，特征描述采用Haar小波圆形区域方向直方图特征作为主特征，通过建立特征点附近区域内的信息作为细节描述子。

1.1 Hession矩阵检测特征点

设图像I(X)的某一像素点为X=(x，y)，则尺度为σ的Hessian矩阵H(X，σ)定义为[7]：

(1)

其中，Lxx(X，σ)是二阶高斯滤波∂2/∂x2g(σ)与图像点X的卷积。同理，可计算Lxy(X，σ) 和Lyy(X，σ)。但是在实际处理中，离散化高斯滤波器会有一些走样，所以采用 Bay等提出的盒滤波来近似高斯滤波。

如图1所示，采用该方法计算卷积时，其计算量与滤波器大小无关，可以极大程度地提高算法执行速度。图1第一行中x、y和xy方向的离散二阶斯导数用Lxx、Lyy和Lxy表示；第二行中x、y和xy方向的加权盒滤波器近似用Dxx、Dyy和Dxy表示。

当用σ= 1.2的高斯二阶微分滤波，模板尺寸为99最为最小的尺度空间值对图像进行滤波和斑点检测，Hession矩阵的行列式可作如下简化：

(2)

另外，响应值还要根据滤波器大小进行归一化处理，以保证任意大小滤波器的F范数是统一的。

图1 利用盒滤波器来近似高斯滤波器

1.2 构造SURF特征主方向和描述子

利用非极大值抑制初步确定特征点，然后采用三维线性插值法得到亚像素级的特征点。再统计特征点邻域内的Haar小波特征，选取最大值扇形的方向作为该特征点的主方向。最后在特征点周围取一个带方向正方形框，然后把该框分为16个子区域，每个子区域统计25个像素的水平方向dx和垂直方向dy的Haar小波特征。原理如图2所示。

图2 特征点描述算子构造

2 频率调谐显著区域检测算法

为了和SURF算法进行有机结合，本文选择复杂度较低的频率调谐显著检测算法[8]，算法中使用的高斯滤波器和尺度空间每一层使用的滤波器均相同，并随着层数的增加，不断扩大滤波器的尺寸。算法主要步骤如下：

(1)设输入图像为Iw×h，其中w为图像宽度，h为图像高度。用高斯滤波器对图像进行平滑处理，得到新的图像Ig，其计算公式如下：

(3)

(2)将图像Ig从RGB模型转换到Lab模型。对每个特征分别计算其整体均值得到均值图像Iμ=[Lμ,aμ,bμ],同时对各特征高斯平滑，得到平滑后的图像为：

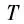
(4)

(3)计算得到显著图区域，即最终的显著图S(x,y)：

(5)

算法过程如图3所示。

3 融合显著区域检测的SURF算法

单纯的SURF匹配算法存在特征点过选取的问题，为此本文融合显著区域检测的方法，可以有效减少SURF算法中无意义的特征点，使匹配效率得到大幅提升。

图3 频率调谐显著图检测步骤

3.1 构建尺度空间

首先构建Hessian矩阵，利用式(2)得到近似Hessian矩阵行列式，使用该近似行列式来表示图像中某一点x处的斑点响应值，遍历图像中所有的像元点，形成在该尺度下所有点检测的响应图像。在建立金字塔图像空间时，采用不断增大的盒子滤波器模板尺寸，形成多尺度斑点响应的金字塔图像，利用这一金字塔图像，基于文献[9]中的思想进行斑点响应极值点搜索[9]。设金字塔滤波器响应长度l、滤波器尺寸S、组索引o、层索引t和尺度σ，有：

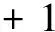
(6)

(7)

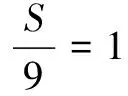
(8)

在进行尺度分析的情况下，随着尺度不断增大，被检测到的斑点数量迅速衰减。本文实验中的金字塔只建立到第三层，由于粗尺度上选取特征点的数量通常相对较少，所以在第二层和第三层可以采用隔点滤波，从而进一步加快运算效率。

3.2 显著区域检测及特征点精确定位

通过显著区域检测使特征点分布更加趋近显著区，但是依然存在特征点数量大和质量差的问题。为此，本文建立了以下三级价值评价策略，可以不断优化特征点数目，提高匹配精度。

3.2.1 基于显著图的特征点价值评价策略

SURF算子抛弃了SIFT算子中图像金字塔构建过程中输入图像反复与高斯函数的核卷积，并反复对其进行二次抽样，可避免大量的重复操作。

在此基础上，本文通过对各级尺度空间图像上作显著性区域检测得到尺度空间显著图，结合基于显著图的特征点价值评价策略为每个提取到的特征点分配相应的权值。具体处理过程可分为以下两步：首先，对显著性区域检测后的显著图作灰度图归一化；其次利用提取到的特征点响应值和归一化灰度图中该点的灰度值相乘，得到新的特征值作为评价标准。基于该策略使得处于显著区域的特征点特征得到增强，处于背景区的特征点特征被削弱。

3.2.2 基于孤立点剔除的特征点价值评价策略

虽然通过显著图可以筛去大量处于背景中的特征点，但仍有一部分显著区外特征值较低的离散特征点无法去除。为此，本文采用基于孤立点剔除的策略解决这一问题。在特征点方向分配中，以特征点为中心，计算半径为6s(s为特征点所在的尺度值)的邻域内的点在x、y方向的Haar小波响应，在此Haar小波边长取4s[10]。

孤立点是在低密度区域中的特征点，且认为一个数据集中若存在孤立点，那么孤立点的密度会小于平均密度[11]。下面定义每个对象密度的计算方法，标准化原始数据集后，计算n个对象两两之间的距离di,j，形成距离矩阵R：

(9)

设所有对象的平均距离为D，为与平均密度的定义保持一致，在计算每个对象i的对象密度时，将有效直径延长至原来的3倍，以3D为单位封闭区间的面积，扫描数据矩阵R，计算每个对象单位封闭区间的对象数Ci，也就是与对象i间距离小于3D/2的对象点数目。因此，每个对象i的对象密度为：

(10)

但是复杂的对象密度计算牺牲了大量时间复杂度，影响了算法整体效率，在此对算法作以下简化：

(1)计算出单位面积图像中特征点密度d。

(2)统计以特征点Si为中心，半径6s(s为特征点所在的尺度值)的范围内特征点数量m。

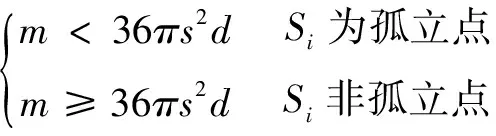
当该特征点为孤立点时剔除该孤立点，否则保留，如图4所示d1～d5五个孤立点将被剔除。

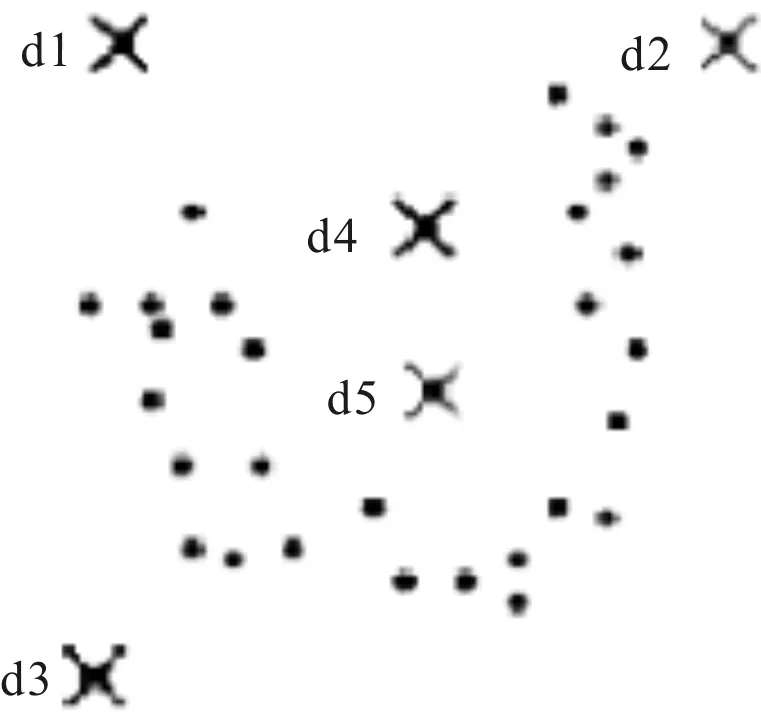
图4 孤立特征点检测示意图

3.2.3 基于局部冗余的特征点价值评价策略

以特征点为中心，张角为的扇形区域滑动，计算窗口内的Harr小波响应值dx、dy的累加，在累加过程中由于距离中心越远的点对特征点的影响越小，实验中通过为Haar小波响应增加梯度权值使得主方向的计算更加精准。

生成特征描述子后，特征点在显著区域分布较为紧密，匹配时互相干扰太大，为此需进一步对局部冗余的特征点进行筛除。将以特征点为中心，M(可根据图片分辨率和期望获得的特征点个数确定，本文M取3s)为半径范围内的特征点全部去除，确保局部只有一个有效特征点，降低了相似点之间的干扰，提高了匹配精度。

3.3 RANSAC算法剔除误匹配点

RANSAC算法的基本假设是样本数据中包含正确数据，也包含异常数据，即数据集中含有噪声[12]。这些异常数据可能是由于多种因素导致，包括错误的测量、假设或计算等产生的。SURF匹配算法中，这些异常数据可能由 SURF算法进行预匹配产生的错误或者误差比较大的匹配导致的。

3.3.1 RANSAC算法

本文采用RANSAC算法，实现步骤如下：

(1)通过选取总数为n的最小抽样集(n为初始化所需最小样本数)和样本集P(P样本集大于n)，在P样本集中随机选取n个样本数据，得到P的子集S，用来对模型M进行初始化。

(2)得到的余集为SC=P/S，此样本集与模型M的误差小于某一阈值t(t为预设值)的样本集合与S构成集合S*。S*是内点集，它们构成S的一致集。

(3)如果#(S*)>=N，认为模型参数正确，并利用集S*，采用最小二乘法重新计算新的模型M*。重新随机抽取新的子集S，并重复以上操作。

(4)反复对样本进行抽样，一定次数后如果没有找到一致集，则算法失败；反之，根据最大一致集判断内外点，直到算法结束。

3.3.2 SURF算法与 RANSAC算法结合

为了通过RANSAC算法可以有效剔除误匹配点，具体过程如下：首先，从SURF算法预匹配结果中随机取出一些特征匹配点对，计算出变换矩阵；再根据得到的变换矩阵遍历预匹配中得到的所有匹配对，计算所有预匹配对中在特定阈值下满足该变换矩阵模型的百分比。重复上面的过程n次，比较每个变换矩阵下满足该模型的匹配对百分比，选取对应百分比最大的矩阵作为最终得到的最佳变换矩阵。将在该最佳变换下误差大于特定阈值的特征匹配对去除。再用去除后的特征匹配对重复上述步骤m次。

匹配过程具体参数设置如下：a是通过SURF算法预匹配后得到的特征匹配点对数；b是通过RANSAC算法进行去污匹配后所剩下的特征匹配点对数。当满足式(11)关系时放弃所有的匹配点对，整个过程找出来的匹配点对数则为0[13]。

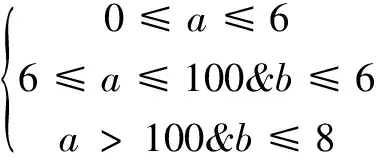
(11)

整个匹配过程如下：分别读入两幅图像，对两个图像进行特征点匹配，当两个图像中找到的匹配点正好为对方的时候匹配成功，否则匹配失败，然后用RANSAC算法去除预匹配中的误匹配。

4 实验结果分析

本文算法用MATLAB R2012a实现。本文考虑了光照、旋转、缩放等多种因素，选择了大量的实验图片，比较了传统SURF算法与本文算法在特征点匹配性能上的差异。

4.1 频率调谐显著区域检测实验结果

频率调谐算法处理过程简单有效，图5给出了所做实验中几幅图像的处理结果，其中(a)、(c)为原图，(b)、(d)为显著性检测后的结果。可以看出频率调谐算法有很好的特征区域提取效果。为了避免在Lab空间3个均值图像分量进行特征融合时，灰度值有可能超过有效显示范围的问题，本文对显著图的结果进行了归一化处理。

图5 显著图检测结果

4.2 本文算法得到的特征点结果

基于得到的显著图，利用本文提出的分级筛选机制，对特征点进行提取实验。图6所示为其中的一幅图像的实验结果，其中，(a)为原图，(b)为传统方法得到的特征点，(c)为通过显著图筛选后的特征点，(d)为通过孤立点剔除筛选后的特征点，(e)为通过局部冗余筛选后的特征点。可以看出，随着特征点分布的不断优化，没有分布在显著区域中的缺少匹配价值的点、处在背景区里孤立的点、相似度较高的冗余点相继被筛除，留下了最具有匹配价值的点，从而使特征点的精度和质量得到提高。另外，由于特征点的减少，计算时间和最终匹配效率都得到了优化。

图6 特征点筛选结果

由表1可以得出，提取的特征点越多，所用的时间越多。因此采用本文算法来减少特征点提取个数在时间效率方面有很大改善。

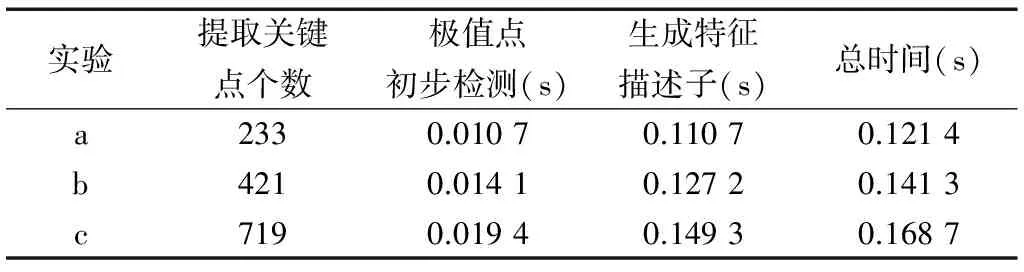
表1 SURF算法时间分配比较

4.3 融合后的SURF匹配

特征点选取直接影响SURF算法的运算复杂度，如图7所示，其中，(a)为传统的SURF匹配结果，(b)为本文改进的SURF方法匹配结果。本文提出的算法更加优化了特征点的选择，特征点数量得到了控制，减少了特征点描述子生成的时间。而且进一步的匹配实验结果表明，通过本文算法可以最大程度保证特征点落在视觉更加显著的有效区域内。

图7 实验结果对比

在特征向量匹配时，采用最简单的两向量内积最大值为最匹配的点，设定阈值n，只有当这个最大值大于该阈值方可认为两特征点匹配，通过优化后的匹配点选择，找到了相似性更高的匹配点，降低了误匹配。最后再通过RANSAC算法对特征匹配点对进行检测，筛选出错误的匹配，进一步优化匹配效果。

根据表2可得，传统SURF算法的效率和准确率都有缺陷，本文算法在这两方面都进行了优化，尤其是在匹配准确率上得到了较大的优化，比传统算法平均准确率提升了18%以上。

表2 本文算法与传统SURF匹配对比结果

5 结语

传统SURF匹配算法存在的不足，通过本文提出的方法得到了有效解决。显著性区域检测和特征点筛选使得特征点的数量有效减少，特征描述子和匹配速度得到了一定提升，RANSAC算法检测使得匹配过程中出现的误匹配进一步得到优化。但是实验结果对显著区域检测结果有一定的依赖，所以本文提出的方法在目标相对显著的图像中能够达到更好的效果。

[1] FRSTNER W,GLCH E. A fast operator for detection and precise location of distinct points, corners and circular features[C]. ISPRS intercommission conference on fast processing of photogrammetric data，1987:281-305.

[2] HARRIS C.A combined corner and edge detector[C].Alvey Vision Conference,1988:147-151.

[3] MOREVEC H P. Towards automatic visual obstacle avoidance[C].International Joint Conference on Artificial Intelligence.1977:584-584.

[4] LOWE D G. Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision,2004,60(60):91-110.

[5] BAY H,TUYTELAARS T,GOOL L V. SURF:speeded up robust features[J].Computer Vision & Image Understanding,2006,110(3):404-417.

[6] CECCARELLI M,MUSACCHIA F,PETROSINO A.A fuzzy scale-space approach to feature-based image representation and retrieval[M].Brain, Vision, and Artificial Intelligence. Springer Berlin Heidelberg, 2005:377-385.

[7] SCHLEICHER J,TYGEL M,HUBRAL P I.Hessian matrices[M].Society of Exploration Geophysicists, 2007.

[8] ACHANTA R, HEMAMI S, ESTRADA F, et al. Frequency-tuned salient region detection[C].IEEE International Conference on Computer Vision and Pattern Recognition (CVPR 2009).2009:1597-1604.

[9] CHEUNG W,HAMARNEH G.Dimensional scale invariant feature transform[J].IEEE Transactions on Image Processing,2009,18(9):2012-2021.

[10] NANDI S,GUHA P,VENKATESH K S.Objects from animacy:joint discovery in shape and haar feature space[C].Computer Vision, Graphics & Image Processing, 2008. ICVGIP '08. Sixth Indian Conference on. 2008:730-737.

[11] 陆声链, 林士敏. 基于距离的孤立点检测及其应用[J]. 计算机与数字工程, 2004, 32(5):94-97.

[12] LEBEDA K,MATAS J,CHUM O.Fixing the locally optimized RANSAC[C].British Machine Vision Conference,2012.

[13] 陈艺虾,孙权森,徐焕宇,等.SURF算法和RANSAC算法相结合的遥感图像匹配方法[J].计算机科学与探索,2012,6(9):822-828.

(责任编辑：陈福时)

河北省自然科学基金项目(F2015202239)；天津市科技计划项目(14RCGFGX00846)

陈谦(1991-)，男，陕西兴平人，河北工业大学计算机科学与软件学院硕士研究生，研究方向为图像处理和模式识别；吴清(1965-)，女，湖北钟祥人，博士，河北工业大学计算机科学与软件学院教授，研究方向为图像处理和模式识别。

10.11907/rjdk.162587

TP312

A

1672-7800(2017)003-0022-04