基于K-L变换的无线信道密钥提取方法

李古月 胡爱群

(东南大学信息科学与工程学院, 南京 210096)

基于K-L变换的无线信道密钥提取方法

李古月 胡爱群

(东南大学信息科学与工程学院, 南京 210096)

为了解决基于无线信道特征的密钥生成方案中信道特征测量值不互易且高度冗余的问题, 提出了一种基于K-L变换的无线信道密钥提取方法．首先,将K-L变换划分为信号分组、变换矩阵计算和信号变换3个部分,并对各个部分进行数学建模,分别阐明了有交互和无交互2种K-L变换的特点．然后,计算了交互协方差矩阵或变换矩阵引起的信息泄露率,并分析了2种变换的计算复杂度．结果表明,有交互的K-L变换可以提高密钥的一致性,降低计算复杂度,泄露信息足以忽略,更加适用于无线信道密钥生成．

密钥生成;物理层安全;K-L变换; 相关系数; 特征向量

随着无线设备(如平板电脑、智能手机等)的迅速普及,无线通信在人们生活中的作用也日益重要．对于无线支付和社交网络等具有高风险与私密性的业务而言,无线通信的安全性是其进一步蓬勃发展的前提要素．传统的安全方案中,对称加密方案需要额外的密钥分发过程,而非对称加密方案则面临计算复杂度高的问题[1-2]． 近年来,基于无线信道密钥生成的物理层安全方案得到了广泛关注．该方案利用无线信道电磁波传播的互易性特征,将无线信道作为生成对称密钥的天然随机源,避免了复杂的密钥分发过程[3-4]．然而,实际系统中采集到的无线信道特征受时延、设备指纹及测量噪声等因素的影响,存在较大的差异性[4-5]．时域过采样技术与频率和空间的多元化技术(如正交频分复用和多输入多输出)可以用于提高密钥的生成速率[6-9],但同时也会引发信道特征样本在时域、频域和空间域的相关性,造成数据冗余,最终导致生成密钥熵降低．针对上述问题,文献[5,10]分别运用时域插值和对数域差分的方法改善时延和设备指纹对信道特征差异性的影响．文献[11-12] 采用K-L变换来提高信道特征的互易性,但在公共信道上进行了协方差矩阵和特征向交互,增加了窃听者窃取生成密钥的几率,而且没有对有交互和无交互2种K-L变换进行系统对比分析,交互协方差与特征向量引起的利弊关系未得到明确阐述．

本文提出了一种基于K-L变换的无线信道密钥提取方法,研究了有交互和无交互的2种K-L变换在密钥一致性、信息泄露率和计算复杂度上的优劣．

1 系统模型

图1描述了无线通信场景的系统模型．图中,Eve表示潜在的窃听者;Alice和Bob表示希望建立安全通信的2个合法用户,他们利用多径信道的互易性与时变性,在两端独立生成一致的安全密钥并不断更新;d=0.5λ为相干距离,其中λ为波长,对于2.4 GHz的无线通信系统,d=6.25 cm．位于合法用户相干距离以外的用户观测到的信道与合法用户所观测得的信道可视作统计独立的[11]．

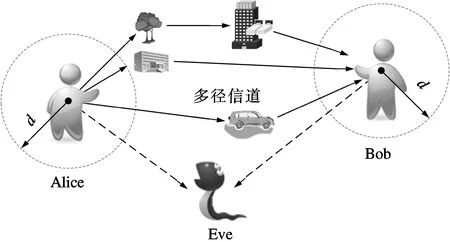
图1 无线通信系统模型

本文中研究的信道为移动无线信道,通信系统为正交频分复用(orthogonal frequency division multiplexing, OFDM)系统,采用时分双工(time division duplex, TDD)模式．首先,Alice与Bob先后发送导频探测信道,通过信道估计等方法获取信道特征参数(如信号幅度、包络、相位等)．本文中使用的信道特征参数为信道状态信息(channel state information,CSI)．假设时延与硬件指纹造成的测量值差异已经通过插值变换及硬件校准等方法去除．定义M×N维矩阵XA和XB分别为Alice和Bob端经过处理后得到的信道特征信号,其中M为OFDM子载波个数,N为时间的采样点数．XA和XB之间的关系表述式为

XB=XA+W

(1)

式中,W表示由测量噪声及校准处理所残留的噪声等引起的观测偏差,与XA相互独立．本文中假设W为彩色高斯噪声,方差为RW．观测偏差将降低信道特征信号的互易性,XA和XB中的相邻元素间存在高度冗余性．

2 K-L变换

K-L变换是一种建立在统计特性基础上的线性变换,也是均方误差意义下的最优变换,在数据压缩与去噪方面得到了普遍运用[11]．无线信道密钥生成中的K-L变换主要包括信号分组、变换矩阵计算和信号变换3个部分．根据Alice与Bob在变换矩阵计算部分有无交互,可将K-L变换分为有交互的K-L变换和无交互的K-L变换．

2.1 信号分组

首先,对Alice与Bob端的信号矩阵XA和XB进行分割重组处理,即

(2)

(3)

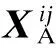
(4)

(5)

式中,l=NF(i-1)+j;vec{·}为按列拉直操作．

将拉直后的每个向量看作一个样本,则重组后的P×Q维信道特征信号矩阵由Q组样本构成,即

(6)

(7)

式中,Q=NF×NT．为了统计信息的准确性,样本组数和维度应满足Q≥P．

xB=xA+w

(8)

(9)

2.2 变换矩阵计算

K-L变换是一种与统计信息相关的变换,其变换矩阵由统计信息的特征向量组合构成．变换矩阵计算主要包括特征值分解与变换矩阵构建．

2.2.1 有交互的K-L变换

在有交互的K-L变换中,Alice与Bob可以交互协方差矩阵或变换矩阵．

当交互信息为协方差矩阵时,Alice与Bob根据以下步骤计算变换矩阵:

(10)

(11)

(12)

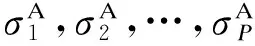
③ Alice和Bob将特征值矩阵和特征向量矩阵按照特征值从大到小的顺序排序,排序后的特征值矩阵和特征向量矩阵分别为

(13)

(14)

(15)

(16)

④ Alice与Bob选用排序后的前K个特征向量构建变换矩阵VA和VB,其中

(17)

(18)

式中,K为特征向量个数,由Alice和Bob根据误码率需求提前商定．

当交互信息为变换矩阵时,Alice与Bob根据以下步骤计算变换矩阵:

④ Alice按照式(17)构建变换矩阵VA,并将变换矩阵通过公共信道发送给Bob．Bob将变换矩阵VA赋值给变换矩阵VB,即

VB=VA

(19)

2.2.2 无交互的K-L变换

在无交互的K-L变换中,Alice与Bob根据以下步骤计算变换矩阵:

① Alice和Bob分别计算各自的协方差矩阵,即

(20)

③ Alice和Bob分别按照式(13)～(16)对特征值矩阵和特征向量矩阵进行重排．

④ Alice和Bob分别按照式(17)和(18)构建变换矩阵VA和VB．

2.3 信号变换

Alice与Bob分别利用变换矩阵对重组后的信道特征信号矩阵实行变换,即

(21)

(22)

3 性能对比

3.1 密钥一致性

将互相关系数作为密钥一致性的评价准则．定义γm(m∈{1,2,…,K})为Alice与Bob的第m个变换信号分量间的互相关系数,则

(23)

由式(21)和(22)可得

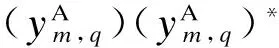
(24)

(25)

(26)

式中,

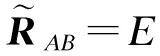
(27)

(28)

(29)

故有交互的K-L变换的互相关系数为

(30)

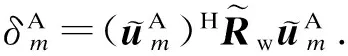
在无交互的K-L变换中,

(31)

(32)

由于

(33)

故无交互的K-L变换的互相关系数为

(34)

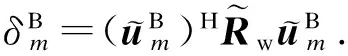
(35)

(36)

根据式(35)和(36)可得

(37)

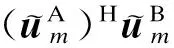
(38)

由此可知,相比无交互的K-L变换,有交互的K-L变换可以获得更高的密钥一致性．

3.2 信息泄露率

在公共信道上交互信息会引起信息泄露．当泄露的信息足够多时,窃听者可以通过暴力破解等方式窃取密钥信息．

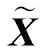
假设信道特征信号的取值为1,2,…,R,其中R的大小取决于模数转换器的精度．交互协方差矩阵造成的信息泄露率的上界为

ρ=Rθ2-θ1

(39)

由此可知,尽管有交互的K-L变换会引起信息泄露,但是信息泄露率低,不足以让窃听者通过泄露的信息有效推测出密钥信息．

3.3 计算复杂度

在K-L变换的3个部分中,信号分组与信号变换相对于变换矩阵计算的计算复杂度小,因此本文重点比较变换矩阵计算中2种K-L变换的计算复杂度．在变换矩阵计算中,协方差矩阵计算和特征值分解的计算复杂度较高,矩阵传递与排序等操作的计算复杂度较低．

在有交互的K-L变换中,Alice需要承担协方差矩阵计算和特征值分解运算, Bob的计算复杂度较低．在交互协方差矩阵的K-L变换中,Bob无需计算协方差矩阵,仅需承担特征值分解运算．在交互变换矩阵的K-L变换中,Bob无需计算协方差矩阵和分解特征值,计算复杂度非常低．而在无交互的K-L变换中,Alice和Bob均需要承担协方差矩阵计算和特征值分解的运算,计算复杂度较高．因此,无交互的K-L变换的计算复杂度高于有交互的K-L变换,无交互的K-L变换适用于Alice与Bob均具有较强计算能力的环境．当Alice和Bob中一方的计算能力较弱时,交互变换矩阵的K-L变换更为适用．

4 仿真结果

无线信道模型采用3GPP提出的SCM中的非视距城市信道模型．OFDM系统载波中心频率为2 GHz,带宽为3.84 MHz,载波数M=256．时间采样点数N=1 024,采样间隔为0.5 ms,移动速率为10 m/s．

图2比较了不同信噪比下有交互和无交互的K-L变换的互相关系数．由图可知,随着信噪比的增大,2种K-L变换的互相关系数均逐渐增加,趋近于1．此外,随着分量序号m的增大,2种K-L变换的分量互相关系数迅速降低．

(a) 有交互的K-L变换

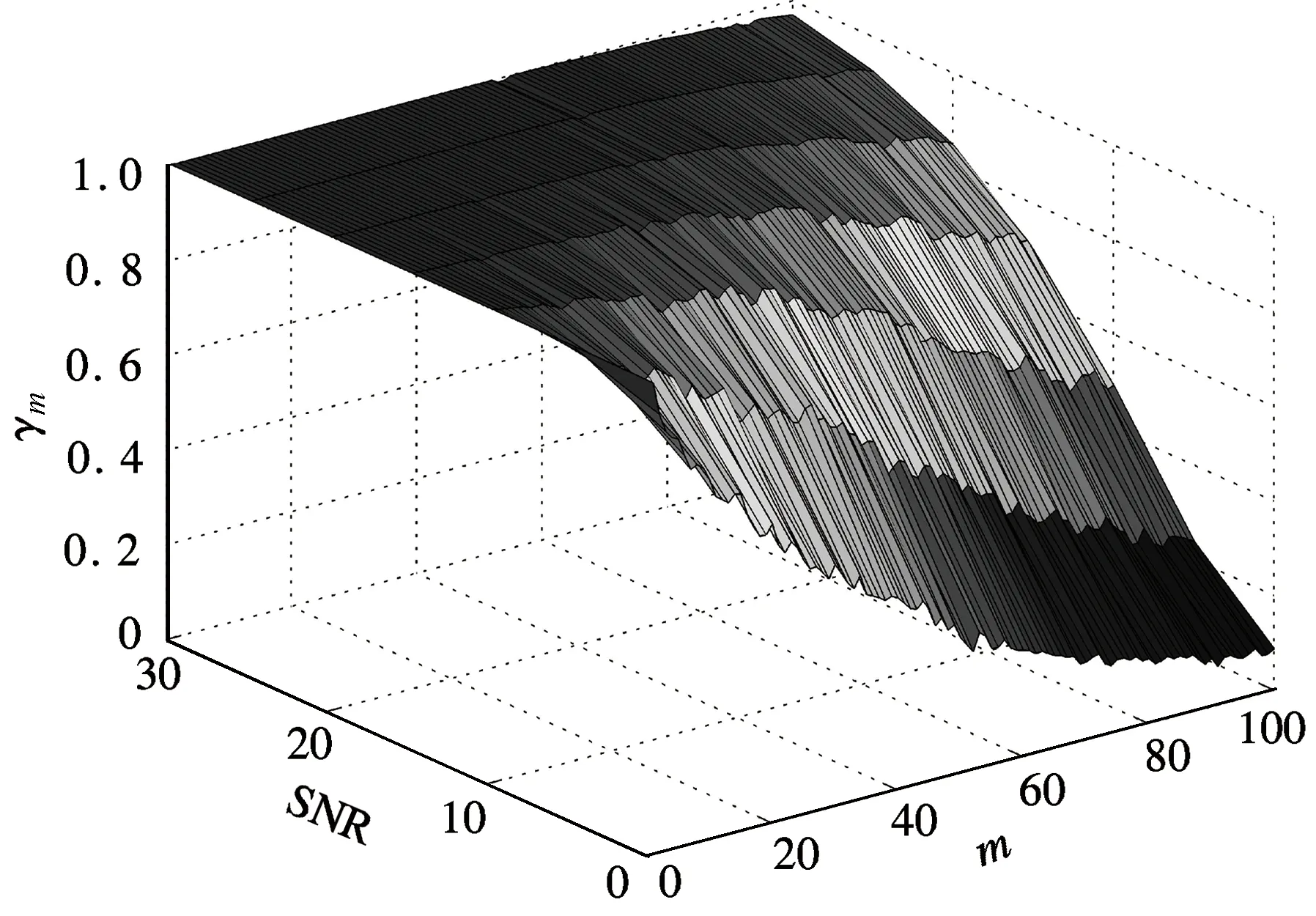
(b) 无交互的K-L变换

图3比较了10 dB信噪比下原始信号以及2种K-L变换中前8个分量的互相关系数．由图可知,原始信号的互相关系数较低,且各个分量的互相关系数无显著变化．有交互和无交互的K-L 变换中各个分量的互相关系数随着分量序号的增加而降低,且明显高于原始信号．有交互的K-L 变换的互相关系数高于无交互的K-L变换,从而证实了第3节中的结论．

图3 K-L变换的互相关系数对比

不同变换方法下的自相关系数如图4(a)所示．由图可知,利用2种K-L变换方法都能显著降低原始信号的自相关系数,减少信号的冗余．图4(b)描述了有交互的K-L变换中不同子矩阵维度下的自相关系数．由图可知,子矩阵块的维度越大,自相关系数下降得越快,但同时特征值分解的计算复杂度也越大,因此,子矩阵维度大小需要在冗余度与计算复杂度中作折中．

(a) 不同变换方法

(b) 不同子矩阵维度

5 结语

本文对K-L变换的信号分组、变换矩阵计算和信号变换3个部分依次建立模型,系统地对比分析了有交互和无交互的K-L变换的特点和优劣．结果表明,2种K-L 变换均可以有效地降低数据冗余．信号分组中子矩阵维度的大小需要折中考虑冗余度与计算复杂度．有交互的K-L变换可以有效提高信道特征的互易性,降低计算复杂度,信息泄露率极小．因此,有交互的K-L 变换更加适用于基于K-L变换的无线信道密钥提取方法．

References)

[1]Diffie W, Hellman M. New directions in cryptography[J].IEEETransactionsonInformationTheory, 1976, 22(6): 644-654. DOI:10.1109/tit.1976.1055638.

[2]Bloch M, Barros J, Rodrigues M R D, et al. Wireless information-theoretic security [J].IEEETransactionsonInformationTheory, 2008, 54(6): 2515-2534. DOI:10.1109/tit.2008.921908.

[3]李古月, 胡爱群, 石乐. 无线信道的密钥生成方法[J]. 密码学报, 2014,1(3): 211-224. DOI:10.13868/j.cnki.jcr.000020. Li Guyue, Hu Aiqun, Shi Le. Secret key extraction in wireless channel [J].JournalofCryptologicResearch, 2014, 1(3): 211-224. DOI:10.13868/j.cnki.jcr.000020. (in Chinese)

[4]Zenger C T, Zimmer J, Pietersz M, et al. Exploiting the physical environment for securing the Internet of things [C]//ProceedingsoftheACMNewSecurityParadigmsWorkshop. Enschede, the Netherlands, 2015: 44-58. DOI:10.1145/2841113.2841117.

[5]Gopinath S, Guillaume R, Duplys P, et al. Reciprocity enhancement and decorrelation schemes for PHY-based key generation [C]//2014IEEEGlobecomWorkshops. Austin, TX,USA, 2014: 1367-1372. DOI:10.1109/glocomw.2014.7063624.

[6]Mathur S, Reznik A, Ye C, et al. Exploiting the physical layer for enhanced security: Security and privacy in emerging wireless networks [J].IEEEWirelessCommunications, 2010, 17(5):63-70. DOI:10.1109/mwc.2010.5601960.

[7]Zeng K, Wu D, Chan A, et al. Exploiting multiple-antenna diversity for shared secret key generation in wireless networks [C]//IEEE29thConferenceonComputerCommunications. San Diego, CA,USA, 2010: 1-9. DOI:10.1109/infcom.2010.5462004.

[8]Wallace J W, Sharma R K. Automatic secret keys from reciprocal MIMO wireless channels: Measurement and analysis [J].IEEETransactionsonInformationForensicsandSecurity, 2010, 5(3): 381-392. DOI:10.1109/tifs.2010.2052253.

[9]Liu H, Wang Y, Yang J, et al. Fast and practical secret key extraction by exploiting channel response [C]//IEEE32thConferenceonComputerCommunications. Turin,Italy, 2013: 3048-3056.DOI:10.1109/infcom.2013.6567117.

[10]Patwari N, Croft J, Jana S, et al. High-rate uncorrelated bit extraction for shared secret key generation from channel measurements [J].IEEETransactionsonMobileComputing, 2010, 9(1): 17-30. DOI:10.1109/tmc.2009.88.

[11]Li G, Hu A, Zou Y, et al. A novel transform for secret key generation in time-varying TDD channel under hardware fingerprint deviation [C]//IEEE82ndVehicularTechnologyConference. Boston, MA,USA, 2015: 1-5. DOI:10.1109/vtcfall.2015.7390807.

[12]Chen C, Jensen M A. Secret key establishment using temporally and spatially correlated wireless channel coefficients [J].IEEETransactionsonMobileComputing, 2011, 10(2): 205-215.

Secret key extraction algorithm for wireless channel based on K-L transform

Li Guyue Hu Aiqun

(School of Information Science and Engineering, Southeast University, Nanjing 210096, China)

To solve the problem of non-reciprocity and high redundancy of channel characteristic measurements in secret key generation algorithm based on wireless channel characteristics, a secret key extraction approach based on K-L transform is proposed. First, the K-L transform is divided into three parts including signal partition, transform matrix calculation, and signal transform. The corresponding mathematical model of each step is established. The characteristics of two K-L transforms with and without interaction are clarified, respectively. Then, the information leakage rate caused by covariance or transform matrix interaction is calculated, and the computational complexities of these two transforms are analyzed. The results show that the K-L transform with interaction can enhance key agreement, reduce computational complexity and lead to negligibly small information leakage, making it more applicable for secret key generation from wireless channel.

secret key generation; physical layer security; K-L transform; correlation coefficient; eigenvector

10.3969/j.issn.1001-0505.2017.02.001

2016-07-18. 作者简介: 陈萍(1983—)，女，博士生；熊蔚明(联系人)，男，研究员，博士生导师，xwm@nssc.ac.cn.

国家高技术发展计划(863计划)资助项目(2011AA7033045).

陈萍,熊蔚明.一种可用于莱斯衰落信道的信噪比估计算法[J].东南大学学报(自然科学版),2017,47(2):209-214.

10.3969/j.issn.1001-0505.2017.02.002.

TN918.82

A

1001-0505(2017)02-0203-06