MIMO-OFDM移动水声通信系统中多普勒扩展估计方案

张 行 宋 康,2 李春国 杨绿溪 方世良

(1东南大学水声信号处理教育部重点实验室, 南京 210096)(2青岛大学电子信息学院, 青岛 266071)

MIMO-OFDM移动水声通信系统中多普勒扩展估计方案

张 行1宋 康1,2李春国1杨绿溪1方世良1

(1东南大学水声信号处理教育部重点实验室, 南京 210096)(2青岛大学电子信息学院, 青岛 266071)

为了消除MIMO-OFDM移动水声通信系统中的多普勒效应,提出了一种训练序列结构及其相应的多普勒扩展估计方案.发射端在每一帧信号前插入2段相同的训练序列,接收端使用多个并行相关器对接收到的2段训练序列进行自相关运算,根据输出的最大自相关值所对应的相关器窗口长度即可进行多普勒扩展因子估计.仿真结果表明,与传统的以LFM信号为训练序列的估计方案相比,所提方案充分利用了MIMO技术提供的分集增益,进行更为精确的多普勒扩展因子估计,估计误差低于2×10-3.

水声通信;多输入多输出;正交频分复用;多普勒扩展

带宽和频谱利用率是影响通信系统信息传输速率的2个关键因素.MIMO技术利用多个换能器同时发射和接收信号,显著提高了频谱利用率,因而在带宽受限的水声通信系统中得到了广泛的关注和研究,单载波传输[1]和OFDM多载波传输[2-3]中都引入了MIMO技术.OFDM技术将频率选择性衰落信道划分为多个正交子信道,每个子信道频率平坦衰落,以避免符号间干扰,但多普勒效应会破坏其子载波间的正交性,影响系统性能.对于移动水声通信系统,由于声波在海水中的传播速度仅为1 500 m/s[4],收发端移动引起的多普勒效应远大于陆地无线通信[5-6].因此,必须在信号同步阶段估计出多普勒扩展因子,并根据该扩展因子对接收信号重采样[7],消除多普勒效应的影响.

现有的多普勒扩展估计算法大多使用LFM信号作为前后同步信号[5,8],接收端利用已知的序列与接收信号进行互相关运算,根据前后同步信号输出的峰值间隔与实际信号间隔的差值计算多普勒扩展因子.这类算法存在2个缺点:① 接收机需要缓存所有的接收数据才能计算前后同步信号的峰值,不利于实时信号处理;② 接收信号与本地已知信号作互相关运算,无法消除收发端晶振频率差异等引起的信号频率偏移的影响.

本文提出了一种适用于MIMO-OFDM移动水声通信系统的训练序列结构及其相应的多普勒扩展估计方案,该方案的估计精度远高于传统的以LFM信号为训练序列的估计方案.

1 系统模型

设MIMO-OFDM系统的发射换能器数为Nt,接收换能器数为Nr.信号采用基于循环前缀(cyclic prefix,CP)的OFDM调制方式,以防止码间干扰.令B为信道带宽,K为子载波个数,则子载波间隔为Δf=B/K,一个OFDM符号的持续时间为T=1/Δf=K/B,每个OFDM符号的循环前缀时间长度为Tg.

本文所采用的训练序列频域结构为IEEE 802.11n协议中40 MHz混合模式前导码的HT-LTF部分[9].训练序列包含2个相同的OFDM符号.令s={s0,s1,…,sK-1}T表示一个OFDM符号的频域序列,发送信号的帧结构如图1所示,图中sIFFT为s的逆傅里叶变换,即sIFFT=IFFT(s).

图1 发送信号的帧结构

第m帧基带信号为

(1)

经频率为fc的载波变频,得到的带通信号为

(2)

(3)

时变多径水声信道的冲激响应为

(4)

式中,δ()为单位冲激函数;Ap(t)和τp(t)分别为第p条路径的增益和时延.参考文献[10],进行如下假定:① 所有路径的多普勒扩展因子相同,即τp(t)≈τp-at,其中a为多普勒扩展因子;② 路径时延、路径增益和多普勒扩展因子在一帧信号持续时间内保持不变.

经过上述信道,接收端第r个接收换能器上的接收信号为

(5)

(6)

将接收信号下变频为基带信号,即

(7)

式中,w(t)为基带高斯白噪声;Ω=2πafc为载波频偏.

(六)三叉形器。良渚诸多墓穴出土了三叉形玉器，这种器是做什么用的，至今没有定论，比较普遍的看法是，这种三叉形玉器是良渚人的冠饰，不是一般人，而是部落首领将其戴在额头上。这种说法不是没有道理的，三叉形器不多，一般一墓只有一件，且放置在墓主人的头部。各墓出土的三叉形器体制差不多，不同的主要是中间的竖梁，有长有短。三叉形器的造型类似汉字“山”。如果将它与圆雕玉鸟比对一下，当发现它们其实是很相像的，所不同的，仅在于玉鸟的双翅是平的，而三叉形器的两边类翅的两叉向后弯曲，如果将三叉形器理解成飞鸟的造型，那么这双翅的靠后就有点变形了，这种变形为的是突出鸟飞得快。

在接收端以F倍过采样率进行采样,可得基带数字信号为

(8)

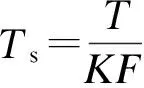
2 延时自相关算法

在水声通信系统中,传输信号受到多普勒效应影响而产生较大的时间扩展或压缩,因此,传统的延时相关算法不能直接应用于接收端的同步.本文采用在接收端使用多个并行相关器对信号进行处理的方法[5],实现多普勒扩展因子的估计.如图2所示,q个相关器的相关窗口分别取不同的长度K1,K2,…,Kq,对接收信号进行延时自相关运算,得到判决变量M1,M2,…,Mq,再选取其中的最大值Mmax,根据Mmax对应的相关器窗口长度即可估计出多普勒扩展因子.

图2 多个并行相关器示意图

第q个相关器对接收信号中的2段重复序列进行自相关处理,得到自相关函数为

(9)

第q个相关器的能量函数为

yr(q+n+Kq)(yr(q+n+Kq))*]

(10)

第q个相关器的判决变量为

(11)

(12)

令c为声波在海水中的传播速度,则发射端与接收端的相对运动速度为

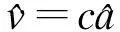
(13)

3 仿真试验

通过大量的仿真实验,对本文提出的估计方案进行性能测试,并与传统的以LFM信号为训练序列的估计方案(简称LFM方案)进行比较.仿真参数设置如下:信道带宽为10 KHz,2段训练序列总长度为25.6 ms,子载波数目为128,循环前缀长度为子载波数目的1/4,载波频率为27 KHz,过采样率为8,MIMO结构分别设置为1发1收、2发2收和4发4收.参照文献[11-13]中的多径瑞利衰落信道模型和参数,本文仿真时采用的2种信道模型为:① 信道模型1包含3条路径,其时延分别为0,0.5,1.0 ms,路径增益分别为0,-4.3,-8.7 dB;② 信道模型2包含7条路径,其时延分别为0,0.5,1.0,1.5,2.0,2.5,3.0 ms,路径增益分别为0,-4.3,-8.7,-13.0,-17.0,-21.0,-26.0 dB.

根据多普勒扩展因子估计值与实际值的误差来评判该方案的估计性能,该误差的计算公式为

(14)

图3(a)给出了a=0.005时信道模型1的估计误差曲线.由图可知,LFM方案与本文方案的估计误差均随信噪比(SNR)增加而减小,且当SNR>2 dB时,2种方案的估计误差曲线都趋于平稳.即使在较高的SNR下,LFM方案的估计误差仍然约为2×10-3,估计精度不高,在较低的SNR下,估计误差则更大;而本文方案在SNR=-5 dB时,估计误差接近1×10-3,并随SNR的增大,逐渐接近于0,估计精度较之于LFM方案有明显的提升.另外,在SNR较低时,利用MIMO技术可以获得一定的分集增益,2发2收系统较之于1发1收系统可以获得1 dB左右的性能增益,同样地,4发4收系统较1发1收系统可以获得2～3 dB的性能增益.

(a) 信道模型1

(b) 信道模型2

图3(b)给出了a=0.005时信道模型2的估计误差曲线图.比较图3(a)与(b)可知,LFM方案的估计误差随多径数目的增加略有增加,这是因为LFM方案是利用本地已知信号与接收到的最强径信号进行匹配来计算峰值的,多径数目越多,多径干扰越严重,从而导致其估计误差增加;而本文方案的训练序列结构中存在循环前缀,可以有效抵抗多径干扰,稳定性较强,多径数目的增加对估计误差影响不大.

图4给出了a=0.009时2种信道模型的估计误差曲线.与图3对比可知,随着a的增大,LFM方案的估计性能逐渐变差,当SNR=-5 dB时,LFM方案的估计误差大于7×10-3;而本文方案的估计误差则低于2×10-3,对多普勒扩展因子的估计更为精确,且具有较强的稳定性.同时可以看出,4发4收系统较之于1发1收系统可以获得约5 dB的性能增益.

(a) 信道模型1

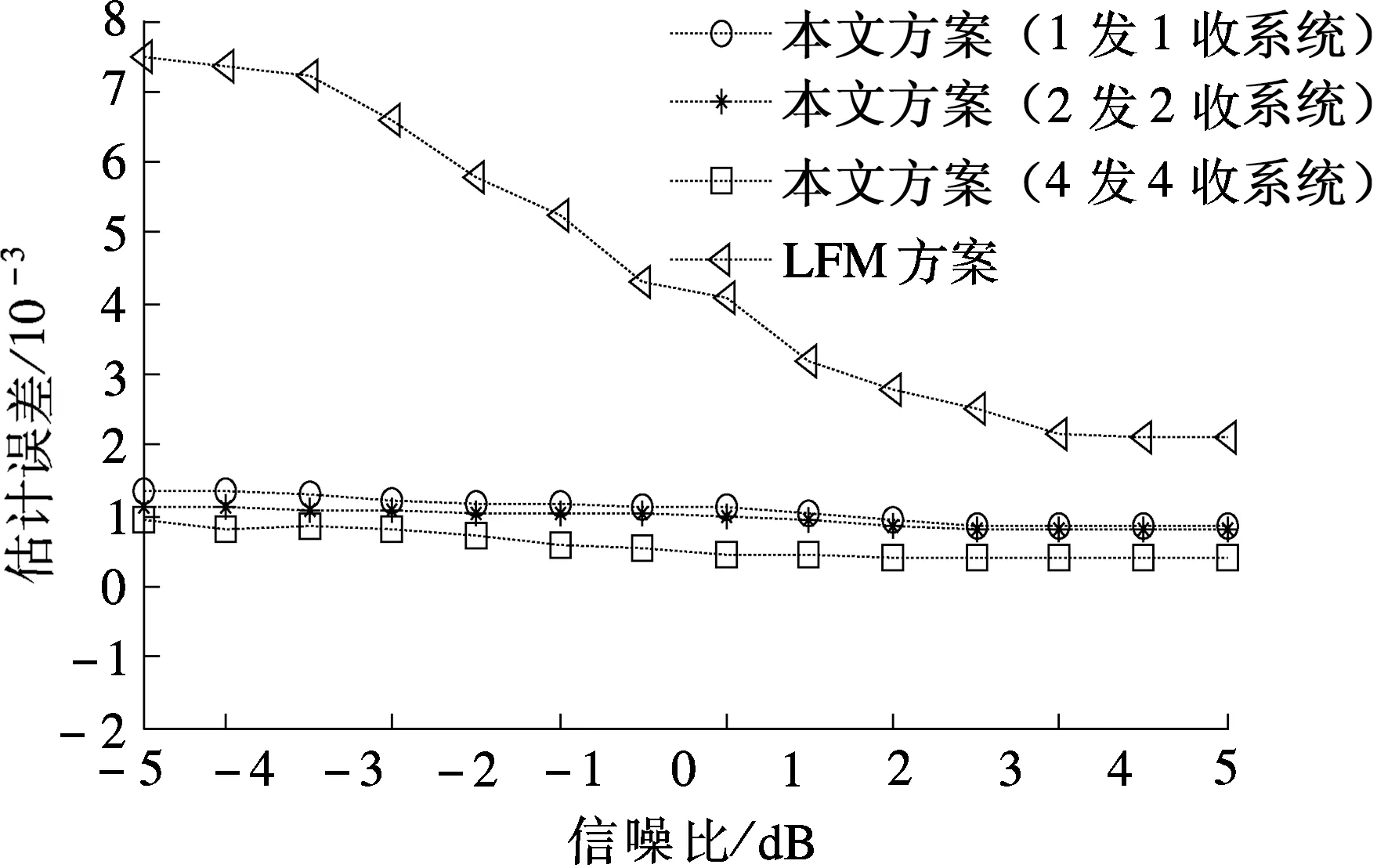
(b) 信道模型2

4 结语

本文分析了水声信道的特点以及多普勒效应对传输信号的影响,提出了一种适用于MIMO-OFDM移动水声通信系统的训练序列结构,并在接收端使用延时自相关算法进行多普勒扩展因子估计.仿真试验结果表明,与LFM方案相比,所提方案具有更高的估计精度和更强的稳定性.

References)

[1]Roy S, Duman T M, McDonald V, et al. High-rate communication for underwater acoustic channels using multiple transmitters and space-time coding: Receiver structures and experimental results [J].IEEEJournalofOceanicEngineering, 2007, 32(3): 663-688. DOI:10.1109/joe.2007.899275.

[2]Carrascosa P C, Stojanovic M. Adaptive MIMO detection of OFDM signals in an underwater acoustic channel[C]//2008IEEEOCEANS.Quebec City,Canada,2008:1-7. DOI:10.1109/oceans.2008.5151953.

[3]Zhang L, Li M, Li G. Symbol estimation for MIMO underwater acoustic communication based on multiplicative noise model[C]//2014IEEEInternationalConferenceonCommunicationProblem-Solving(ICCP 2014). Beijing, China,2014: 507-509.

[4]Ranjani G, Sadashivappa G. Characterization of underwater acoustic channels[C]//2015InternationalConferenceonAppliedandTheoreticalComputingandCommunicationTechnology(iCATccT).Nanjing, China,2015:523-528. DOI:10.1109/icatcct.2015.7456940.

[5]Sharif B S, Neasham J, Hinton O R, et al. A computationally efficient Doppler compensation system for underwater acoustic communications[J].IEEEJournalofOceanicEngineering, 2000, 25(1): 52-61. DOI:10.1109/48.820736.

[6]Qu F, Wang Z, Yang L, et al. A journey toward modeling and resolving Doppler in underwater acoustic communications[J].IEEECommunicationsMagazine, 2016, 54(2): 49-55. DOI:10.1109/mcom.2016.7402260.

[7]Daoud S, Ghrayeb A. Using resampling to combat Doppler scaling in UWA channels with single-carrier modulation and frequency-domain equalization [J].IEEETransactionsonVehicularTechnology, 2016, 65(3): 1261-1270. DOI:10.1109/tvt.2015.2409560.

[8]Sharif B S, Neasham J, Hinton O R, et al. Adaptive Doppler compensation for coherent acoustic communication[J].IEEProceedings—Radar,SonarandNavigation, 2000, 147(5): 239-246. DOI:10.1049/ip-rsn:20000665.

[9]Perahia E,Stacey R.NextgenerationwirelessLANs:Throughput,robustness,andreliabilityin802.11n[M]. Cambridge:Cambridge University Press, 2008:82-87.

[10]Li B, Zhou S, Stojanovic M, et al. Multicarrier communication over underwater acoustic channels with nonuniform Doppler shifts[J].IEEEJournalofOceanicEngineering,2008, 33(2):198-209.

[11]Chen Z, Zheng Y R, Wang J, et al. Synchronization and Doppler scale estimation with dual PN padding TDS-OFDM for underwater acoustic communication[C]//2013OCEANS.San Diego, CA, USA,2013:1-4.

[12]Zhao Y, Yu H, Wei G, et al. Parameter estimation of wideband underwater acoustic multipath channels based on fractional Fourier transform[J].IEEETransactionsonSignalProcessing,2016, 64(20):5396-5408.DOI:10.1109/tsp.2016.2582466.

[13]Xu T, Tang Z, Leus G,et al. Multi-rate block transmission over wideband multi-scale multi-lag channels[J].IEEETransactionsonSignalProcessing, 2013,61(4):964-979. DOI:10.1109/tsp.2012.2230169.

Doppler scale estimation scheme for MIMO-OFDM mobile underwater acoustic communication system

Zhang Xing1Song Kang1,2Li Chunguo1Yang Lüxi1Fang Shiliang1

(1Key Laboratory of Underwater Acoustic Signal Processing of Ministry of Education, Southeast University, Nanjing 210096, China)(2School of Electronic and Information Engineering, Qingdao University, Qingdao 266071, China)

To eliminate the Doppler effect in the multiple-input multiple-output orthogonal frequency division multiplexing (MIMO-OFDM) mobile underwater acoustic communication system,a training sequence structure and the corresponding Doppler scale estimation scheme were proposed.The transmitter inserts two identical training sequences ahead of each signal frame, while the receiver uses several parallel correlators to calculate the autocorrelation of the two received training sequences.Then, the Doppler scale factor can be estimated according to the window length of the correlator with the maximum autocorrelation value. The simulation results show that, compared with the traditional estimation scheme using the linear frequency modulation (LFM) signal as the training sequence, the proposed scheme can estimate the Doppler scale factor more accurately by fully utilizing the diversity gains of the MIMO technique, and the estimation error is less than 2×10-3.

underwater acoustic communication; multiple-input multiple-output(MIMO); orthogonal frequency division multiplexing(OFDM); Doppler scale

10.3969/j.issn.1001-0505.2017.02.003

2016-08-17. 作者简介: 张行(1992—),女,硕士生;李春国(联系人),男,博士,副教授,博士生导师,chunguoli@seu.edu.cn.

国家自然科学基金资助项目(61372101,61671144)、东南大学优秀青年教师教学科研资助计划资助项目.

张行，宋康,李春国,等.MIMO-OFDM移动水声通信系统中多普勒扩展估计方案[J].东南大学学报(自然科学版),2017,47(2):215-219.

10.3969/j.issn.1001-0505.2017.02.003.

TN929.3

A

1001-0505(2017)02-0215-05