基于迭代学习控制的桥式起重机定位及防摆
2017-04-12付子义袁海国王艺龙
付子义, 袁海国,2, 王艺龙
(1. 河南理工大学 电气工程与自动化学院, 河南 焦作 454003; 2. 郑州电力高等专科学校, 郑州 450000)
基于迭代学习控制的桥式起重机定位及防摆
付子义1, 袁海国1,2, 王艺龙1
(1. 河南理工大学 电气工程与自动化学院, 河南 焦作 454003; 2. 郑州电力高等专科学校, 郑州 450000)

针对桥式起重机在小车运行时引起负载摆动,影响工作效率、易引发事故和重复运行时的规律优化控制问题,提出利用迭代学习控制来对桥式起重机进行定位及防摆控制。用拉格朗日(Lagrange)方程建立桥式起重机的数学模型,对桥式起重机进行定位防摆控制仿真。结果表明,迭代学习控制可以利用桥式起重机重复运行的特性来对其进行高精度跟踪,同时有效地抑制负载摆角。
桥式起重机; 迭代学习; 拉格朗日方程; 定位及防摆; 重复运行
0 引 言
桥式起重机结构简单、承载量大而被广泛地应用于各类材料的起吊、输送和装配,不仅降低了工作者的劳动强度,而且使生产率得以大幅提高。然而,起重机在工作时载物的摇摆严重影响了桥式起重机的运行,甚至增加了事故发生的可能性,因此设计出有效的既可以跟踪小车又可以抑制摆角的控制方法成为研究的热点。
国内外学者对桥式起重机的定位与防摇问题做了大量研究。文献[1]中从非线性的角度出发,推导出桥式起重机非线性数学模型,从而对其进行防摆控制研究。文献[2]中将桥式起重机看成欠驱动系统,对其进行轨迹规划和防摆控制。文献[3]中建立了桥式起重机简易数学模型,基于简易模型设计了最短运输时间,并且设计了考虑残余摆动在内的S型最优曲线轨道。文献[4]中从快速定位的角度规划了一条轨迹,从抗摆的角度设计了一种抗摆环节,最后将两者结合在一起,并对轨迹参数进行了优化。文献[5]中将PID控制器进行了非线性优化,将优化后的控制器施加桥式起重机。此外,模糊控制[6-7]、神经网络控制[8-9]等智能控制也被应用于起重机的防摆中。上述方法都取得了一定的效果,但在对摆角控制的过程中影响了小车的运行速度,并且小车的定位不够精确,对摆角控制有待进一步提高。
桥式起重机在运行时做重复性的动作,其主要表现在:对同一批次的货物(如集装箱),货物质量相同,货物的装载点相同,卸载点相同,运行轨迹也一样。对于做重复运动的被控系统,迭代学习控制是一种比较理想的控制方法[10-11]:它对被控对象的运动具有记忆和改进功能,经过对被控对象不断地进行尝试控制,在控制的过程中进行自我学习,并将系统输出的轨迹与给定的期望轨迹进行比较,通过两者的偏差来对不理想的信号进行修正,进而产生更加精准的控制信号来提高系统的跟踪性能。本文根据拉格朗日方程建立桥式起重机的数学模型,并针对模型设计了迭代学习控制算法,通过仿真验证算法的有效性。
1 桥式起重机的模型建立
桥式起重机是一个典型的动力学系统,根据其动力学特性,采用拉格朗日方程来建立起重机的数学模型[12-13],如图1所示。
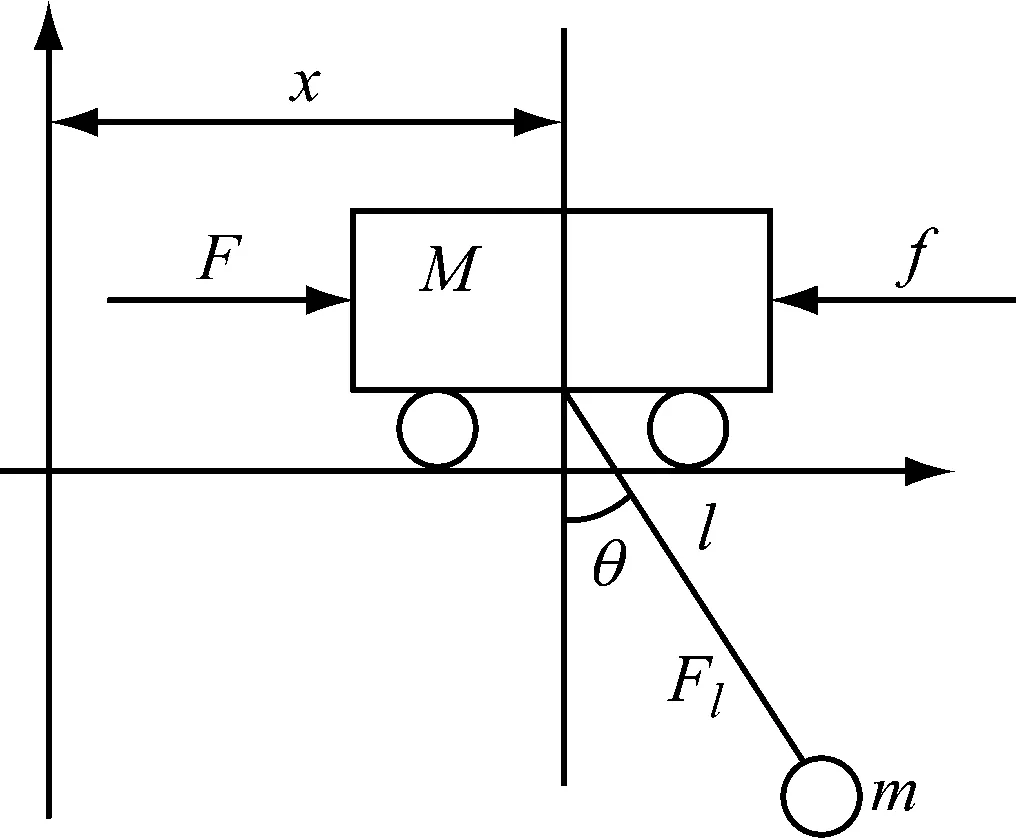
图1 桥式起重机的二维模型
设小车的质量为M,负载的质量为m,钢绳长度为l,负载与竖直线的夹角为θ,小车受到的驱动力为F,受到的阻力为f,钢丝绳的提升力为Fl。则可以得到在广义坐标下系统的拉格朗日方程组:
(1)

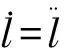
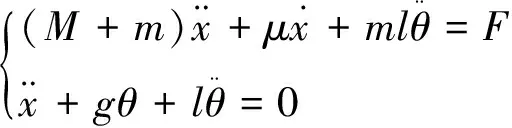
(2)
根据式(2),桥式起重机的状态空间方程变为:
(3)
式中:
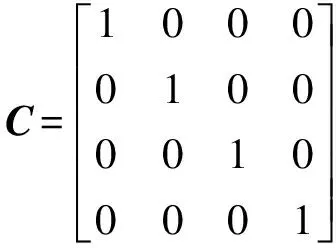
2 迭代学习控制器的设计
当桥式起重机做重复运输的运动时,其状态空间方程如下:
(4)
式中,k为桥式起重机运行次数。
在实际运行中,式(4)满足下列要求:① 系统的期望轨迹yd(t)是已知的,并且能够达到;② 系统在每次运行时的期望初态和运行初态是不变、相等的,即满足xd(0)不变,且xk(0)=xd(0)。
桥式起重机在每次运行时,轨迹都是已知的,可达到的,并且在每次运行时,货物的装载点和卸货点不变,因此两个条件都可以满足。
为了便于对算法的收敛性进行分析,先给出范数定义。对于n维向量W=(w1,w2,…,wn)T,范数定义为
(5)
对应的n×n矩阵A的范数为:
(6)
式中,λmax(·)为最大特征值。

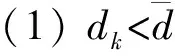

假设 当初态为xd(0)时,存在ud(t),并且产生的状态xd(t)符合:
yd(t)=Cxd(t),本文利用改进的PD型算法,利用uk+1,1,uk+1,2, …,uk+1,i-1分量来代替uk,1uk,2…,uk,i-1分量,其学习律为:
(7)
式中,ek(k)=yd(t)-yk(t),k为迭代次数;L、Γ为增益矩阵。

证明 由式(7)可以得到PD型的具体形式:

(8)
式中:uk,m表示uk的第m个分量:

(9)
对上式整理得:

(10)
则:

(11)
记:
则PD型迭代学习律转化成:
(12)
故

(13)
由假设可以得到:

(14)
对式(14)两边进行求导可得:

(15)
将式(14)和式(15)代入式(13),可得

(16)
对式(16)两端取范数可得到:
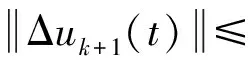
(17)
对式(17)两边同时乘以e-λt并取λ范数,可得
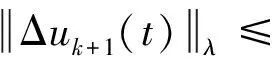
(18)
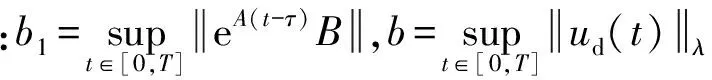
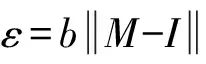

由引理可知:
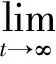
由假设可以得到:
对两边同取λ范数,可以得到:
再由误差式
联立上式推导可以得到:
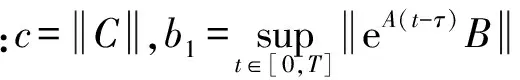
证毕
3 实验仿真
本文采用Matlab软件进行仿真,参数设置为:M=3 kg,m=6 kg,l=1.2 m,g=9.8 m/s2,μ=0.2,设置采样时间t=0.01 s。在每次运行开始,小车的位移初始位移相同,并设为xk(0)=0,摆角的初始位置位于竖直状态,每次运行时也相同, 即θk(0)=0。设小车的期望位移如图2所示,摆角的期望值为零。

图2 期望位移
运用式(13)的学习律:

小车位移跟踪情况如图3所示,k表示迭代次数。从中可以看出,当迭代次数比较少时,小车的实际输出轨迹与期望轨迹有较大的误差;当迭代次数k比较大时,如k=20时,小车的实际输出位移能够很好地跟踪于期望位移。当迭代次数k=20时,负载摆角的输出情况如图4所示,负载摆角的最大值约为0.099 rad,能够达到实际运行要求。
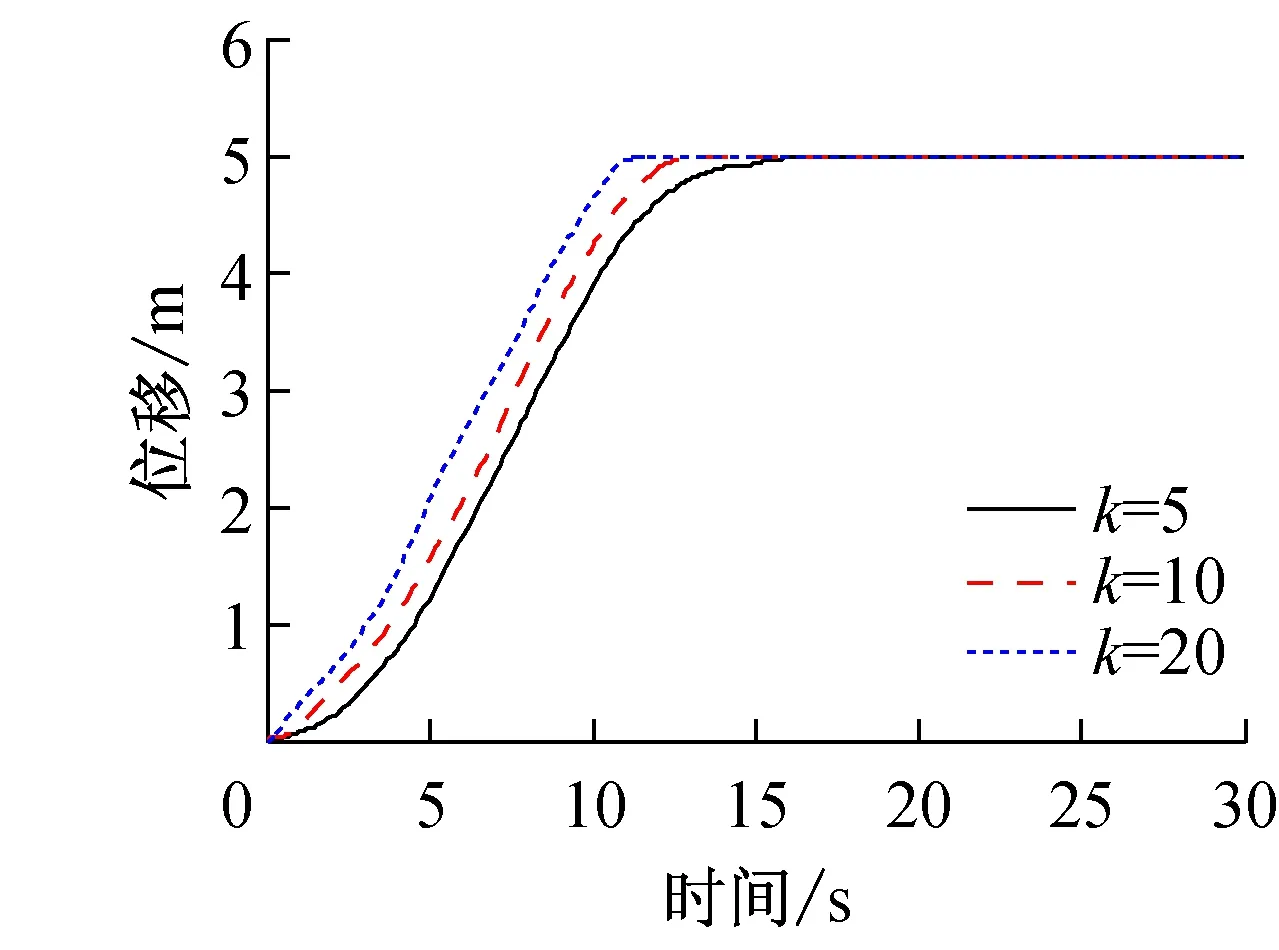
图3 位移跟踪结果

图4 摆角跟踪结果
4 起升质量对防摆效果的影响
在桥式起重机运行的过程中,对另一批次等质量货物进行运输时,不同批次的负载质量可能有差别,为研究负载质量对防摆的影响,假设对质量m=4 kg的同一批次和m=8 kg的同一批次货物分别运输时,绳长保持不变,分别研究小车位移跟踪和负载摆角情况,对收敛性的分析和上述证明过程一样,不再赘述。由式(3)可以看出,负载质量的改变不影响B和C的值,因此学习律仍采用式(13),参数取值仍为α=[1],Γ=[0.8 0 1.2 -0.09],L=[0.8 0 1.2 0],仍满足收敛条件。
(1) 当对负载质量m=4 kg的同一批次货物运输时,小车的期望位移仍如图2所示,摆角期望值为零。在每次运行时,初始位移和摆角都为零,小车位移跟踪情况如图5所示。从图中可以看出,k相同时,m=4 kg时小车跟踪到目标位移时所用时间比m=6 kg要短。图6为k=20时负载摆角的跟踪情况。可以看出,当质量较小时,负载摆角的最大值约为0.115 rad,要大于m=6 kg时的摆角最大值。
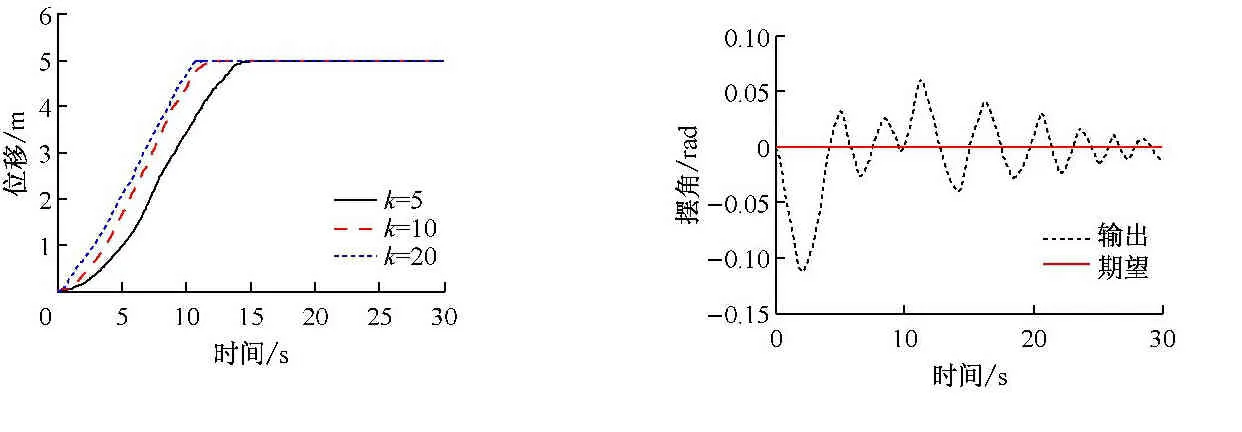
图5 位移跟踪结果 图6 摆角跟踪结果
(2) 当负载质量m=8 kg,小车的期望位移仍如图2所示,摆角期望值为零。小车的初始位移为零,初始摆角为零。小车位移跟踪情况如图7所示。从图中可以看出,相同次数下,m=8 kg时小车跟踪到目标位移时所用时间比m=6 kg要长。图8所示为k=20时负载摆角的跟踪情况。可以看出,当质量较大时,负载摆角的最大值约为70 mrad,要小于m=6 kg时的摆角最大值。
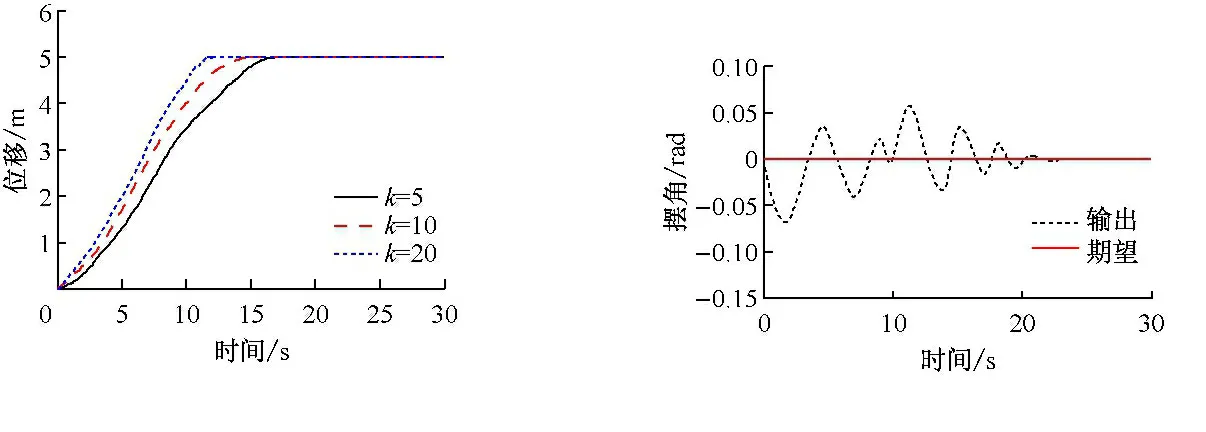
图7 位移跟踪结果 图8 摆角跟踪结果
5 结 语
针对桥式起重机在运行时做重复性运动的性质,首先根据拉格朗日方程推导出动力学微分方程,并对微分方程进行线性化处理,设计了迭代学习控制算法,验证所设计算法的收敛性。结果表明,迭代学习控制可以利用上次的运行信息对下次的输入进行调整,通过对不理想的信号进行改进,产生更加精准的控制信号来提高桥式起重机的跟踪性能,为桥式起重机精确定位,防摇控制提供了科学依据。
[1] 朱发渊,汪朝晖,李欣欣. 桥式起重机定位和消摆的非线性优化 PID 控制研究[J]. 制造业自动化,2014,36(24):76-79.
[2] 孙 宁. 欠驱动吊车轨迹规划与非线性控制策略设计、分析及应用[D]. 天津:南开大学,2014.
[3] 欧阳慧珉,张广明,王德明,等. 基于S型曲线轨道的桥式起重机最优控制[J]. 振动与冲击,2014,33(23):140-144.
[4] Sun N,Fang Y,Zhang Y,etal.A noval kinematic couping-based trajectory planning method for ovehead cranes[J].IEEE/ASME Transactions on Mechatronics,2012,17(1):166-173.
[5] Solihin M I, Legowo A, Akmeliawati R. Robust PID anti-swing control of automatic gantry crane based on Kharitonov’s stability[C]//Industrial Electronics and Applications, 2009. ICIEA 2009. 4th IEEE Conference on. IEEE,2009:275-280.
[6] Antic D, Jovanovic Z, Peric S, et al. Anti-swing fuzzy controller applied in a 3D crane system[J]. Engineering, Technology & Applied Science Research, 2012, 2(2): 196-200.
[7] 游 谊, 张自强, 董 燕, 等. 基于模糊控制的塔式起重机定位和防摆仿真实验[J]. 实验室研究与探索, 2013 (2): 81-83.
[8] Nakazono K, Ohnishi K, Kinjo H,etal. Load swing suppression for rotary crane using neuro-controller optimized by genetic algorithm[J]. IEEJ Transactions on Electronics, Information and Systems, 2010, 130: 889-894.
[9] 杨春燕. 桥式起重机定位和防摆的 RBF 神经网络控制[J]. 中国科技论文在线, 2011, 6(4): 320-324.
[10] Ruan X, Bien Z Z, Wang Q. Convergence characteristics of proportional-type iterative learning control in the sense of Lebesgue-p norm[J]. Control Theory & Applications, IET, 2012, 6(5): 707-714.
[11] 刘国荣, 张扬名. 移动机器人轨迹跟踪的模糊 PID-P 型迭代学习控制[J]. 电子学报, 2013, 41(8): 1536-1541.
[12] 李伟. 起重机载荷摆震模型的简化条件及误差[J].山东建筑工程学报,1998,13(2):59-64.
[13] Lee Ho-Hoon. Modeling and control a three-dimensional overhead crane[J]. Journal of Dynamic Systems (Measurement and Control), 1998(10):471-476.
[14] 谢胜利,田森平,谢振东.迭代学习控制的理论与应用[M].北京:科学出版社,2005.
[15] 李星毅,绪 远,王 轶.改进的时不变系统 PD 型迭代学习控制算法[J].计算机工程与应用,2008,44(31):75-77.
The Position Tracking and Anti-swing for Bridge Crane Based on Iterative Learning Control
FUZiyi1,YUANHaiguo1,2,WANGYilong1
(1. School of Electrical Engineering and Automation, Henan Polytechnic University, Jiaozuo 454003, Henan, China; 2. Zhengzhou Electric Power College, Zhengzhou 450000, China)
In the trolley traveling, load swing may influence work efficiency and cause accidents easily, losing efficacy of optimal control law of a bridge crane. Iterative learning control was put forward to research the position and anti-swing controls of bridge crane. The mathematical model of bridge crane was built with Lagrange equation, positioning anti-swing simulation for bridge crane were carried out. The results show that the iterative learning control can implement highly accurate tracking and effectively restrain the swing angle by using the character of repetitive motion of bridge crane.
bridge crane; iterative learning; Lagrange’s equation; positioning and anti-swing; repetitive motion
2016-05-12
河南省科技攻关计划项目(112102210004)
付子义(1958-),男,河南焦作人,教授,博士生导师,主要研究领域为智能信号处理。
Tel.:0391-3987564; E-mail:Fuzy@hpu.edu.cn
TP 391.9
A
1006-7167(2017)02-0034-05
