直线回归中回归系数公式推导的教学研究
2017-04-12武兆云杨慧娟张小全丁永乐杨铁钊
武兆云, 杨慧娟 , 张 丹, 张小全, 丁永乐, 杨铁钊
(1.河南农业大学 烟草学院,河南 郑州 450002; 2.河南农业大学 农学院,河南 郑州 450002)
直线回归中回归系数公式推导的教学研究
武兆云1, 杨慧娟1, 张 丹2, 张小全1, 丁永乐1, 杨铁钊1
(1.河南农业大学 烟草学院,河南 郑州 450002; 2.河南农业大学 农学院,河南 郑州 450002)
回归系数的计算是直线回归的关键一步,而其公式结构复杂,因此掌握其推导过程尤为重要.提出了直线回归中回归系数公式推导的逻辑思路和方法,并提出了教学建议.
直线回归;回归系数公式;回归截距;乘积和;离均差平方和;推导过程
0 引言
直线回归是农业类高等院校生物统计学教学重要的一章,学生应当掌握回归系数和截距的计算.因此,理解和掌握其公式推导过程就显得非常重要.在一些高等院校生物统计教材中[1-2],对其公式的推导过于简单化,其推导过程也存在值得商榷的地方.这样就造成了学生难以掌握公式.为此,本文在这方面进行了一些思考,提出了更符合逻辑思维的推导过程.
1 直线回归方程式回归系数b和回归截距a的推导方法
1.1 回归系数b和回归截距a的定义
设有两个变量x,y的一组观察数据(x1,y1),(x2,y2),…,(xn,yn),其样本容量为n.该组数据在散点图上呈现直线趋势,可用直线回归方程来描述,则方程的一般式为
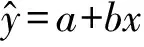
(1)

1.2 回归系数b和回归截距a的计算
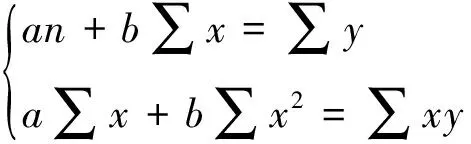
得

(2)
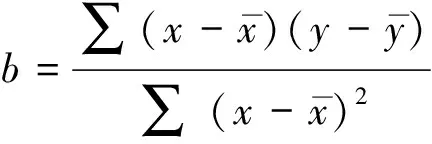
(3)
1.3 回归系数b的推导
式(3)可简写为

(4)
SP表示为乘积和(sum of products),即x的离均差与y的离均差乘积的和,SSx表示为x的离均差平方和.

(5)
而

其中x1,x2,…,xn和y1,y2,…,yn组成了n对观察值(x1,y1),(x2,y2),…,(xn,yn),则

(6)
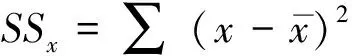
(7)
而
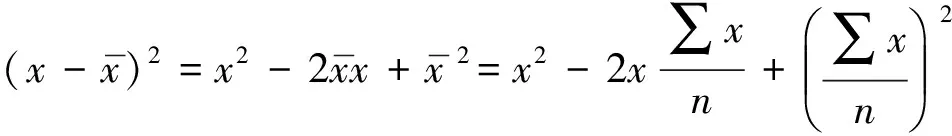
则

(8)
将(8)和(6)代入(3),则

可以将回归系数b推导过程概括为

2 讨论
生物统计学是运用概率论与数理统计的原理及方法来分析解释生物界各种现象和实验调查资料的一门学科,不仅在传统生物学、医学、药学和农学中被广泛应用,而且也是新兴的生物信息学研究中不可缺少的工具[3].生物统计学教学内容上包括试验设计方法和数据分析处理,培养学生如何正确科学地设计试验以及如何正确地收集、整理和分析数据,进而得出客观正确的结论.
该课程的试验设计与数据分析思路抽象,涉及的公式众多,因此学生普遍反映“听不懂”“记不住”“不会用”.这些问题主要表现在对公式的理解和记忆上.我们结合学生的考试情况来看,例如有些学生应用中学数学方法来求解直线回归方程的回归系数和截距,这充分说明学生没有掌握这些复杂的公式.可以看出公式成为该课程的拦路虎.近些年有的教师认为应当减少公式的推导过程[4].教学经验告诉我们放松对公式的推导会出问题的.那些复杂的公式怎样通过简单的推导来使学生充分理解公式的含义以及快速掌握,这同样是该课程的教学重点,教师应当在课前下功夫进行推导.只有学生掌握了公式推导过程,才不会产生畏难情绪,并随之产生学习兴趣.
[1] 赵选民.试验设计方法[M].北京:科学出版社,2006:32-33.
[2] 李云雁,胡传荣.试验设计与数据处理[M].北京:化学工业出版社,2005:44-46.
[3] 李春喜.生物统计学:3[M].北京:科学出版社,2005:1-2.
[4] 李昆太,程新.生物统计学教学改革初探[J].大学教育,2013(7):93-94.
Teaching Research on Formula Deduction of Regression Coefficient in Linear Regression
WU Zhaoyun1, YANG Huijuan1, ZHANG Dan2, ZHANG Xiaoquan1,DING Yongle1, YANG Tiezhao1
(1.CollegeofTobacco,HenanAgriculturalUniversity,Zhengzhou450002,China;2.CollegeofAgriculture,HenanAgriculturalUniversity,Zhengzhou450002,China)
The calculation of regression coefficient is the key step of linear regression. However, its formula structure is complex, so it is very important to master the process of derivation. A linear regression coefficient formula is derived and some teaching suggestions are put forward.
linear regression; regression coefficient formula; regression intercept; sum of products; sum of squares of mean deviation; derivation process
2016-11-04
河南农业大学高等教育科学研究课题(20160308)
武兆云(1982—),男,安徽马鞍山人,河南农业大学烟草学院讲师,博士.
10.3969/j.issn.1007-0834.2017.01.014
G642.0
A
1007-0834(2017)01-0062-02
