用非精确King-werner法求解奇异问题

初元红, 蒋红敬, 郑喜英

(黄河科技学院 信息工程学院，河南 郑州 450063)

用非精确King-werner法求解奇异问题

初元红, 蒋红敬, 郑喜英

(黄河科技学院 信息工程学院，河南 郑州 450063)

科学中很多实际工程问题、生物问题最终转化为求解非线性奇异方程,king-werner法因为收敛阶较高、计算量少,成为求解非线性方程的经典迭代法.但在建模过程中,抽象的数学模型和实际问题之间,总存在一定偏差,因此研究用非精确king-werner法求解非线性方程意义更大.在精确的king-werner法中加入摄动项,用来求解奇异问题,给出了迭代格式的收敛性和渐进收敛速率.

Hilbert空间；非线性方程；非精确king-werner法；奇异问题；收敛速率

0 引言

设F为Hilbert空间H到H的光滑非线性算子，x*为方程F(x)=0的解.当F′(x*)不可逆时，称方程F(x)=0为奇异方程.文献[1-9]中分别给出了Newton等方法求解奇异方程的过程，并给出了渐进收敛率.由于实际问题和数学模型之间存在差异，所以考虑用非精确king-werner法求解非线性方程F(x)=0，其迭代如下：

(1)

其中T(x)=F(x)+β3(x),r(x)=β2(x).在奇异点处不精确king-werner法仍然收敛,且渐进收敛率为0.430.

1 定理及证明

假设F′(x*)为指数为0的Fredholm算子,用N和X表示F′(x*)零空间和值域,用PN和PX表示H到N和X上的投影算子且满足[3]：F′(x*)有一维零空间

N=span{φ}， ‖φ‖=<φ,φ>1/2=1，H=X⊕N，

(2)

PNF″(x*)(φ,φ)≠0，PN=I-PX.

(3)

记

(4)

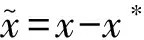
引理1 若F满足下列条件

1) dimN=1； 2)F∈C3； 3)B(z)为N上的可逆算子,∀z∈N,

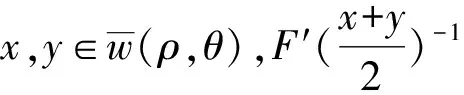
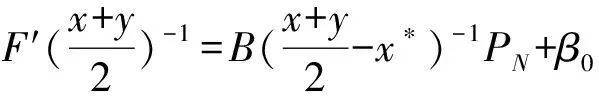
(5)

证明略.

本文的主要结果：

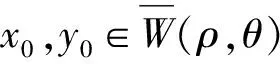
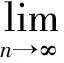
(6)

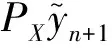
(7)

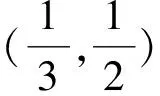
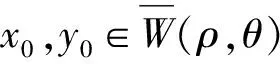
y1-x*=y0-x*-F′(z0)-1(F(y0)+β3(y0))+β2(y0).

(8)

由引理1知

F′(z0)-1=β-1(z0)，

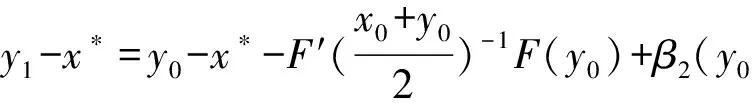
由泰勒公式有

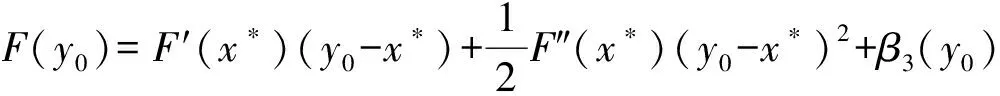
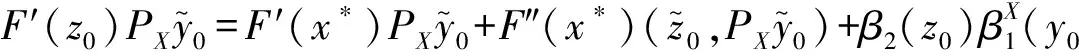
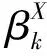
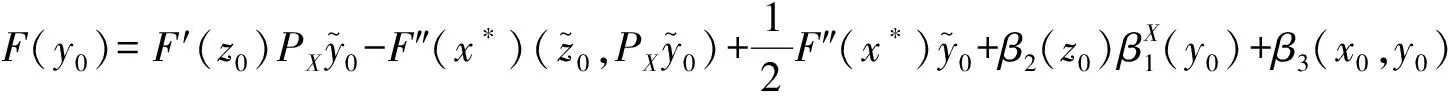
带入(8)得

(9)

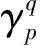
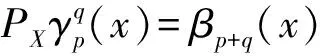
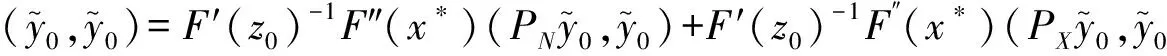
(10)

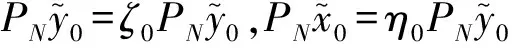
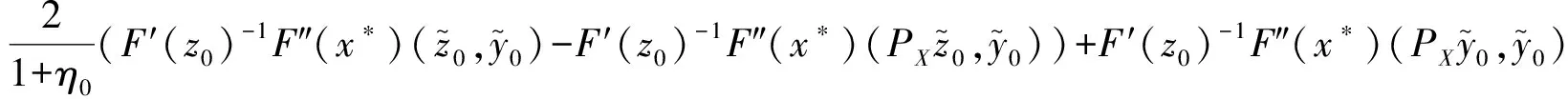
由引理1可知

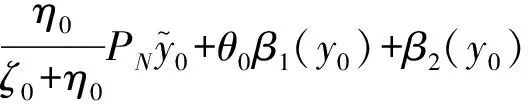
同理,可以推出

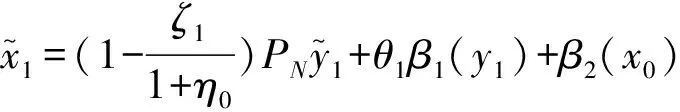
且存在常数c1,c2使

(11)

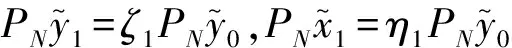
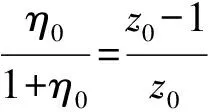
由式(11)有

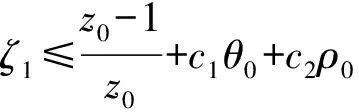
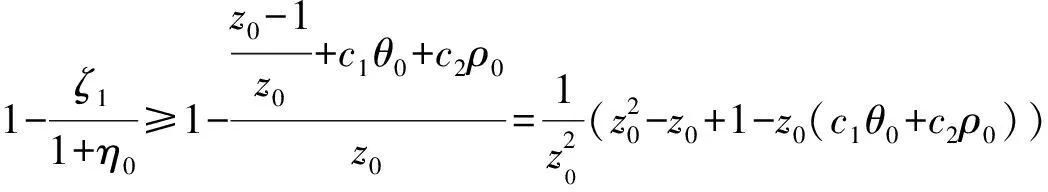
即

取α<1,则有

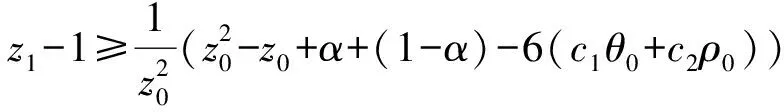
取θ0,ρ0充分小,使(1-α)-6(c1θ0+c2ρ0)≥0,则

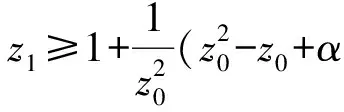
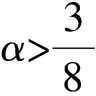
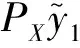
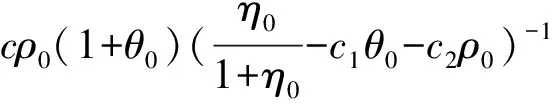
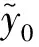
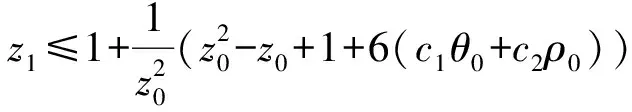
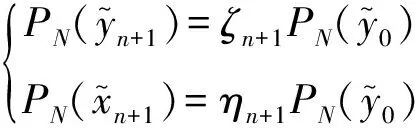
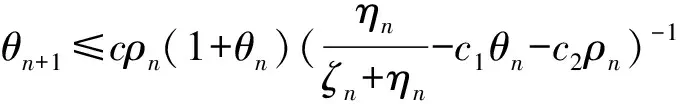
ρn=yn-x*,ζn+ηn=znζn，

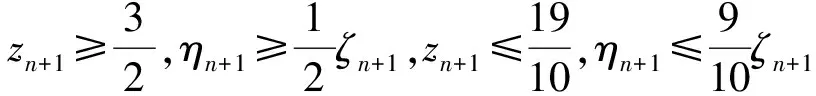
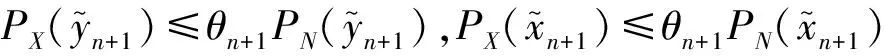
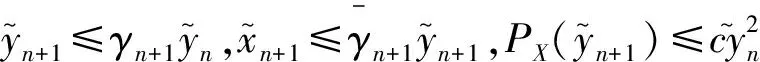
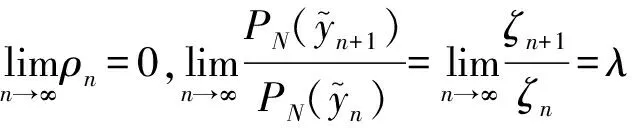
上面证明了非精确king-werner法的收敛性，下面将该方法加速.

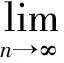
(12)

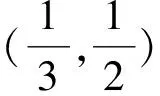
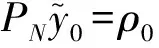
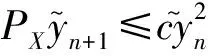
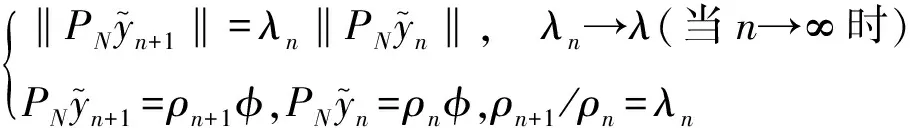
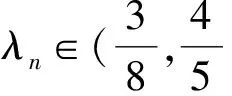
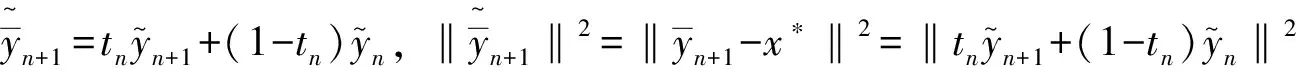
利用Hilbert空间的特征不等式得[9]

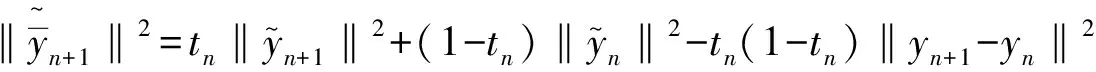
则

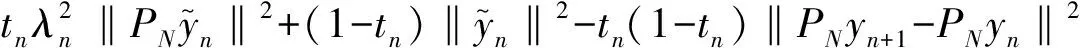
为了提高算法的收敛速率,令

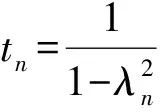
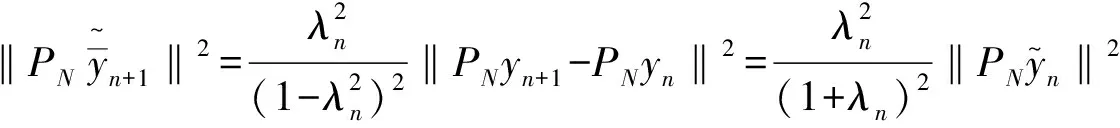
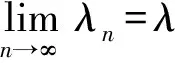
证明略.

2 计算实例

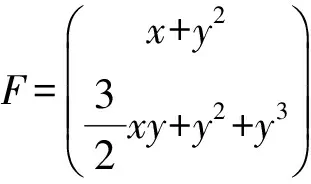
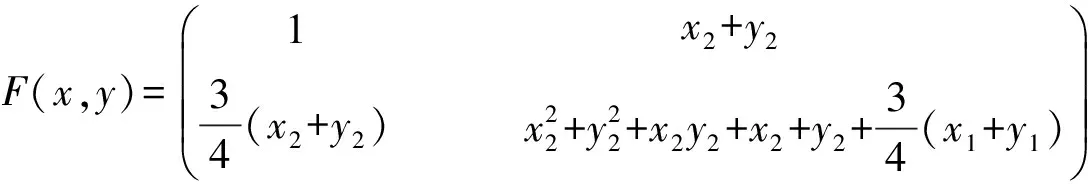
取初始点x1=0.1，x2=0.5，y1=0.12，y2=0.5,部分计算结果见表1.

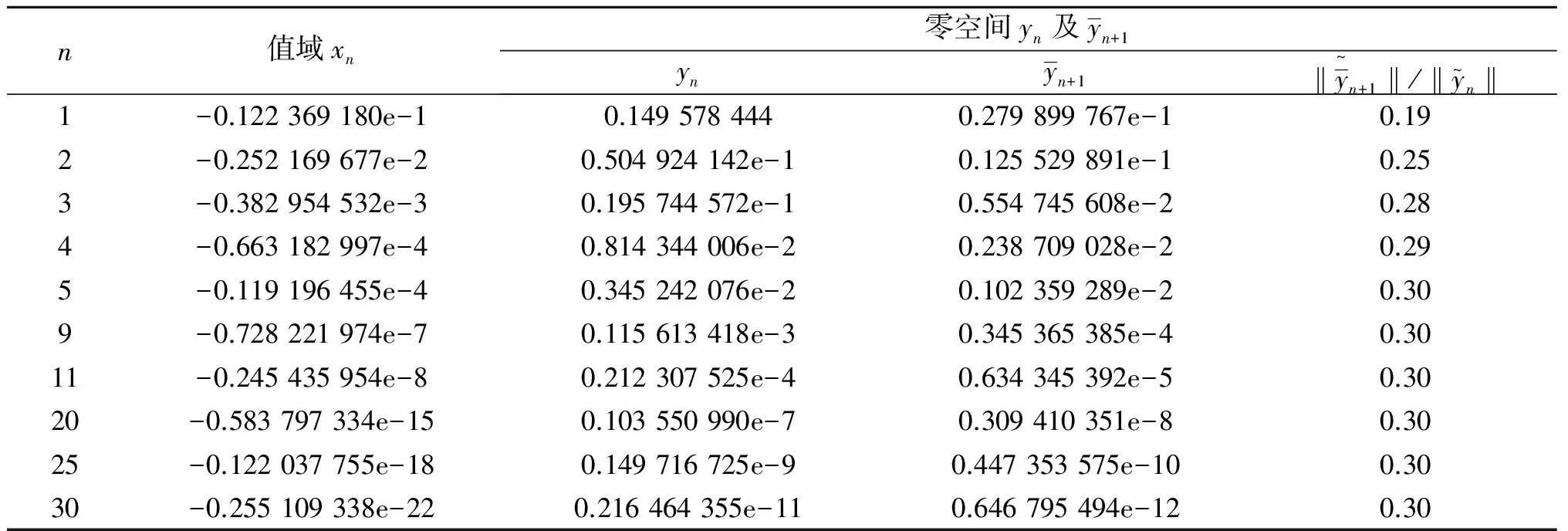
表1 部分计算结果

3 结论

[1] RALL L B. Convergence of the Newton process to multiple solutions[J].Numerische Mathematik,1966,9(1): 23-37.

[2] REDDIEN G W. On Newton’s method for singular problems[J]. SIAM Journal on Numerical Analysis,1978,15(5): 993-996.

[3] DECKER D W,KELLEY C T. Convergence rates for Newton’s method at singular point[J]. SIAM Journal on Numerical Analysis,1983,20(2):296-314.

[4] DECKER D W,KELLEY C T. Convergence acceleration for Newton’s Method at singular point[J]. SIAM Journal on Numerical Analysis, 1982, 19(1): 219-229.

[5] 潘状元.求解奇异问题加速迭代格式的构造[J].工程数学学报,1997,14(2):59-64.

[6] 初元红,潘状元,刘晓敏.用修正的Broyden方法求解奇异问题[J].哈尔滨理工大学学报,2006,11(1):39-42.

[7] 初元红,马红娟.Newton-Moser法在奇异点处的加速[J].数值计算与计算机应用,2014,35(1):53-58.

[8] 杨月梅,潘状元.用非精确的平行割线法求解奇异问题[J].数学的实践与认识,2013,43(6):240-245.

[9] 徐宗本.LP空间特征不等式及应用[J].数学学报,1989,12(2):209-218.

Non-accurate King-werner Method for Solving Singular Problem

CHU Yuanhong, JIANG Hongjing, ZHENG Xiying

(CollegeofInformationEngineering,HuangheScienceandTechnologyCollege,Zhengzhou450063,China)

In science, there are many practical engineering problems and biological problems which have to be transformed into solving nonlinear singular equations. The king-werner method is a classical iterative method for solving nonlinear equations because of its higher convergence order and less computation. But in the process of modeling, there is always a certain deviation between abstract mathematical model and practical problems. So it is important to research the non-accurate king-werner method which is used to solve the nonlinear equation. Adding the perturbation term in the precise king-werner method is used to solve the singular problem. The convergence and the asymptotic convergence rate of the iterative scheme are given.

Hilbert space; nonlinear equation; non-accurate king-werner method; singular problems; convergence rate

2016-12-06

郑州市科技局资助项目(20141374,20141375)；河南省教育厅项目(14B110024)

初元红(1979—),女,河南郑州人,黄河科技学院信息工程学院副教授，主要研究方向:数值计算.

10.3969/j.issn.1007-0834.2017.01.004

O241

A

1007-0834(2017)01-0019-05