二维离散单元法在某旧金属矿改造边坡稳定性研究中的应用

董梦龙，李运胜，李雨坤

（1.河海大学 地球科学与工程学院，江苏 南京 210098；2.浙江省地矿勘察院，浙江 杭州 310013）

二维离散单元法在某旧金属矿改造边坡稳定性研究中的应用

董梦龙1，李运胜2，李雨坤1

（1.河海大学 地球科学与工程学院，江苏 南京 210098；2.浙江省地矿勘察院，浙江 杭州 310013）

金属矿山露天开采后将形成规模较大的边坡，如何处理利用废弃矿山的边坡资源是提高国土资源利用的重要途径。本文以某金属矿山废弃采坑边坡为例，利用二维离散单元法研究其稳定性。该矿山边坡为岩质边坡与松散堆积体（尾矿）的结合体，局部为陡崖和陡坡，工程地质形态复杂。研究选取了2个具有代表性的剖面，分析计算了天然工况、暴雨工况和地震工况下的边坡稳定性，得出相应的稳定系数，并预测了边坡可能发生的失稳模式，并提出了相应的治理意见。研究表明，二维离散单元法能适用于复杂形态下的边坡稳定性分析，并可作为条分法计算的重要补充。

采坑边坡；稳定分析；二维离散单元法

0 引言

边坡在自然界以及人类工程中及其常见，是工程建设中最重要的地质环境之一，也是工程建设中最常见的工程形式。由于人类工程建设活动的不断增加，在矿山、水利、交通以及城建等部门都涉及到大量的边坡问题。我国是一个矿业大国，现有大量的金属矿山采用露天开采，从而形成规模巨大的边坡工程，有的甚至高达300 m以上。而这些金属矿边坡的稳定性问题十分严重，一旦失稳将对生产造成严重影响，并带来巨大的经济损失。近年来金属矿边坡失稳滑坡事故时有发生，例如，本钢南芬露天矿在1999年5月至2002年7月的短短3年时间内，就发生4次近百万方的大型滑坡灾害，造成了数千万元的经济损失；酒泉钢铁公司的黑沟铁矿在其基建期间发生了一次极为严重滑坡和泥石流灾害，该地质灾害直接堵塞了酒泉市、嘉峪关市两市唯一的水源北大河，造成直接经济损失高达4 000余万元；2004年四川省雅安市宝兴县陇东镇宇通矿山的“10·18”特大岩体垮塌事故造成巨大的经济损失和人员伤亡[1-2]。这些事故无一不说明了矿山边坡工程稳定性的重要性。另外，随着一些矿山生产周期结束，废弃露采矿山的综合整治也是提高国土资源利用的重要工程途径。

边坡稳定性分析的方法很多，但总的说来可分为两大类，即以极限平衡理论为基础的条分法和弹塑性理论为基础的数值计算方法，其中离散单元法为现阶段数值分析方法中发展较快的一种。离散单元法是分析离散介质变形和运动趋势的有力工具，自1971年Cundall提出离散单元模型以来，就广泛的应用于各类工程的数值模拟和分析研究中[3]。李作良等采用离散单元法对钨矿采空区进行数值模拟，分析其稳定状况[4]。张国庆等利用UDEC二维离散元软件对倾斜工作面开采导致的覆岩移动及裂隙发育过程进行数值模拟，模拟了开采过程中覆岩移动及裂隙发育规律[5]。

本文以某旧铁矿采坑边坡为例，研究了离散单元法对该类边坡的稳定评价的适用性。

1 工程概况

1.1 工程简介

某景区拟利用某旧铁矿的采坑进行改造修建景区建筑物（图1），达到废弃矿山综合改造，提高土地资源利用的目的。拟利用的采坑深约30 m，采坑顶部至周边山体顶部高差30～100 m，采坑底部至周边山体的顶部高差60～130 m不等，坡度在20°～45°之间，岩层局部直立后反倾，该边坡的稳定性与项目主体建筑及附属设施的安全直接相关，所以对该边坡工程进行稳定性分析和评价是十分必要，而且具有重要的工程意义。

图1 旧铁矿采坑全景图Fig.1 Panoramic view of the old iron ore pit

1.2 区域地质构造

根据研究区域的区域地质资料，所研究的旧铁矿边坡位于扬子准地台下扬子台褶带，区域构造带属淮阳山字形反射弧之西段。区域内的构造运动主要受燕山-喜马拉雅运动的影响。燕山构造期内使得区域内的褶皱活动和断层的升降活动剧烈；而喜马拉雅期内的构造运动相对较弱，对区域内的构造影响相对较小。所以研究区域内主要的构造运动为褶皱与断层。

1.3 地层岩性

研究区域内地层属宁芜地层小区北部，以中生代侏罗系地层分布为主。出露地层的岩性主要为侏罗系中风化至全强风化凝灰岩和第四系松散堆积层，上覆第四系主要以人工填土层（Q4ml）及坡积层（Q3dl）。

1.4 边坡现状

研究区域东西两侧的最高海拔标高约247.5 m与201.6 m，中部为连接两峰的鞍形山脊，后鞍形山脊处开山采石，形成了南北长约462 m，东西宽约294 m的采矿坑，坑底高程在110 m，南北两侧高程在160～170 m之间，采坑四周均为坡度较陡的山坡。由此形成高约50～130 m不等的高边坡，坡度平均在35°左右，局部直立或反倾。

矿坑西侧、北侧和矿坑南部高平台西南侧和东南侧共有五个尾矿渣堆积体。由尾矿渣堆积而成，厚度在5～35 m，土质不均，颗粒成分从黏性土到漂石均有，结构从松散到致密不均，渗透性好。矿坑南侧高平台高程在157～163 m之间，呈南北向长条形状，面积9 000 m2。局部尾矿渣堆积体有变形迹象。

所以该研究边坡为岩质边坡和矿渣堆积体相结合的边坡，局部为开矿形成的陡崖和陡坡，离散状态的坡体体尤其适合离散单元法分析稳定状况。

工程地质平面图见图2。

图2 工程地质平面图Fig.2 Engineering geological plan

2 计算原理与软件介绍

离散元方法针对由不同的小块体所构成的整体进行应力、应变的分析计算，而对于各不同块体之间的连接是通过接触点的耦合的模拟而互相连接在一起。对于岩体这一特殊的材料体分析，其主要的组成部分为岩石和结构面两大部分。而岩体中的结构面的刚度和强度相比于岩石本身的强度要小得多。考虑到岩体这一特殊性质，通常将岩体中的岩石假定为刚性体以减少不确定性（自由度）的数量，所以岩体产生的变形主要为岩体中结构面的总位移所产生，而结构面的位移是由各接触点（面）的变形所引起[6-8]。

对于岩体的研究是将其假定为各种离散块体的堆砌，而这些块体之间的相互作用力是根据位移和力的关系式来求解，其中每一个块体的运动都遵循牛顿运动的基本定律—即力和力矩的平衡定律。三大方程（平衡方程、变形协调方程和本构方程）是数值分析模型的建立的基础，模型同时还必须满足相应的边界条件。而离散元单个块体之间是不存在相互的变形约束，每个块体仅需要满足的是以下的物理方程和运动方程。

2.1 物理方程

离散单元法的物理方程是表述力与位移之间的相互关系。块体之间的力的法向分力为Fn与它们之间的法向位移量Sn为正比关系，即：

式中：系数Kn为法向刚度系数。

块体之间的力切向的分量Ft与切向的相对位移量St的关系：

式中：系数Kt为接触面的切向刚度系数[5-6]。

2.2 运动方程

对应块体所受的一组力F1，…，Fn，产生合力F合和合力距M，由牛顿第二运动定律确定该块体的加速度和角速度，然后可以确定时间步长Δt内的速度和角速度以及位移和转动量。

式中：a为加速度，m为岩块的质量。

上式应该理解为分别对X方向和Y方向求加速度。然后分别进行向前差分的数值积分，可以得到岩块X方向和Y方向的速度和位移：

式中：V（t1）为t1时间的速度；U（t1）为t1时间的位移，t0为起始时间，Δt为时间步长。

计算时依据时步迭代并遍历每个块体，直到每个块体不再出现不平衡力和不平衡力矩为止。

离散单元法区别于其他数值方法的主要特征是：（1）它能反映块体之间接触面的滑移、分离和翻转等不连续变形，还能计算块体内部的变形和应力分布状态。（2）可以用于求解非线性大位移和动力稳定问题，这一应用是根据显示时间差分解法来求解动力平衡方程[9]。

2.3 软件介绍

UDEC（Universal Distinct Element Code）是由美国Itasca软件公司开发的，是在离散单元法基础上编制的通用的离散元程序。UDEC将不连续介质视为离散块体的集合，不连续性则看作块体之间的边界条件。本文主要采用针对非连续介质模拟的离散元数值计算程序UDEC4.0。

3 数值建模

3.1 计算工况

结合坡体特征与坡体所处地质环境，该边坡稳定性计算工况见表1。根据工程区气候资料，区内雨量充沛，年降水1 200 mm，年平均降水量1 106 mm，降水最多季节为7月份，494.5 mm，最少为2月份，仅7.7 mm。所以暴雨工况下降水量计算值取160 mm/d。根据工程区地震资料，边坡设计地震加速度值取0.10 g。

表1 边坡稳定性计算工况Tab.1 Slope stability calculation

3.2 计算参数

强度参数的选取合理与否，对边坡稳定性计算起关键性作用。边坡失稳形成后，在新的环境条件下，结构遭到破坏、抗剪强度降低至残余强度的滑带土，在上覆滑体自重应力作用下发生压密，其残余强度有一定的恢复特性；而在暴雨工况下，滑体土通常并不能达到饱和，对滑带土的软化作用也往往不会完全达到饱和软化的程度。根据滑带土室内试验结果，综合考虑边坡失稳时的土体状态，以天然和饱和状态下的峰值和残余强度试验值为基础综合选取。

（1）自然工况下，滑动面抗剪强度参数以滑带土天然状态抗剪峰值强度与残余强度之间取值，接近于峰值强度；

（2）暴雨工况下，考虑到滑动面岩土一般并不会达到饱和，抗剪强度参数以滑带土饱和状态抗剪峰值强度与残余强度之间、接近于残余强度取值；

（3）当计算滑动面位于滑体土内时，自然、暴雨工况下，抗剪强度参数分别以滑体土天然和饱和抗剪强度计算；当计算滑动面沿滑带土和部分穿越滑体土时，分段计算。

根据该边坡的工程地质详细勘察报告，结合岩体力学参数实验，计算模型所选取的岩土体物理力学参数和结构面力学参数见表2和表3。

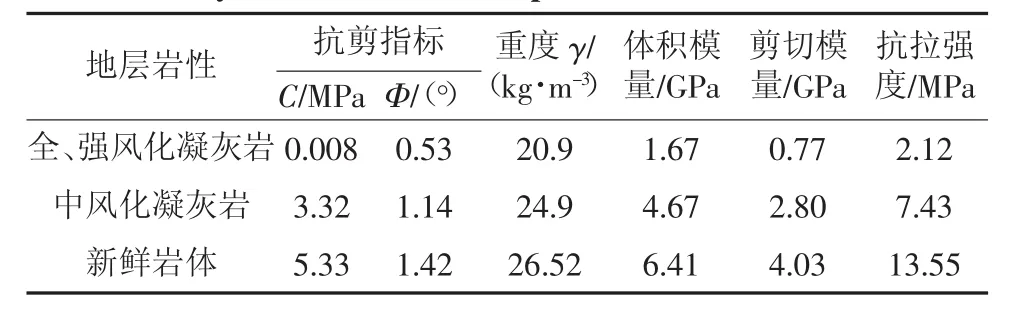
表2 不同岩层物理力学参数取值Tab.2 Physical and mechanical parameters of different strata

表3 结构面物理力学参数取值Tab.3 Physical and mechanical parameters of structural plane

3.3 计算模型

对该工程实例的二维离散元稳定性分析主要是针对该矿坑的南部废石堆积体和北部废石堆积体，见图2，所以计算选取了该边坡具有代表性的剖面3-3'、6-6'。

图3为DP3-3'剖面。由图3可见，坡表主要由残坡积土和全、强风化凝灰岩组成，下覆基岩为凝灰岩。岩石受通过场区的两条构造影响，节理裂隙发育，主要方向为NNE向、NE向、NWW向，上述节理裂隙延伸长度较长，除NNW倾角较小外，其余各节理裂隙倾角均较陡。边坡的浅表层，岩石的表面张性裂隙发育，局部直立或反倾。

根据DP3-3'剖面资料，建立相应数值模型。根据岩体风化程度，模型所选取岩体材料主要有全强风化凝灰岩、中风化凝灰岩和新鲜凝灰岩三类。具体岩土体材料参数见表2。根据所模拟岩土体特性，模型所采用本构模型为摩尔-库伦破坏模型。模型中设置结构面主要考虑有层面和非层面两类结构面。结构面参数见表3。结构面同样采用摩尔-库伦破坏模型。模型尺寸高100 m，宽150 m；共划分block 287个，zone 2 976个。模型底部、正面与背面边界条件设置为固定位移边界（即zero-velocity boundary）以控制模型底部与正面、背面的变形。顶部设置为自由边界（即free boundary）。垂直方向初始地应力由岩土体自身重力决定；设置两方向水平初始地应力为垂直向的一半。具体计算模型见图4。计算中迭代至不平衡力趋近于0，该模型中设置迭代至不平衡力的数量级达到10-5。

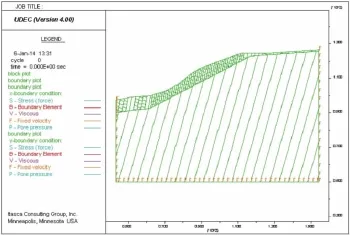
图4 DP3-3'剖面离散元计算模型Fig.4 DP3-3'discrete element model

图5为DP6-6'剖面，坡表主要由残坡积土和全、强风化凝灰岩组成，下覆基岩为凝灰岩。岩石受通过场区的两条构造影响，节理裂隙发育，主要方向为NNE向、NE向、NWW向，上述节理裂隙延伸长度较长，除NNW倾角较小外，其余各节理裂隙倾角均较陡。边坡的浅表层，岩石的表面张性裂隙发育，局部直立或反倾。

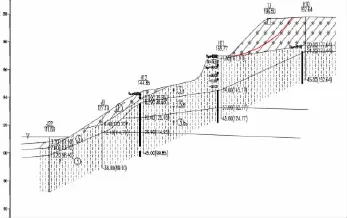
图5 边坡计算剖面DP6-6'Fig.5 Slope calculation section DP6-6'

根据DP6-6'剖面资料，建立相应数值模型。根据岩体风化程度，模型所选取岩体材料主要有全强风化凝灰岩和新鲜凝灰岩两类。具体岩土体材料参数见表2。根据所模拟岩土体特性，模型所采用本构模型为摩尔-库伦破坏模型。模型中设置结构面主要考虑有层面和非层面的结构面两类。结构面参数见表3。结构面同样采用摩尔-库伦破坏模型。模型尺寸高135 m，宽195 m；共划分block 372个，zone 3 615个。其他设置与DP3-3'剖面相同。具体计算模型见图6。

图6 DP6-6'剖面离散元计算模型Fig.6 DP6-6'discrete element model

4 结果分析

4.1 DP3-3'剖面计算结果分析

DP3-3'剖面在天然工况、暴雨工况（160 mm/d）和地震工况（水平加速度系数为0.1）下，边坡稳定性计算结果见图7、图8、图9。

计算结果表明DP3-3'剖面潜在滑动面位于边坡中部，全、强风化凝灰岩与基岩分界面，水平埋深约9 m，竖直方向埋深约6 m。天然工况下，边坡的稳定系数为1.10，边坡岩土体的最大位移约8 cm，边坡整体稳定性较好，不会发生滑动破坏。暴雨工况下，边坡的稳定系数为0.93，边坡稳定性差，极易发生滑坡。地震工况下，边坡的稳定系数为1.01，边坡处于极限平衡状态，考虑到边坡表层岩体大量发育有风化裂隙、爆破裂隙等，边坡易发生局部崩塌、块体掉落等灾害。

图7 天然工况下局部失稳矢量图Fig.7 Local instability vector diagram under natural condition

图8 暴雨工况局部失稳矢量图Fig.8 Local instability vector diagram under rainstorm condition

图9 地震工况下局部失稳矢量图Fig.9 Local instability vector under seismic condition

4.2 DP6-6'剖面计算结果分析

DP6-6'剖面在天然工况、暴雨工况（160 mm/d）和地震工况（水平加速度系数为0.1）下，边坡稳定性计算结果见图10、图11、图12。

图10 天然工况下局部失稳矢量图Fig.10 Local instability vector diagram under natural condition

图11 暴雨工况下局部失稳矢量图Fig.11 Local instability vector diagram under rainstorm condition

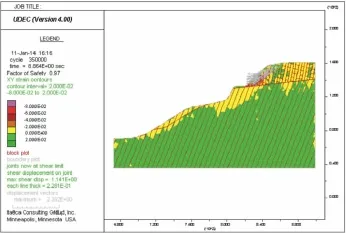
图12 地震工况下局部失稳矢量图Fig.12 Local instability vector under seismic condition

计算结果表明，DP6-6'剖面的潜在失稳区域集中在边坡顶部，潜在滑动面的埋深约15 m。天然状况下，边坡的稳定系数为1.08，边坡整体稳定，不会发生破坏。在暴雨条件下，由于雨水的入渗产生的向坡外的渗流力以及降水导致的岩土体力学参数的降低，边坡稳定性变差，稳定系数为0.92，可能发生滑动破坏。地震工况下，边坡的稳定系数为0.97，边坡处于极限平衡状态，易发生倾倒、崩塌等地质灾害。

4.3与条分法计算结果比较

根据有关边坡工程技术规范[10-11]，研究同时采用摩根斯坦-普赖斯法（Mogenstem-price）和毕肖普法（Bishop）对两个剖面进行稳定性分析，用来验证离散单元法对该类边坡分析的合理性。计算结果见表4和表5。

表4 DP3-3'剖面不同计算方法稳定系数比较Tab.4 Comparison of stability coefficient at DP3-3'profile

表5 DP6-6'剖面不同计算方法稳定系数比较Tab.5 Comparison of stability coefficient at DP6-6'profile

通过计算结果比较表明，二维离散单元法得出的边坡稳定系数与二维极限平衡计算结果相近，说明离散单元法对该类边坡的稳定分析是合理的、适用的、也是更严格的。

根据计算结果和不同的失稳模式为边坡治理方案提供了依据。

5 结语

本文简要介绍了二维离散单元法，并将该方法运用到旧金属矿废矿边坡稳定分析这一工程实际问题上。通过2个典型剖面的离散元法稳定性计算分析，得出稳定系数，并预测了边坡可能发生的失稳模式，解决了实际工程问题。可见二维离散单元法对于旧金属矿边坡的稳定评价是适用的、可行的，这对目前很多旧金属矿的二次开发利用具有一定的工程指导意义。

[1] 金属非金属矿山露天矿边坡调查报告[R].马鞍山矿山研究院，2006.12. Investigation report of open pit slope in metal and nonmetal mines [R].Sinosteel Maanshan Institute of Mining Research Co.，2006.12.

[2] 程东幸，刘大安.中国典型重大边坡工程稳定性与安全评价现状研究[J].西部探工，2008（12）：33-37. CHEN Dongxing，LIU Daan.Studyon stability and safety evaluation of typical slope engineering in China [J].Western Exploration，2008（12）：33-37.

[3] Cundall PA（1988）Formulation of a three-dimensional distinct element model-Part 1.A scheme to detect and represent contacts in a system composed of many polyhedral blocks[J].Int J Rock Mech Min Sci&Geomech Abstr.，25：107-116.

[4] 李作良，李一帆.某钨矿采空区稳定性的离散元数值模拟[J].中国钨业，2008，23（6）：1-4. LI Zuoliang，LI Yifan.Discrete element numerical simulation of stability in tungsten mine stope [J].China Tungsten Industry，2008，23（6）：1-4.

[5] 张国庆，黄 霆.某矿UDEC数值模拟研究[J].煤，2010，19（6）：21-23. ZHANG Guoqing，HUANG Ting.Study of numerical simulation on UDEC in one mine[J].Coal，2010，19（6）：21-23.

[6] FALLS S D，YOUNG R P.Acoustic emission and ultrasonic-velocity methods used to characterize the excavation disturbance associated with deep tunnels in hard rock [J].Tectonophysics，1998：178-181.

[7] SHENG Q，YUE Z Q，LEE C F.Estimating the excavation disturbed zone in the permanent shiplock slopes of the Three Gorges Project China[J].International Journal of Rock Mechanics &Mining Sciences，2002：86-89.

[8] GRIFFITHS DV，LANE PA.Slope stability analysis by finite elements[J].Geotechnique，1999：209-215.

[9] BROWN E T，HOEK E.Trends in relationships between measured in-situ stress and depth[J].Int.J.Rock Mech.Min.Sci.&Geomech. Abstr，1978（15）：211-215.

[10] 重庆市设计院.建筑边坡工程设计规范[S].GB50330—2013.北京：中国建筑工业出版社，2014.

[11]水利部水利水电规划设计总院.水利水电工程边坡设计规范[S].北京：中国水利水电出版社，2009.

Application of Two Dimensional Discrete Element Method to the Slope Stability Analysis of an Exhausted Metallic Mine

DONG Menglong1,LI Yunsheng2,LI Yukun1
(1.School of Earth Sciences and Engineering,Hohai University,Nanjing 210098,Jiangsu,China;2.Zhejiang Geological Survey,Hangzhou 310013,Zhejiang, China)

The recycle of slope resources in the exhausted metallic mines is an important way to improve the use of land resources.This paper studies the stability of the abandoned slope in metallic mine by applying two-dimensional discrete element method.The mine slope is a combination of rock slope and loose accumulation body(tailings)with complex engineering geological form.After choosing two representative profiles,we calculate the corresponding slope stability coefficients under the conditions of norm,rainstorm and earthquake.The potential slope instability modes and corresponding treatment technologies are predicted.The results show that the two-dimensional discrete element method,as an important supplement to the calculation of strip method,can be applied to the stability analysis of slope under complex form.

metallic mine slope;stability analysis;two dimensional discrete element method

TD22；P642

A

10.3969/j.issn.1009－0622.2017.01.006

2017-01-11

董梦龙（1988-），男，安徽滁州人，博士研究生，主要从事岩体结构与工程稳定研究。