一种可用于莱斯衰落信道的信噪比估计算法

陈 萍 熊蔚明

(1中国科学院国家空间科学中心, 北京 100190)(2中国科学院大学, 北京 100049)(3中国船舶工业系统工程研究院, 北京 100094)

一种可用于莱斯衰落信道的信噪比估计算法

陈 萍1,2,3熊蔚明1

(1中国科学院国家空间科学中心, 北京 100190)(2中国科学院大学, 北京 100049)(3中国船舶工业系统工程研究院, 北京 100094)

针对莱斯衰落信道条件下,常规非数据辅助信噪比估计算法复杂度高、适用调制类型单一等问题,提出了一种信噪比估计算法.在建立系统等效模型的基础上,推导出信噪比与接收信号期望和方差的关系表达式.由于在莱斯衰落信道下,该表达式无解析解,故提出用多项式拟合法得到一定范围内的信噪比近似解.仿真和对比分析实验表明,提出的信噪比估计算法不需要使用训练序列,不仅对低阶和高阶多种调制方式具有普适性,而且当信道莱斯因子K=10 dB且信噪比为5～25 dB时,归一化估计偏差均小于0.2,计算时间复杂度与M2M4算法相当,适合一般工程应用需要.

信噪比估计;莱斯衰落信道;多项式拟合;非数据辅助

信噪比是衡量通信质量的重要指标,也是无线通信技术的研究热点之一.由于信号在传输过程中受到复杂传播环境的影响,因此需要针对不同应用场景设计高效的信噪比估计方法[1].目前,对于SNR的估计方法主要分为2类:一类为基于数据辅助(data-aided,DA)的方法,另一类则不需要数据辅助(non-data-aided,NDA).NDA 类算法包括最大似然类算法[2]、矩估计类算法[3-4]、子空间类算法[5]等.NDA类算法无需训练序列,因而被广泛应用.

根据样本选取的差异,NDA类信噪比估计算法可以分为:判决域和非判决域的信噪比估计[6].判决域的信噪比估计是指用于估计的信号样本已经经过了同步和均衡操作,其调制方式已知.非判决域的信噪比估计指信号未进行同步和均衡处理(如中频信号),其调制方式未知.

针对高斯白噪声(AWGN)信道,许多学者对信噪比估计方法开展了深入研究.经典信噪比估计算法有最大似然(ML)估计、信号噪声方差(SNV)估计、分离符号矩估计(SSME)、二阶-四阶矩估计(M2M4)以及信号-变换比估计(SVR)算法等.Pauluzzi等[7]利用均方误差(MSE)对上述5种估计方法进行了详细的分析和比较,并通过与克拉美罗界(CRB)[8]的比较,得出了M2M4算法、SNV算法和ML算法有较好估计效果的结论.

在莱斯衰落信道下,由于存在乘性衰落因子,信噪比估计方法一般比在AWGN信道中更复杂.在准静态平坦衰落信道下,对于恒幅调制信号,矩估计器(如M2M4估计器)可以用于衰落信号信噪比估计[9].针对移动通信中广泛使用的 Nakagami-m信道,Ramesh等[10]给出了一种莱斯衰落信道信噪比估计方法.但这种估计方法只考虑了BPSK调制,无法应用于高阶调制.杨俊等[11]主要针对QPSK提出改进的信噪比估计方法.韩博等[12]提出了一种基于相关向量机的信噪比估计方法,该方法应用相关向量机建立估计模型,通过训练学习得到可靠的模型权值.但是该方法需要进行矩阵求逆运算,复杂度较高,不适用于硬件实现.李晋等[13]提出了一种低复杂度盲信噪比估计方法,但是该方法只针对瑞利(Rayleigh)衰落信道进行了分析,没有针对莱斯衰落信道提出信噪比估计方法.

本文从工程应用的角度出发,针对莱斯衰落信道提出一种属于判决域的非数据辅助信噪比估计方法.该方法具有估计精度高、适用范围宽、计算复杂度低的特点,适用于低阶和高阶多种调制信号的信噪比估计.

1 信噪比估计模型

在AWGN信道下,信号输入判决器基本消除了载波偏差和码间干扰,仅混有加性高斯白噪声信号,接收信号rk可表示为

rk=xk+nkk=1,2,…,L

(1)

对于莱斯衰落信道,需改进上述信号模型.设tn为信号源,dk为采样后信号,mk为经过成形滤波器后的信号.ri为信道功率因子(对于莱斯衰落信道,信道增益ri服从莱斯分布),ni为噪声信号,si为接收信号,sk为经过匹配滤波器的信号,信噪比估计的系统等效模型如图1所示[14].在本文的分析中,假设系统均衡和同步误差足够小,不会对信噪比估计造成明显影响.

图1 系统等效模型

过采样和脉冲成形后的信号可表示为

(2)

式中,hk-n为成形滤波器系数;dk为过采样后的信号.则接收信号表示为

si=rimk+ni

(3)

匹配滤波器输出信号为

(4)

则信噪比SNR表示为

(5)

可见,信噪比SNR估计的关键是对式(5)中接收信号功率以及噪声信号方差进行准确估计.

2 莱斯信道信噪比估计算法

2.1 估计算法原理

根据图1所示的系统等效模型,假设用于估计的信号样本经过同步和均衡操作,而且其调制方式已知.设Es为发送符号的能量,接收信号si表示为

(6)

式中,ni与衰落因子ri为相互独立的随机变量.ri服从莱斯分布,表示为[15]

(7)

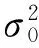
(8)

莱斯因子K可以表示信道的衰落程度,K越大，信道条件越好；反之，则表示多径衰落越严重.K=∞时表示信道条件近似为理想高斯信道,K=0时表示信道条件多径影响严重,可近似认为瑞利信道.可见,瑞利信道是莱斯信道的一种特例.莱斯信道中信号的包络服从莱斯分布,其概率密度函数为

(9)

(10)

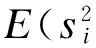
(11)

考虑到衰落因子ri和信道噪声ni为相互独立的随机变量,故E(rini)=E(ri)E(ni)=0,从而,式(11)改写为

(12)

(13)

对于莱斯衰落信道,有

(14)

(15)

(16)

故信噪比表示为

(17)

(18)

(19)

从工程应用角度出发,在保证一定精度的前提下,为降低运算复杂度,本文采用三阶拟合系数.

2.2 估计算法

① 设接收端收到I路和Q路N个数据分别为Ii和Qi.

② 根据下式计算接收数据的幅值Ai和相位φi:

(20)

(21)

③ 按照调制阶数和划分区间的准则将接收到的数据划分为M个区间.

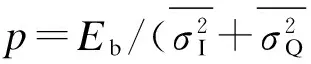
⑧ 对接收数据进行多项式拟合,以p为自变量,理论信噪比γ为应变量,得到拟合多项式f(p),则信噪比估计近似结果γfit=f(p).

上述步骤③中,针对不同的调制方式应用如下准则划分区间:

1) QPSK调制.区间1为0≤φi<π/2;区间2为π/2≤φi<π;区间3为π≤φi<3π/2;区间4为3π/2≤φi<2π.

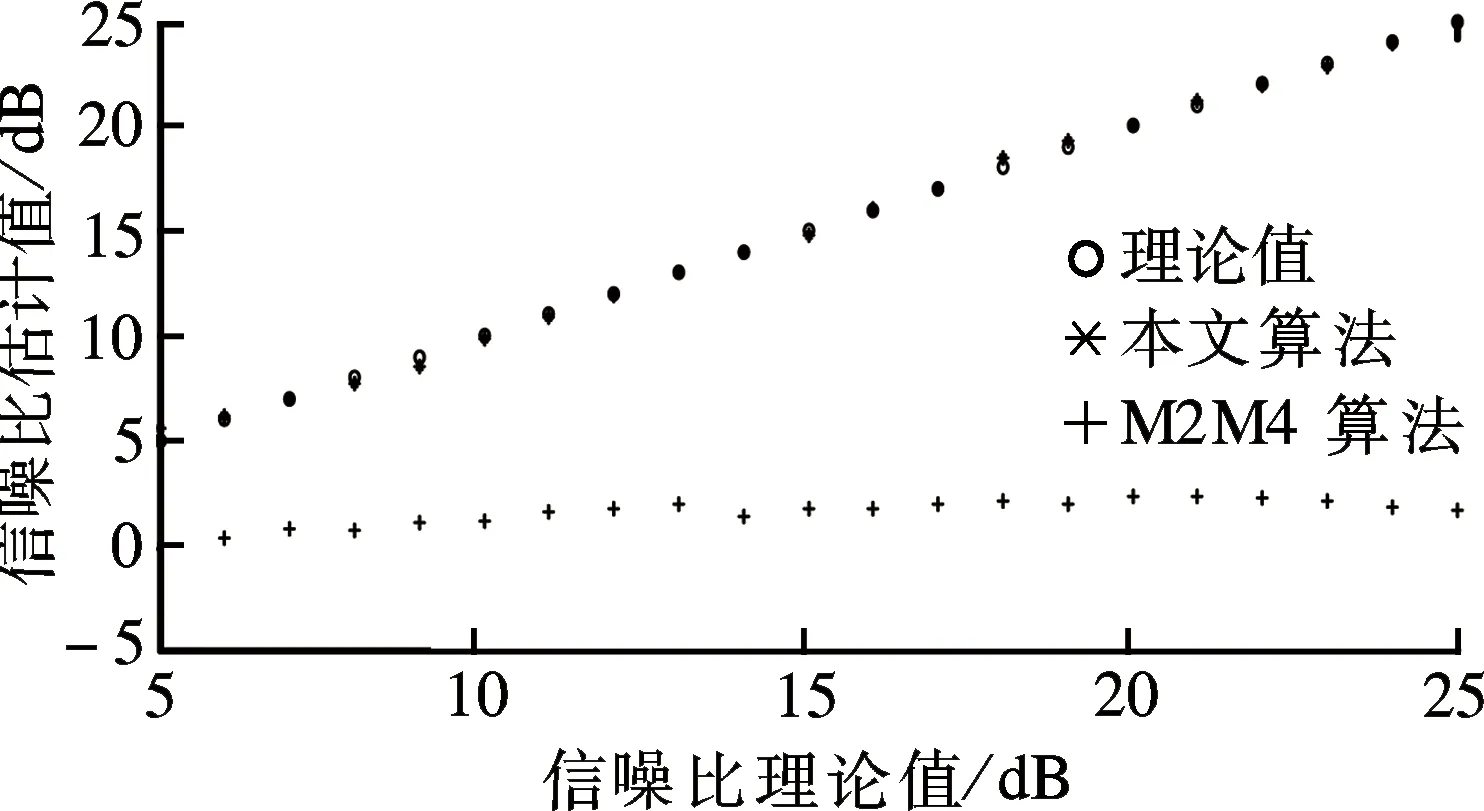
2) 8PSK调制.区间1为0≤φi<π/8或15π/8≤φi<2π;区间2～区间8为mπ/4-π/8≤φi

3) 16APSK调制.区间1为Ai<(Rin+Rout)/2,0≤φi<π/4或7π/4≤φi<2π;区间2～区间4为Ai<(Rin+Rout)/2,mπ/2-π/4≤φi

4) 32APSK调制.区间1为Ai<(Rin+Rmid)/2,0≤φi<π/4或7π/4≤φi<2π;区间2～区间4为Ai<(Rin+Rmid)/2,mπ/2-π/4≤φi(Rout+Rmid)/2,0≤φi<π/16或31π/16≤φi<2π;区间6～区间20为Ai>(Rout+Rmid)/2,mπ/8-π/16≤φi

3 仿真结果及分析

3.1 归一化估计偏差

定义信噪比的归一化估计偏差为[19]

(22)

(a) QPSK

(b) 16APSK

(a) QPSK

(b) 16APSK

图2(a)和(b)分别是估计数据长度为5 000时QPSK调制信号和16APSK调制信号的信噪比估计仿真结果,图3(a)和(b)是对应信噪比估计结果的归一化偏差.

分析图2和图3的结果,得出如下结论:

1) 在信道莱斯衰落因子K=10 dB的条件下,本文提出的估计算法归一化偏差不超过0.2,说明该算法在信道衰落较严重时仍然具有较高的估计精度.

2) 本文提出的信噪比估计算法对低阶和高阶调制具有普适性:对于低阶QPSK调制和高阶16APSK调制,都具有较精确的估计结果,估计偏差不超过0.2.而M2M4算法在高阶16APSK调制下的估计偏差趋近于1,说明该算法已失效,不适用于高阶调制.

3) 本文提出的信噪比估计算法具有较宽的适用范围,在信噪比为5～25 dB范围内都保持较低估计偏差.

3.2 计算复杂度

本文提出的信噪比估计算法需要计算信号幅值Ai和相位φi,可采用CORDIC(coordinate rotation digital computer, CORDIC)算法完成.CORDIC算法的思想是通过迭代方法,不断旋转特定角度,使得累计旋转角度和无限接近某一设定角度.CORDIC算法的每个迭代需要2次移位、1次查找表和3次加法.设每个用于估计的接收帧长度为N,即利用接收到的N个数据进行信噪比估计,则本文算法的时间复杂度为O(N).本文算法的时间复杂度与M2M4算法的时间复杂度相当,远低于文献[12]算法的时间复杂度O(N3)+O(N2M).

4 结语

针对莱斯衰落信道,提出了一种属于判决域的非数据辅助信噪比估计算法.在推导出信噪比与接收信号期望和方差的关系表达式基础上,对接收数据按照相应准则进行数理统计和分析,采用多项式拟合法得到信噪比估计结果.在同样的信道条件和信号采样长度下,本文算法具有估计结果精度高、适用范围宽、适用于低阶和高阶多种调制类型的特点,且计算时间复杂度与M2M4算法相当,是一种高效的信噪比估计方法.

References)

[1]谢显中,刘源源,雷维嘉.高动态环境下基于数据辅助的稳健信噪比估计[J].西南大学学报(自然科学版),2016,38(8):174-181. Xie Xianzhong, Liu Yuanyuan, Lei Weijia. Robust data-aided snr estimation algorithm in high dynamic environment[J].JournalofSouthwestUniversity(NaturalScienceEdition), 2016, 38(8):174-181. (in Chinese)

[2]Li Z X, Yang D W, Wang H, et al. Maximum likelihood SNR estimator for coded MAPSK signals in slow fading channels[C]//Proceedingsof2013InternationalConferenceonWirelessCommunicationsandSignalProcessing. Hangzhou, 2013: 1-6.

[3]Wang A F, Xu H. Comparison of several SNR estimators for QPSK modulations[C]//Proceedingsof2012InternationalConferenceonComputerScienceandServiceSystem. Nanjing, 2012: 77-80. DOI:10.1109/csss.2012.28.

[4]Wang A F, Xu H, Ke J. NDA moment-based SNR estimation for envelope-based QAM[C]//Proceedingsof2012IEEE11thInternationalConferenceonSignalProcessing. Beijing, 2012: 1341-1344. DOI:10.1109/icosp.2012.6491824.

[5]Li W, Zhang Y, Zhang Y, et al. Subspace-based SNR estimator for OFDM system under different channel conditions[C]//Proceedingsof2013IEEEInternationalSymposiumonBroadbandMultimediaSystemsandBroadcasting. London, UK, 2013: 1-5. DOI:10.1109/bmsb.2013.6621687.

[6]许华,王爱粉,杨晓宇.常规数字通信信号信噪比估计综述[J].信号处理,2013,29(6):723-733.DOI:10.3969/j.issn.1003-0530.2013.06.009. Xu Hua, Wang Aifen, Yang Xiaoyu. Survey of the SNR estimation of conventional digital communication signals[J].SignalProcessing, 2013, 29(6): 723-733. DOI:10.3969/j.issn.1003-0530.2013.06.009. (in Chinese)

[7]Pauluzzi D R, Beaulieu N C. A comparison of SNR estimation techniques for the AWGN channel[J].IEEETransactionsonCommunications, 2000, 48(10): 1681-1691. DOI:10.1109/26.871393.

[8]Alagha N S. Cramer-Rao bounds of SNR estimates for BPSK and QPSK modulated signals[J].IEEECommunLetter, 2001, 5(1): 10-12. DOI:10.1109/4234.901810.

[9]陈云峰,付永明,张炜.基于矩方法的通信信号信噪比估计算法研究[J].通信技术,2015,48(1):23-26. DOI:10.3969/j.issn.1002-0802.2015.01.005. Chen Yunfeng, Fu Yongming, Zhang Wei. MoM-based SNR estimation algorithms for communication signals [J].CommunicationTechnology, 2015, 48(1): 23-26. DOI:10.3969/j.issn.1002-0802.2015.01.005. (in Chinese)

[10]Ramesh A, Chockalingam A, Milstein L B. SNR estimation in generalized fading channels and its application to Turbo decoding[C]//2001InternationalConferenceonCommunication. Helsinki, Finland, 2001, 4: 1094-1098. DOI:10.1109/icc.2001.936822.

[11]杨俊,江虹,张秋云.一种改进的非数据辅助SNR估计算法研究[J].计算机科学,2016,43(8):71-73,104. DOI:10.11896/j.issn.1002-137X.2016.8.014. Yang Jun, Jiang Hong, Zhang Qiuyun. Improved non-data-aided SNR estimation algorithm[J].ComputerScience, 2016, 43(8): 71-73, 104. DOI:10.11896/j.issn.1002-137X.2016.8.014. (in Chinese)

[12]韩博,吴杰,许华,等.基于相关向量机的信噪比估计算法[J].通信学报,2013,34(4):201-206.DOI:10.3969/j.issn.1000-436x.2013.04.025. Han Bo, Wu Jie, Xu Hua, et al. New SNR estimation algorithm based on relevance vector machine[J].JournalonCommunications, 2013, 34(4): 201-206. DOI:10.3969/j.issn.1000-436x.2013.04.025. (in Chinese)

[13]李晋,华惊宇,尤肖虎.一种移动通信中的低复杂度盲信噪比估计算法[J].电子与信息学报,2006,28(6):1054-1058. Li Jin, Hua Jingyu, You Xiaohu. A low complexity blind SNR estimator in mobile communication[J].JournalofElectronics&InformationTechnology, 2006, 28(6): 1054-1058. (in Chinese)

[14]张金成,彭华,赵国庆.信噪比估计算法研究[J].信息工程大学学报,2011,12(5):535-543.DOI:10.3969/j.issn.1671-0673.2011.05.005. Zhang Jincheng, Peng Hua, Zhao Guoqing. Research on SNR estimation algorithms[J].JournalofInformationEngineeringUniversity, 2011, 12(5): 535-543. DOI:10.3969/j.issn.1671-0673.2011.05.005. (in Chinese)

[15]Kostov N. Mobile radio channels modeling in Matlab[J].RadioEngineering, 2003, 12(4): 12-16.

[16]刘明骞,李兵兵,王婧舒,等.低信噪比下低复杂度的OFDM信号带宽盲估计方法[J].江苏大学学报(自然科学版),2013,34(1):76-80. DOI:10.3969/j.issn.1671-7775.2013.01.015. Liu Mingqian,Li Bingbing,Wang Jingshu,et al. Bandwidth blind estimation scheme of OFDM signals with low complexity at low SNR[J].JournalofJiangsuUniversity(NaturalScienceEdition), 2013, 34(1): 76-80. DOI:10.3969/j.issn.1671-7775.2013.01.015. (in Chinese)

[17]郑剑文.特定环境下卫星移动通信信道全阴影模型的研究[D].天津:天津大学电子信息工程学院,2007.

[18]周涛,陶成,刘留,等.基于测量的高铁宽带无线信道莱斯K因子研究[J].铁道学报,2013,35(9):72-78. DOI:10.3969/j.issn.1001-8360.2013.09.012. Zhou Tao, Tao Cheng, Liu Liu, et al. Measurement-based research on ricean K-factor of broad-band wireless channel in high-speed railway scenarios[J].JournaloftheChinaRailwaySociety, 2013, 35(9): 72-78. DOI:10.3969/j.issn.1001-8360.2013.09.012. (in Chinese)

[19]华惊宇,黄清,滑翰,等.一种移动环境下的信噪比估计算法及其在多普勒频移估计中的应用[J].通信学报,2005,26(5):132-137.DOI:10.3321/j.issn:1000-436X.2005.05.022. Hua Jingyu, Huang Qing, Hua Han, et al. SNR estimation scheme and its application in Doppler shift estimation in mobile communication systems[J].JournalonCommunications, 2005, 26(5): 132-137. DOI:10.3321/j.issn:1000-436X.2005.05.022. (in Chinese)

An SNR estimation algorithm for Rician fading channel

Chen Ping1,2,3Xiong Weiming1

(1National Space Science Center, Chinese Academy of Sciences, Beijing 100190, China)(2University of Chinese Academy of Sciences, Beijing 100049, China)(3China State Shipbuilding Corporation System Engineering Research Institute, Beijing 100094, China)

Aimed at the problems in Rician fading channel, i.e. general Non-Data-Aided signal-to-noise ratio(SNR) estimation algorithms were very complex and usually suitable for a certain modulation pattern. This paper proposed an SNR estimation algorithm. On the basis of establishing equivalent system model, the relationship expression of SNR, expectation and variance of received signals were deduced. Under the conditions of the Rician fading channel, the deduced expression had no analytic solutions, thus using the polynomial fitting method to obtain approximate solutions of SNR during a certain range. Simulations and comparison experiments show that, the algorithm does not need any training sequence and is universal for both lower and higher order modulations. If the channel Rician factorK=10 dB and the SNR is between 5 and 25 dB, the normalization bias is lower than 0.2, the computational complexity is comparable with M2M4 algorithm, thus satisfying requirements of general engineering application.

signal-to-noise ratio(SNR) estimation; Rician fading channel; polynomial fitting;non-data-aided

10.3969/j.issn.1001-0505.2017.02.002

2016-07-18. 作者简介: 陈萍(1983—)，女，博士生；熊蔚明(联系人)，男，研究员，博士生导师，xwm@nssc.ac.cn.

国家高技术发展计划(863计划)资助项目(2011AA7033045).

陈萍,熊蔚明.一种可用于莱斯衰落信道的信噪比估计算法[J].东南大学学报(自然科学版),2017,47(2):209-214.

10.3969/j.issn.1001-0505.2017.02.002.

TN911.22

A

1001-0505(2017)02-0209-06