近距离隧道轨道列车同时运行引起的环境振动

金学健， 李 双， 李 成， 侯 晋

(苏州大学 城市轨道交通学院，江苏 苏州 215131)

近距离隧道轨道列车同时运行引起的环境振动

金学健， 李 双， 李 成， 侯 晋

(苏州大学 城市轨道交通学院，江苏 苏州 215131)

近距离平行隧道和交叠隧道中轨道列车同时运行引起的环境振动明显高于单列车运行情形，对此类环境振动进行定量计算和预测是一个亟待解决的问题。以苏州轨道交通4号线为背景，建立近距离平行隧道-地基平面有限元模型，研究在不同列车荷载组合、不同隧道间距及不同隧道埋深下的地面振动响应特点和规律，并对数值计算结果进行多项式拟合，得到基于双列车荷载作用下的地面振动预测公式，为工程设计和环境评价提供参考。

环境振动; 轨道交通; 近距离隧道; 有限元模型

随着城市轨道交通的迅猛发展和人们对生活水平要求的提高，轨道列车运行产生的环境振动和噪声问题也逐渐受到重视[1-3]。在轨道交通建设中，涌现了大量近距离平行隧道和交叠隧道，在某一路段，双列车甚至更多列车近距离同时运行，产生的环境振动将明显高于单列车引起的振动，基于单列车荷载的环境振动预测公式已不再适用，如何定量评价是一个重要问题。目前，针对近距离隧道的研究集中在两个方面。一方面是如 SOLIMAN 等[4-5]研究施工时近距离隧道的相互影响；另一方面是如高峰等[6-8]对运营期间近距离隧道结构的动力响应做了分析探究。然而，关于近距离隧道引起的环境振动方面的研究较少。

本文以苏州轨道交通4号线(在建)为背景，研究在不同列车荷载组合、不同隧道间距及不同埋深下的地面振动特性，并对数值模拟结果进行多项式拟合，得到双列车近距离隧道运行时的地面振动预测公式。

1 计算模型

在建中的苏州轨道交通4号线总体呈南北走向，主线全长约42 km，设车站31座，均为地下车站。拟采用B型车，6辆编组，列车长度117.12 m。列车设计最高运行速度为80 km/h。正线、出入段线和试车线采用60 kg/m钢轨，车场线采用50 kg/m钢轨，弹性分开式扣件，正线全部采用整体道床。

轴重、车辆定距和轴距对环境振动有很大影响，车辆定距与列车车速耦合激发低频振动，对环境振动也影响较大。苏州4号线的轨道车辆的类型是确定的，即本文在轴重、车辆定距和轴距给定的条件下进行建模和计算。在本文的计算模型中，输入载荷是轮轨力(我们通过轨道振动测试后推导得到)，不涉及到车辆本身，模型的合理及准确性在文献[9-10]中均得到过验证。实际上，轴重、车辆定距和轴距等参数都是对轮轨力产生直接影响，施加到轨道结构上，进而对环境振动产生影响。

1.1 计算区域

选取苏州4号线团结桥站到宝带东路站间的吴中人民医院所在截面。考虑计算效率与振动影响范围，所取有限元模型区域为120 m×60 m。此截面处隧道间距为12.7 m，隧道埋深为18 m，隧道净空内径为5.5 m，外径为6.2 m，混凝土衬砌厚度为0.35 m。 将有限元模型划分网格后，如图1所示，共有27 141个节点，26 339个单元。d1表示隧道埋深，d2表示隧道间距，d3表示地面拾振点距右侧隧道中心线的距离。其中左侧隧道为左线，右侧隧道为右线，本文为描述方便，所指单列车均为右线列车，下文不一一赘述。

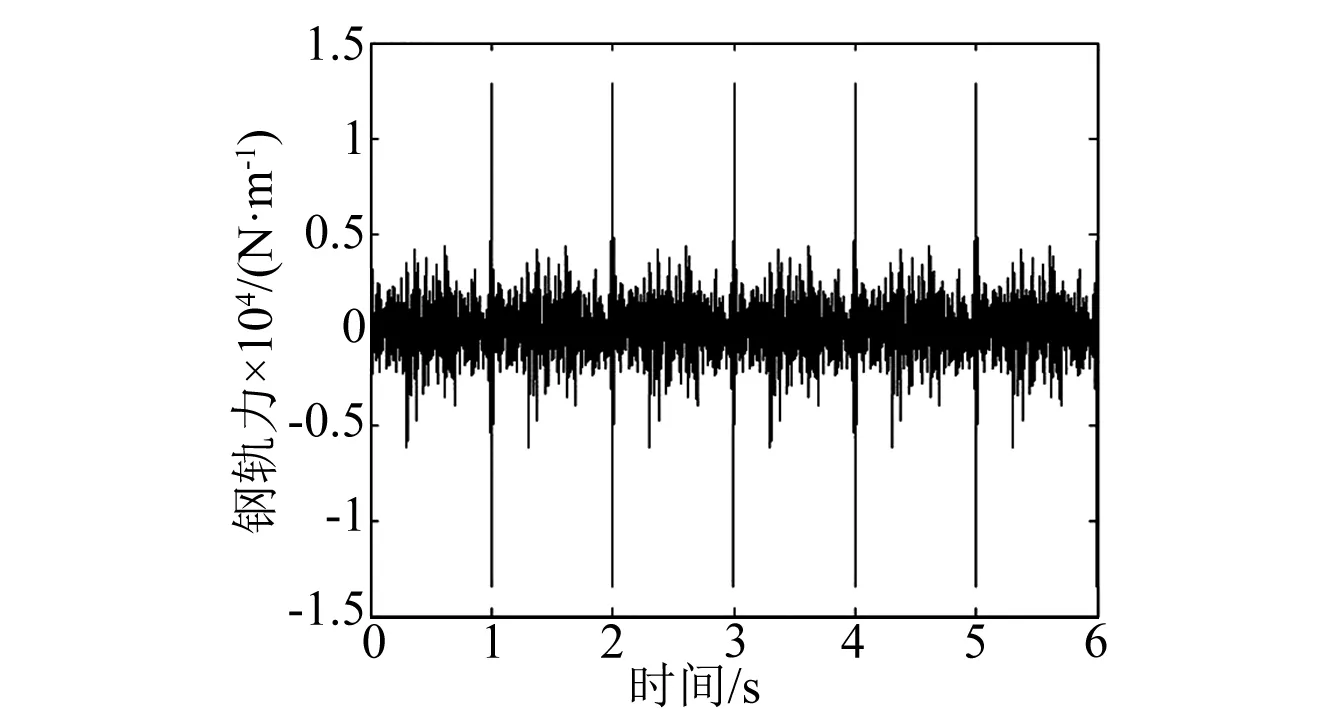
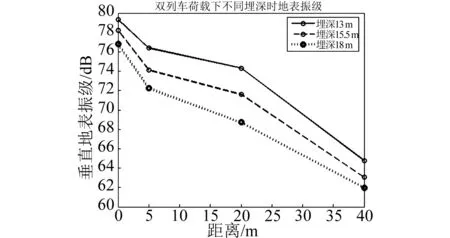
文中有限元模型区域为120 m×60 m，厚度取为0.2 m，根据板壳弯曲理论，按板面内特征尺寸(L)与厚度(h)之比划分，(5～8)

图1 有限元模型Fig.1 Finite element model

1.2 边界条件

本文采用等效一致黏弹性人工边界，即在已经完成的有限元模型的边界上，再沿法向向外，延伸一层相同类型的单元，再将外层边界的各个自由度固定，定义等效单元的材料属性使其作用与一致黏弹性人工边界单元相等价。

1.3 土层与混凝土参数

根据苏州4号线环评报告分析，4号线土质可分为七个工程地质层，本文建模将土层简化为三层。具体土质分布及参数，如表1所示。混凝土参数如表2所示。其中土层采用板单元，混凝土衬砌采用壳单元。

表1 土层分布情况及参数Tab.1 Distribution of soils and parameters

表2 混凝土衬砌参数Tab.2 Concrete lining parameters

1.4 列车荷载

本文所施加的轨道列车荷载，是我们在苏州1号线上通用锤击法测量得到钢轨传递函数，再结合实测的轨道列车通过时的钢轨振动加速度推导得到，如图2所示。

图2 列车荷载时程曲线Fig.2 Time histories of train loads

需要说明的是，我们之前对苏州1号线单列车运行的环境振动计算中运用了上述建模和计算方法，计算结果与实测结果吻合较好，验证了该方法的有效性。

在文中的2D单元模型中，轨道简化为一个点，在该点上施加荷载。本文采取的是瞬态动力学分析(transient)：首先将锤击法测得的6 145个离散数据(一个时间点对应一个力)读取到Ansys中，制成数组，再利用表荷载施加；定义分析类型为瞬态动力学分析，并在solution control中设置时间步长和质量、刚度阻尼等参数；施加轮轨力，进行求解。

2 计算结果及分析

2.1 单、双列车分别作用下的地面振动对比

选取4个拾振点：d3=0 m、 5 m、 20 m、 40 m。

单列车运行时拾振点的加速度如图3所示，左线运行时拾振点加速度曲线与右线列车相似，这里不再列出。双列车运行时各拾振点加速度如图4所示。

(1)时域分析：两种情形下，随着距离增加，地面振动均在衰减。双列车荷载下引起的地面振动加速度幅值显著大于单列车荷载下，但小于单列车荷载下的两倍。

(2)频域分析：两种列车荷载情形下，各拾振点的振动频率集中在40～80 Hz，与相关文献的研究结果一致，50 Hz处频率成分较多；随着振动传播，距隧道中心线距离增加，高频成分衰减较快，振动以低频为主。

2.2 地面Z振级对比分析

在左线、右线及双列车荷载三种工况下，各拾振点对应的垂向振级如图5所示。可以看出：

(1)双列车荷载引起的地面Z振级比右线单列车荷载下高出4 dB以内。

(2)在单、双列车荷载下，地面振动在20 m处均有所回升，存在反弹区，与刘维宁[11]等的研究结论相符。

(3)吴中人民医院距4号线右侧轨道中心线距离为33 m，计算得到左线、右线和双列车荷载作用时，该处Z振级分别为54.5 dB、63.2 dB和64.8 dB。根据中国城市区域环境振动标准，特殊住宅区昼夜均要求低于65 dB,吴中人民医院在三种列车荷载情形下的计算结果均符合振动标准要求。

2.3 隧道埋深对振动影响

考虑最不利情况，当双列车运行时，取隧道间距d2=12.7 m，埋深d1=13 m、15.5 m、18 m时，地面Z振级随距离衰减如图6所示。总结得出，地面振动随隧道埋深增加而降低，埋深每增加2.5 m，地面Z振级降低约3 dB。

图6 不同埋深对应的地表振级随距离衰减曲线Fig.6 Attenuation curve of surface vibration levelwith distance at different depths

2.4 隧道间距对振动影响

考虑最不利情况，当双列车运行时，取隧道埋深d1=18 m，间距d2=7.7 m、8.7 m、12.7 m时，地面Z振级随距离衰减如图7所示。总结得出，双列车作用下，地面振动随隧道间距增加而降低；但隧道间距从7.7 m增加到8.7 m和12.7 m，地面振级降低并不显著，说明了隧道间距对地面振动影响不大。

图7 不同间距对应的地表振级随距离衰减曲线Fig.7 Attenuation curve of surface vibration levelwith distance at different distance

3 双列车荷载下地面振级随距离衰减曲线拟合

以吴中人民医院所在断面计算结果为例，利用多项式拟合出双列车载荷下地面振级随距离的衰减曲线。多项式拟合的优点在于精确度较高，通过拟合得到的公式可作为经验公式，为以后类似工程的设计提供参考。

由于本文取的数据点不多，故采用3次多项式拟合即可。对应的拟合方程表达式为：VLZ=76.61-1.121 7L+0.046 2L2-0.000 7L3，其中VLZ为地面Z振级，单位dB；L表示距离右侧隧道中心线的距离，单位为m。结果如图8所示。

图8 3次多项式拟合曲线Fig.8 Curve of cubic polynomial fitting

4 结 论

(1)两种列车载荷组合下，地面振动频率集中在40～80 Hz，50 Hz频率能量较高。随着振动传播，距隧道中心线距离增加，高频成分衰减较快，振动以低频为主。

(2)双列车运行引起的地面振动显著高于单列车，振动加速度幅值小于单列车荷载下的两倍。双列车引起的地面Z振级比单列车高出4 dB以内。

(3)在单、双列车荷载下，地面振动在20 m处均有所回升，存在反弹区。

(4)双列车运行时，地面振动随隧道埋深增加而降低，埋深每增加2.5 m，地面Z振级降低约3 dB。

(5)双列车作用下，地面振动随隧道间距增加而降低，但降低并不显著，说明隧道间距对地面振动影响不大。

(6)利用多项式对地面振级随距离衰减曲线进行了拟合，得到了拟合公式，可作为双列车运行时地面振动预测的经验公式，为工程设计提供参考。

[ 1 ] 张海滨，蒋伟康，万泉.城市轨道列车噪声辐射特性的试验研究[J].振动与冲击,2010,29(11):83-86. ZHANG Haibin, JIANG Weikang, WAN Quan. Experimental study on the noise radiation characteristics of urban rail train[J]. Journal of Vibration and Shock, 2010, 29(11): 83-86.

[ 2 ] 楼梦麟，李守继.地铁引起建筑物振动评价研究[J].振动与冲击,2007, 26(8):68-71. LOU Menglin, LI Shouji. Evaluation of building vibration caused by subway[J]. Journal of Vibration and Shock, 2007, 26(8): 68-71.

[ 3 ] 侯晋，李双，袁国清,等.苏州轨道交通1号线地面振动测试与分析[J].环境污染与防治,2014, 36(10): 68-72. HOU Jin, LI Shuang, YUAN Guoqing, et al. Suzhou rail transit line 1 ground vibration test and analysis[J]. Environmental Pollution and Control, 2014, 36(10): 68-72.

[ 4 ] SOLIMAN E, DUDDECK H, AHRENS H. Two and three dimensional analysis of closely spaced double-tube tunnel[J]. Tunneling and Underground Space Technology,1993, 8(1): 13-18.

[ 5 ] YAMGUCHI I, YAMAZAKI I, KIRITANI Y. Study of ground-tunnel interactions of four shield tunnels driven in close proximity, in relation to design and construction of parallel shield tunnels[J]. Tunneling and Underground Space Technology, 1998, 13(3): 289-304.

[ 6 ] 高峰，关宝树.列车荷载作用下地铁重叠隧道的响应分析[J].西南交通大学学报, 2003, 38 (1): 38-42. GAO Feng, GUAN Baoshu. Dynamic responses of overlapping tunnels to passing trains[J]. Journal of Southwest Jiaotong University, 2003, 38(1): 38-42.

[ 7 ] 李春峰.地铁列车作用下近距离交叠隧道的动力响应[D].北京：北京交通大学，2006.

[ 8 ] 黎杰，李欢，霍飞.地铁振动荷载作用下交叠隧道衬砌结构响应特性分析[J].公路工程, 2012,37(1): 40-42. LI Jie, LI Huan, HUO Fei. Responses analysis of lining structure of overlapping tunnel to train loads[J]. Journal of Highway Engineering, 2012, 37(1): 40-42.

[ 9 ] 侯晋.苏州城市轨道交通振动计算及测试分析[D].苏州：苏州大学，2014.

[10] 栗润德.地铁列车引起的地面振动及隔振措施研究[D].北京：北京交通大学，2008.

[11] 刘维宁，夏禾.地铁列车振动的环境响应[J].岩石力学与工程学报，1996(增刊1) : 586-593. LIU Weining, XIA He. Environmental response of subway train vibrations[J]. Rock Mechanics and Engineering, 1996(Sup1): 586-593.

Environmental vibration responses of close parallel tunnels under train loads

JIN Xuejian, LI Shuang, LI Cheng, HOU Jin

(School of Urban Rail Transportation, Soochow University, Suzhou 215131, China)

The environmental vibration caused by the simultaneous operation of rail trains in overlapping or close tunnels is higher than that under a single train load. Its quantitative calculation and forecasting is an urgent problem to be solved. A finite element model for analysing the close parallel tunnel-ground structure based on Suzhou Rail Transit Line 4 was established to study its ground vibration responses. The characteristics of ground vibration responses were studied under different train loads combinations, different depth and distance between the two tunnels. The numerical simulation results were processed by using polynomial fitting to get an empirical formula under double train loads. The results can provide references to engineering design and environmental assessment in future.

environmental vibration; rail transportation; close tunnels; finite element model

国家自然科学基金(51375321)；国家级大学生创新创业训练计划项目(201310285050Z)

2015-10-12 修改稿收到日期：2016-02-22

金学健 男，硕士生，1991年生

李双 男，博士，教授，1976年生 E-mail: lishuang@suda.edu.cn

U231；X593

A

10.13465/j.cnki.jvs.2017.06.034