一种基于三轴与单轴随机振动最大应力等效的载荷裁剪方法

王海东， 仇原鹰， 周东亮， 周 磊 ， 李伟明

(1.上海航天精密机械研究所，上海 201600；2. 西安电子科技大学 机电工程学院，西安 710071)

一种基于三轴与单轴随机振动最大应力等效的载荷裁剪方法

王海东1， 仇原鹰2， 周东亮2， 周 磊2， 李伟明1

(1.上海航天精密机械研究所，上海 201600；2. 西安电子科技大学 机电工程学院，西安 710071)

为了避免三轴振动试验对产品造成过试验问题，现以单轴振动试验标准为基准，进行基于三轴振动与单轴依次振动最大响应应力等效的三轴载荷谱裁剪。首先对线性系统在随机振动下激励与响应均方根值的关系进行推导，将单轴振动时的最大等效应力与三轴振动时的最大等效应力的比值n作为三轴振动载荷谱均方根值的裁剪系数，裁剪保持载荷谱扫频范围、拐点频率值以及载荷谱斜线段的斜率N不变，根据梯形谱均方根值计算公式反推出梯形载荷谱直线段谱值，进而得到满足三轴与单轴随机振动最大应力等效的三轴载荷谱。通过对某典型舱段结构进行三轴载荷谱的裁剪，并将载荷谱裁剪后的三轴振动应力响应与载荷谱裁剪前的单轴振动应力响应进行对比，验证了方法的有效性与准确性。

随机振动；应力等效；载荷谱裁减；有限元仿真

随机振动试验是考核导弹、火箭等航天产品结构动强度及环境适应性的重要手段，是暴露结构缺陷和鉴定设备承受使用环境能力的一种有效方法[1]。

工程构件或产品在实际工作中所受的载荷一般是多轴向的，但在传统的随机振动试验中，由于试验技术及试验设备的限制，常以三个正交轴依次进行的单轴振动试验来近似等效多轴振动试验[2]。这种方法简便易行，在工程实践得到了大量应用。在早期的产品研发中发挥了重要作用，并衍生了大量的试验设备、试验方法和标准规范。但随着产品结构的复杂多样化，单轴振动试验的不足越来越明显，主要表现在以下几方面：一维的振动试验无法暴露某些对振动方向敏感，但又不是振动试验方向的故障模式，因此导致了许多按照单轴振动试验标准通过了振动试验的设备在实际使用中出现了故障；对于某些设备，多次的一维的振动试验导致了产品的过试验，使得产品出现了不应有的故障模式；对于大型试验件，由于振动试验与实际环境在振源和振动传递上的不一致，使得同一试验件中不同设备同时存在欠试验和过试验[3]。

由此可见不能简单地将单轴振动试验与多轴振动试验进行等效，大量的实践证明多轴振动环境试验能发现单轴振动试验未能发现的潜在故障，能更真实地模拟实际的振动环境，是更为合理、有效的外场模拟试验方法[4]。但是目前关于三轴振动的试验标准尚且不成熟，建立科学合理的三轴振动试验标准是亟待解决的问题。

近年来，随着对多轴激励振动研究的不断深入，人们意识到，多轴振动激励对结构响应的耦合效应十分复杂，不少学者通过对比某些产品的单轴与多轴振动试验效果来探究二者之间的差异，并获得一些有益的结果[5-6]。美国喷气推进实验室比较了三个一分钟的单轴振动试验(每次一轴)和一分钟的三轴同时振动试验造成的累计疲劳损伤的差别，发现三轴振动产生的累计疲劳是单轴振动的两倍[7]。FRENCH等[8]对典型试件进行了单轴与多轴振动试验研究，结果表明: 多轴向同时振动与单轴向依次振动疲劳试验相比较具有明显的多轴效应，更能导致结构疲劳失效。武芳文等[9]对大跨度斜拉桥结构进行了数值分析，结果表明多维振动下的响应相对于一维激励有明显的差异，总体上使结构的响应更为复杂。王帅等[10]对空间管路结构单、三轴随机振动环境下的疲劳损伤进行研究，发现各节点三轴同时振动的疲劳损伤比单轴依次振动的疲劳损伤均要强。

以上研究均说明在相同的载荷条件下三轴振动试验要比单轴依次交替的振动试验产生更大的响应，即若对三轴振动台按照单轴振动标准加载三个轴向的单轴振动激励谱，会引起产品的过试验和过设计，造成一些不应有的故障模式。但目前关于如何根据单轴振动试验标准建立与之等效的三轴振动试验标准，还鲜有人研究。因此本文根据频域内线性系统随机振动载荷与响应的关系，通过一定比例裁剪三轴输入载荷谱的均方根值，使得三轴振动时的最大等效应力与单轴振动时最大振动方向的最大等效应力相等，进行基于应力等效的三轴振动试验条件研究，并对某典型舱段结构进行单轴与三轴试验，验证该方法的有效性和准确性。该研究为以后的三轴振动试验标准的建立提供参考依据，具有重要的理论及实际意义。

1 线性系统随机激励与响应关系

系统的响应函数或是系统激励和响应在时域和频域内的桥梁。由于本文讨论的是结构在多轴与单轴振动下的最大应力等效问题，故本文从时域与频域角度分析多输入多输出的线性系统在平稳随机激励下，激励与响应之间的传递关系。

本文着重关心最大应力响应点，将问题转化为多输入单输出情况。首先研究两点输入、一点输出的情况，然后推广至多点输入、一点输出的模型。其系统传递模型如图1所示。

其中，x1(t),x2(t)为作用于系统1、2点的输入平稳随机过程；yk(t)为系统k点的输出平稳随机过程；hk1(t)，hk2(t)分别为系统在1→k和2→k之间的传递脉冲响应函数；Hk1(ω)，Hk2(ω)分别为系统在1→k和2→k之间的传递频率响应函数。

根据随机振动相关理论可知，该两输入单出系统的响应自相关函数为

(1)

由自功率谱的定义知，该系统输出应的自功率谱为

(2)

式中，Sx1x2(ω)和Sx2x1(ω)为激励x1(t)和x2(t)的两个互功率谱，反映了两激励R. P.(Random Process)的能量在频域上的相互耦合作用。

对式(2)的结果可以推广，当有n个R. P.x1(t),x2(t),…,xn(t)同时激励时，系统中k点的响应自谱为

(3)

在频域内对式(3)做关于的积分可得到系统响应的均方值，再对其开方得到系统的响应均方根值：

(4)

若这n个激励互不相关，则

(5)

由定义知这些互不相关的激励均方根值为

(6)

若将每个激励的均方根值增加a倍，即

(7)

则每个激励的自相关函数将增加a2倍，此时该系统的响应的均方根值为

(9)

此式表明：对于线性系统，当输入的载荷功率谱均方根值增大a倍时，系统响应的均方根值也增大a倍。这一规律为后文的基于应力等效实现对三轴载荷谱的裁剪奠定理论基础。

2 仿真算例

算例模型选取某典型舱段结构，由三轴振动夹具与舱段组成，如图2所示。

其中夹具的左右盖板通过螺栓连接与舱段两端面紧密贴合。夹具的底座为梯形槽形状，两边与舱段外径相切，用于舱段的夹持和固定，如图3所示。舱段主要尺寸为：长761.9 mm，外径为203.2 mm；夹具的三视图及主要尺寸如图4所示。

图2 舱段与夹具模型总体示意图Fig.2 Layout of the assembled compartment and fixture model

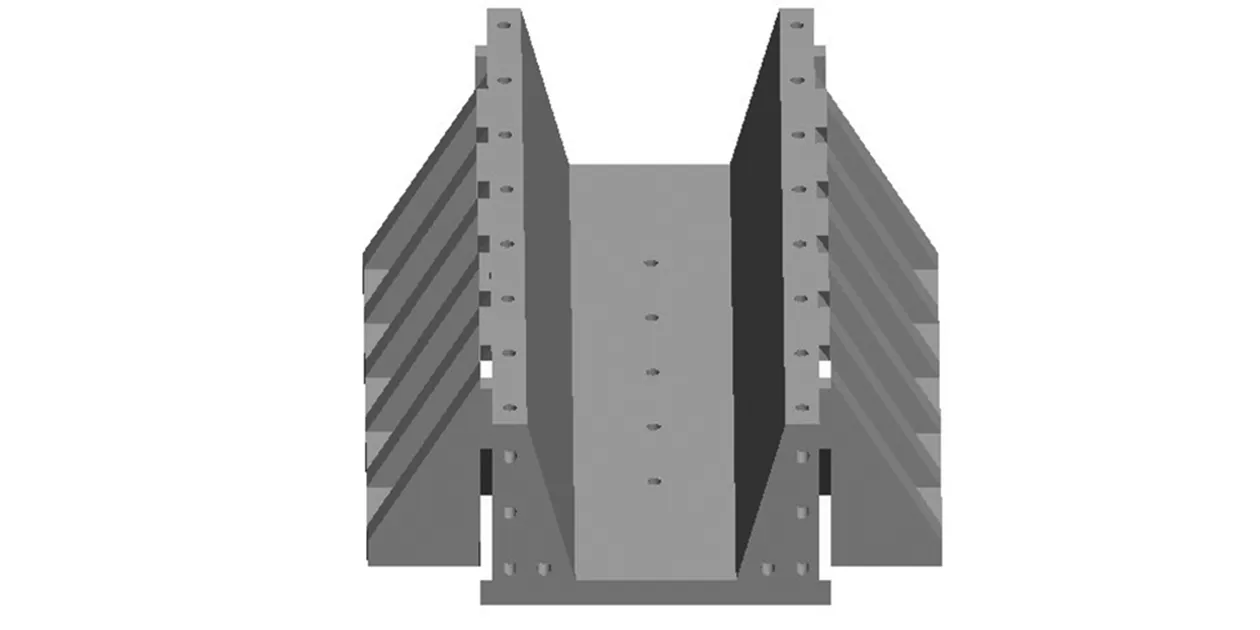
图3 夹具底座梯形槽示意图Fig.3 Trapezoidal groove of the fixture pedestal

图4 夹具模型三视图 Fig.4 Three views of the fixture model

夹具底端为螺栓组排列，通过高强度螺栓与振动台紧固连接，为了更好地模拟实际振动试验情况，将夹具底端面与各螺栓孔内表面均施加全约束，图5中的深色区域为施加的约束，届时载荷激励谱也将通过此处进行加载。

图5 三轴振动试验台夹具约束设置Fig.5 Constraint settings for triazial vibration testing table

根据国军标GJB 150.16—1986提供的单轴随机振动试验谱标准，选择如图6所示的宽带振动谱对结构进行随机振动分析。

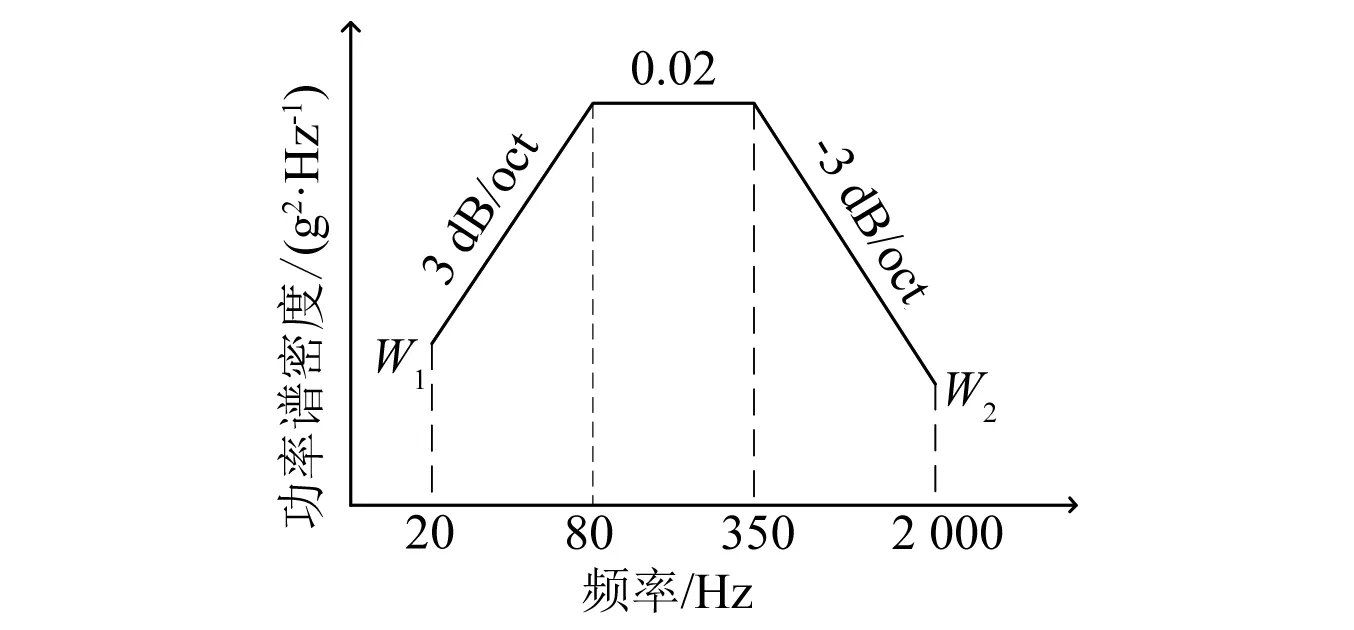
图6 单轴随机振动试验谱Fig.6 Testing spectrum of uniaxial random vibration

图中为双对数坐标，斜率N用分贝/倍频程(dB/oct)表示，即单位倍频程(oct)使功率谱密度值增加或者减少的分贝数(dB)，根据功率谱密度斜率定义[11]，则有：

(10)

式中：fH为上频率(Hz)，fL为下频率(Hz)，在图6中，对应第一段斜直线，fH为80 Hz，fL为20 Hz；对应第二段斜直线，fH为2 000Hz，fL为350 Hz。WH为频率fH处的加速度功率谱密度值(g2/Hz)，WL为频率fL处的加速度功率谱密度值(g2/Hz)。

根据斜率公式(10)计算出基础加速度功率谱S(f)中的W1、W2值，可得：

(80 Hz≤f<350 Hz)

(350 Hz≤f<2 000 Hz)

(11)

对于梯形随机振动加速度功率谱密度函数，其均方根值通常可通过图7所示方法计算。

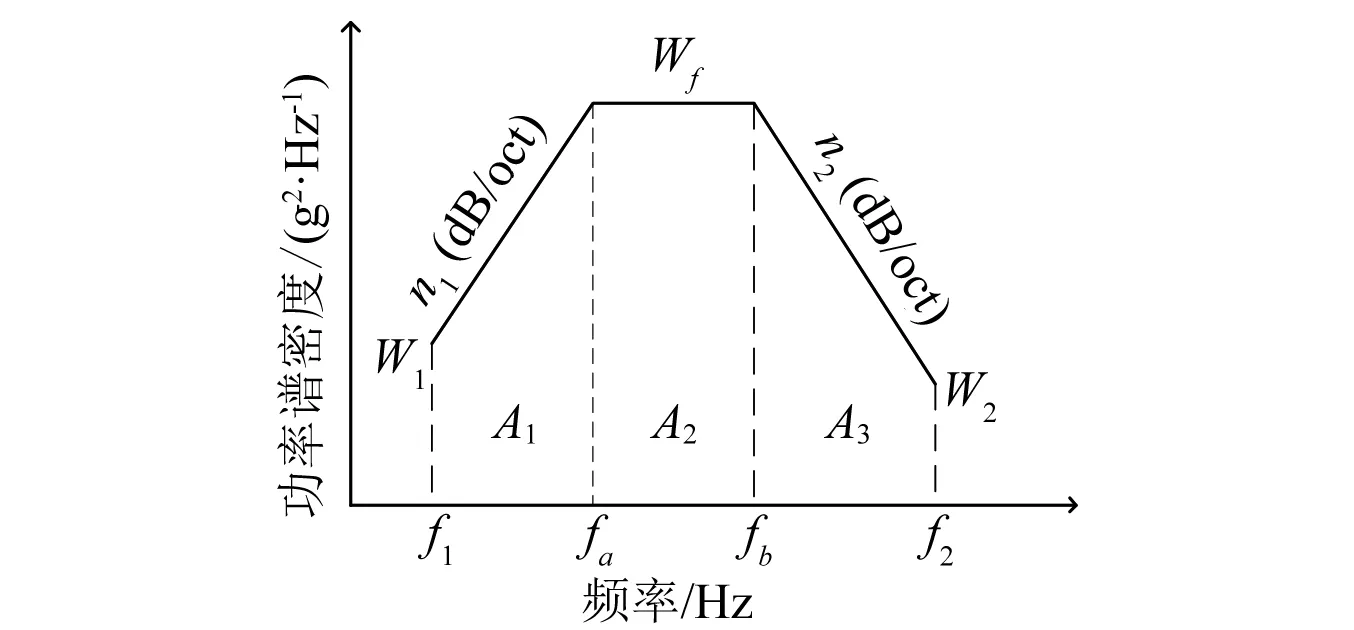
图7 随机振动加速度总均方根值计算图Fig.7 Acceleration rms calculating diagram

对于图7所示的加速度功率谱密度曲线，其均方根值计算[11]过程如下：

上升段：

(12)

式中：m1=n1/3,n1为上升谱谱线的斜率(dB/oct)。

平直段：

A2=W(fa)[fb-fa]

(13)

下降段：

(14)

式中：m2=n2/3,n2为下降谱谱线的斜率(dB/oct)。

当m2=-1时，应用罗比达法则可得

(15)

加速度总均方根值：

(16)

在有限元软件Ansys环境中对典型舱段各零部件进行接触设置，为了等效实际的约束情况，主要设定绑定接触和不分离接触。绑定接触是指两个部件之间面面接触，线线接触，线面接触，不会发生分离或相对滑动，可将它们看作粘合的一体。如典型舱段结构中电器控制盒、电池与外壳之间的接触。不分离接触类似于绑定接触，但其只应用于面面接触。它不允许面面之间发生法向分离，但可以允许接触面发生微小的相对无摩擦滑动，例如典型舱段外壳之间的接触。

网格划分是建立有限元模型的一个重要环节，选择何种类型的单元以及何种方式进行网格划分对计算精度和计算规模将产生直接影响。本文对舱段结构的网格采用人工控制划分与自动网格划分两种方式，以确保网格划分的有效性和合理性。对于舱段结构仿真分析中较为关心的部件，如电气控制盒，将其切分成几个规则的几何体，生成多体部件，以便生成规则的结构网格，对于舱段结构中可扫掠体及规则体应采用扫掠网格划分法和多区域网格划分法，此使得网格划分相对规整，提高网格划分的效率。其余部分零件采用自由网格划分方法，这样划分完成后，共得到284 750个单元，906 848个节点。舱段整体网格划分如图8所示。

图8 舱段结构的网格划分图Fig.8 Meshing of the compartment

对舱段有限元模型，进行如下两种工况研究：在夹具底部固定约束处单独依次加载沿X,Y,Z方向的随机加速度基础谱，模拟传统的振动试验，即三个正交轴依次进行单轴振动试验；同时加载沿X,Y,Z三个方向的随机加速度基础功率谱，模拟三轴振动试验，即三个正交轴同时进行振动试验。提取这两种工况下最大等效应力结果如表1所示。

表1 舱段结构单轴与三轴振动的应力比较(1σ值)Tab.1 Maximum equivalent stress contrast of the compartment (1σ value)

可见对于该舱段三轴同时加载激励要比单轴依次加载产生的等效应力大，且X向单独加载激励时的等效应力为单轴依次加载中最大的，可以说X轴向是最大振动方向。由式(9)知，要使三轴振动时的最大等效应力值(20.031 MPa)缩减到单轴振动时最大振动方向的最大等效应力值(14.567 MPa)，必须对输入的梯形谱均方根值做裁剪。

本文裁剪的原则是保持输入载荷谱扫频范围以及各拐点的频率值不变，同时保持对数功率谱密度曲线中斜线段的斜率N也不变，改变输入载荷谱的直线段的谱值，起点和终点的W1、W2的值也随之改变。由于线性系统输入与输出之间满足线性关系，现要使三轴同时激励时响应的均方根值缩减14.567/20.031=0.727倍，那么三轴振动时的输入梯形谱均方根也要缩减0.727倍。即裁剪后的梯形谱均方根值为grms=4.282×0.723=3.114(g)。

通过式(12)～式(16)可反算出裁剪后的梯形谱直线段值为0.010 6。裁剪前后的梯形谱对比如图9所示。

其中虚线表示裁剪前的载荷谱，实线表示裁剪后载荷谱。

图9 裁剪前后梯形谱对比Fig.9 Trapezoidal spectrum contrast after clipping

在Workbench中将裁剪后的梯形谱同时加载到X，Y，Z三个方向，进行三轴振动试验，并将分析所得的等效应力结果与载荷谱裁剪前的X轴单向加载时的等效应力进行对比分析如下表2所示。

表2 单轴振动的等效应力与裁剪后三轴振动的等效应力对比Tab.2 Maximum equivalent stress contrast after clipping

由表2可见，载荷谱裁剪后的三轴随机振动的最大等效应力值与单轴依次振动时最大振动方向的最大等效应力值基本一致，误差仅为0.006 8%。因此采用该原理进行载荷谱裁剪可有效实现应力等效。

3 结 论

本文根据线性系统在频域内随机振动载荷与响应关系，提出了一种基于三轴振动与单轴依次振动时最大应力等效的三轴载荷谱裁剪方法，裁剪原则是保持载荷谱扫频范围、拐点频率值以及载荷谱斜线段的斜率N不变，改变载荷谱直线段谱值，起点和终点的、的值也随之改变。针对典型舱段结构的随机振动仿真试验，应用该方法对三轴振动谱进行裁剪，把裁剪后的三轴振动应力响应与裁剪前的单轴依次振动时最大振动方向的应力响应进行对比，得到其相对误差仅为0.006 8%，具有很高的精度，验证了该方法的准确性和有效性。

[ 1 ] 陈立伟，卫国. 多维随机振动试验条件制定方法研究[J]. 强度与环境, 2010,37 (6): 1-6. CHEN Liwei, WEI Guo. Methodology of design conditions for multi-axis random vibration test [J]. Structure & Environment Engineering, 2010, 37(6): 1-6.

[ 2 ] 贺光宗，陈怀海，贺旭东. 一种多轴向随机激励下结构疲劳寿命分析方法[J]. 振动与冲击， 2015，34 (7): 59-63. HE Guangzong, CHEN Huaihai, HE Xudong.Vibration fatigue life prediction method for structures under multi-axial random excitations [J]. Journal of Vibration and Shock, 2015, 34(7): 59-63.

[ 3 ] 陈颖，朱长春，李春芝. 典型结构在单、多轴随机振动下的动力学特性对比研究[J]. 振动工程学报， 2009,22(4): 386-390. CHEN Ying, ZHU Changchun, LI Chunzhi. Contrast research for dynamic charactistic of a typical structure under uniaxial and triaxial random vibration [J]. Journal of Vibration Engineering, 2009, 22(4): 386-390.

[ 4 ] 农绍宁，田光明，赵怀耘. 多维激励下结构随机振动响应分析[J].装备环境工程,2013,10(2):124-128. NONG Shaoning, TIAN Guangming, ZHAO Huaigen. Random vibration response analysis of structures under multi-dimensional excitation [J]. Equipment Environmental Engineering, 2013, 10(2): 124-128.

[ 5 ] GREGORY D， BITSIE F， SMALLWOOD D O. Comparison of the response of a simple structure to single axis and multiple axis random vibration inputs[C]∥ Proceedings of the 79th Shock and Vibration Symposium. Orlando: 2008.

[ 6 ] PAULUS M E. Fatigue damage accumulation due to complex random vibration environments: application to single-axis and multi-axis vibration[D]. College Park: University of Maryland, 2011.

[ 7 ] SCHARTON T.Force limited vibration testing at JPL[C]∥Aerospace Testing Seminar, 14th. Manhattan Beach, CA, 1993: 241-251.

[ 8 ] FRENCH R M， HANDY R， COOPER H L． Comparison of simultaneous and sequential single axis durability testing [J]．Experimental Techniques， 2006，30( 5) : 32-35.

[ 9 ] 武芳文，薛成凤，赵雷. 多维地震激励作用下大跨度斜拉桥的随机响应[J]. 武汉理工大学学报，2010，32(9)：344-347.

WU Fangwen, XUE Chenfeng, ZHAO Lei. Stochastic response of long-span cable-stayed bridge under multi-component seismic excitation [J]. Journal of Wuhan University of Technology, 2010, 32(9): 344-347.

[10] 王帅,李佰灵,贾亮.空间管路结构单多轴随机振动环境下的疲劳损伤研究[J]. 强度与环境,2012,12(6):36-41. WANG Shuai, LI Bailing, JIA Liang. The fatigue damage research of space pipeline structures under uniaxial/multiaxial random vibration [J]. Structure & Environment Engineering, 2012, 12(6): 36-41.

[11] 常研.随机振动试验的几个工程问题[J].电子机械工程,2002,18(2): 46-69. CHANG Yan. Some engineering problems about random vibration test [J]. Electro-mechanical Engineering, 2002, 18(2): 46-69.

Load clipping method based on the maximum stress equivalence between triaxial and uniaxial random vibration

WANG Haidong1，QIU Yuanying2，ZHOU Dongliang2, ZHOU Lei2, LI Weiming1

(1. Shanghai Spaceflight Precision Machinery Research Institute, Shanghai 201600,China；2. School of Electromechanical Engineering, Xidian University,Xi’an 710071,China)

To avoid over test in triaxial vibration tests on products, the triaxial load spectrum clipping was introduced based on the equivalence of the maximum response stress in triaxial vibration that in successive uniaxial vibrations using the uniaxial vibration testing standard as a benchmark. The relationship between the excitation and response rms values of a linear system under random vibration was deduced and the rationof maximum equivalent stress in uniaxial vibration to that in triaxial vibration was adopted as a clipping coefficient for the rms value of triaxial vibration load spectrum. While doing the clipping, the load spectrum sweep range, the corner frequency value and the slopeNof oblique line segment in the load spectrum were kept unchanged. Then, the spectrum values at the straight section of load spectrum were figured out according to the rms value calculation formula for trapezoid spectrum so as to get a triaxial load spectrum that meets the stress equivalence between triaxial and uniaxial random vibrations. Through the clipping on the triaxial load spectrum of a certain typical missile compartment and contrasting the triaxial vibration responses after load spectrum clipping with the uniaxial vibration responses before clipping, the validity and accuracy of the method were verified.

random vibration; stress equivalence; load spectrum clipping; finite element analysis(FEA)

航天八院核心攀登工程项目(ZY2013-004)

2015-10-23 修改稿收到日期： 2016-02-24

王海东 男，本科，高级工程师，1975年生

仇原鹰 男，博士，博士生导师，1958年生

O32

A

10.13465/j.cnki.jvs.2017.06.012