基于变分模态分解的机械故障诊断方法研究
2017-04-11李志农朱明
李志农, 朱明
(南昌航空大学 无损检测技术教育部重点实验室, 江西 南昌 330063)
基于变分模态分解的机械故障诊断方法研究
李志农, 朱明
(南昌航空大学 无损检测技术教育部重点实验室, 江西 南昌 330063)
变分模态分解(VMD)是一种新的自适应信号分解方法,该方法的核心思想是假设每个模态的绝大部分都是紧紧围绕在某一中心频率周围的,然后将模态带宽的求解问题转化为约束优化问题,求解出每个模态。将VMD引入到机械故障诊断中,提出一种基于VMD的机械故障诊断方法,并与集合经验模态分解(EEMD)方法进行对比分析。仿真结果表明:VMD方法明显优于EEMD方法,能有效地分解出信号的固有模态;与EEMD方法相比较,该方法模态混叠现象弱,计算效率高,理论充分。将VMD方法成功地应用到转子不同碰摩严重程度的故障数据分析实验中,实验结果进一步验证了该方法的有效性,能够揭示出碰摩故障数据的频率结构,区分碰摩故障的严重程度。
机械学; 变分模态分解; 故障诊断; 集合经验模态分解; 转子碰摩
0 引言
经验模态分解[1](EMD)能根据信号在时间尺度上的局部特征结构,自适应地提取反映信号本质特征的固有模态分量,其分解过程是过完备的且几乎是正交的,时频聚焦性良好,特别适用于非线性非平稳信号的分析处理。目前,基于EMD的机械故障诊断方法取得了很大的进展[2-10],然而,EMD方法的主要问题是其缺乏数学理论,建模困难,另外还存在端点效应、模态混叠、计算量大等问题[11-15]。针对EMD方法存在模态混叠的缺点,Wu等[16]将噪声辅助信号分析的方法引入到EMD方法中,以减少模态混叠的现象,即集合经验模态分解(EEMD)方法。该方法通过对信号多次加入均值为零的高斯白噪声,反复计算EMD分解求均值,得到最终固有模态,使信号在时间尺度上具有连续的特性,有效地抑制了模态混叠现象。然而,不论是EMD方法,还是EEMD方法,它们在抗噪性、计算效率、理论完备性方面仍存在欠缺。针对EMD方法存在的不足,Dragomiretskiy等[17]结合维纳滤波、Hilbert变换和频率混合,于2014年创造性地提出了一种新的完全非递归自适应信号处理方法,即变分模态分解(VMD)方法。该方法的核心思想是假设每个模态的绝大部分都是紧紧围绕在某一中心频率周围的,然后将模态带宽的求解问题转化为约束优化问题,求解出每个模态。对提取出的每个模态进行Hilbert变换,可得到有意义的瞬时频率和瞬时幅值,进而可以得Hilbert谱。基于VMD的独特优势,本文将VMD引入到机械故障诊断中,提出了一种基于VMD的机械故障诊断方法,并与EEMD进行了对比分析,仿真结果验证了本文提出的方法的有效性。最后,将提出的方法成功地应用到转子不同碰摩严重程度的故障数据分析中,实验结果进一步验证了该方法的有效性。
1 变分模态分解
VMD的实质是将一个实信号f(t)分解成为K个具有特定稀疏性的相互独立子信号uk(变分模态)。在原始信号的频率域,每个模态uk以中心频率ωk进行分解,且频带宽度为紧凑型。因此,在VMD中,最主要的是如何将每个模态的带宽估计出来。这里采用以下方法来估计:
1)通过计算每个模态uk的Hilbert变换获得各自的单边频谱。
2)对于每个模态,通过将其与指数信号相乘,调整相应的估计的中心频率,从而筛选出 “基带”。
3)对解调后的信号进行H1高斯平滑估计求带宽,即梯度L2范数的平方。故受约束的变分问题可为
(1)

为了重建该问题,在此使用具有良好有限收敛特性的二次罚和具有严格执行约束能力的拉格朗日乘数λ, 因此,引入增强型拉格朗日算子L:
(2)
(2)式的优化过程如下:
1)最小化uk:
(3)
2)最小化ωk:
(4)
VMD的具体实现过程如下:
2) 重复n←n+1;
3)k从1到K:
① 对所有的ω≥0更新k:
(5)
② 更新ωk:
(6)
对于所有ω≥0,双上升步长:
(7)
直到满足收敛条件:
(8)
式中:ε是事先设定的收敛误差。
通过VMD后,得到一个信号的变分模态uk后,就可以对每个变分模态函数进行Hilbert变换,从而得到有意义的瞬时频率和瞬时幅值,进而得到Hilbert谱。
2 仿真研究
为了验证VMD的有效性,在此,分别构造了3个含不同异常事件(噪声、间断信号和脉冲干扰)的,可以引起EMD模态混叠的信号。EEMD在模态混叠抑制方面有一定的效果[16],为了体现VMD的有效性,本文也给出了EEMD的结果。仿真信号x1(t)由调幅调频信号x11(t)、调幅信号x12(t)和随机噪声x13(t)组成,其时域波形如图1(a)所示。这里,采样频率1 000 Hz,采样点数为1 000.
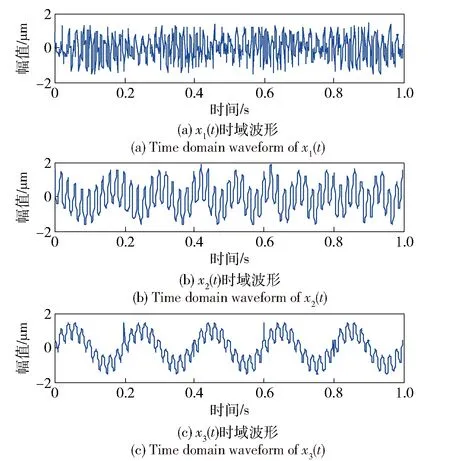
图1 仿真信号时域波形Fig.1 Time domain waveforms of simulation signals
(9)
仿真信号x2(t)由线性调频信号x21(t)、正弦信号x22(t)和间断信号x23(t)组成,其时域波形如图1(b)所示。
(10)
(11)
仿真信号x3(t)由正弦信号x31(t)、正弦信号x32(t)和脉冲干扰信号x33(t)组成,其时域波形如图1(c)所示。
(12)
(13)
图2为含随机噪声的仿真信号x1(t)的3层VMD,可知,随机噪声x13(t)、调频信号x11(t)和调幅信号x12(t)被有效地分解出来了。图3为x1(t)的4层EEMD,噪声得到了一定的分解,但是其他两个模态分量则出现了不同程度的模态混叠现象。因此,VMD与EEMD相比,其抗噪性更强,且其能有效地解决噪声引起的模态混叠。
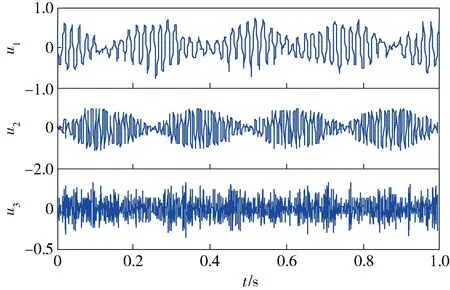
图2 信号x1(t)的VMDFig.2 VMD of x1(t)
图4为含间断信号的仿真信号x2(t)的3层VMD,可知,间断信号x23(t)、线性调频信号x21(t)和正弦信号x22(t)也被有效地分解出来了。图5为x2(t)的4层EEMD,可知,固有模态c1为间断信号x23(t),但是c1夹杂着一部分正弦信号;固有模态c2为正弦信号x22(t),但是在间断信号x23(t)出现的时刻都出现了部分信号缺失;固有模态c3在间断信号x23(t)出现的时刻表现出了一定的间断信号特征,但是与间断信号的频率不同;残余分量r为线性调频信号x21(t),但是出现了一定的失真。因此,VMD与EEMD相比,其能有效地解决间断信号引起的模态混叠。

图4 信号x2(t)的VMDFig.4 VMD of x2(t)
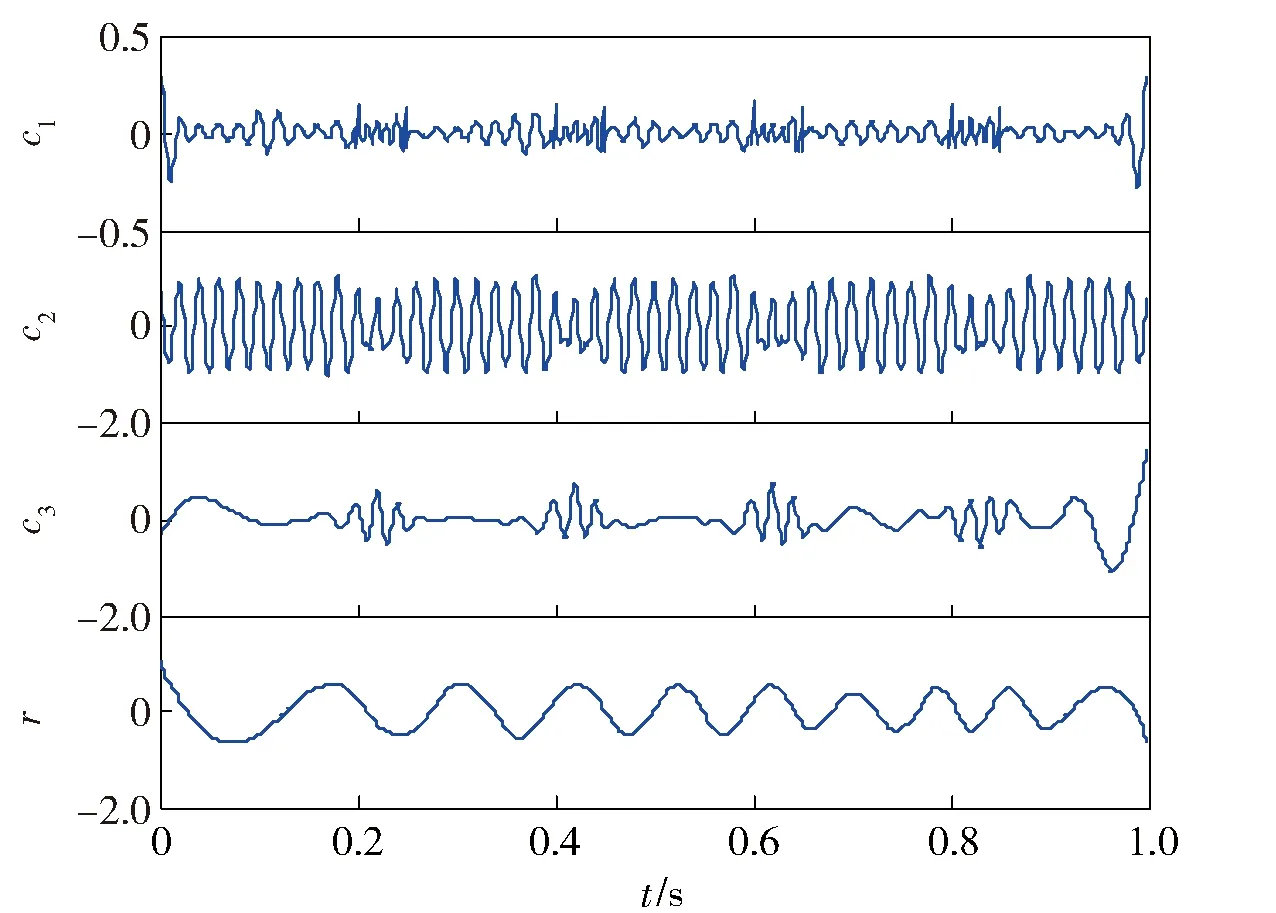
图5 号x2(t)的EEMDFig.5 EEMD of x2(t)
图6为含脉冲信号的仿真信号x3(t)的3层VMD,正弦信号x31(t)、正弦信号x32(t)和脉冲干扰信号x33(t)得到了很好的分解。图7为x3(t)的4层EEMD,由图7可知,脉冲信号x33(t)并不能明显的在固有模态c1上完全的表现出来;固有模态c2为正弦信号x32(t),但出现了一定的失真,固有模态c2表现出了脉冲信号间隔出现的特征,但不能体现脉冲信号自身的特征;残余分量r为正弦信号x31(t)。因此,VMD与EEMD相比,其能有效地解决脉冲信号引起的模态混叠。

图6 信号x3(t)的VMDFig.6 VMD of x3(t)

图7 信号x3(t)的EEMDFig.7 EEMD of x3(t)
通过以上分析可知,VMD能有效地解决模态混叠问题,且其抗噪性明显优于EEMD,又由于VMD算法是在频率域进行的,为完全非递归算法,因此其运算效率比EEMD高。并且,VMD有着完备的数学理论基础,这是EMD所不具备的。由此可知,在处理非平稳非线性信号方面,VMD有着更广阔的应用前景。
3 实验研究
为进一步验证VMD的有效性,将VMD应用到双盘转子的碰摩数据分析中,碰摩转子实验台如图8所示[18-20]。实验台采用直流并励电动机驱动方案,电机轴经联轴器直接驱动转子,结构简单、调速范围宽,且平稳可靠,用非接触式电涡流传感器测量垂直与水平方向的振动。
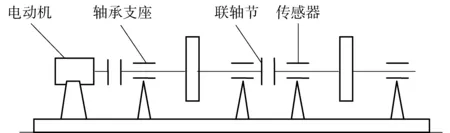
图8 实验台简图Fig.8 Schematic diagram of testbed
为了能更好地模拟出实际碰摩的过程,专门设计了一个有可能产生全周碰摩的定子,如图9所示。其特点:安装、拆卸方便;定子与转子之间可以调整间隙,满足不同的实验条件,结构简单、紧凑。为了减少转子圆盘的磨损,定子采用比较软的铝合金制作,同时设计了3个定子内套,定子内套的内径分别比转子外径大0.4 mm、0.6 mm和0.8 mm. 用4个螺栓调整定子与转子的间隙,支撑架采用钢结构以增加定子的刚度。这样,不但可以调节定子与转子的同心度(使定子和转子之间的间隙比较均匀),还能通过更换定子内套以调节定子和转子之间的间隙大小,从而调节碰摩发生的时间和碰摩的严重程度。

图9 定子结构示意图Fig.9 Schematic diagram of stator
实验是在转速为3 000 r/min工况下进行的,采样频率为1.6 kHz,采样点数为1 024. 利用传感器获得两种不同碰摩程度下的振动信号及其频谱图,分别如图10和图11所示。

图10 碰摩故障信号Fig.10 Rub-impact fault signals
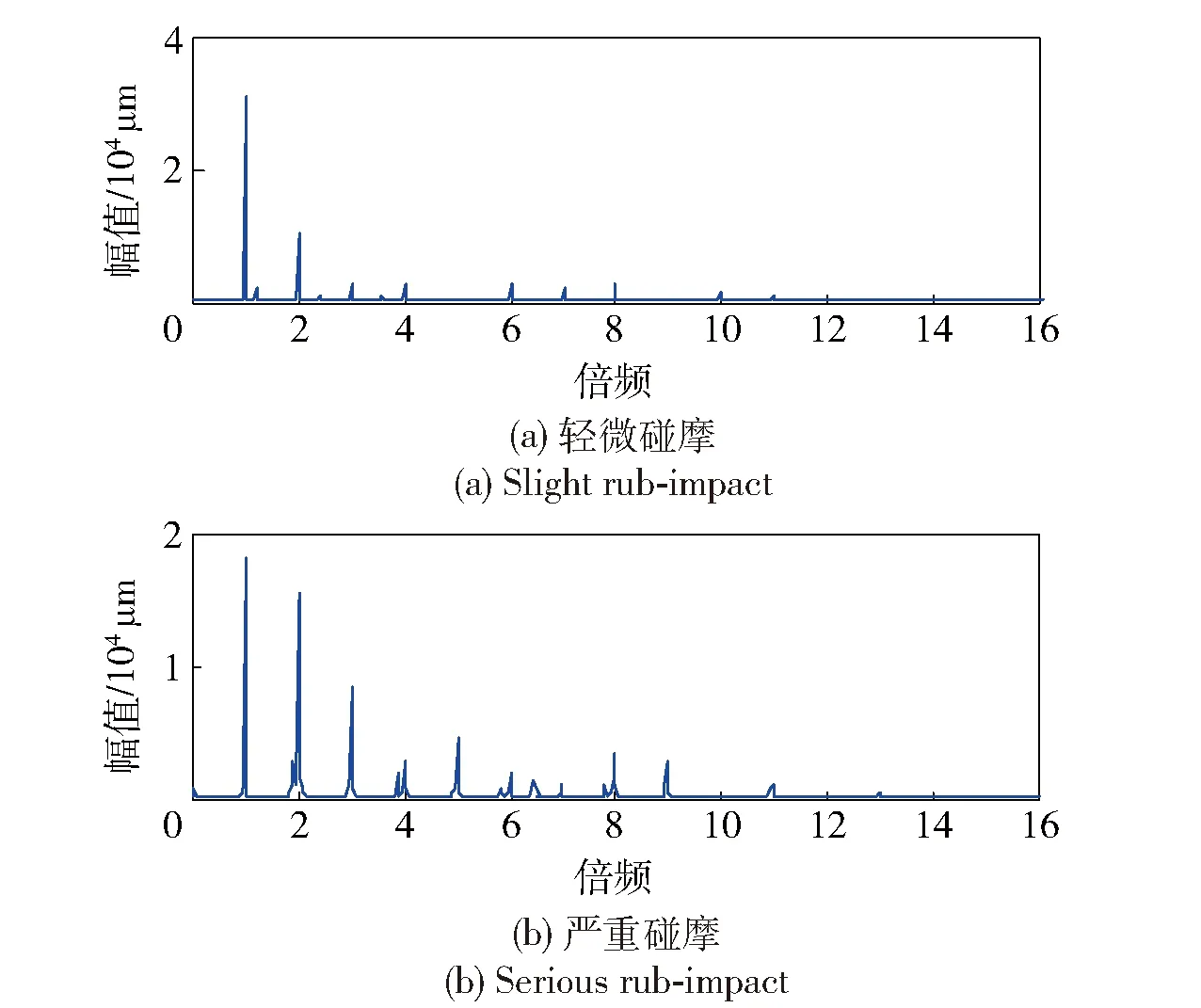
图11 碰摩故障信号的频谱图Fig.11 Spectrum of rub-impact fault signals
由图11(a)可知:轻微碰摩发生时,信号的频谱图主要显示的是1倍频和2倍频,而其他倍频成分在频谱图上则显得很小。由图11(b)可知:严重碰摩发生时,信号的频率成分显得很丰富,然而在频谱中,并不能反映出信号频率随时间变化的特点。

图12 碰摩故障信号的VMDFig.12 VMD of rub-impact fault signals
图12(a)为图10(a)轻微碰摩时信号的5层VMD,可以看出,高阶频率分量u3、u4、u5表现为周期性的冲击信号,但相对于低阶频率分量明显非常微弱。轻微碰摩的VMD-Hilbert谱如图13(a)所示,在1倍频和2倍频分量反映明显,幅值基本上比较稳定,且持续存在,而在高阶部分主要集中在6倍频和8倍频之间,且十分微弱,都是周期性地被激发。图12(b)为图10(b)严重碰摩时信号的10层VMD,可以看出,严重碰摩时,频率成分十分丰富,且高阶频率分量的幅值也很大,u5、u8、u9、u10高阶频率分量都表现出了一定的冲击特性。从图13(b)可知,严重碰摩的Hilbert谱在1倍频、2倍频持续存在,且幅值基本保持不变,而在更高阶频率成分,如3倍频、5倍频、6倍频、8倍频反映的也比轻微碰摩时更加明显,并且较有规律地间断地出现。
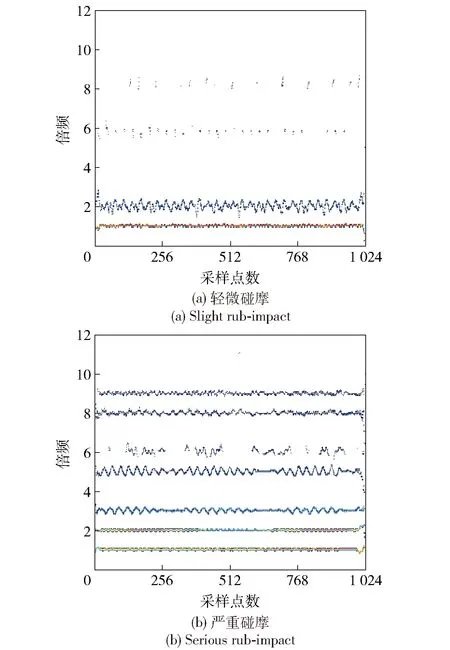
图13 碰摩故障信号的VMD-Hilbert谱Fig.13 VMD-Hilbert spectrum of rub-impact fault signals
通过以上分析可知,VMD能够按照频率特征有效的从低频到高频自适应地分解碰摩故障信号。Hilbert谱能够很好的反映出碰摩故障的严重程度,揭示出碰摩故障的频率特征结构。当故障为轻微碰摩时,低阶频率分量持续存在,且幅值基本保持不变,高阶频率分量则很微弱,随着碰摩严重程度的增加,低阶频率分量依然持续存在,更高阶的频率成分的幅值则会周期性变化,并且幅值明显增大。
4 结论
VMD方法是一种刚刚兴起的完全非递归自适应信号分解方法,该方法的核心思想是假设每个模态的绝大部分都是紧紧围绕在中心频率ωk周围的。将模态带宽的求解问题转化为约束优化问题,求解出每个模态,对提取出的模态进行Hilbert变换,得到有意义的瞬时频率和瞬时幅值,从而可以得到Hilbert谱。本文详细地介绍了该方法,并将该方法引用到机械故障诊断中,提出了基于VMD的机械故障诊断方法,并进行了仿真和实验研究。仿真结果表明,该方法在模态混叠抑制、抗噪性、计算效率、理论完备性等方面都优于传统的EEMD分解。最后,本文将VMD成功应用到转子碰摩故障诊断中,实验结果表明该方法能够有效地揭示出碰摩故障数据的频率结构,区分碰摩故障的严重程度。相信这种新的VMD将会广泛地应用到各种非平稳信号处理领域,且在机械故障诊断领域有广阔的应用前景。
References)
[1] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London A, 1998, 454: 903-995.
[3] Singh S, Kumar N. Combined rotor fault diagnosis in rotating machinery using empirical mode decomposition[J]. Journal of Mechanical Science and Technology, 2014, 28(12): 4869-4876.
[4] Guo W, Peter W T. A novel signal compression method based on optimal ensemble empirical mode decomposition for bearing vibration signals[J]. Journal of sound and vibration, 2013, 332(2): 423-441.
[5] Lu L, Yan J, de Silva C W. Dominant feature selection for the fault diagnosis of rotary machines using modified genetic algorithm and empirical mode decomposition[J]. Journal of Sound and Vibration, 2015, 344(5): 464-483.
[6] Jiang F, Zhu Z, Li W, et al. Fault diagnosis of rotating machinery based on noise reduction using empirical mode decomposition and singular value decomposition[J]. Journal of Vibroengineering, 2015, 17(1): 164-174.
[7] Yu D, Yang Y, Cheng J. Application of time-frequency entropy method based on Hilbert-Huang transform to gear fault diagnosis[J]. Measurement, 2007, 40(9): 823-830.
[8] Peng Z K, Peter W T, Chu F L. A comparison study of improved Hilbert-Huang transform and wavelet transform: application to fault diagnosis for rolling bearing[J]. Mechanical Systems and Signal Processing, 2005, 19(5): 974-988.
[9] 王玉静, 姜义成, 康守强, 等. 基于优化集合 EMD 的滚动轴承故障位置及性能退化程度诊断方法[J]. 仪器仪表学报, 2013, 34(8): 1834-1840. WANG Yu-jing, JIANG Yi-cheng, KANG Shou-qiang, et al. Diagnosis method of fault location and performance degradation degree of rolling bearing based on optimal ensemble EMD[J]. Chinese Journal of Scientific Instrument, 2013, 34(8):1834-1840. (in Chinese)
[10] 姜万录, 刘云杰, 朱勇. 小波脊线解调与两次 EMD 分解相结合的故障识别方法及应用研究[J]. 仪器仪表学报, 2013, 34(5): 1131-1138. JIANG Wan-lu, LIU Yun-jie, ZHU Yong. Research on wavelet ridge demodulation and twice EMD-based fault identification method and its application[J]. Chinese Journal of Scientific Instrument, 2013, 34(5): 1131-1138. (in Chinese)
[11] Li Y, Xu M, Wei Y, et al. An improvement EMD method based on the optimized rational Hermite interpolation approach and its application to gear fault diagnosis[J]. Measurement, 2015, 63(3): 330-345.
[12] Yu Y L, Li W, Sheng D R, et al. A novel sensor fault diagnosis method based on modified ensemble empirical mode decomposition and probabilistic neural network[J]. Measurement, 2015, 68(5): 328-336.
[13] 李志农, 朱明, 褚福磊,等. 基于经验小波变换的机械故障诊断方法研究[J]. 仪器仪表学报, 2014, 35(11): 2423-2432. LI Zhi-nong, ZHU Ming, CHU Fu-lei, et al. Mechanical fault diagnosis method based on empirical wavelet transform[J]. Chinese Journal of Scientific Instrument, 2014, 35(11): 2423-2432. (in Chinese)
[14] 程军圣,于德介,杨宇. 基于支持矢量回归机的Hilbert-Huang变换端点效应问题的处理方法[J]. 机械工程学报, 2006, 42(4): 23-31. CHENG Jun-sheng, YU De-jie, YANG Yu. Process method for end effects of Hilbert-Huang transform based on support vector regression machines[J]. Journal of Mechanical Engineering, 2006, 42(4): 23-31. (in Chinese)
[15] Xu G L, Wang X T, Xu X G, et al. Improved EMD for the analysis of FM signals[J]. Mechanical Systems and Signal Processing, 2012, 33(11): 181-196.
[16] Wu Z, Huang N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41.
[17] Dragomiretskiy K, Zosso D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544.
[18] 褚福磊, 彭志科, 冯志鹏, 等. 机械故障诊断中的现代信号处理方法[M]. 北京:科学出版社, 2009. CHU Fu-lei, PENG Zhi-ke, FENG Zhi-peng, et al. Modern signal processing method for mechanical fault diagnosis[M]. Beijing: Science Press, 2009. (in Chinese)
[19] 朱明, 李志农, 何旭平, 等. 广义S变换在转子碰摩故障诊断中的应用研究[J]. 华侨大学学报, 2014, 35(2): 127-131. ZHU Ming, LI Zhi-nong, HE Xu-ping, et al. Application of generalized S transform in rotor rub-impact fault diagnosis[J]. Journal of Huaqiao University, 2014, 35(2): 127-131. (in Chinese)
[20] Peng Z K, Chu F L, Tse P W. Singularity analysis of the vibration signals by means of wavelet modulus maximal method[J]. Mechanical Systems and Signal Processing, 2007, 21(2):780-794.
Research on Mechanical Fault Diagnosis Method Based on Variational Mode Decomposition
LI Zhi-nong, ZHU Ming
(Key Laboratory of Nondestructive Testing of the Ministry of Education, Nanchang Hangkong University, Nanchang 330063, Jiangxi, China)
Variational mode decomposition (VMD) is a new adaptive signal decomposition method. The idea of this method is that most of each mode is assumed to be tightly around a center frequency, the solving problem of mode bandwidth is converted into an optimization problem with the constrain conditions, and finally each modal is solved. VMD is introduced into the mechanical fault diagnosis, and a fault diagnosis method based on VMD is proposed. The proposed method is compared with the ensemble empirical mode decomposition (EEMD). The simulated result shows VMD method is superior to EEMD method, the intrinsic mode of signal can be effectively decomposed by the VMD method. Compared with the EEMD method, the proposed method has some distinct advantages, such as weak mode mixing phenomenon, high calculation efficiency and sufficient theory. The proposed method has been successfully applied to the rub-impact fault diagnosis of rotor system. The experimental results show that the proposed method is effective, and can effectively reveal the frequency structure in rubbing fault and discern the severity of rub-impact fault.
mechanics; variational mode decomposition; fault diagnosis; ensemble empirical mode decomposition; rotor rubbing
2016-06-23
国家自然科学基金项目(51675258、51265039、51075372、50775208);机械传动国家重点实验室开放基金项目(SKLMT-KFKT-201514);广东省数字信号与图像处理技术重点实验室基金项目(2014GDDSIPL-01); 国家重点研发计划项目(2016YFF0203000)
李志农(1966—),男,教授。E-mail: lizhinong@tsinghua.org.cn
TH165+.3
A
1000-1093(2017)03-0593-07
10.3969/j.issn.1000-1093.2017.03.024
