弹性高超声速飞行器预设性能精细姿态控制
2017-04-11赵贺伟杨秀霞沈如松胡云安
赵贺伟, 杨秀霞, 沈如松, 胡云安
(海军航空工程学院 控制工程系, 山东 烟台 264001)
弹性高超声速飞行器预设性能精细姿态控制
赵贺伟, 杨秀霞, 沈如松, 胡云安
(海军航空工程学院 控制工程系, 山东 烟台 264001)
将反演控制技术、预设性能控制和神经网络相结合,研究设计巡航飞行的高超声速飞行器精细姿态控制器。研究中考虑了高超声速飞行器弹性形变对飞行攻角的影响,引入诱发攻角的概念来刻画气动弹性对飞行器的影响;在考虑弹性的情况下,利用预设性能的设计来满足精细姿态控制的指标要求,同时可以兼顾系统的瞬态性能;利用全局调节动态神经网络在线逼近诱发攻角方程中的未知项,利用Lyapunov稳定性理论得到神经网络权值、中心点和影响范围的自适应调节律,引入鲁棒项来处理神经网络逼近误差的影响,最终设计出考虑气动弹性情况下的高超声速飞行器预设性能精细姿态控制器。通过Lyapunov稳定性理论证明了系统的稳定性以及闭环系统所有信号均有界,仿真分析验证了所设计的控制器能够使系统跟踪误差满足预设性能的要求,以此实现姿态精细控制。
兵器科学与技术; 高超声速飞行器; 气动弹性; 预设性能; 精细姿态控制; 诱发攻角
0 引言
高超声速飞行器是指飞行速度马赫数大于5,在临近空间实现高超声速飞行的飞行器。高超声速飞行器广泛使用轻质柔性材料,导致飞行器结构的固有频率较低,机体弹性形变对飞行器的飞行稳定性以及动力学特性等产生影响[1]。目前,大量的学者投入到高超声速飞行器的控制研究中,使用的高超声速飞行器模型包括美国航空航天局公布的锥形体模型[2]、基于计算流体力学的数值模型[3]、一体化解析式的气动推进/弹性模型[4]以及Bolender等提出的一体化解析式动力学模型[5]。Bolender等提出的一体化解析式动力学模型是被广大学者充分认可和使用的,其很好地刻画了弹性高超声速飞行器纵向运动动力学行为,但是其用来描述弹性模态的方程引入了6个弹性变量来描述弹性问题,这大大增加了系统的维数,给控制器的设计带来了巨大的困难和挑战,因此一种简单的、面向控制的描述弹性模态的非线性模型是急切需要的。
在巡航段的高超声速飞行器需要进行精细姿态控制,因为吸气式高超声速飞行器的超燃冲压发动机对飞行攻角的要求十分苛刻,对飞行攻角控制精度的降低会严重影响超燃冲压发动机的工作品质,从而影响高超声速飞行器的飞行稳定性。然而高超声速飞行器并非纯刚体,在飞行过程中会产生弹性形变,这些结构信息通过传感器反馈到舵系统,会严重影响飞行控制系统的控制精度。因此,高超声速飞行器的气动弹性问题研究不仅仅要研究其稳定性,而且要研究考虑气动弹性的情况下,进一步提高高超声速飞行器的姿态控制精度,实现精细姿态控制,这是高超声速飞行器气动弹性问题的研究与传统飞行器气动弹性问题研究的不同之处。然而,考虑气动弹性问题的高超声速飞行器控制系统设计的难度已经很大了,要想实现考虑气动弹性的高超声速飞行器精细姿态控制是十分困难的,需要找到一种面向控制的弹性模型情况下,利用一种可行的控制方法和手段来实现。文献[6]考虑了高超声速飞行器的弹性问题,进行了多胞鲁棒变增益控制器的设计,其主要是将弹性模态作为系统的干扰项来处理,且没有研究在考虑弹性问题情况下飞行器的精细姿态控制问题;还有的文献采用了结构动力学的线性变参数控制方法[7]、鲁棒自适应控制方法[8]、神经网络自适应方法[9-10]等。虽然这些文献都对弹性问题开展了一定的研究工作,但是它们仅仅考虑了如何使弹性模态稳定,而在考虑弹性问题的情况下如何实现精细姿态控制问题并没有考虑。高超声速飞行器弹性问题的研究区别于普通飞行器弹性问题研究的重要特征就是考虑弹性问题的情况下如何实现想要的控制效果。文献[11]对高超声速飞行器的弹性问题进行了研究,给出了诱发攻角的概念,为弹性问题的研究提供了新思路,尤其是对精细姿态控制问题提供了解决途径。预设性能控制是希腊学者Bechlioulis等[12]提出的一种控制方法,这种控制方法可以兼顾系统的瞬态和稳态性能。所谓预设性能就是指在保证跟踪误差收敛到一个预先设定任意小区域的同时,保证收敛速度及超调量满足预先设定的条件。文献[13]利用预设性能控制设计了弹性高超声速飞行器控制系统,但是该文将系统的弹性模态作为不确定性来处理,不能够反映弹性模态对飞行器攻角的影响,更难以实现精细姿态控制。文献[14]利用预设性能控制设计了高超声速飞行器的纵向内环控制器,其并未考虑弹性问题,将飞行器视为纯刚体,并且没有考虑精细姿态控制问题,这使得设计的方法具有很大的局限性。目前,在考虑弹性问题的情况下,利用预设性能控制技术,实现高超声速飞行器的精细姿态控制的相关文献还很罕见。
本文针对一种吸气式高超声速飞行器,任务背景为飞行器的巡航阶段,考虑高超声速飞行器的气动弹性问题,引入诱发攻角的概念,利用诱发攻角的非线性模型来刻画气动弹性对飞行器的影响,采用Backstepping技术和预设性能控制相结合的方法设计控制器,利用预设性能来实现飞行器的精细姿态控制。
1 系统描述和预备知识
1.1 系统描述
本文研究的某型高超声速飞行器纵向动力学模型的刚体部分[15]如下形式:
(1)

(2)
(3)
(4)
式中:v为飞行器的飞行速度;T为发动机推力;α为攻角;D为阻力;g为重力常数;γ为航迹倾斜角;m为飞行器质量;H为飞行高度;L为升力;q为俯仰角速度;Iq为转动惯量;M为俯仰力矩。
系统的输入量为升降舵偏角δe和燃料当量比Φ. 系统中的力和力矩表达式为
(5)
(6)
(7)
(8)
(9)
(10)
(11)
CM,δe(δe)=ceδe,
(12)
(13)
(14)
(15)
(16)

本文研究的某型高超声速飞行器纵向动力学模型的气动弹性部分采用诱发攻角的非线性模型来描述,文献[11]已经验证了引入诱发攻角的概念来刻画高超声速飞行器的弹性形变特性的可行性。利用文献[11]的分析方法,分析过程不再赘述。将飞行器机体前部和后部视为两个一端固定的悬臂梁,本文只关心弹性形变对攻角的影响,因此只考虑机体前端的悬臂梁。利用激波膨胀波理论来分析和求取高超声速飞行器表面的气流特性,采用一阶活塞理论来分析高超声速飞行器的机体表面受到的气动力。通过分析可知,机体前端弹性形变的微分在机体前端的值即为机体前端表面微元的法向振动速度。当机体前端偏转角足够小时,弹性形变引起的偏转角与定点处的挠度之间存在线性关系,这个偏转角与攻角叠加,共同决定了机体各表面的气流特性。因此定义此物理量为诱发攻角,用符号αr表示,则可用诱发攻角的公式来表征气动力和弹性形变,具体形式为
(17)
式中:
(18)
(19)
Lf为机体的前体长度,为常值,
w1=-N1ρ1b1cosτ1+N2ρ2b2cosτ2+N3ρ3b3,
(20)
w2=N1p1+N2p2+N3p3,
(21)
p1、p2、p3为飞行器表面3个气流分区上的压力,ρ1、ρ2、ρ3为3个气流分区上的来流空气密度,b1、b2、b3为3个气流分区上的来流速度,τ1、τ2分别为飞行器中轴线与上斜面和下斜面的夹角,
(22)
(23)
(24)
E为弹性模态量,I为弯曲惯性矩,Lghf为机体一长度量,为常值。上述分析和推导过程参考文献[11],各符号量的具体物理意义参考文献[16]。
分析系统模型可知,飞行速度v和高度H相比较于攻角α和俯仰角速度q为慢变量,因此可将高超声速飞行器纵向运动模型分为短周期模型和长周期模型,为使研究更具针对性,本文仅对短周期模型进行研究,即
(25)
(26)
(27)
对上述模型进行整理,取αf=α+αr,其中αf为发动机进气口当地攻角,因此可知
(28)
式中:
(29)
设定控制目标如下:
1) 根据给定的期望指令信号αd,设计backstepping预设性能控制器,保证输出信号αf能够跟踪期望指令信号αd的同时,闭环系统中的所有误差信号有界;
2) 输出误差e(t)=αf-αd满足预先设定的稳态和瞬态性能。为达到精细姿态控制的指标要求,满足高超声速飞行器在巡航段保证超燃冲压发动机工作需要的最优姿态条件,即在巡航段平衡状态下发动机当地攻角控制在±1°,姿态角速度≤2°/s,当地攻角跟踪期望指令信号的跟踪误差保持在±0.15°范围内[17]。
作如下假设:
假设1期望指令信号及其各阶导数均为已知,并连续有界。
假设 2初始误差|e(0)|=|αf(0)-αd(0)|有界,且上界为已知常数。
1.2 性能函数
定义1连续函数λ(t):R+→R+为性能函数,其满足下列条件:
1)λ(t)为正且严格递减;
为实现控制目标2,选取如下不等式:
-κλ(t)
(30)
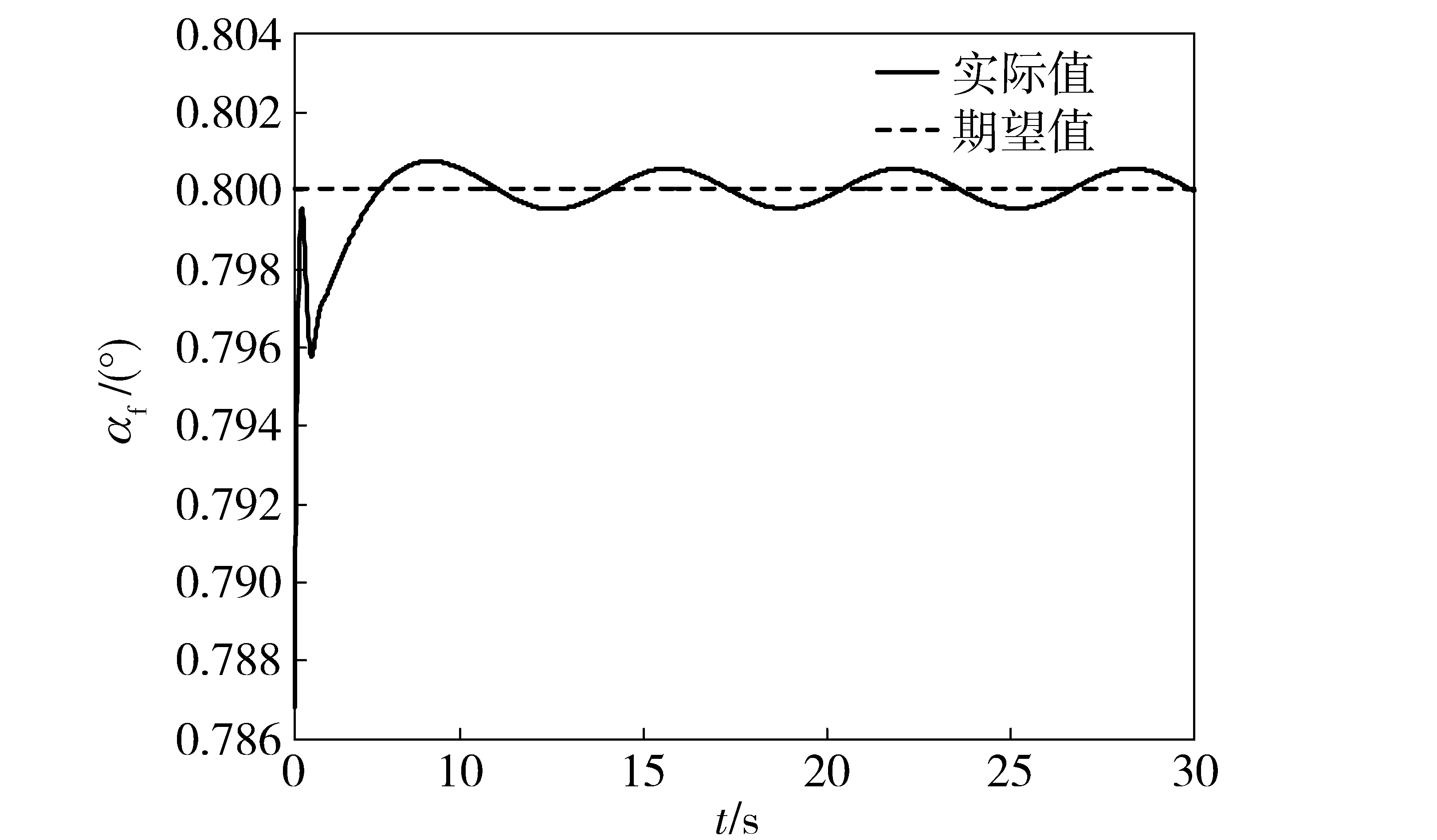
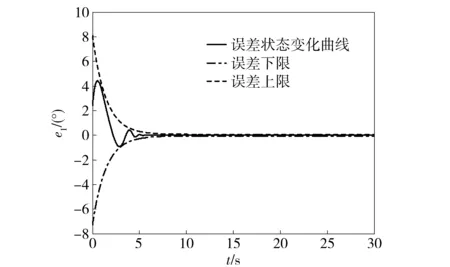
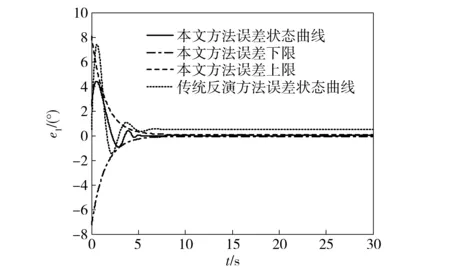
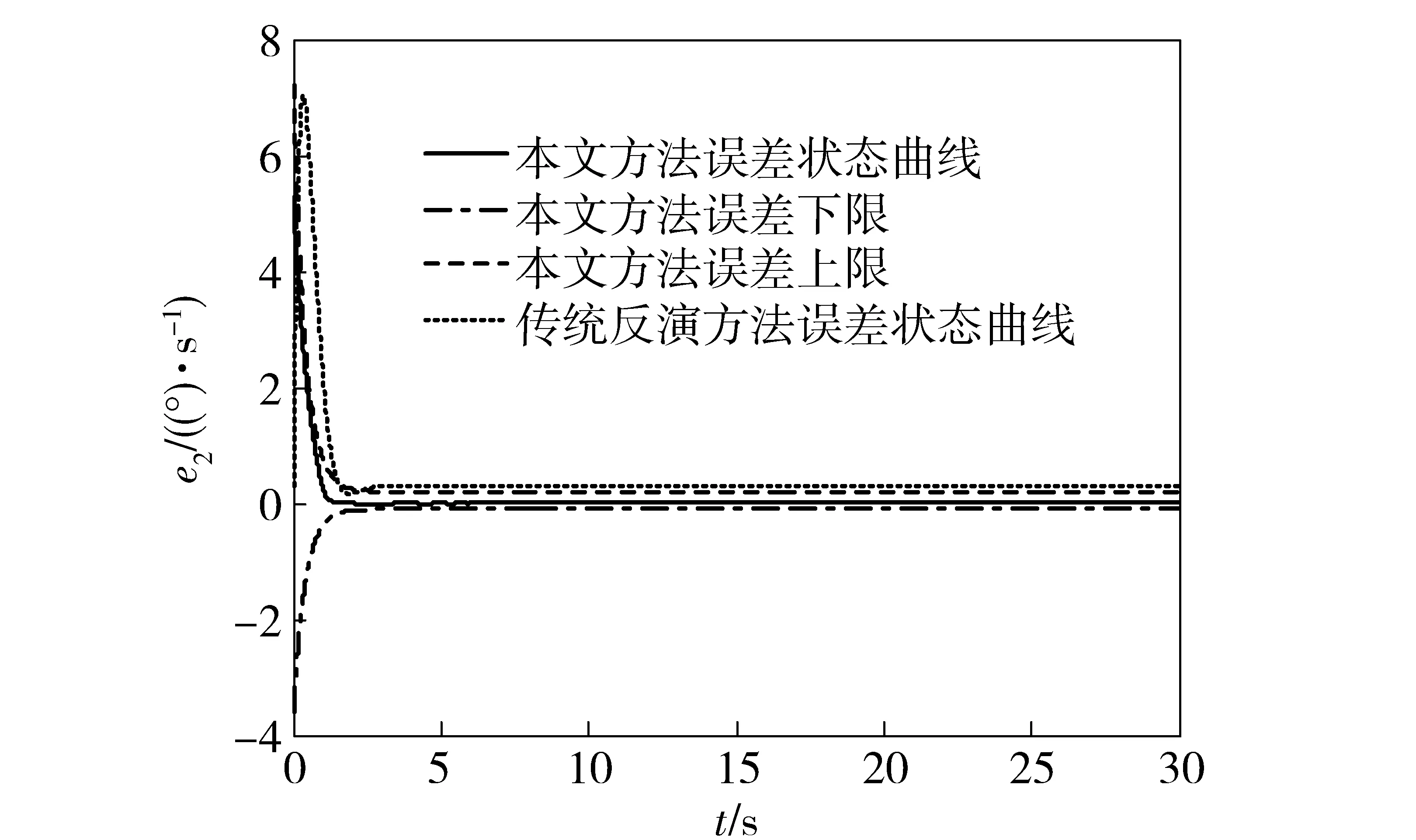
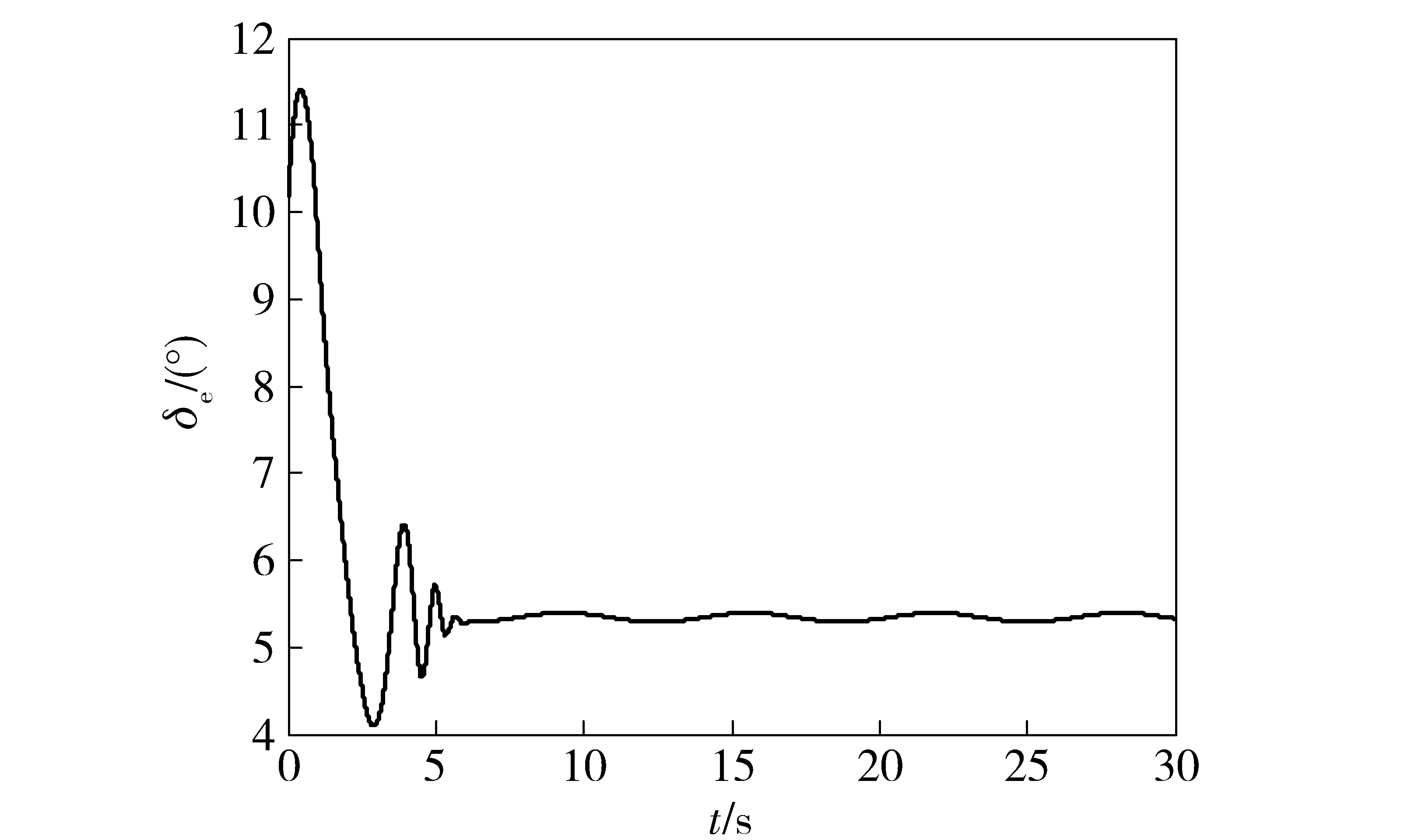
-λ(t) (31) 式中:t∈[0,∞);κ∈[0,1]. 将性能函数选取为 λ(t)=(λ0-λ∞)e-ζt+λ∞, (32) 式中:λ0、λ∞、ζ>0为预先设定的常数,λ∞为预先设定的稳态误差的上限。跟踪误差e(t)收敛速度的下界等于λ(t)的衰减速度,并保证e(t)的最大超调量不大于κλ0. 综上所述,通过选择合适的性能函数λ(t)以及常数κ,则可以实现对跟踪误差的稳态性能和瞬态性能进行限制,可用图1来说明。 图1 性能函数与跟踪误差的关系Fig.1 Relationship between performance function and tracking error 1.3 误差转化 在控制系统设计过程中,不等式约束(30)式、(31)式处理的难度很大,所以需要将其转化为等式约束,具体转化过程如下: 定义跟踪误差为 e(t)=λ(t)G(ε), (33) 式中:ε为转化误差,G(ε)为误差转化函数,且满足如下性质: 1)误差转化函数G(ε)是光滑的,并且严格递增; 2)G(ε)满足如下不等式: 3)G(ε)满足如下等式: 根据前述定义,λ(t)>0,当e(0)>0时,则-κλ(t)<λ(t)G(ε)<λ(t),根据(33)式可知-κλ(t) 根据误差转化函数的性质,进一步将误差转化函数进行逆变换,得 式中:P=G-1. 如果ε(t)∈l∞,t∈[0,∞),可得(30)式、 (31)式成立。同时,根据性能函数严格递减的性质可以判断跟踪误差终将被限制在如下区域: Ω={e∈R:|e(t)|≤λ∞}。 为避免ε(0)→∞,当e(0)=0时,κ不能设定为0. 根据假设2,选择λ(0)>|e(0)|。 1.4 全局调节动态神经网络 函数Δf:ΩRr,Ω为Rn的一个紧子集,对于任意χ>0,总存在一个最优高斯基函数矢量φ*:RnRl和一个最优权重矩阵W*∈Rl×r,使得Δf=W*Tφ*+χ,φ*为最优中心点,l为隐层节点个数为最优的影响范围,X∈Rn为径向基函数(RBF)神经网络的输入向量,χ为RBF神经网络的重构误差[19]。全局调节动态神经网络是利用自适应调节律将神经网络的最优权重矩阵、最优中心点和最优影响范围进行在线调节,与一般的神经网络相比,其逼近能力、适应性更强。 假设3忽略升降舵偏角δe对升力L产生的影响。 根据假设3对系统(26)式、(28)式、(29)式进行整理可得 (34) (35) 式中:Fα=Fr+f1, Fr=η1αr+η2, (36) (37) (38) (39) 上述模型将气动弹性对攻角的影响考虑在内。 步骤1定义跟踪误差为e1=αf-αd,αd为指令信号。同时定义误差转化函数为e1=λ1G1(ε1),e1和ε1的导数分别为 (40) (41) 定义第2个跟踪误差e2=q-qd,其中qd为q的期望指令信号,将(41)式进行整理可得 (42) (43) 式中:残留项du的上界为 (44) 其他各项符号(下文同)及证明过程参考文献[20]。 定义Lyapunov函数为 (45) 对(45)式求时间的导数,可得 (46) 将(42)式代入到(46)式,整理可得 (47) 设计虚拟控制量为 (48) 式中:k1为设计参数;r为需要设计的鲁棒项。将(48)式代入到(47)式,可得 (49) 将(49)式进一步整理可得 (50) 设计神经网络各参量的自适应调节律为 (51) (52) (53) 式中:δW、δμ、δσ>0为设计参数;′ξi、′σi和i分别表示′ξ、′σ和的第i行向量。 将自适应调节律(51)式~ (53)式代入到(50)式,可得 (54) 步骤2定义误差转化函数e2=λ2G2(ε2),可以得到e2、ε2的导数为 (55) (56) 定义Lyapunov函数为 (57) 将(57)式对时间求导,可得 (58) 将(54)式代入(58)式,可得 (59) 将(56)式代入(59)式,可得 (60) 设计系统实际控制律为 (61) 式中:k2为设计参数。 将控制律(61)式代入(60)式,可得 (62) 由(62)式可知 (63) 根据引理1可知,当|ε2|≥0.881 4τ2时, (64) 将(64)式代入到(63)式,可得 (65) 考虑到不等式 (65)式可变换为 (66) 再根据du的上界可知, (67) 设计鲁棒项为 r=-ε1a1(‖T′ξ‖2+‖T′σ‖2+ (68) 式中:z为设计的正常数。再根据如下不等式 (69) 可将(67)式进一步整理为 (70) 将(70)式进一步整理可得 (71) (72) 式中:C为有界常数。 由(71)式可得 (73) 式中: (74) λmax(·)为求矩阵最大特征根。根据(73)式可知 (74) 根据(74)式及选取的Lyapunov函数可知 (75) (76) (77) (78) (79) 式中:λmin(·)为求矩阵的最小特征根。通过 (75)式~(79)式可知,闭环系统所有信号均有界且收敛到系统原点的一个领域内。 针对弹性高超声速飞行器短周期系统(25)式~(27)式,在考虑弹性形变引起诱发攻角的的情况下,在满足假设1~3条件下,采用虚拟控制量(48)式和实际控制量(61)式,全局调节动态神经网络各参量的自适应调节律为(51)式~(53)式,同时在鲁棒项(68)式的作用下,合理地选取预设性能函数和设计参数,可以保证发动机进气口当地攻角αf能够跟踪期望指令信号αd,俯仰角速度q能够跟踪期望指令信号qd,并且满足精细姿态控制的指标要求,同时可以兼顾系统的瞬态性能,并保证闭环系统所有信号均有界。 采用本文的控制方法,控制系统的结构图为图2所示。 图2 控制系统结构图Fig.2 Block diagram of control system 为了验证设计控制系统的有效性和正确性,进行仿真分析,气动力及力矩系数采用文献[15]中的数据,具体在表1中给出。控制参数设计为: 图3为攻角跟踪曲线,根据图3可以看出,实际的飞行攻角可以很好地跟踪期望指令信号。图4为 表1 气动力和力矩系数Tab.1 Values of force and moment coefficients 图3 攻角跟踪仿真结果1Fig.3 Simulated result 1 of angle of attack 攻角稳态时的放大图,通过图4可以得知飞行攻角跟踪期望轨迹的跟踪误差可以稳定在一定的范围之内。图5为俯仰角速度跟踪曲线,可以看出俯仰角速度能够很好地跟踪期望指令信号,而且动态性能比较理想。图6为误差e1的变化曲线及预设性能曲线,可以得到误差e1始终保持在预设性能的可行域内,其具有较短的调节时间和较小的超调量,稳态误差同样满足预设性能要求。图7为本文提出的方法误差e1变化曲线和传统反演方法误差e1的变化曲线比较图,通过图7中的结果可以看出,本文采用的方法误差e1的调节时间和超调量均优于传统的反演方法,且本文采用的预设性能方法可以保证稳态误差限定在一定的范围内,且满足精细姿态控制的指标要求。图8为误差e2的变化曲线和预设性能曲线图,通过图8中结果可以得知误差e2的曲线始终在预设性能的可行域内,其瞬态性能和稳态性能均满足预设性能要求,同时满足精细姿态控制的指标要求。图9为本文采用的方法与传统反演方法比较图,从图9中可以看出本文采用的方法中误差e2的瞬态性能和稳态性能均优于传统的反演方法。图10为俯仰舵偏角变化曲线,其光滑连续并在可行范围内。通过上述仿真结果可以说明本文设计的控制器优于传统的反演控制方法,充分体现了本文设计方法的优越性。同时,对性能函数和误差转化函数进行了合理的设计,使系统全状态误差满足预先设定的稳态性能要求,从而实现了飞行器的精细姿态控制。 图4 攻角跟踪仿真结果2Fig.4 Simulated result 2 of angle of attack 图5 俯仰角速度仿真结果Fig.5 Simulated result of pitch angular rate 图6 e1及预设性能曲线Fig.6 Curves of e1 and prescribed performance 图7 e1变化曲线Fig.7 Curves of e1 图8 e2及预设性能曲线Fig.8 Curves of e2 and prescribed performance 图9 e2变化曲线Fig.9 Curves of e2 图10 俯仰舵偏角仿真结果Fig.10 Simulated result of elevator deflection 本文针对弹性高超声速飞行器,为了实现飞行器的精细姿态控制,采用全状态预设性能控制、全局调节动态神经网络控制以及反演控制方法设计了预设性能精细姿态控制器,本文通过研究分析,得到如下结论: 1)现有文献中都是利用6个弹性模态量来刻画气动弹性,这大大增加了系统的维数,给精细姿态控制带来了巨大的难度,本文优势在于利用已得到证明的诱发攻角概念来刻画气动弹性,将发动机进气口当地攻角看作是飞行器刚体攻角和诱发攻角的和,从而在精细姿态控制器设计中将气动弹性的影响考虑进去。 2)预设性能控制能够兼顾系统的稳态性能和瞬态性能,本文利用预设性能对稳态误差的约束来实现精细姿态控制的指标要求,同时兼顾了系统的瞬态性能,为高超声速飞行器的精细姿态控制提供了一条全新的思路。 3)本文利用全局调节动态神经网络来在线逼近系统的不确定项,与一般的神经网络相比,全局调节动态神经网络的逼近能力更强,适应性更强。 4)在控制器设计过程中,系统的状态跟踪误差e1和e2都实现了预设性能,而不是仅仅考虑系统的输出量满足预设性能,这就实现了系统的全状态满足预设性能。本文利用引理1巧妙地处理了全状态预设性能设计中带来的需要特殊处理的项,为全状态预设性能的应用提供了可行方法。 References) [1] Wu Z G,Yang C. Flight loads and dynamics of flexible air vehicles[J]. Chinese Journal of Aeronautics, 2004, 17(1):17-22. [2] Shaughnessy J D, Pinckney S Z, Mcminn J D, et al. Hypersonic vehicle simulation model: winged-cone configuration, TM-1990-102610 [R]. US: NASA,1990. [3] Clark A D, Wu C, Mirmirani M, et al. Development of an airframe-propulsion integrated generic hypersonic vehicle model[C]∥The 44th AIAA Aerospace Sciences Meeting and Exhibit. Reno, NV, US: AIAA, 2006. [4] Chavez F R, Schmidt D K. Analytical aeropropulsive/aero-elastic hypersonic vehicle with dynamic analysis[J]. Journal of Guidance, Control, and Dynamics, 1994, 17(6):1308-1319. [5] Bolender M A, Doman D B. Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle[J]. Journal of Spacecraft and Rockets, 2007, 44(2):374-387. [6] 张科,崔建峰,吕梅柏.弹性高超声速飞行器多胞鲁棒变增益控制[J]. 西北工业大学学报,2014,32(4):550-555. ZHANG Ke, CUI Jian-feng, LYU Mei-bai. Designing a polytopic robust variable gain controller for flexible hypersonic vehicle[J]. Journal of Northwestern Polytechnical University, 2014,32(4):550-555.(in Chinese) [7] Kuipers M, Mirmirani M, Ioannou P A, et al. Adaptive control of an aeroelastic airbreathing hypersonic cruise vehicle[C]∥ AIAA Guidance, Navigation and Control Conference and Exhibit. SC, US: AIAA,2007: 2007-6326. [8] Sightorsson D O, Jankovsky P, Serrani A, et al. Robust linear output feedback control of an airbreathing hypersonic vehicle[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(4):1052-1066. [9] Xu H J, Mirmirani M, Ioannou P A. Robust neural adaptive control of a hypersonic aircraft[C]∥ AIAA Guidance, Navigation and Control Conference and Exhibit. TX, US: AIAA, 2003: 2003-5641. [10] Wallner E M, Well K H. Nonlinear flight control design for the X-38 using CMAC neural networks[C]∥ AIAA Guidance, Navigation and Control Conference and Exhibit. Montreal , Canada: AIAA , 2001: 2001-4042. [11] 黄显林,逄洪军.考虑气动弹性的高超声速飞行器姿态稳定控制[J].电机与控制学报,2014,18(11): 97-105. HUANG Xian-lin, PANG Hong-jun. Attitude stabilization control of hypersonic vehicle considering aeroelasticity[J]. Electric Machines and Control, 2014,18(11):97-105.(in Chinese) [12] Charalampos P B, George A R. Prescribed performance adaptive control of SISO feedback linearizable systems with disturbances[C]∥The 16th Mediterranean Conference on Control and Automation. Ajaccio, French: IEEE, 2008. [13] Bu X W, Wu X Y, Zhu F J, et al. Novel prescribed performance neural control of a flexible air-breathing hypersonic vehicle with unknown initial errors[J]. ISA Transactions, 2015, 13(7): 125-136. [14] 李海燕,许江宁,张金鹏,等.高超声速飞行器纵向内环系统反演预设性能控制[J].航空兵器,2016,4(2):24-28. LI Hai-yan, XU Jiang-ning, ZHANG Jin-peng, et al.Backstepping control with prescribed performance for longitudinal inner-loop system of hypersonic vehicles[J]. Aero Weaponry, 2016,4(2):24-28.(in Chinese) [15] Parker J T, Bolender M A, Doman D B. Control-oriented modeling of an air-breathing hypersonic vehicle[J]. Guidance , Control, and Dynamics, 2007, 30(3):856-868. [16] Oppenheimer M W, Skujins T, Bolender M A, et al. A flexible hypersonic vehicle model developed with piston theory[C]∥ AIAA Atmospheric Flight Mechanics Conference. CA, US: AIAA, 2007: 1213-1238. [17] 闫杰,于云峰,凡永华,等.吸气式高超声速飞行器控制技术[M].西安:西北工业大学出版社,2014: 24-25. YAN Jie, YU Yun-feng, FAN Yong-hua, et al. Control technology for air-breathing hypersonic vehicle[M]. Xi’an: Northwestern Polytechnical University Press, 2014: 24-25.(in Chinese) [18] Levant A. Higher-order sliding modes,differentiation and output-feedback control[J]. International Journal of Control, 2003, 76( 9/10): 924-941. [19] 胡云安,晋玉强,张友安,等.基于神经网络的严反馈块非线性系统的鲁棒控制[J].控制与决策,2004,19(7): 808-812. HU Yun-an, JIN Yu-qiang, ZHANG You-an, et al. NN-based robust control for strict-feedback block nonlinear systems[J]. Control and Decision, 2004, 19(7):808-812.(in Chinese) [20] 晋玉强.导弹非线性自适应控制系统设计[D].烟台:海军航空工程学院,2003. JIN Yu-qiang. Design of nonlinear adaptive control system for missile[D]. Yantai: Naval Aeronautical Engineering Institute, 2003. (in Chinese) Prescribed Performance Fine Attitude Control for Aeroelastic Hypersonic Vehicle ZHAO He-wei, YANG Xiu-xia, SHEN Ru-song, HU Yun-an (Department of Control Engineering, Naval Aeronautical and Astronautical University, Yantai 264001, Shandong, China) A fine attitude controller for hypersonic cruise vehicle is designed by combining the backstepping technique, prescribed performance control and neural network. The influence of elastic deformation of hypersonic vehicle on angle of attack is taken into consideration. The effect of aeroelasticity on hypersonic vehicle is described by using the induced angle of attack. The index of fine attitude control is satisfied by the design of prescribed performance in consideration of aeroelasticity, and the transient performance of hypersonic vehicle is assured. The unknown terms of the induced angle-of-attack equations are approximated online by using the fully tuned dynamic neural networks, and the adaptive laws of weight, core and scope of influence of the neural networks are designed by Lyapunov theory. The robust term is induced to solve the approximate errors of the neural networks. A fine attitude controller with prescribed performance for hypersonic vehicle in considering the aeroelasticity is designed. The stability of system and all the signals in the closed-loop system bounded are proved by Lyapunov theory. The simulated results show that the controller can make the tracking errors satisfy the prescribed performance, and the fine attitude control can be implemented. ordnance science and technology; hypersonic vehicle; aeroelasticity; prescribed performance; sophisticated attitude control; induced angle of attack 2016-11-11 航空科学基金项目(20155884012) 赵贺伟(1985—), 男, 讲师, 博士研究生。 E-mail:zhwsdyt@163.com 胡云安(1965—), 男, 教授, 博士生导师。 E-mail: hya507@sina.com V249.122+.2 A 1000-1093(2017)03-0501-11 10.3969/j.issn.1000-1093.2017.03.012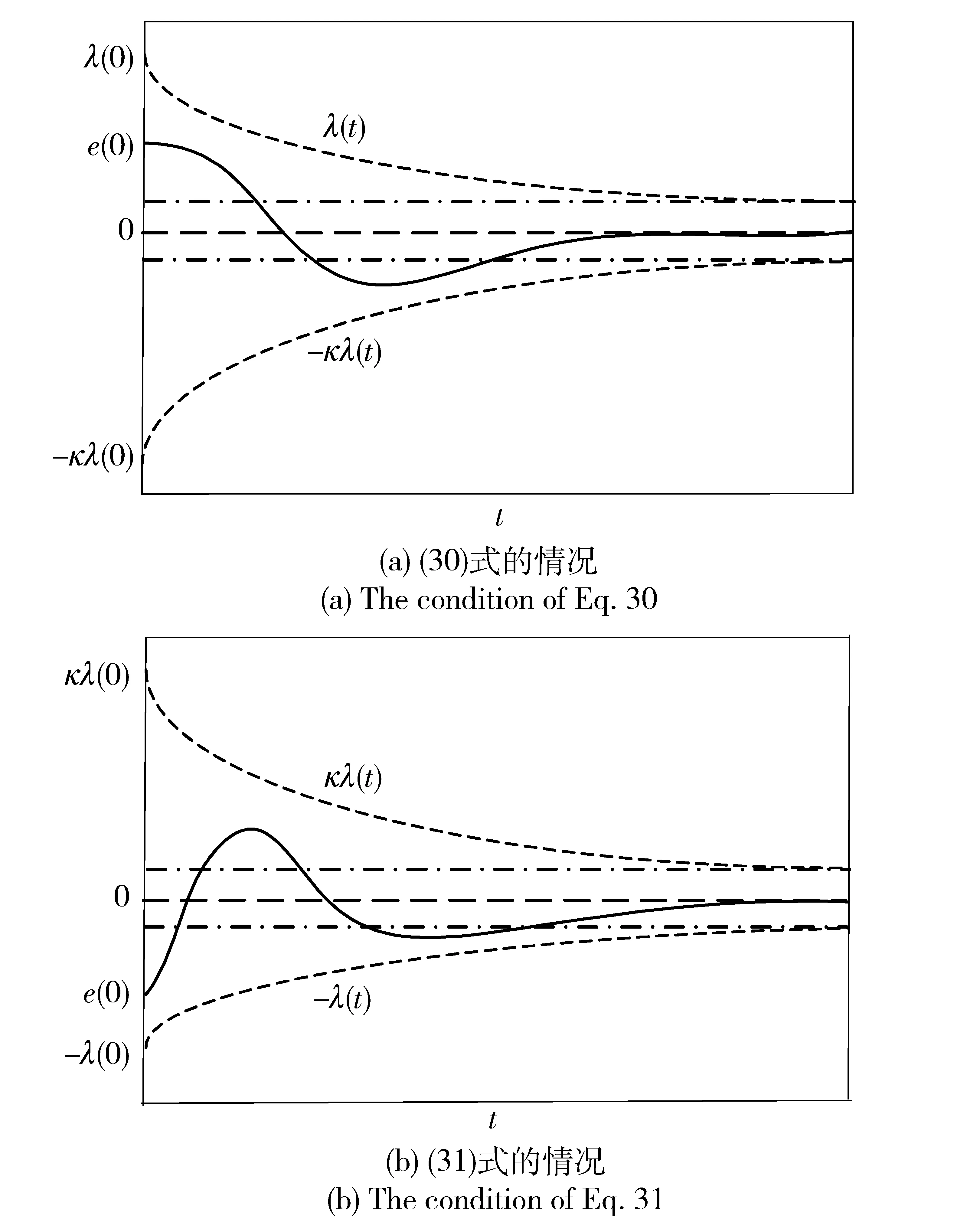

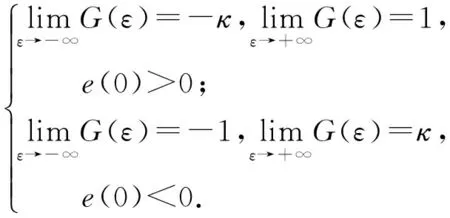
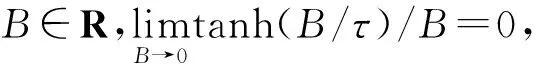
2 控制器设计

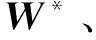

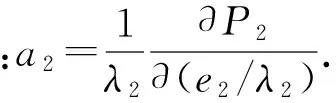
‖′ξ.×‖2+‖′σ.×‖2)/z,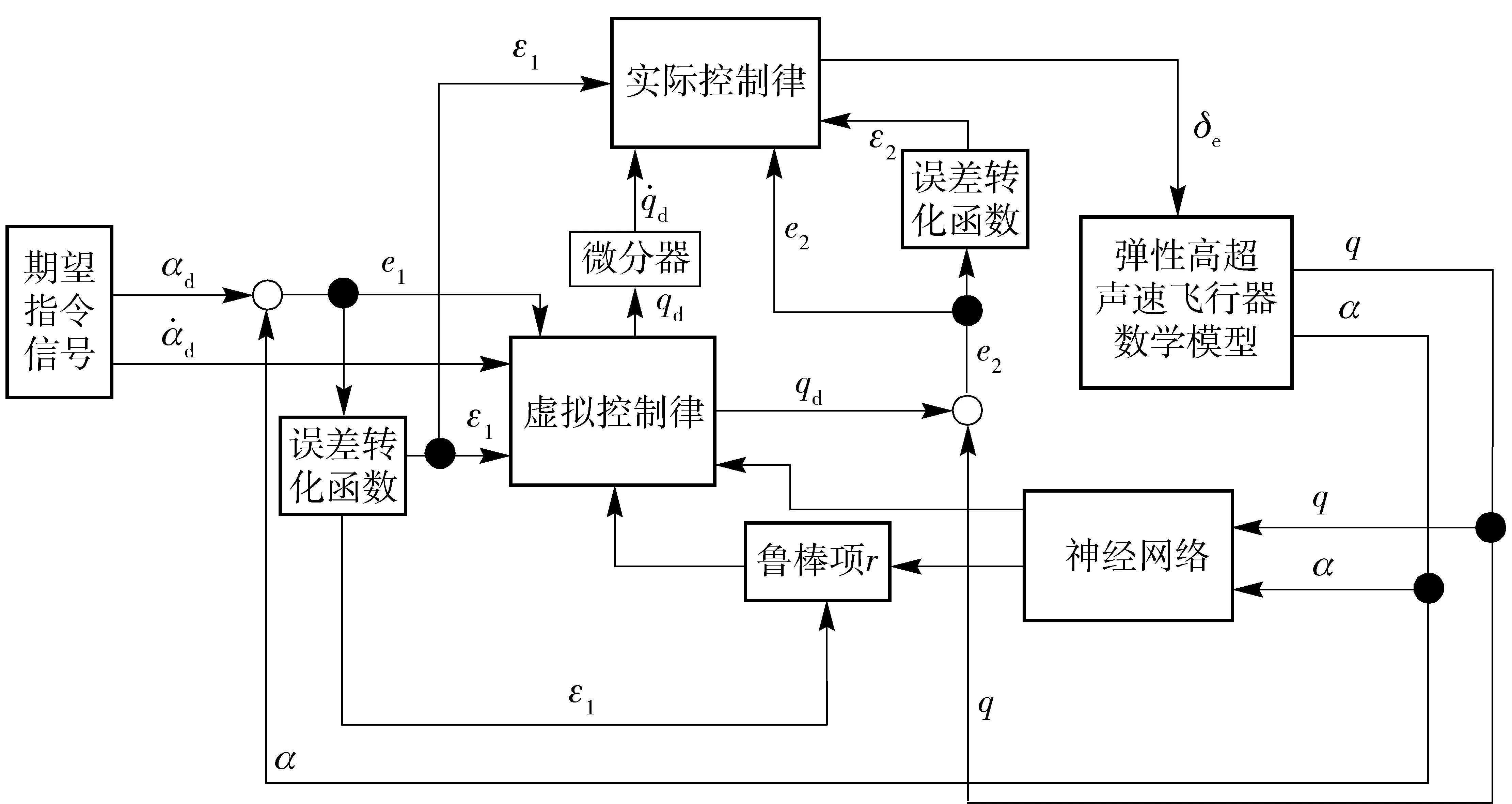
3 仿真分析
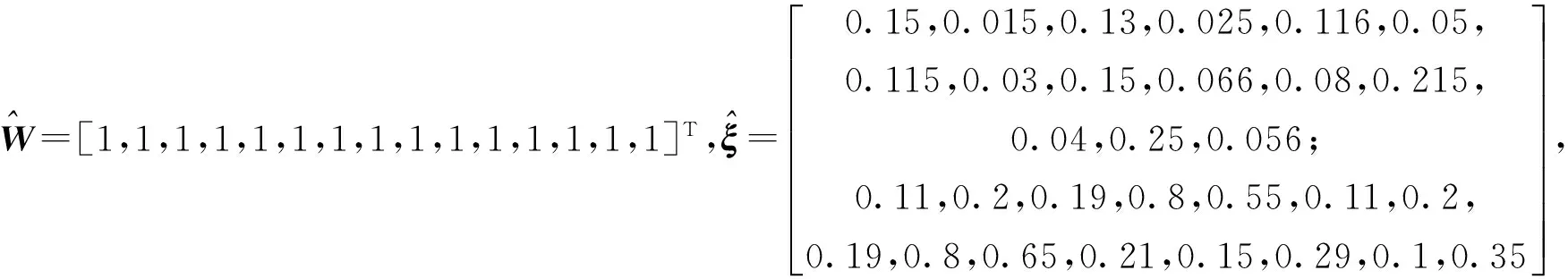




4 结论
