机动管线气顶排空速度的影响因素及作用机理分析

姜俊泽， 张伟明， 雍歧卫， 蒋明

(后勤工程学院 军事供油工程系， 重庆 401331)

机动管线气顶排空速度的影响因素及作用机理分析

姜俊泽， 张伟明， 雍歧卫， 蒋明

(后勤工程学院 军事供油工程系， 重庆 401331)

为提高机动管线的排空速度和机动能力，建立机动管线气顶排空的动力模型，采用特征线法求解，得到清管球速度和管内压力降的变化规律。利用该模型对排空过程进行了计算和实验验证，发现排空速度与空压机流量、压力以及管线的临界长度有关：当管线长度大于临界长度时，空压机的排气量起主要作用，使用大流量的空压机排空速度较快；反之当管线长度小于临界长度时，压力起主要作用，使用大压力的空压机排空速度较快。因此，为提高排空速度，可以在设计时首先计算临界长度，之后根据管线的总长度和临界长度选择性能合适的空压机，或者依据空压机的性能划分排空段的长度。

石油化学工程； 机动管线； 排空； 压力； 流量； 临界长度

0 引言

机动管线是用快装接头连接，地表铺设的一类管线系统，它具有展开、撤收速度快，机动性强的优点，是我军战时油料保障的重要手段。机动管线在改输油品或撤收时要将管内的油品排出并回收，这一过程称为管线的排空，是机动管线使用过程中的一项常规作业。气顶排空作为一种主要的排空方法，具有不受环境条件限制，不需要水源的优点，是高原高寒地区的唯一选择。但由于受限于空压机的性能，对于长达几十公里甚至上百公里的管线，一般不可能实现一次性的全线排空，通常采用分段的方法进行。为了提高排空速度，需要分析排空速度的影响因素，并科学地划分管段长度。而目前对各种因素还没有深入地定量分析，没有得到管段长度同空压机流量和压力的确定关系。管段长度一般是凭经验划分，对于指导排空作业还存在一定的盲目性，制约了气顶排空的应用范围。目前，对于民用固定管线的清管过程研究较多，而对机动管线的气顶排空过程研究得较少。文献[1-2]分析了管道试压排水过程中清管器在不同地形条件下的运动状态，建立了室内管道试压水排放试验系统，并开发了相关软件。金朝文等[3]通过改变阀的开闭时间和迁移空压机的位置来控制输气管线中清管球的运行速度，但并没有对影响清管速度的因素进行深入的定量分析。西南石油大学张琳等[4]建立了油田伴生气管线清管数学模型，该模型能较好地预测清管的始发输气压力，计算结果符合现场实际，具有很强的工程实用性，为清管方案的制定提供了可靠依据。文献[5-6]对气液混输管道清管中清管时间、清管器运行速度等参数进行了数值模拟。Xu等[7]采用混合拉格朗日—欧拉法建立了清管器与气液非稳态流动的耦合模型，并采用有限差分法进行求解，利用该模型可模拟清管器的运行参数和气液两相流量，可用于追踪清管器的运行。郭东升等[8]结合输气管道在线清管作业实际情况，通过建立清管器运动模型，适时控制清管器的运行速度。李长俊等[9]使用多相流模拟OLGA软件对大落差管道内清管器的运行速度和持液率进行了分析，得到了管道所承受的冲击载荷。国外的文献[10-14]也对清管过程进行了研究，但大多也是采用不同的方法建立不同条件下的清管模型，并优选模型中微分方程的数值解法，以提高模型的精度，用来预测清管器运行的速度和位置。Esmaeilzadeh等[15]针对气液两相混输管路建立了清管操作的数学模型，并采用变时步特征线法对模型进行求解，该模型不但可以用来预测清管器的运动速度和清管时间，还可计算出最优的清管流量范围，相比上述的其他模型较为完善。Lesani等[16]建立了小口径管道检测清管器运行的二维和三维模型，可用于清管器在曲线管道运行过程中的速度控制。李涛等[17]利用OLGA软件模拟了管道内积液量、分离器进液量随管道压力和入口气体流量变化的动态过程，得到了合理吹扫方案。清管和排空过程有很多相似之处，但上述的研究成果都没有结合空压机的性能分析影响排空速度的各种因素。本文结合排空作业的工程实际，考虑作业装备的性能，通过建立排空模型，对不同性能空压机的模拟计算，得到压力、流量、排空段长度与排空速度的定量关系。分析各种因素对排空速度的作用机理，为管线的排空作业提供依据，可有效提高排空速度。

1 排空过程的动力模型

排空过程气液之间用清管球隔离，模型如图1所示。图1中Δp为清管器两端压力差，G为清管球所受重力，x为距离，Ff是清管球与液体间的作用力，Fx是气体与清管球间的作用力，Fc为清管球与管壁的摩擦力。

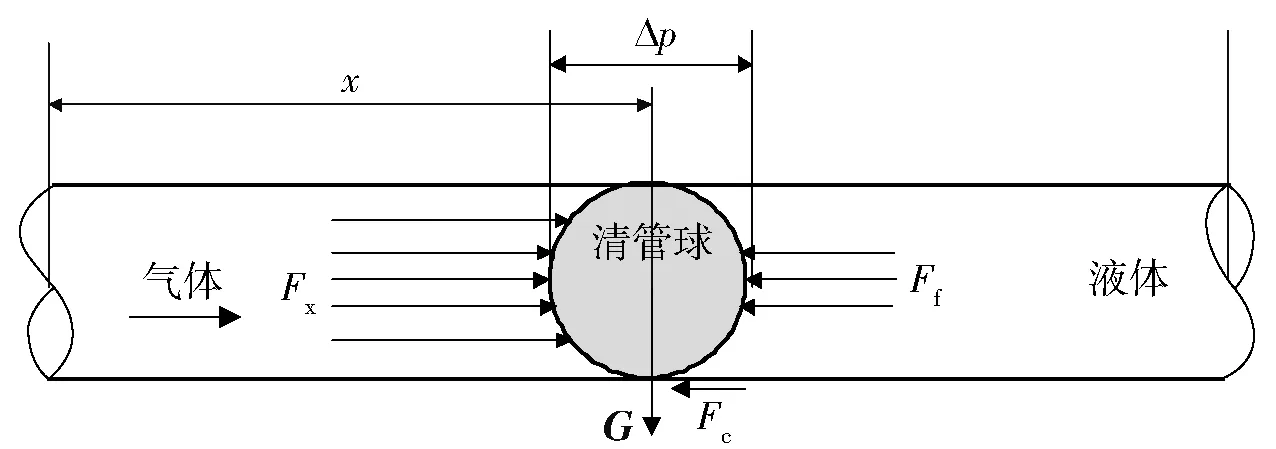
图1 机动管线气顶排空过程Fig.1 Emptying process of mobile pipeline

本文只针对水平管线，根据计算需要和管内流体运动情况，提出如下假设：1)气体为理想气体；2)液体为不可压缩流体；3)气液两相没有质量交换；4)气体和液体被清管器充分隔离；5)等温绝热过程。

对于气体，有连续性方程和动量方程：

(1)

(2)

式中：pG为气体压力；uG为气体速度；ρG为气体密度；t为时间；A为管道截面积。

考虑气体的可压缩性，需要实际气体的状态方程和压力波表达式：

pGVG=ZRGT，

(3)

(4)

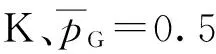
由于在实际排空过程，使用的是空压机，而不是体积无限大的具有恒定压力和流量的气源， 需要引入空压机的性能方程[19]：

p=a-b(AuG)2，

(5)

式中：a、b为待定系数，可通过拟合得到。

对于液体有连续性方程和动量方程：

(6)

(7)

式中：pL是液体压力；uL是液体速度；ρL是液体密度。

清管球的运动是靠其上下游的压差驱动的，清管球的运动方程可表示为：

(8)

式中：mp为清管球的质量；vp是清管球的速度，其计算方法见文献[20]。

2 模型的求解

将(1)式和(2)式写成向量的形式：

(9)

式中：

W=[ρuGp]T；

(10)

(11)

通过分析A′方程的特征根可知，矩阵A′的特征值就是(9)式的特征值。矩阵A′方程的特征值为

(12)

用A′的特征向量左乘(10)式可以得到相容性方程：

[Li]T[Wt+A′Wx]=0，

(13)

式中：Li为矩阵A′的特征向量，

L1=[01c/p]，

(14)

L2=[01-c/p]；

(15)

Wt为W的时间变量；Wx为W的位置变量。

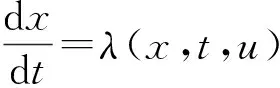
(16)

(17)

式中：

(18)

(19)

变量pG、ρG、uG在P点(见图2)的值可以通过计算网格点L、N、O得到，而在网格结点R、M、S的值可以通过线性插值公式得到。图2给出了变量pL、ρG、uG在两个相邻时步间的关系。

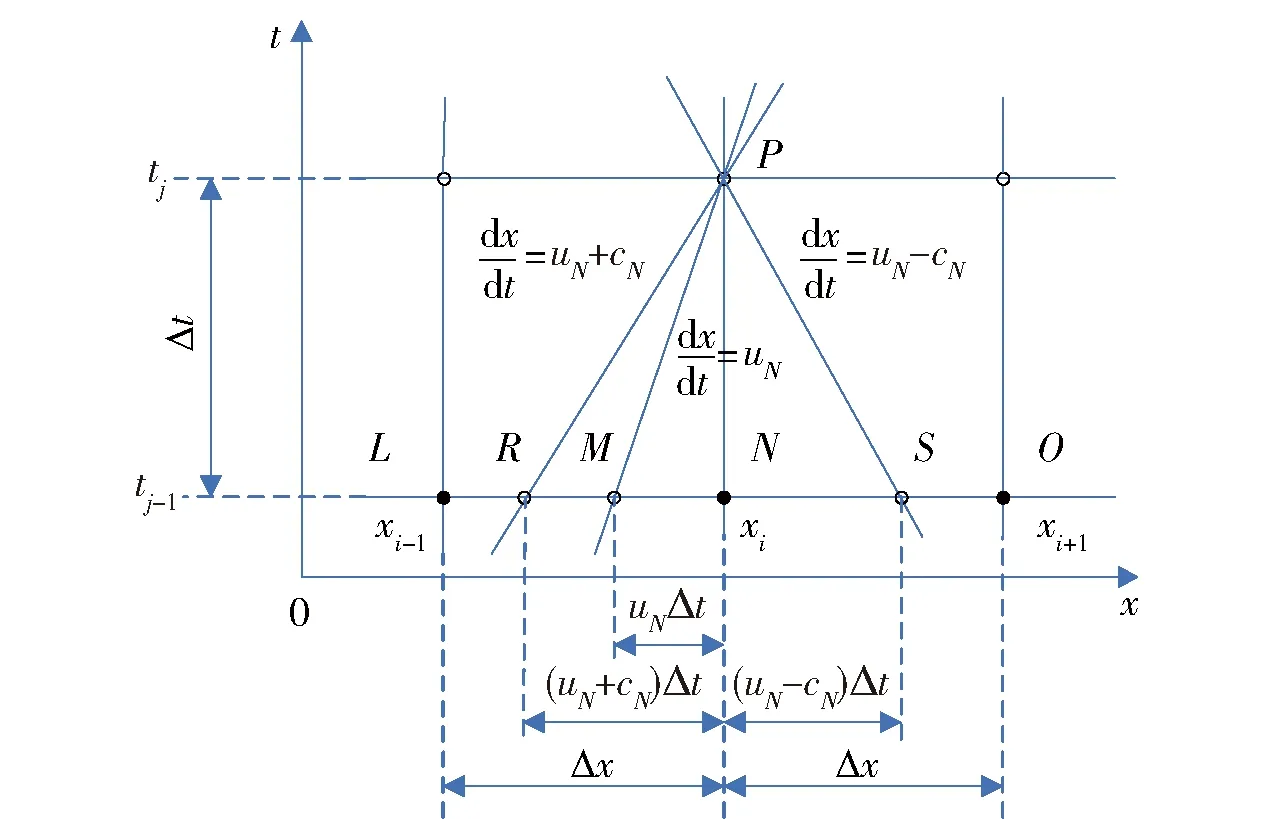
图2 气体方程的特征线算法Fig.2 Backward and forward MOC algorithm for gas flow

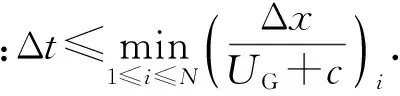
(16)式和(17)式可沿相应的特征线进行积分得到求解变量。由线性插值，可得

(20)

(21)

式中：X代表不同时刻的结点上的pL、ρG、uG.

由(20)式～(21)式可得

(22)

(23)

由(23)式可以得到：

(24)

液体方程的求解方法与气体方法相同，其中：

(25)

(20)式～(25)式中，下标R、M、S代表各变量在R、M、S各点的插值。

将(22)式和(25)式代入(8)式，可得到任意时刻清管球速度vp和管内压力p.

3 不同压力流量下的排空速度对比

为考察不同初始条件对排空速度的影响，将初始条件分别设为：1)工作压力为0.7 MPa，排气量为10 m3/min，代表A型空压机；2)工作压力为1.0 MPa，排气量为7 m3/min，代表B型空压机。空压机的性能方程可通过最小二乘法拟合得到：

pA=2-0.033Q+0.000 16Q2,

(26)

pB=(3-1.45Q)1.24,

(27)

式中：Q为空压机流量。

同时考虑管长的影响，将管长设为3 000 m和5 000 m分别进行计算。

根据特征线解法，分别计算求得两种不同工况下气体方程和液体方程的特征根分别为

工况1：气体方程的特征根为：λG1=9，λG2=-331，λG3=349；液体方程的特征根为：λL1=3，λL2=-1 377，λL3=1 383.

工况2：气体方程的特征根为：λG1=14，λG2=-326，λG3=354；液体方程的特征根为：λL1=5，λL2=-1 375，λL3=1 385.

运行参数的计算结果如图3所示。

图3 两型空压机的排空速度对比Fig.3 Comparison of draining rates of two air compressors

图3是清管球速度- 时间曲线，图3(a)排空段长度(管长)为3 000 m，图3(b)排空段长度为5 000 m. 由于两型空压机均在额定转速下工作，因此可以达到它们的额定压力和排气量。由图3可见：当管长为3 000 m时，B型空压机的排空速度始终高于A型空压机；当管长为5 000 m时，开始时B型空压机的速度大于A型空压机，但随着排空的进行，速度差距逐渐变小，但当排空进行到580 s时，A型空压机和速度超过了B型空压机。由此可见，压力较大的空压机在排距较短或排空的初始阶段有较大的速度，而当管长达到一定程度以后，流量较大的空压机更有优势。

为进一步分析排空速度的影响因素，对比上述条件下的管内压力变化情况，如图4所示。

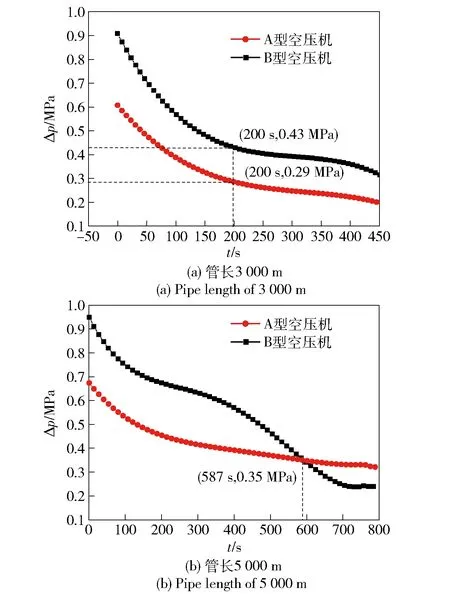
图4 两型空压机的清管压降对比Fig.4 Comparison of pressure drops of two air compressors

图4是排空过程管内的压降- 时间曲线，当管长为3 000 m时，使用B型空压机的管内压力始终高于A型空压机，但管内的压降差别不大，截至200 s时，两种工况下的压降分别为0.43 MPa和0.29 MPa. 当管长为5 000 m时，在587 s以前，使用B型空压机的管内压力高于A型空压机；但在587 s之后，B型空压机的管内压力则低于A型空压机，总体来看B型空压机的管内压力下降幅度大于A型空压机；在800 s时，B型空压机的管内压降比A型低0.079 MPa. 可见在管段较短时，B型空压机优势明显，但在管段较长时，A型空压机比B型空压机能更好的维持管内压力。

由对比可知，管线的排空速度与空压机的流量、压力以及排空段的长度有关。排空段较短时，压力起主要作用；排空段较长时，排气量起主要作用。原因在于，排空开始时，管内液体较多，需要足够大的压力推动液体运动，较大的压力可以使管内流速度迅速增加，并维持在较高水平，这时压力起主要作用；但排空过程气体和液体的速度是不同的，气体和液体的速度由前者大后者小逐渐转变为前者小后者大，当液体速度超过气体速度的时候，管内压力将会下降，这是由于排气量不足导致的，可见压力的建立和保持需要有足够的气体流量，较大的排气量可以使管内压力维持在较高的水平。或者说，排气压力是决定排空速度的根本原因，而排气量是建立压力的必要条件，它通过对管内压力的积累影响排空速度。因此，对于排空过程存在一个压力和流量作用的临界长度，这个临界长度与排空段长度和排空时间有关，下面通过计算来确定这一临界长度。

4 临界长度的确定

由于排空过程管内的清管球或是液体流速为变加速直线运动，因此临界长度可表示为

(28)

利用模型分别代入两种工况下的初始条件并假设管线无限长，得到工况1下清管球的运动速度方程：

vp1(t)=-0.132+0.013 53t-5.443 9×10-5t2+
6.425 7×10-8t3+1.447 6×10-24t4.

(29)

工况2下清管球的运动速度方程：

vp2(t)=0.129+0.116t-4.13×10-5t2+
4.539 73×10-8t3-5.161×10-26t4.

(30)

联解(29)式和(30)式得到时间t1=557.5 s，代入(28)式得到临界长度Lc=4 357.6 m.

也就是说当排空段长度大于4 357.6 m时，应使用A型空压机，而在排空段长度小于4 357.6 m时，应使用B型空压机。当然，这一临界长度是在两种特定工况下得到的，对于具有不同额定流量和压力的空压机，临界长度会有所变化。下面再以一个算例进行分析说明。

图5 C、D两型空压机的排空速度对比Fig.5 Comparison of draining rates of C and D air compressors

还是选择具有不同压力和流量的空压机进行对比：一种C型空压机，压力是1.5 MPa，流量是10 m3/min；另一种D型空压机，压力是0.7 MPa，流量是20 m3/min. 假设管长是8 km，采用上述模型进行计算，得到的临界长度为Lc=6 863.2 m，临界时间t=719.8 s，清管球的速度曲线如图5所示，管内压力降如图6所示。

图6 C、D两型空压机的排空压降对比Fig.6 Comparison of pressure drops of C and D air compressors

由图5可见，对于具有不同压力和排气量的空压机，上述结论同样适用，只是临界长度的时间有所不同，而且从图6也可看出，管内的压力降在临界时间719.8 s之后D型空压机也超过了C型空压机，进一步验证了上述结论的正确性。因此，为提高排空速度，要根据排空段长度选择性能合适的空压机，或者依据空压机的参数划分排空段长度，可以采用上述模型进行临界长度的计算，为排空设计提供依据。

5 实验验证

5.1 实验设计

为验证上述模型的准确性，铺设了DN100机动管线对不同压力流量下的排空时间进行了实测，实验流程见图7.

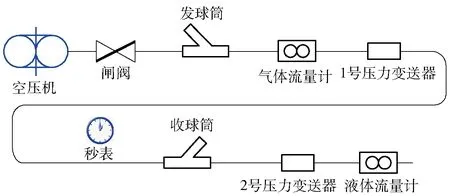
图7 实验流程图Fig.7 Flow chat of experiment

实验中所用的空压机为滑片式空压机，其最大排气压力为0.7 MPa，最大排气量为10 m3/min，其内设置稳压罐，出口有压力调节阀，可通过改变发动机转速调整其排气量。两个清管器收发装置之间的距离为5 000 m，清管器收发装置上带有指示器，可以准确判断清管器到达时间。

5.2 实验数据分析

为验证模型计算的准确性，将模型的计算值和现场实验值进行比较，结果如图8和图9所示。

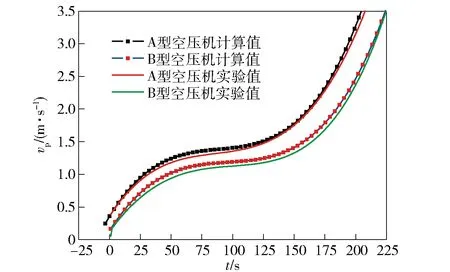
图8 A、B型空压机的清管球速度计算值与 实验值对比Fig.8 Comparison between calculated value and experimental value on spherical pig velocities of A and B air compressors

图9 A、B型空压机的管内压力降计算值与实验值对比Fig.9 Comparison between calculated value and experimental value on pressure drops of A and B air compressors

由图8可见，在对清管球的速度进行预测时，模型计算值与实验值吻合良好，只是0～150 s间，模型的计算值略高于实验值，但对于模型计算的准确性影响不大。由图9可见，在对管线压力降的预测时，计算值与实验值的变化趋势基本相符。只是对于A型空压机的计算，在300 s后，计算值略偏离实验值，在研究过程中对这一现象经过多次的实验对比，此现象一直存在，可能是由于实验中的清管球与管壁摩擦使其发生形变而引起的管内压力升高。综合来看，该模型计算的准确性较好，与实验数据基本吻合。

此外，为了分析临界长度的变化规律，调整了空压机的工况，进行不同压力和排气量下的排空速度实验，数据见表1和表2.

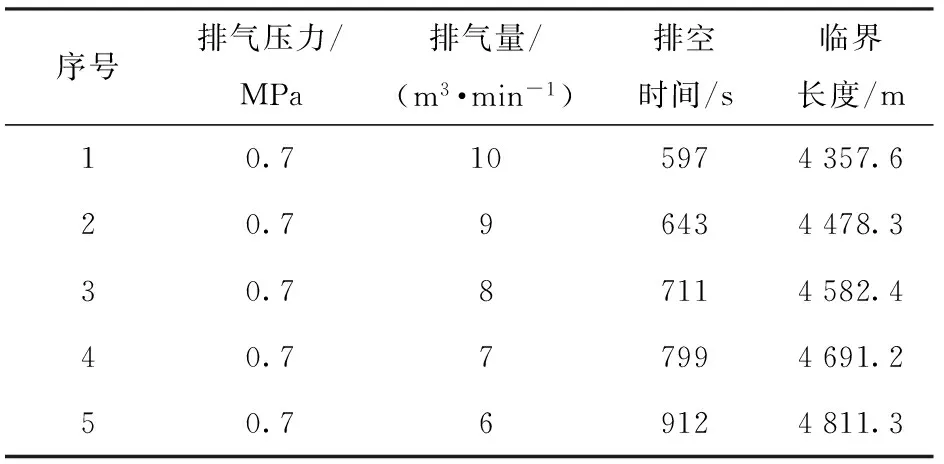
表1 相同排气压力下排空时间实测数据Tab.1 Emptying time at the same gas pressure

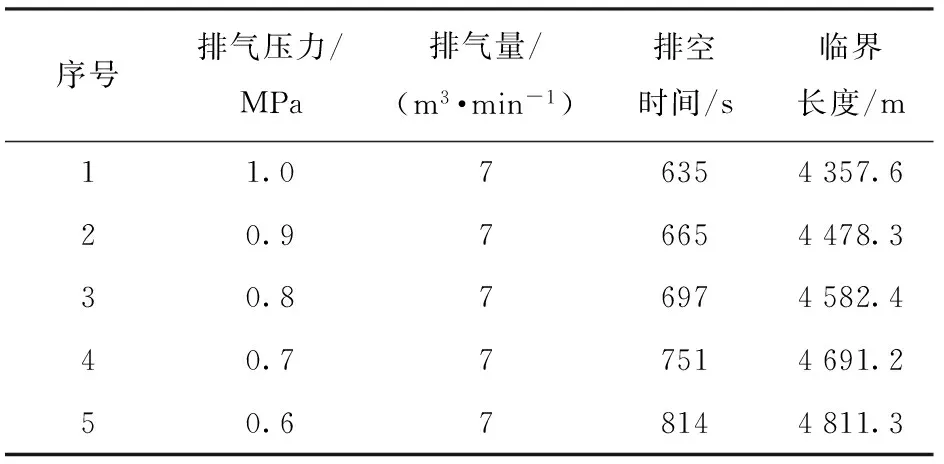
表2 相同排气量下排空时间实测数据Tab.2 Emptying time at the same gas flow rate

通过表1和表2的实验数据可见，模型对于排空时间的预测较为准确，在排空段长度超过临界长度的情况下，当排气压力不变而排气量减小，或者当排气量不变而排气压力减小时，排空时间都要增加，且前者需要的时间更长。

6 结论

通过建立机动管线的气顶排空模型，得到了清管球的速度随时间的变化规律。

1)在进行排空作业时，排空速度与空压机的排气量、压力以及管线的长度有关，排空段较短时，压力起主要作用，排空段较长时，排气量起主要作用。

2)为提高排空速度，可采用临界长度作为空压机选型的依据，当管线长度超过临界长度时，使用大排气量的空压机可以获得较快的排空速度，而当管线长度小于临界长度时，使用大压力的空压机可以获得较快的排空速度。

3)通过试算发现，当管线长度增加时，临界长度和临界时间也会增加，而当空压机的排气量和排气压力增加时，临界长度和临界时间则相应地减小。因此，在进行排空作业时，要根据排空段长度选择性能合适的空压机，或者依据空压机的参数划分排空段的长度，从而提高作业效率。

References)

[1] 邓涛, 宫敬, 于达, 等. 复杂地形对长距离输气管道试压排水的影响[J]. 油气储运, 2014, 33(12):1326-1330. DENG Tao, GONG Jing, YU Da, et al. Influence of complex terrain on the pressure test and drainage of long-distance gas pipeline[J]. Oil & Gas Storage & Transportation, 2014, 33(12):1326-1330.(in Chinese)

[2] 邓涛, 肖斌涛, 于达, 等. 油气管道试压水排放试验系统[J]. 油气储运, 2015, 34(12):1305-1309. DENG Tao, XIAO Bin-tao, YU Da, et al. Test system for water draining after hydrotest of oil/gas pipelines[J]. Oil & Gas Storage & Transportation, 2015, 34(12):1305-1309.(in Chinese)

[3] 金朝文. 输气管道清管球速度控制[J]. 天然气与石油, 2009, 29(1):31-35. JIN Chao-wen. Speed control of pig in gas pipe[J]. Natural Gas and Oil, 2009, 29(1):31-35.(in Chinese)

[4] 张琳, 李长俊, 刘春江, 等. 油田伴生气管线清管模型研究[J]. 天然气工业, 2006, 26(8):120-122. ZHANG Lin, LI Chang-jun, LIU Chun-jiang, et al. Research on pigging model for the associated gas pipeline[J]. Natural Gas Industry, 2006, 26(8):120-122.(in Chinese)

[5] 李玉星, 寇杰, 唐建峰, 等. 多相混输管路清管技术研究[J]. 石油学报, 2002, 23(5):101-105. LI Yu-xing, KOU Jie, TANG Jian-feng, et al. Experiment study of pigging techinology for multiphase flow in pipelines[J]. Acta Petrolei Sinica, 2002, 23(5):101-105.(in Chinese)

[6] 丁浩, 李玉星, 冯叔初. 水平气液混输管路清管操作的数值模拟[J].石油学报, 2004, 25(3):24-27. DING Hao, LI Yu-xing, FENG Shu-chu. Pigging operation simulation for horizontal flow of gas and liquid in pipeline[J]. Acta Petrolei Sinica, 2004, 25(3):24-27.(in Chinese)

[7] Xu J Y, Li C J, Liu B, et al. Numerical simulation of pigging operation in gas-liquid two-phase flow pipelines[C]∥2011 International Conference on Pipelines and Trenchless Technology. Beijing: Pipeline Division of ASCE, 2011:477-491.

[8] 郭东升, 闰青松, 徐麦玲. 长输天然气管道在线清管作业运行速度控制[J]. 油气储运, 2013, 32(2):1330-1335. GUO Dong-sheng, RUN Qing-song, XU Mai-ling, et al. Control of on-line pigging operation speed for long-distance gas pipeline[J]. Oil and Gas Storage and Transportation, 2013, 32(2):1330-1335.(in Chinese)

[9] 李长俊, 刘希尧, 贾文龙, 等. 大落差天然气管道清管冲击分析[J].油气田地面工程, 2015, 34(12):46-48. LI Chang-jun, LIU Xi-yao, JIA Wen-long, et al. Analysis of pigging impact on large falling natural gas pipeline[J]. Oil-Gas Field Surface Engineering, 2015, 34(12):46-48. (in Chinese)

[10] Nguyen T T, Kim S B. Modeling and simulation for PIG flow control in natural gas pipeline[J]. KSME International Journal, 2001, 15(8):1165-1173.

[11] Nguyen T T, Kim D K, WooPho Y, et al. Dynamic modeling and its analysis for PIG flow through curved section in natural gas pipeline[C]∥2001 IEEE International Symposium on Computational Intelligence in Robotics and Automation. Banff, Alberta, Canada:IEEE, 2001.

[12] Hosseinalipour S M, Khalili A Z, Salimi A, et al. Numerical simulation of pig motion through gas pipelines[C]∥16th Australasian Fluid Mechanics Conference. Gold Coast, QLD, Australia: University of Queenoland, 2007.

[13] Tolmasquima S T, Nieckele A O. Design and control of pig operations through pipelines[J]. Journal of Petroleum Science and Engineering, 2008, 62(3):102-110.

[14] Saeidbakhsh M, Rafeeyan1and S M, Ziaei Rad. Dynamic analysis of small pigs in space pipelines[J]. Oil & Gas Science and Technology, 2009, 64(2):155-164.

[15] Esmaeilzadeh F, Mowla D, Asemani M. Mathematical modeling and simulation of pigging operation in gas and liquid pipelines[J]. Journal of Petroleum Science and Engineering, 2009, 69(1):100-106.

[16] Lesani M, Rafeeyan M, Sohankar A. Dynamic analysis of small pig through two and three-dimensional liquid pipeline[J]. Journal of Applied Fluid Mechanics, 2012, 5(2):75-83.

[17] 李涛,宗媛,朱德闻.基于OLGA软件的湿气管道清管动态分析[J].油气储运,2016,35(5):526-529. LI Tao, ZONG Yuan, ZHU De-wen.Dynamic analysis of pigging operation in wet gas pipeline by OLGA[J]. Oil & Gas Storage and Transportation,2016,35(5):526-529.(in Chinese)

[18] 王树立. 输气管道设计与管理[M]. 北京:化学工业出版社, 2006. WANG Shu-li.Gas pipeline design and Management[M]. Beijing:Chemical Industry Press, 2006.(in Chinese)

[19] 沙毅, 闻建龙. 泵与风机[M]. 合肥:中国科学技术大学出版社, 2008. SHA Yi, WEN Jian-long. Pumps and fans[M]. Hefei: University of Science and Technology of China Press,2008. (in Chinese)

[20] 姜俊泽. 机动管线排空特性与气液混合物形成机理实验研究[D]. 重庆:后勤工程学院, 2013. JIANG Jun-ze. Experimental study on mobile pipeline emptying characteristics and mechanism of gas-liquid mixture formation[D]. Chongqing: Logistical Engineering University, 2013. (in Chinese)

Analysis of the Influencing Factors and Mechanism of Gas Draining Rate of Mobile Pipeline

JIANG Jun-ze, ZHANG Wei-ming， YONG Qi-wei, JIANG Ming

(Department of Oil Supply Engineering, Logistics Engineering University, Chongqing 401331, China)

In order to promote the emptying efficiency of mobile pipeline, a dynamic model of emptying is established, which is solved by the method of characteristics (MOC), and the velocity of spherical pig and the variation of pressure drop are obtained. The model was verified by experiments. The emptying rate is related to the critical length of pipeline, the gas flow rate and max pressure of compressor. If the length of pipeline is longer than its critical length, the gas flow rate plays a dominant role in the emptying rate, and a high-flow-rate compressor should be used. On the contrary, if the length of pipeline is shorter than its critical length, the gas pressure plays a dominant role, and a high-pressure compressor should be used. The critical length increases with the development of pipe length, while the critical length decreases with the development of gas flow rate and pressure. Hence, in order to promote the emptying efficiency, the critical length should be determined in the design, and then an appropriate compressor is chosen in terms of the overall length and critical length of pipeline or the length of emptying segment is partitioned according the compressor performance.

petrochemistry engineering; mobile pipeline; emptying; pressure;flow rate;critical length

2016-05-24

姜俊泽(1984—)，男，讲师，博士。E-mail: 154950688@qq.com

E234

A

1000-1093(2017)03-0585-08

10.3969/j.issn.1000-1093.2017.03.023