捷联导引头寄生回路分析及其品质测试研究

白瑞， 夏群利， 杜肖， 鲁天宇，2

(1.北京理工大学 宇航学院， 北京 100081；2.北京理工大学 机电学院， 北京 100081)

捷联导引头寄生回路分析及其品质测试研究

白瑞1， 夏群利1， 杜肖1， 鲁天宇1，2

(1.北京理工大学 宇航学院， 北京 100081；2.北京理工大学 机电学院， 北京 100081)

为研究隔离度寄生回路对捷联图像导引头的影响，建立了捷联导引头隔离度寄生回路模型。通过无量纲化后得到无量纲特征方程，利用劳斯判据研究了制导参数、陀螺和探测器的刻度尺偏差和动力学偏差对稳定域的影响，并分析寄生回路对制导动力学的影响，建立非线性仿真模型；利用蒙特卡洛法研究脱靶量随刻度尺偏差和动力学偏差的变化规律，建立了半实物开环仿真测试系统，对隔离度寄生回路品质进行了评价。研究结果表明：角速率陀螺与探测器之间的刻度尺误差和动力学不匹配是引起隔离寄生回路的主要因素，其差值的正负分别代表隔离度寄生回路反馈的正负特性；正反馈的稳定域要远小于负反馈的稳定域，并且脱靶量对制导系统偏差的敏感度更大；为了提高系统阻尼，提高导弹末制导精度，需采用五轴转台半实物仿真测试系统对隔离度寄生回路的阻尼特性进行测试标定，或者消除刻度尺误差，完成动力学匹配，进而消除寄生回路的影响，或者构造负反馈寄生回路以减弱其影响。

兵器科学与技术； 捷联导引头； 寄生回路； 刻度尺偏差； 动力学偏差； 半实物测试

0 引言

隔离度作为导引头的一项重要指标，显示了导引头隔离弹体扰动的能力[1-2]，直接关系到导弹的制导精度。隔离度引起的制导寄生回路会降低制导回路的稳定性，严重影响导弹的飞行品质[3-5]。

与传统框架式导引头相比，捷联导引头取消了机械回转结构，使导引头体积、成本大幅降低，可靠性提高，跟踪速度和跟踪精度不受机械限制和摩擦力矩的影响[6-7]，这使捷联导引头的应用受到越来越多的关注。但捷联导引头具有固有缺陷[8]，首先捷联导引头加大了瞬时视场，因导引头量测误差与瞬时视场大小成正比，这使得捷联导引头量测误差很大；其次捷联导引头需利用探测器信息和惯导量测信息进行数学解耦，探测器和惯导的量测误差、刻度尺和动力学不一致都会产生隔离度。

目前国内外关于隔离度寄生回路的研究主要围绕平台导引头展开，Williman等[9]和Garnell等[10]对由于天线罩误差斜率产生的寄生回路进行研究。崔莺莺等[1]对平台导引头隔离产生机理及隔离度模型进行研究，提出了干扰力矩是产生隔离度的主要原因。杜运理等[2]进一步研究了隔离度寄生回路的形成原理，并深入研究了隔离度相滞后对寄生回路稳定性的影响。宋韬等[11]对平台导引头隔离度两种物理模型进行研究，提出了基于惯性系的隔离度模型。李富贵等[12]、朱华征等[13]对平台导引头隔离度及隔离度寄生回路测试方法进行研究，得到了可用于工程实践的测试流程。国内学者鄢琴涛等[14]、李富贵等[15]对捷联导引头隔离度指标工程计算方法进行了研究，建立了基于脱靶量的隔离度指标分析体系。但是总体而言，国内外对于捷联导引头隔离度寄生回路的研究较少，特别是针对捷联导引头寄生回路分析及其品质测试的研究有限。

本文针对捷联红外成像导引头，为深入研究隔离度寄生回路对捷联导引头的影响，建立了导引头隔离度寄生回路模型，分析了刻度尺偏差和动力学偏差以及制导参数对捷联导引头隔离度寄生回路稳定性以对脱靶量的影响，提出了基于半实物仿真测试系统的隔离度寄生回路品质评价方法，所得结论将为导弹总体方案初步设计提供理论参考。

1 隔离度寄生回路模型

(1)

作拉普拉斯变换，则隔离度传递函数可表示为

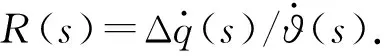
(2)

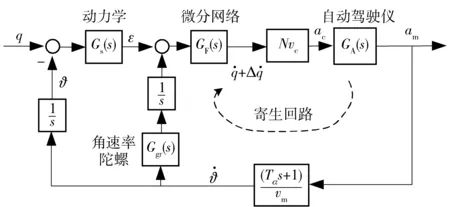
图1 平台导引头隔离度模型Fig.1 Model of disturbance rejection rate of seeker

从图1可得隔离度传递函数为

(3)

制导回路动力学传函为

(4)

式中：Ts为探测器动力学时间常数；Tgr为角速率陀螺时间常数；TF为制导滤波器时间常数；TA为驾驶仪时间常数；ks为探测器刻度尺；kgr为角速率陀螺刻度尺。则

(5)

定义刻度尺偏差：

k=kgr-ks.

(6)

定义动力学无量纲偏差：

(7)

结合(4)式和(5)式可知，隔离度寄生回路的特性受探测器和陀螺刻度尺偏差和动力学偏差的共同影响，下面分别对刻度尺偏差和动力学偏差的影响进行研究。为了便于后续分析，在不存在动力学偏差时分别取参数如表1所示。表1中Tg为导弹制导时间常数。

表1 典型参数表Tab.1 Typical parameters

2 刻度尺偏差的影响

令Ts=Tgr=Tg/5，此时系统不存在动力学偏差，只存在刻度尺偏差，代入(3)式：

(8)

把(8)式代入(4)式，有

(9)

从(9)式可知：k>0时，隔离度寄生回路为正反馈回路；k<0为负反馈。为便于分析，采用时间尺度无量纲化方法对寄生回路进行无量纲化处理，令

(10)

将(10)式代入(9)式得系统特征方程：

(11)

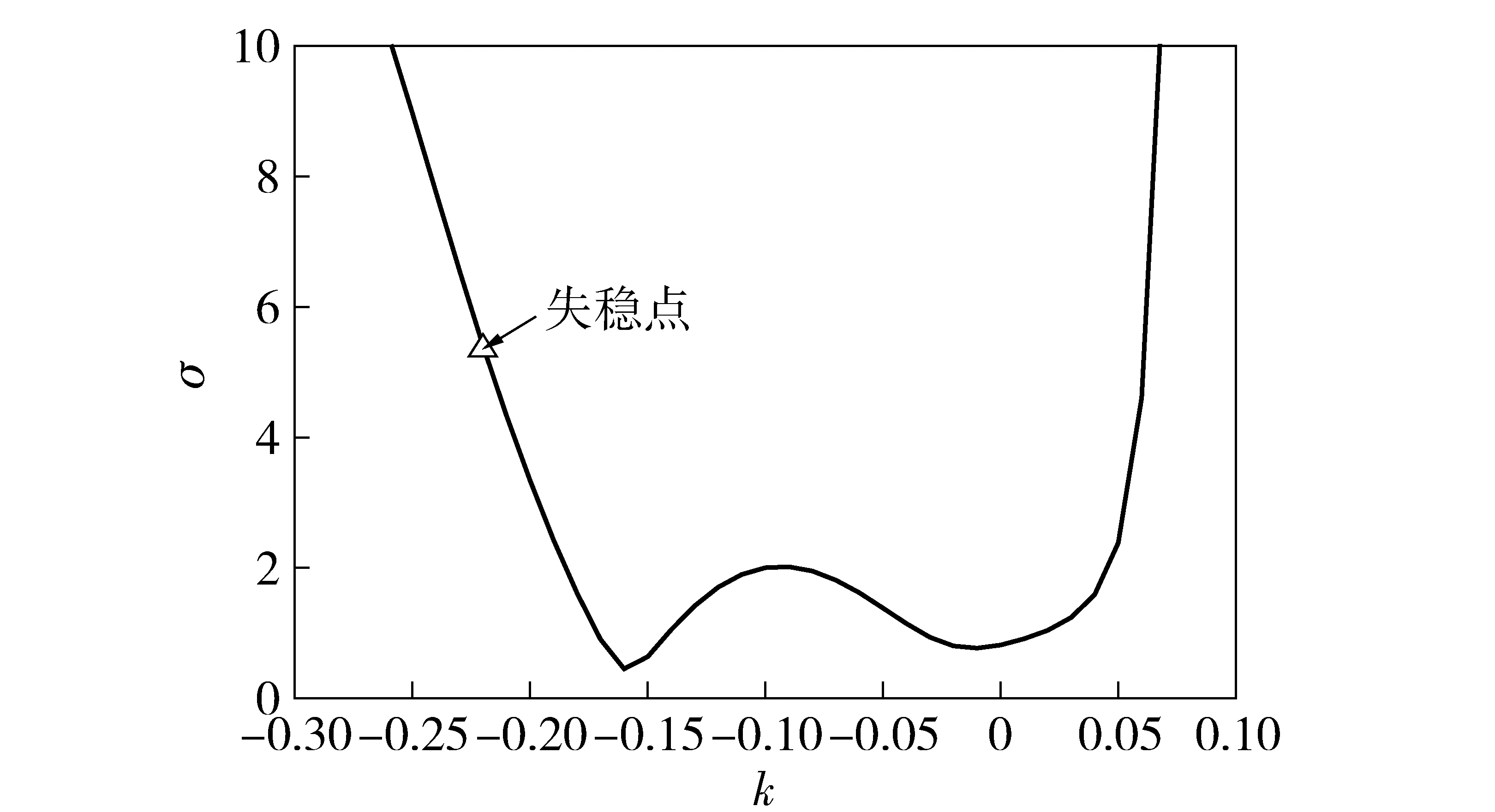
从图2可知，隔离度正反馈时寄生回路稳定域要远小于负反馈时的稳定域；随着|k|增大，寄生回路稳定域会逐渐减小；增大比例导引系数N和vc/vm都会减小稳定域；攻角时间常数Tα的增加或制导系统时间常数Tg的减小都会缩小稳定域。弹上高精度惯导系统中角速率陀螺的刻度尺kgr波动范围很小，刻度尺偏差主要由多元探测器的刻度尺ks波动引起，因此在飞行过程中要对探测器刻度尺进行误差补偿，保证刻度尺偏差为0或满足负反馈条件。

图2 刻度尺偏差对寄生回路稳定性的影响Fig.2 Effect of scale factor error on stability of parasitical loop

对(9)式进行等价：

(12)

式中：Neff为等效有效导航比，Teff为等效制导系统时间常数，

(13)

从(13)式可知，k负值会降低等效有效导航比，但会使制导系统时间常数增大；而k正值所起作用正好相反。取典型参数N=3，vc/vm=1，Tα/Tg=3，图3给出了制导系统主根阻尼ζ随k变化曲线，图4给出了制导系统闭环阶跃响应曲线。由图3可知，主根阻尼ζ随k增大而迅速减小，正反馈时阻尼下降速度比负反馈快。从图4可知，刻度尺偏差对动力学的改变与用(13)式的分析结论一致，k正值使系统稳态增益增加，响应时间减小，但ζ的下降使系统剧烈震荡，k负值使系统稳态增益减小，响应时间增加。

图3 主根阻尼随刻度尺偏差增大而变小Fig.3 Damping vs. scale factor error

图4 刻度尺偏差对系统动力学的影响Fig.4 Effect of scale factor error on system’s dynamics

3 动力学偏差的影响

令ks=kgr=1，使系统无刻度尺偏差，只存在动力学偏差，代入(4)式得

(14)

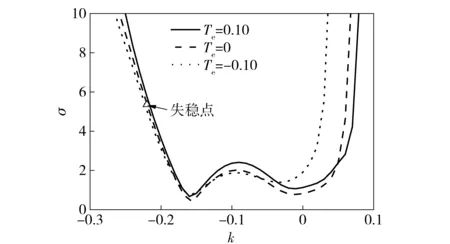
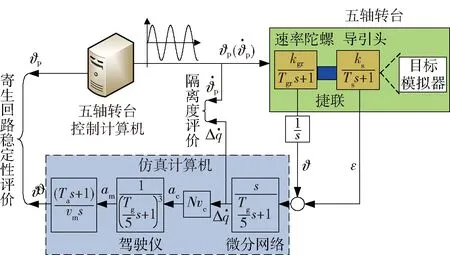
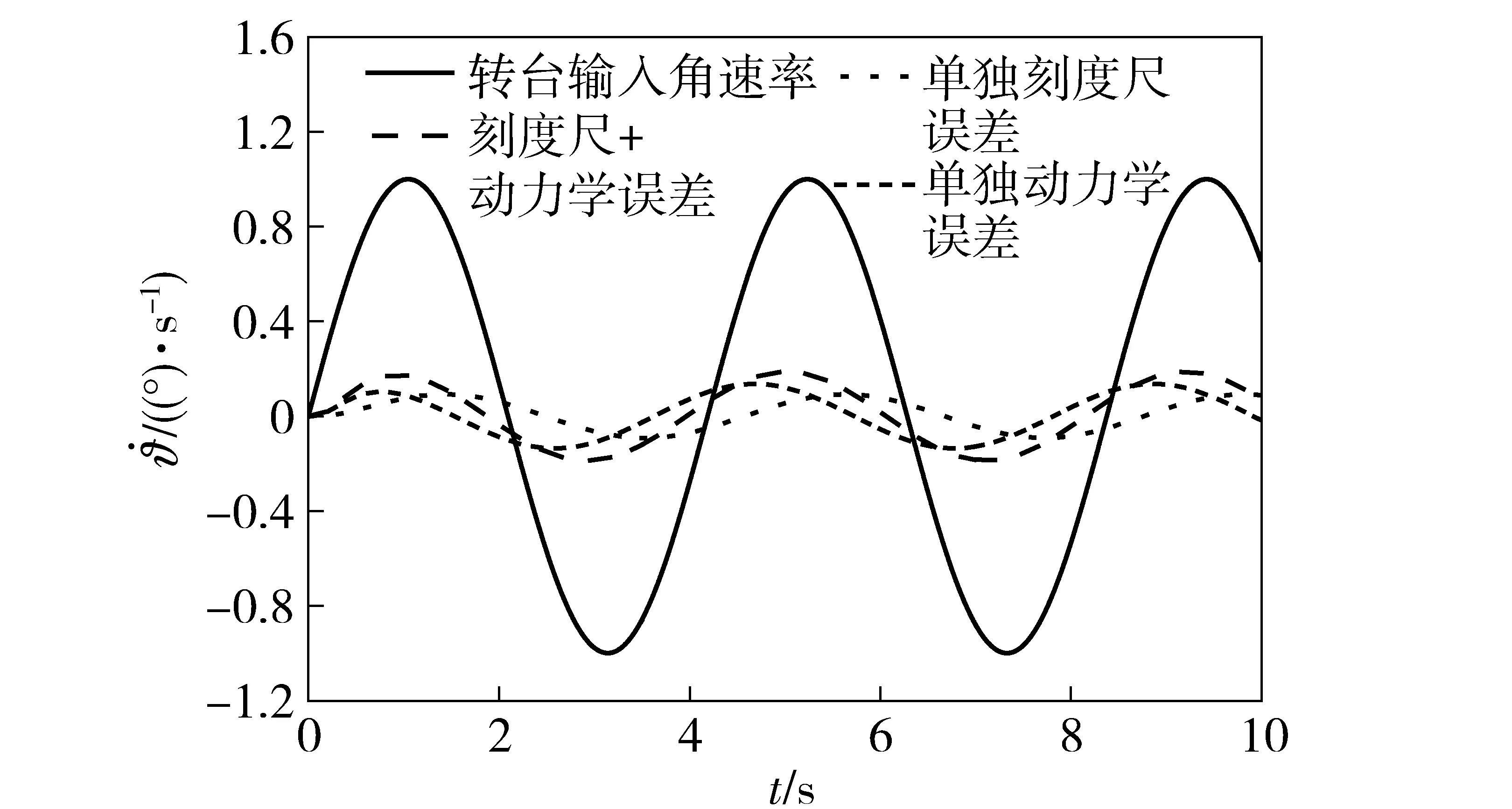
从(14)式可知：当Tgr=Ts时，不存在由动力学偏差引起的隔离度寄生回路问题；Tgr>Ts时，动力学偏差引起的隔离度寄生回路为负反馈；Tgr

进行无量纲化处理，令

(15)

(15)式代入(14)式得系统的特征方程：

(16)

图5 动力学偏差对制导回路稳定域的影响Fig.5 Effect of dynamics error on stability of parasitical loop

对(9)式变换，可得等效有效导航比Neff和等效制导时间常数Teff：

(17)

图6 动力学偏差对系统动力学的影响Fig.6 Effect of dynamics error on system’s dynamics

4 对脱靶量的影响

图7 刻度尺偏差对无量纲脱靶量的影响Fig.7 Effect of scale factor error on dimensionless miss distance

图8 动力学偏差对无量纲脱靶量的影响Fig.8 Effect dynamics error on non-dimensionless miss distance

图9 刻度尺和动力学偏差对无量纲脱靶量的影响Fig.9 Dimensionless miss distance due to scale factor and dynamics error

5 寄生回路品质测试

隔离度寄生回路品质的好坏将影响制导系统的稳定性及末制导精度，在实际生产中由于工艺偏差、环境差异及标定环境不同等因素都会造成与实际产品存在差异[8]。为了准确检验导引头隔离度寄生回路的品质，需构建半实物仿真系统，图10给出了一种捷联成像导引头隔离度寄生回路半实物开环测试系统框图。

图10 寄生回路品质半实物开环测试系统Fig.10 Semi-physical open loop test system for parasitic loop

以俯仰方向为例，5轴转台控制计算机输出sin (1.5t)的正弦信号，取典型制导参数N=3，vc/vm=1，Tα/Tg=3进行半实物仿真测试，所得结果如图11～图13所示。

图11 刻度尺偏差下阻尼品质测试结果Fig.11 Test result of damping quality due to scale factor error

图12 动力学偏差下阻尼品质测试结果Fig.12 Test result of damping quality due to dynamics error

图13 隔离度品质测试结果Fig.13 Test result of disturbance rejection rate quality

图13分别给出了只存在刻度尺、动力学偏差和两者都存在情况下，由于弹体激励扰动所产生的额外视线角速率输出。由图13中可以看出，动力学和刻度尺偏差都存在情况下导引头视线角速率输出更大，隔离度品质更差，应根据测试结果，辨识刻度尺误差或进行动力学匹配，使隔离度品质达到所要求的水平。

6 结论

针对使用捷联图像导引头，研究了角速率陀螺和探测器的刻度尺偏差和动力学偏差引起的隔离度寄生回路对系统稳定性、动态特性和脱靶量的影响，利用半实物开环测试系统对寄生回路品质进行了评价，得到以下结论：

1)陀螺刻度尺比探测器刻度尺小时，刻度尺偏差引起的隔离度寄生回路为负反馈，反之为正反馈。

2)陀螺动力学时间常数比探测器动力学时间常数大时，动力学偏差引起的隔离度寄生回路为负反馈，反之为正反馈。

3)正反馈的稳定域要远小于负反馈的稳定域，减小刻度尺和动力学偏差、减小比例导引系数N、减小导弹攻角时间常数Tα、增加制导系统时间常数Tg、减小vc/vm都有利于寄生回路的稳定。

4)隔离度寄生回路不仅使制导系统稳定性下降，而且会改变制导系统动态和稳态特性，动力学偏差仅改变动态性能，而刻度尺偏差既改变动态性能，也改变稳态性。

5)寄生回路的存在会严重影响到脱靶量，但脱靶量对负反馈寄生回路的容忍度要好于对正反馈的容忍度。

7)为了评价捷联导引头寄生回路的品质，建立了五轴半实物仿真测试模型，通过测试结果可以初步分析隔离度水平及阻尼特性。

References)

[1] 崔莹莹, 夏群利, 祁载康. 导引头稳定平台隔离度模型研究[J]. 弹箭与制导学报, 2006, 26(1):22-25. CUI Ying-ying, XIA Qun-li, QI Zai-kang. Seeker platform disturbance rejection mathematical model[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2006, 26(1): 22-25.( in Chinese)

[2] 杜运理, 夏群利, 祁载康. 导引头隔离度相位滞后对寄生回路稳定性影响[J]. 兵工学报, 2011, 32(1):28-33. DU Yun-li, XIA Qun-li, QI Zai-kang. Research on effect of seeker disturbance rejection rate with phase lag on stability of parasitical loop[J]. Acta Armamentaii, 2011, 32(1):28-33. (in Chinese)

[3] 张文渊, 夏群利, 刘大卫. 多约束制导律与导引头隔离度制导匹配性研究[J]. 兵工学报, 2015, 36(8): 1473-1480. ZHANG Wen-yuan, XIA Qun-li, LIU Da-wei. Research onguidance matching of guidance law with multiple constraints and seeker disturbance rejection rate[J]. Acta Armamenrarii, 2015, 36(8):1473-1480.(in Chinese)

[4] 温求遒, 李然, 夏群利. 全捷联成像导引头隔离度与寄生回路稳定性研究[J]. 红外与激光工程, 2014, 43(1):260-266. WEN Qiu-qiu, LI Ran, XIA Qun-li. Disturbance rejection rate and parasitical loop stability for strapdown imaging seeker[J]. Infrared and Laser Engineering, 2014, 43(1):260-266. (in Chinese)

[5] Zarchan P. Tactical and strategic missile guidance[M]. 5th ed. Virginia: American Institute of Aeronautics and Astronautics, 2007.

[6] 鄢琴涛, 李娜, 鲁天宇, 等. 导引头隔离度机理及其寄生回路频域影响分析[J]. 弹箭与制导学报, 2016, 36(2): 43-51. YAN Qin-tao, LI Na, LU Tian-yu, et al. Research on disturbance rejection rate mechanism of seeker and frequency domain analysis for parasitic loop[J]. Journal of Projectiles Rockets Missiles and Guidance, 2016, 36(2):43-51.(in Chinese)

[7] 赵超. 导引头稳定系统隔离度研究[J]. 电光与控制, 2008, 15(7):96-100. ZHAO Chao. Study on disturbance rejection rate of a seeker servo system[J]. Electronics Optics & Control, 2008, 15(7): 96-100.(in Chinese)

[8] Rudin R T. Strapdown stabilization for imagining seekers, AIAA-93-2660[R]. Reston, VA, US:AIAA 1993:1-10.

[9] William N F, Paul Z. Radome induced miss distance in aerodynamically controlled homing missile[C]∥17th Fluid Dynamics, Plasma Dynamics, and Lasers Conference. Snowmass,CO, US:AIAA,1984.

[10] Garnell P, East D J. Guidance weapon control systems[M]. Oxford,UK: Pergamon Press, 1977.

[11] 宋韬, 林德福, 祁载康. 平台导引头隔离度模型辨析[J]. 北京理工大学学报, 2013, 33(6):575-580. SONG Tao, LIN De-fu, QI Zai-kang. Analysis on the model of seeker disturbance rejection rate[J]. Transactions of Beijing Institute of Technology, 2013, 33(6):575-580. (in Chinese)

[12] 李富贵, 夏群利, 蔡春涛, 等. 导引头隔离度寄生回路稳定性及测试方法[J]. 北京理工大学学报, 2014, 33(8):801-805. LI Fu-gui, XIA Qun-li, CAI Chun-tao, et al. Stability and measurement of seeker disturbance rejection rate parasitic loop[J]. Transactions of Beijing Institute of Technology, 2014, 33(8):801-805. (in Chinese)

[13] 朱华征, 范大鹏, 马东玺, 等. 导引头伺服系统隔离度与测试[J]. 光学精密工程, 2009, 17(8):244-249. ZHU Hua-zheng, FAN Da-peng, MA Dong-xi, et al. Disturbance isolation index of seeker servo system and its test[J]. Optics and Precision Engineering, 2009, 17(8): 244-249.(in Chinese)

[14] 鄢琴涛, 夏群利, 祁载康, 等. 全捷联导引头隔离度指标工程计算方法[J]. 红外与激光工程, 2015, 44(12): 3788-3793. YAN Qin-tao, XIA Qun-li, QI Zai-kang, et al. Engineering calculation method of strap-down seeker disturbance rejection rate index[J]. Infrared and Laser Engineering, 2015, 44(12): 3788-3793. (in Chinese)

[15] 李富贵，夏群利，祁载康，等. 全捷联导引头寄生回路影响与辨识校正[J]. 系统工程与电子技术, 2013, 35(8):1717-1722. LI Fu-gui, XIA Qun-li, QI Zai-kang, et al. Effect of parasitical loop on strap-down seeker and compensated with identification method.[J]. Systems Engineering and Electronics, 2013, 35(8): 1717-1722. (in Chinese)

Test of Parasitic Loop Quality of Strapdown Seeker

BAI Rui1, XIA Qun-li1, DU Xiao1, LU Tian-yu1,2

(1.School of Aerospance Engineering, Beijing Institute of Technology, Beijing 100081, China; 2.School of Mechatronical Engineering, Beijing Institute of Technology, Beijing 100081, China)

In order to analyze the effect of disturbance rejection rate parasitic loop on strapdown imaging seeker, a model of disturbance rejection rate parasitic loop of strap-down seeker is established. Nondimensionalized method is used to obtain dimensionless characteristic equation, the effects of the guidance parameter and the scale factors and dynamic errors of gyro and seeker on the stability region of parasitical loop as well as the effect of parasitic loop on the dynamics of guidance system are studied by using Routh criteria, and the nonlinear models are established. Monte Carlo method is used to study the change of miss distance with scale factor and dynamics errors. A semi-physical open loop test system is established to appraise the quality of disturbance rejection rate parasitic loop. The research result shows that the scale error and the mismatch between the rate gyro and the detector are the main factors that cause the DRE parasitic loop. The numerical value of the error and mismatch decides whether the parasitic loop is positive or negative feedback. The stable domain of positive feedback is far less than that of negative feedback, while the miss distance is more sensitive to guidance system deviation. To improve the guidance precision, five axis turntable semi-physical simulation test system was used to test and calibrate the damping characteristics of parasitic loop, by which the parasitic effect can be eliminated by eliminating the scale error and the mismatch, or at least be reduced by constructing a negative feedback parasitic loop.

ordnance science and technology; strapdown seeker; parasitic loop; scale factor error; dynamics error; semi-physical test

2016-06-27

航空科学基金项目(20150172001)

白瑞(1988—)，男，博士研究生。E-mail:bairui19880403@163.com

夏群利(1971—)，男，教授，博士生导师。E-mail:1010@bit.edu.cn

TJ765.3+31

A

1000-1093(2017)03-0494-07

10.3969/j.issn.1000-1093.2017.03.011