栅格水沙耦合模型在水保试验区土壤侵蚀时空模拟中的应用研究

2017-04-10陈发先

水利规划与设计 2017年2期

关键词：水沙水保土壤侵蚀

陈发先

（辽宁省水土保持局，辽宁沈阳 110003）

栅格水沙耦合模型在水保试验区土壤侵蚀时空模拟中的应用研究

陈发先

（辽宁省水土保持局，辽宁沈阳 110003）

本文采用水沙耦合模型，以栅格（1km×1km）为计算单元，对辽宁某水保试验区进行土壤侵蚀模数时空模拟，并结合试验区实测水量和土壤侵蚀数据对模型精度进行评价，同时还对区域不同水土保持措施下的土壤侵蚀模数进行了评价。研究结果表明：栅格水沙耦合模型可用于区域土壤侵蚀模数的空间模拟，模拟水量和土壤侵蚀模数与实测值误差小于25%；坡度为15°的水保工程措施可明显减少区域土壤侵蚀模数，相比于其他措施区域土壤侵蚀量削减35.5%～98.4%。研究成果对于不同水保措施下的水保时空效果模拟提供模拟方法参考。

水沙耦合模型；栅格计算单元；土壤侵蚀时空模拟

区域水土流失保护规划重在对区域土壤侵蚀空间分布进行准确评估，而在水保试验区，不同水土保持措施下的区域土壤侵蚀量不同，为此需要对区域土壤侵蚀进行空间分布的模拟分析。有许多学者对区域的土壤侵蚀进行计算，并取得一定的研究成果［1-5］，但是不同水土保持措施下对区域土壤侵蚀的影响各异，需要结合不同水保措施下区域的下垫面数据对区域土壤侵蚀模数空间分布进行整体分析。MULSE土壤侵蚀模型将水量作为模型输入，进行区域土壤侵蚀模拟，为水沙模型耦合提供途径，并在一些区域土壤侵蚀模拟得到具体应用［6-10］。但是在水保试验区土壤侵蚀时空模拟还未进行相关应用，特别是在辽宁地区，为此本文将产流模型与MULSE模型进行耦合，并加入坡面汇沙方程，并以栅格（1km×1km）为计算单元，实现区域水保试验区土壤侵蚀时空分布全过程模拟。

1 栅格水土流失模型原理

本文将产流模型与MULSE模型进行耦合，并加入坡面汇沙方程，并以栅格（1km×1km）为计算单元，实现区域水保试验区土壤侵蚀时空分布全过程模拟。耦合模型产流模型计算原理为：

假设水保区域不透水的面积比例参数IM=0，则区域产流面积方程为：

在方程（1）中f表示为栅格产水面积，km2；F表示为栅格的面积，km2；W′表示为栅格产流单点蓄水量，mm；WMM表示为W′的最大值，mm；B表示为区域蓄水容量分布曲线指数。

软件部分主要包括光纤连接信息采集、智能光纤托盘与单元控制器的485数据传输、485数据到蓝牙数据的转换以及手机端APP设计等。本文重点对光纤连接信息采集进行介绍。

基于栅格水沙耦合模型，以栅格（1km×1km）为计算单元，计算不同水保工程措施（见表3）下的土壤侵蚀空间分布，见图4。

由（1）式积分可得：

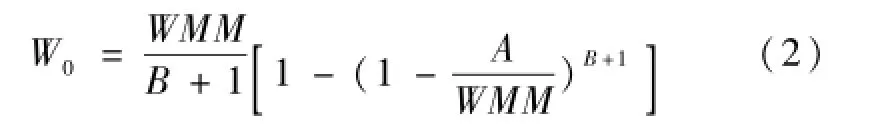
与W0值相应的纵坐标值A为：

作为整个线损管理平台的基础构成，数据库管理模块的应用，主要作用于向其他功能模块传送信息、资料、数据，或是储存、备份、整理、分类由其他功能模块所收集到的数据信息，再者就是将一些技术性数据传送至高级应用软件中。因此，在实际的构建数据库管理系统时，不仅需要保证其拥有海量的内容空间、共享功能，同时也应带有一定的开放性、安全性，一般可采用基于NT环境的SQLServer大型数据库。

表1和表2为栅格水沙耦合模型在水量和土壤侵蚀量的精度评价结果，从各试验场次评价结果可以看出，栅格水沙耦合模型在区域的土壤侵蚀模拟具有较好的精度，计算的水量和土壤侵蚀量和实测水量和土壤侵蚀量之间的误差值均小于25%，栅格水沙耦合模型在水保试验区的土壤侵蚀量和水量具有较好的适用性。图2和图3为水量过程和土壤侵蚀量过程评价结果，从图中可以看出栅格水沙耦合模型计算值和观测值相关性较好。

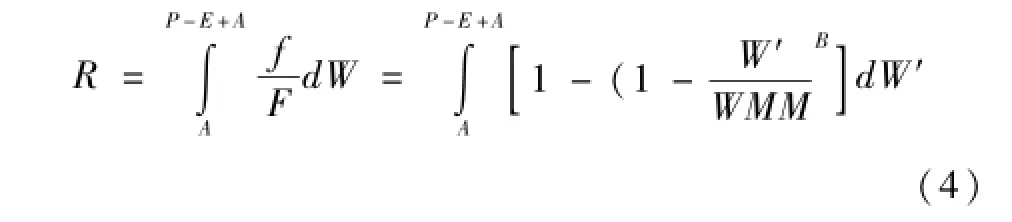
其中在方程（4）中如果P-E+A＜WMM，则：

对于应用型院校的教师来说，牢固掌握专业基础知识是能够进行教学工作的基本条件，也是作为一名专业教师的基本素质。一般来说，专业基础知识是在教师正式步入教学岗位之前，在校学习阶段就应具备的能力。按我国的人才培养模式和对教师岗位的要求，应用型本科院校一般要求教师具备博士学历，所以绝大多数教师都具备过硬的专业基础知识。同时，对于应用型本科院校，院校管理者对教师做出聘任、考核、奖励、提升时，也都会对教师的专业知识进行考察。因此，绝大部分应用型高校教师均具备与其教学任务相匹配的专业基础知识。

若P-E+A≥WMM，则：

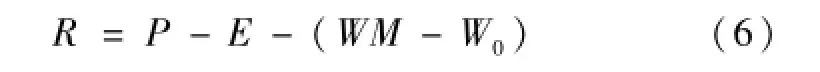
其中在方程（6）中 W0表示为栅格计算单元土壤蓄水量初值，mm；WM表示为水保试验区蓄水容量平均值，mm；R表示为总的产水量，mm。

新经济背景下，社会对物流的要求已越来越高，这必然要求对我国快递业物流市场4Ps营销组合策略进行优化。新经济背景下，快递业物流市场营销组合策略优化的方案是：以战术4Ps营销组合策略为基础，将4Cs、4Rs融入战术4Ps中，形成新经济背景下新的4Ps营销组合策略[1]。

泥沙蓄泄方程：

在上述方程中，WS表示的是泥沙蓄量，IS表示的是坡面时段的产沙速率，S表示的是坡面时段出沙速率，KS表示的是坡面汇沙的时间。

将公式（7）进行差分并代入（8）式，可得到坡面的汇沙公式：

对高速公路进行标准化的设置是一项较为复杂的系统性工程，因此在实施的过程中需要对各项内容进行具体的标准设定。

2.3 水保试验区土壤侵蚀空间模拟成果

其中CSS为坡面汇沙系数，其计算公式为：

2 模型应用

2.1 水保试验区概况

本文以辽宁西部某水保试验区为研究区域，该区域主要的土壤质地为壤土和粘土，区域主要的土地利用方式为林地、草地以及耕地，区域坡度集中在15～30°。为观测不同水保工程下对区域土壤侵蚀量的影响，区域内设置了降水量、水量以及土壤侵蚀观测仪器，对区域降水量、水量以及土壤侵蚀量进行观测，各观测点位置见图1。

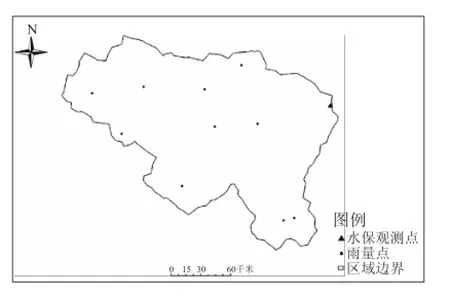
图1 水保试验区观测点位置图

2.2 模型精度评价及适用性分析

结合水保试验区域观测的多场次降水量、水量以及区域土壤侵蚀量数据，对栅格水沙耦合模型土壤侵蚀模拟的精度进行分析并对模型的适用性进行评价，由于模型为水沙耦合模型，需要对模型计算的水量和土壤侵蚀量均进行评价和分析，模型计算水量和沙量的评价精度结果见表1和表2。并选取两个场次进行了水量和沙量的过程比较图，结果见图2和图3。

在进行完产流模型进行后，以栅格产水量作为MULSE模型的水量输入，考虑文章篇幅，MULSE模型计算原理可详见参考文献［10］，本文在栅格产水产沙模型耦合的基础上，加入区域坡面汇沙方程，流域坡面汇沙泥沙平衡方程：

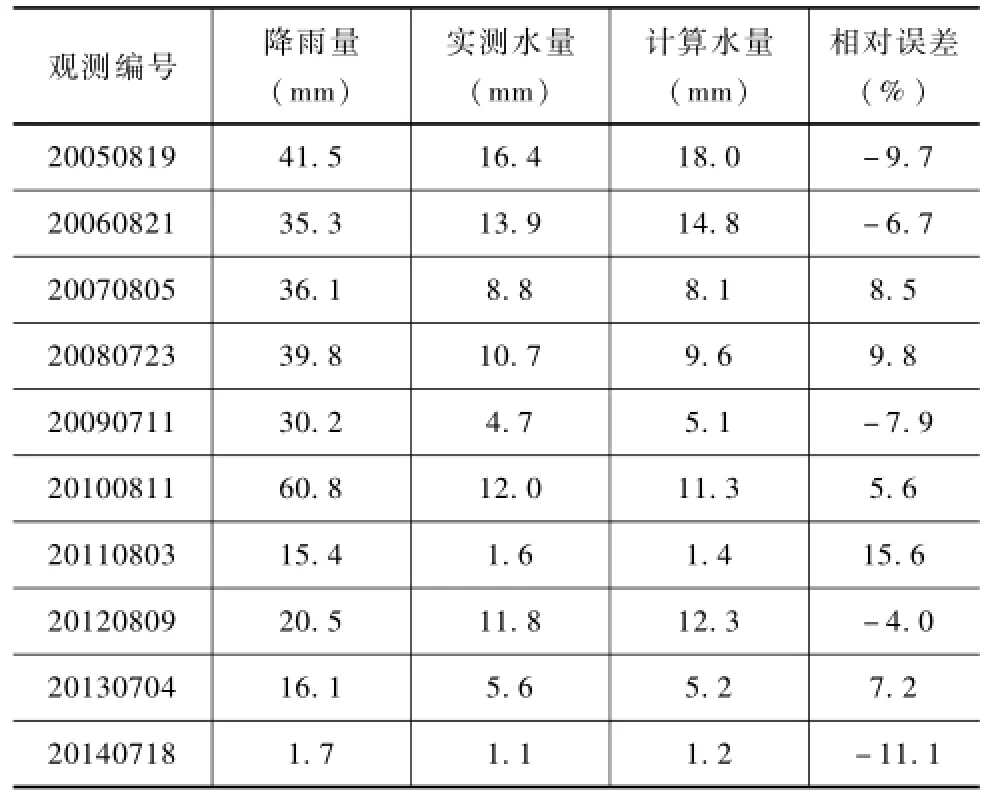
表1 栅格水量精度评价

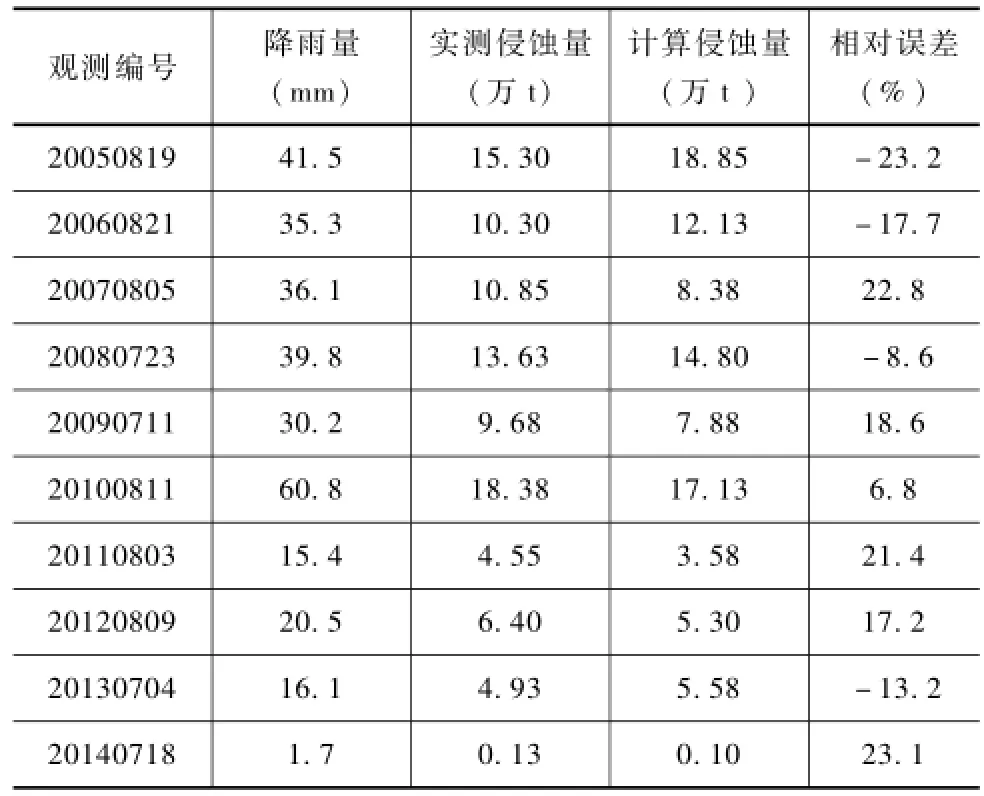
表2 栅格土壤侵蚀量精度评价

则栅格总的产水量R值的计算方程为：

将13个设计矩阵Aij(k)累加，即得各项指标的优先得分矩阵：再对得分矩阵Aij关于j，即按行累加：再求出Aij按行累加后的最大值、最小值，令∑Amax=max{∑A1，∑A2，…，∑A6}，∑Amin=min{∑A1，∑A2，…，∑A6}，则与∑Amax相对应的因子同其它因子相比重要程度最高，而与∑Amin相对应的因子的重要程度最低。取amax=1，amin=0.1，记

乳酸脱氢酶是一种糖酵解酶，在缺氧条件下能够将丙酮酸转化成乳酸，当机体受到外界某种应激，乳酸脱氢酶活力会升高[22]。如图4所示，保活5、7、9和11 h后血清中乳酸脱氢酶含量都显著高于未处理前的值（p＜0.05），分别上升 30.53%、32.33%、37.38%和58.40%，保活时间达到11 h时，乳酸脱氢酶含量骤增。清水中复苏24 h后，保活5、7、9 h基本恢复麻醉前的水平。这与聂小宝等[19]人研究的低温无水状态下LDH的变化趋势一致。

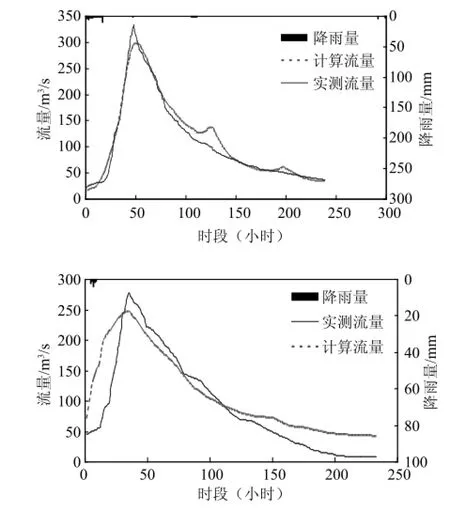
图2 水量过程评价图

图3 土壤侵蚀量过程评价图

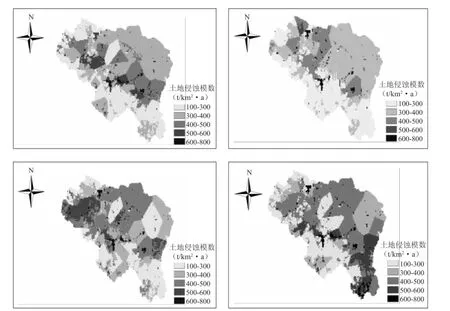
图4 不同水保措施下区域土壤侵蚀空间分布图

对方程（1）进行积分求解得到方程：

思维地图是David Hyerle博士在1988年设计的一种帮助学习的视觉语言工具。思维地图包含多种图示类型，分别是圆圈图、气泡图、双气泡图、树形图、括号图、流程图、复流程图和桥型图。不同类型的思维地图有其适用范围，其中圆圈图适用于头脑风暴；气泡图适用于对事物进行描述；双气泡图适用于事物或知识点间的比较；树形图适用于对事物进行分组或分类；括号图适用于分析事物整体与部分的关系；流程图适用于列举顺序、过程、步骤等；复流程图适用于展示和分析因果关系；树形图适用于进行类比推理。

表3为不同水保工程措施，基于栅格水沙耦合模型对不同水保工程措施下区域的土壤侵蚀进行空间分布模拟分析。图4为不同水保工程措施下区域土壤侵蚀模数空间分布图，从图中可以看出区域土壤侵蚀空间分布较为不均匀，这主要和区域降水、下垫面以及水保措施有关。1#和2#水保工程措施下的土壤侵蚀模数总体分布上小于 3#和4#水保工程措施下的土壤侵蚀模数。

表3 不同水保措施方案

2.4 不同水保工程措施下的土壤侵蚀量对比

为定量对不同水保工程措施下的土壤侵蚀量进行分析，结合栅格水沙耦合模型对不同水保工程措施下区域总的土壤侵蚀量进行计算，并进行对比分析，计算结果见表4。

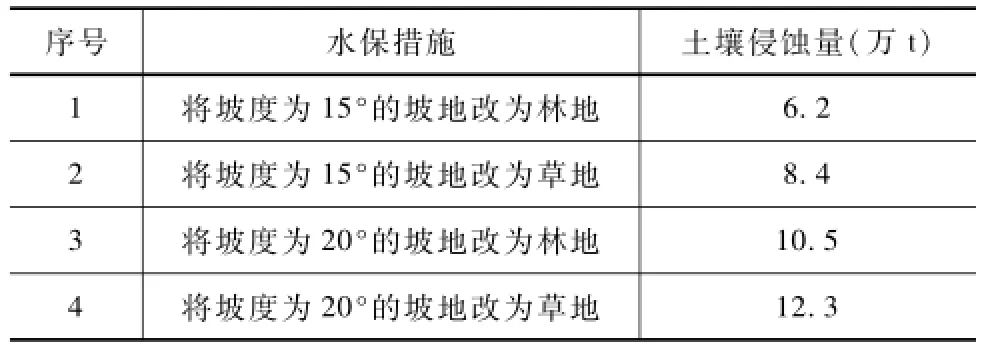
表4 不同水保工程措施下试验区土壤浸蚀量对比

从表4可以看出，1#水保工程措施下其土壤侵蚀量最小，为6.2万t，而在4#水保工程措施下其土壤侵蚀量最大，为12.3万t，说明将坡度为20°的坡地改为草地，不利于区域土壤侵蚀量的减少，而将坡度为15°的坡地改为林地，将使得区域土壤侵蚀量明显减少，相比于其他水保工程措施，水保试验区在 1#水保工程措施下其土壤侵蚀量减少35.5%～98.4%，土壤侵蚀量削减程度明显。