基于APSO-BP算法的水库生态优化调度研究

2017-04-10胡晓松

水利技术监督 2017年1期

关键词：需水水库粒子

胡晓松

（辽宁省鞍山水文局，辽宁鞍山114000）

基于APSO-BP算法的水库生态优化调度研究

胡晓松

（辽宁省鞍山水文局，辽宁鞍山114000）

APSO-BP算法可实现粒子群优化的自动调整，解决传统粒子群优化算法收敛性较差，局部易出现极小值的局限，文章引入APSO-BP算法对辽宁某水库生态调度进行优化计算。研究结果表明：APSO-BP算法的收敛精度和全局优化搜索能力都好于传统粒子群优化算法，经APSO-BP算法优化下的水库生态调度可以满足流域的生态蓄水，流域最小生态需水满足度达到75%，适宜生态需水满足度达到66.7%，生态优化调度结果明显好于传统粒子群优化算法。APSO-BP算法可用于水库生态优化调度。研究成果对于水库生态调度方案以及区域生态蓄水规划配置提供方法参考。

APSO-BP算法；传统粒子群算法；水库生态优化调度；生态满足度

当前，但随着流域生态保护建设进一步得到关注，水库的生态调度也成为水库运行调度的主要目标之一，对于水库优化调度，国内外学者研究较多，研究的方法也较为成熟［1-6］。近年来，许多算法在水库生态优化调度中得到应用，在这些方法中，粒子群优化算法运用较为广泛，该算法可实现水库的多个目标优化，但传统粒子群优化算法在计算过程中存在收敛精度不高，局部易出现极小值的局限。近期，APSO-BP算法引入粒子自动适应函数对计算粒子进行调整计算，能解决传统粒子群算法局部出现极小值以及收敛不高的局限，在水资源优化领域得到具体应用［7-11］，本文引入APSO-BP算法，以辽宁某水库为研究实例，对水库生态调度进行优化计算，并分析APSO-BP算法在水库生态调度的适用性。

1 APSO-BP算法原理

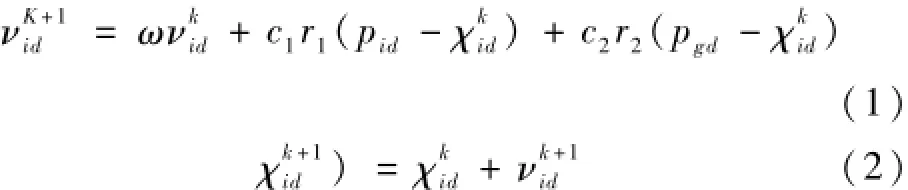
该算法假设在N维空间里面有M个粒子，每个计算粒子赋予计算位置属性Yj，根据每个粒子计算的位置属性值代入目标函数求解得到不同计算粒子的目标函数适应值，对每个粒子进行目标优化搜索求解，得到每个位置的最优位置，粒子自适应算法POS的计算公式为：式中，ω表示为模型计算的速度的惯性权重系数；K表示为模型迭代计算的次数；i表示计算的粒子的个数；d表示为计算的空间维数，在本文模型计算的空间维数位2维C1和C2分布表示为模型训练计算的学习因子的个数，本文中2个学习因子数r1和r2分别表示［0-1］之间的随机数，其中νid∈［-νidmax，νidmax］，在模型计算中，惯性权重系数ω对模型计算影响较大，本文引入动态自动适应的权重系数调整算法对模型粒子计算速度的惯性权重系数进行计算，ω模型计算的公式为：

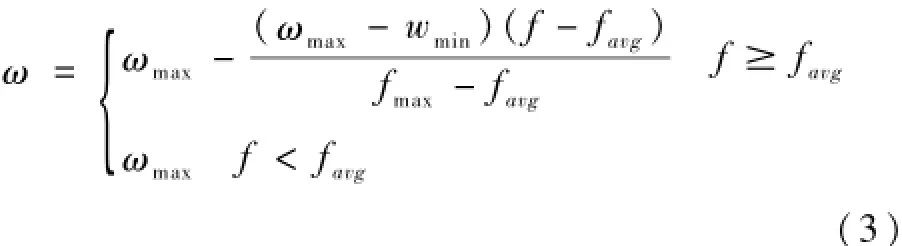
式中，ωmax和wmin分别表示为粒子速度最大的惯性和最小惯性权重系数；f表示为模型计算的粒子自动适应目标函数的值；favg表示为模型计算的自动适应粒子属性值的平均值；fmax表示为模型计算粒子自动适应目标函数属性的最大值。

在计算粒子自动适应目标函数值的基础上，采用APSO算法对Bp网络单元进行优化求解，优化求解目标为使得模型计算的均方程值最小，计算方程为：

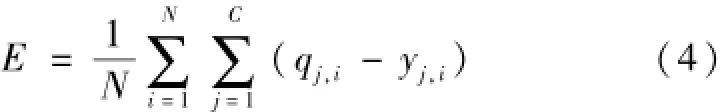
式中，N表示为模型训练计算样本的个数；qj，i表示为第i个计算粒子在模型节点的属性位置值；yj，i则表示为第j个训练样本在第i个计算节点的属性位置值；C则表示为模型输出的神经网络单元的个数。

APSO算法对模型网络计算进行优化求解，并对每个粒子的位置属性χ和速度ν属性进行更新计算，对每个粒子更新计算的方程为：

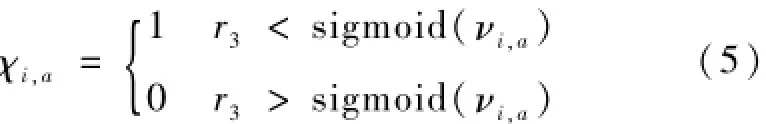
式中，r3表示为模型计算的随机数。

在APSO-BP算法中对所有隐含的粒子数采用算法进行目标约束求解，约束方程为：

式中，Z表示为模型隐含单元的个数；a和c分别表示输入计算单元层的个数；a表示为1-10之间的整数。

此外本文采用Schaffer函数对模型的收敛度以及优化搜索能力进行求解，求解的函数为：

式中，x表示为模型计算的收敛度；y表示为模型计算的优化搜素能力，一般来说x和y小于4。

2 实例应用

2.1 水库概况

水库1962年建成。控制面积2376km2，总库容9.71亿m3，水库主要以防洪为目标，兼顾供水。为保护下游沙漠生态，水库开始进行生态调度，应用APSO-BP算法对水库生态调度进行优化，并结合水库的防洪与供水目标进行优化调度。

2.2 区域生态需水计算

基于水库下游水文站2000～2015年流量数据，采用最小生态径流方法［12］和适宜生态径流方法［13］对河道逐月最小和适宜生态径流进行计算，计算结果见表1。

从表1中可以看出，区域最小生态需水在枯水期由于来水量较少，一般在15m3/s以下，进入丰水期，流域的最小生态需水量增加到15m3/s以上。河道最小生态需水量是保证河流生态系统基本平衡所需要的水量，但是不能对流域水生态有所改善和保护，而流域适宜生态需水量可以维持流域水生态系统的健康，并对区域水生态系统进行一定的程度的改善。从表1中可以看出，区域的适宜生态需水都大于区域最小生态需水，且存在丰水期、枯水期的差异。因此在水库生态调度过程中，需要对丰水期和枯水期的水量进行优化分配，在满足水库防洪和供水目标的同时，需要满足水库下游河道的生态需水量的目标，对于不同算法水库生态调度结果按照对下游适宜生态需水和最小生态需水满足度来分析水库生态优化优化调度的结果。

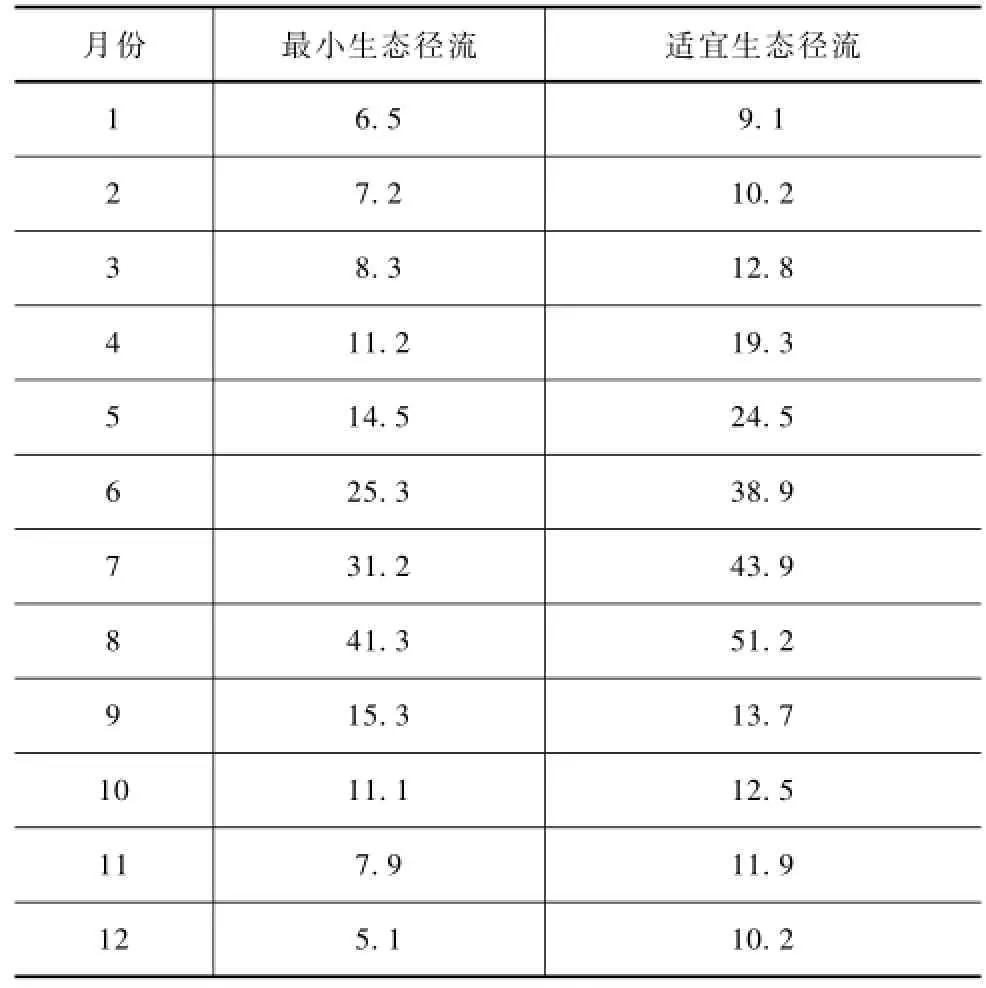
表1 逐月生态径流计算结果

2.3 不同算法收敛度和全局搜索能力分析

采用Schaffer方法对APSO-BP算法和传统粒子群优化算法收敛精度和全局搜索能力进行测试，结合10组随机数据分析两者方法的收敛精度和全局搜索能力，计算结果见表2。

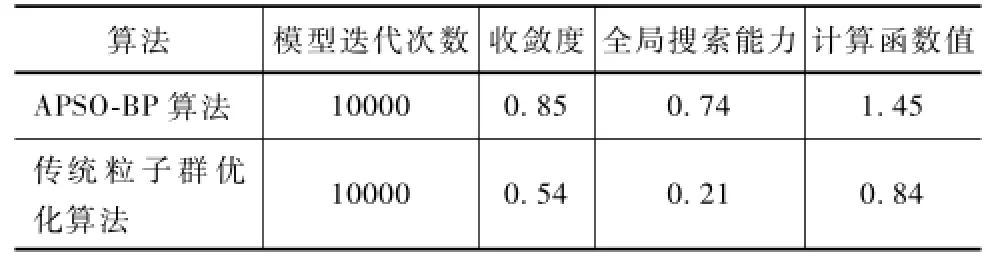
表2 Schaffer方法下模型的测试结果

从表2中可以看出，经过Schaffer方法测试后，APSO-BP算法的收敛度和全局搜索能力都要明显好于传统粒子群优化算法，APSO-BP算法的Schaffe函数计算值为1.45，而传统粒子群优化算法的Schaffe函数计算值为0.84，从测试结果说明APSO-BP算法因为采用粒子自动适宜调整函数对粒子的优化位置进行调整计算，收敛度和全局搜索能力好于传统粒子群优化算法。

表3 水库生态优化调度结果

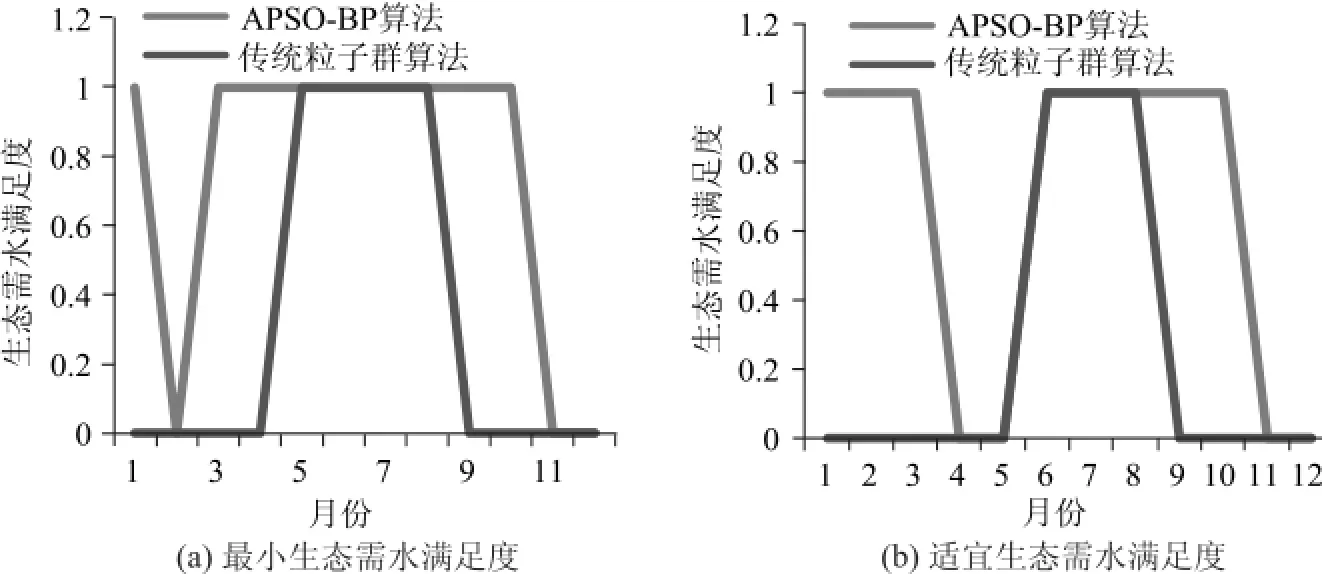
图1 不同优化算法下水库生态调度流域生态需水满足度分析

2.4 基于APSO-BP算法的水库生态调度结果分析

结合APSO-BP算法和传统粒子群算法分别对水库进行逐月生态优化调度，分析经过生态优化调度后下游河道生态需水满足度，分析结果见表3和图1。

表3为APSO-BP算法和传统粒子群算法的水库生态优化调度结果，从调度结果可以看出，APSO-BP算法下水库生态调度水量对于区域最小生态需水满足度达到75%，而传统粒子群优化算法下的水库生态调度水量对于区域最小生态需水满足度仅为33.3%，明显低于APSO-BP算法下水库生态调度后区域最小生态需水满足度，从各月份最小生态需水满足度中可以发现在枯水期水库由于来水量的减少，区域最小生态需水满足度较低，进入丰水期后，由于水库来水量增加，区域的最小生态需水满足度较高。APSO-BP算法下水库生态调度后区域适宜生态需水满足可以达到66.7%，而传统粒子群优化算法下的区域适宜生态需水满足度仅为25.0%，可见对于区域水生态保护较为重要的适宜生态需水量，APSO-BP算法优化后的水库生态调度满足度也明显高于传统粒子群优化算法，总体上看，APSO-BP算法下区域的最小生态需水满足度要好于适宜生态需水的满足度。