基于改进的IDW模型的区域蒸散发空间插值技术研究

2017-04-10林树刚

水利技术监督 2017年1期

关键词：蒸发皿变差插值

林树刚

（辽宁省沈阳水文局，辽宁沈阳110500）

基于改进的IDW模型的区域蒸散发空间插值技术研究

林树刚

（辽宁省沈阳水文局，辽宁沈阳110500）

文章引入改进的IDW模型，将改进的IDW模型用于辽宁中部区域蒸散发空间插值研究中，解决无资料地区蒸散发资料插值移用的问题，并结合区域实测蒸发皿蒸发数据对比分析改进前后的IDW模型在区域蒸散发的插值精度。研究结果表明：改进的IDW模型由于引入变差函数对距离权重进行修正，在蒸散发插值精度上好于传统的IDW模型，插值计算的年尺度蒸散发和实测蒸散发的提高0.31，绝对误差均值缩减101.6mm；在月尺度上，插值精度低于年尺度，绝对误差缩减7.8mm；区域蒸散发空间分布总体上受高程影响较大。研究成果对于区域蒸散发插值技术提供参考价值。

改进的IDW模型；变差函数；蒸散发空间插值；辽宁中部区域

当前，随着中小河流治理工程措施的逐步实施，在工程措施实施之前，需要对中小河流整治工程进行设计，而治理设计涉及到河流水文计算，中小河流水文计算往往处于无资料地区，需要移用或者内插得到区域的水文数据，而区域蒸散发是水文循环的重要因素，对于无资料地区水文计算而言，区域蒸散发主要通过附近蒸发站进行移用，另外一种方法则是采用空间插值的方法进行插值得到，第一种方法需要附近有蒸发站点才可以进行移用，且有区域面积的限制，而空间插值方法则可以在整个空间上进行内插，不受站点和区域面积的限制，在流域降水和蒸散发插值中得到具体应用，并取得一定的成果［1-6］。在这些方法中，传统IDW模型由于可以将多个已知点进行插值，在流域水文要素的空间插值中，运用较为广泛［7-11］。但是传统IDW模型不能考虑各个已知点对插值点的权重影响，存在一定精度局限，有学者对传统的IDW模型进行改进，引入变差函数计算不同已知点的权重，提高要素空间插值的精度，改进的IDW模型在水资源领域运用还较少，为此本文引入改进的IDW模型。以辽宁中部区域为研究实例，对研究区的蒸散发进行空间插值计算，并结合实测蒸发站对比分析改进前后的IDW模型对区域蒸散发空间插值精度的影响，研究成果对于无资料地区水文要素插值技术提供参考价值。

1 改进的IDW模型原理

IDW模型即为反距离加权平均方法，其主要表达式为：

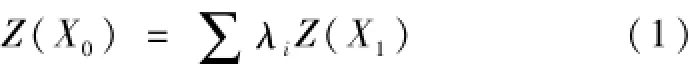
其中λ的计算公式为：

式中，Z（X0）表示为蒸发皿观测点值；Z（X1）表示为蒸发空间插值；L0表示为第i个蒸发点距离需要插值的点之间的距离；P表示为插值前需要估计的模型参数；λi为已知点的权重值。

在IDW模型的基础上加入变差函数，对传统IDW模型的权重λi进行改进，其改进后的表达式为：

式中，D0表示为变差函数在已知点和插值点的参数的取值。虽然方程（3）加入变差函数使得权重定值更为简单，但是方程（3）和方程（2）不能通过P值来调整对应的权重，为此对两个方程进行调整，调整后的表达式为：

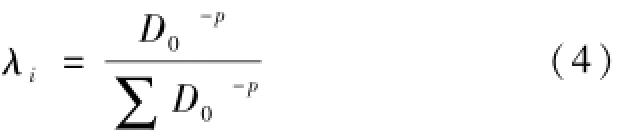
在进行权重计算时，首先需要计算D0值，D0值的计算表达式为：

式中，g和γ表示为L距离对应的模型插值拟合参数。为消除观测值在插值计算时的延迟影响，将方程（5）进行演变，演变后的方程表达式为：

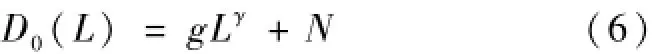
式中，N表示为观测值两点之间的标准差，其中N的计算表达式为：

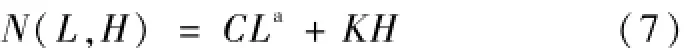
式中，L和H分别表示为两点之间的距离以及高程差。C以及K和a则表示为模型的计算参数。

经过变差系数和标准差计算后，IDW模型的权重值可以进一步改进为：

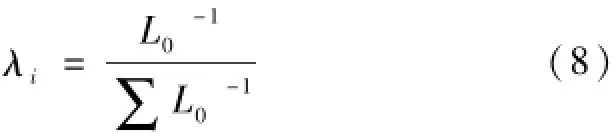
引入变差函数和观测值两点之间的标准值对改进的IDW模型进行耦合，耦合后的方程表达式为：

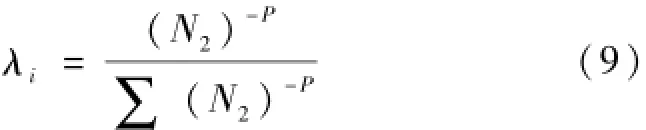
式中，N表示两点观测值之间的标准差；P表示为改进的IDW模型的计算参数。

2 实例应用

本文以辽宁中部某区域为研究区域，研究区集水面积265.5km2，流域多年平均降水量为519.6mm，多年平均蒸发量为350mm，此外考虑到IDW模型需要插值点和已知点之间的距离，收集了区域内分辨率为90s的区域数字高程数据，见图1。

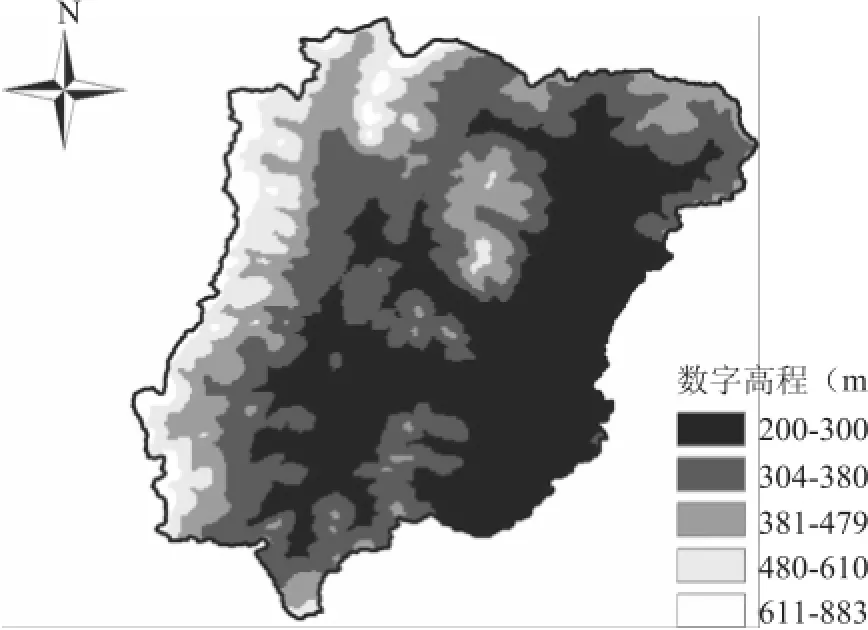
图1 研究区域DEM S数字高程图

2.1 年尺度区域蒸散发插值精度对比

分别结合改进的IDW模型和传统IDW模型对区域的年尺度蒸散发能力进行空间插值，并集合研究区域实测的蒸散发皿蒸发对比两种模型在年尺度插值精度的影响，研究结果见表1、图2和图3。

表1 改进前后的IDW模型内插蒸发与实测蒸发皿蒸发精度对比分析

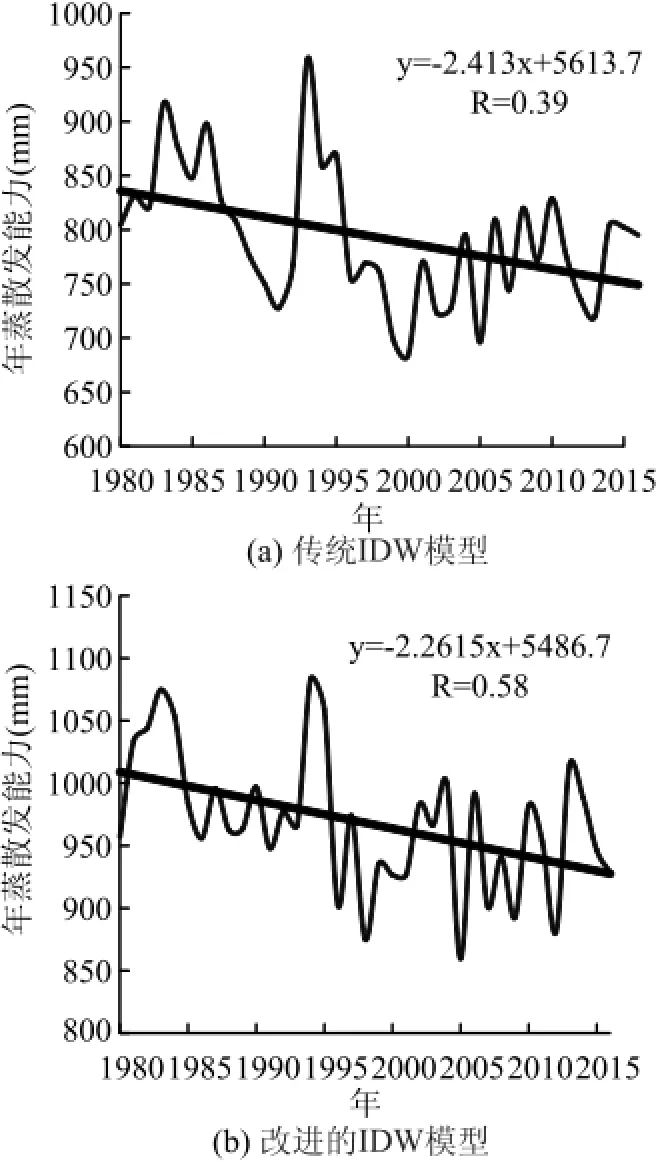
图2 不同模型内插蒸发计算过程图

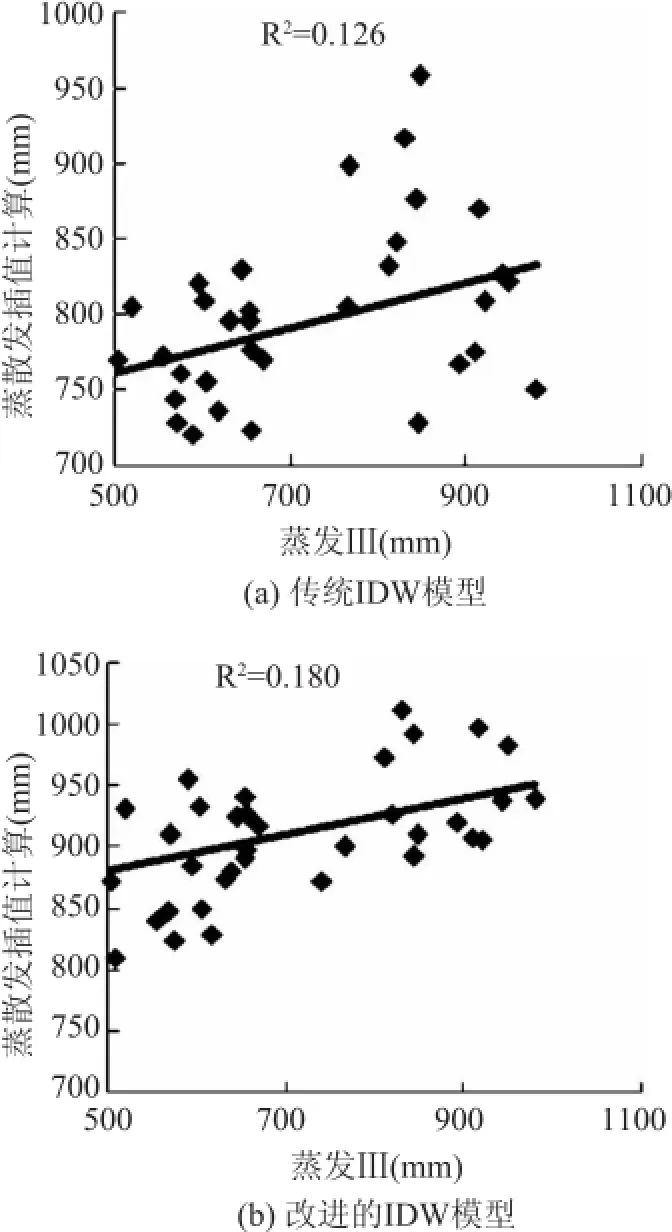
图3 不同模型内插蒸发计算与实测值相关图

表1为改进的IDW模型和传统的IDW对区域蒸散发能力空间插值结果的对比，从结果中看出，改进的IDW模型和实测蒸发皿蒸散发之间的绝对误差在5.82～112.11mm之间，绝对误差的平均值为43.8mm，传统的IDW模型蒸散发空间插值计算值和实测的蒸发皿蒸散发之间的绝对误差在53.64～281.02mm之间，绝对误差的平均值为145.4mm，在插值计算值和实测的蒸发皿蒸散发绝对误差上，改进的IDW模型比传统的IDW模型减少101.6mm，相比于传统IDW模型，改进的IDW模型在插值精度上得到明显提高。

图2为两种模型的年蒸散发过程，从图上可以看出改进的IDW插值计算的蒸散发过程线性相关趋势要好于传统的IDW模型。为更好的分析改进的IDW模型和传统IDW模型的蒸散发空间插值精度。图3为两种模型空间蒸散发插值与实测蒸发皿蒸散发之间的相关图，从图中可以看出，改进的IDW模型的相关系数达到0.79，明显高于传统的IDW模型的相关系数的0.48。

2.2 月尺度区域蒸散发插值精度对比

在年尺度蒸散发插值精度对比的基础上，结合改进的IDW模型和传统IDW模型对月尺度蒸散发进行月尺度的空间插值技术，并结合研究区域实测的蒸散发皿蒸发对比两种模型在年尺度插值精度的影响，研究结果见表2和图4。

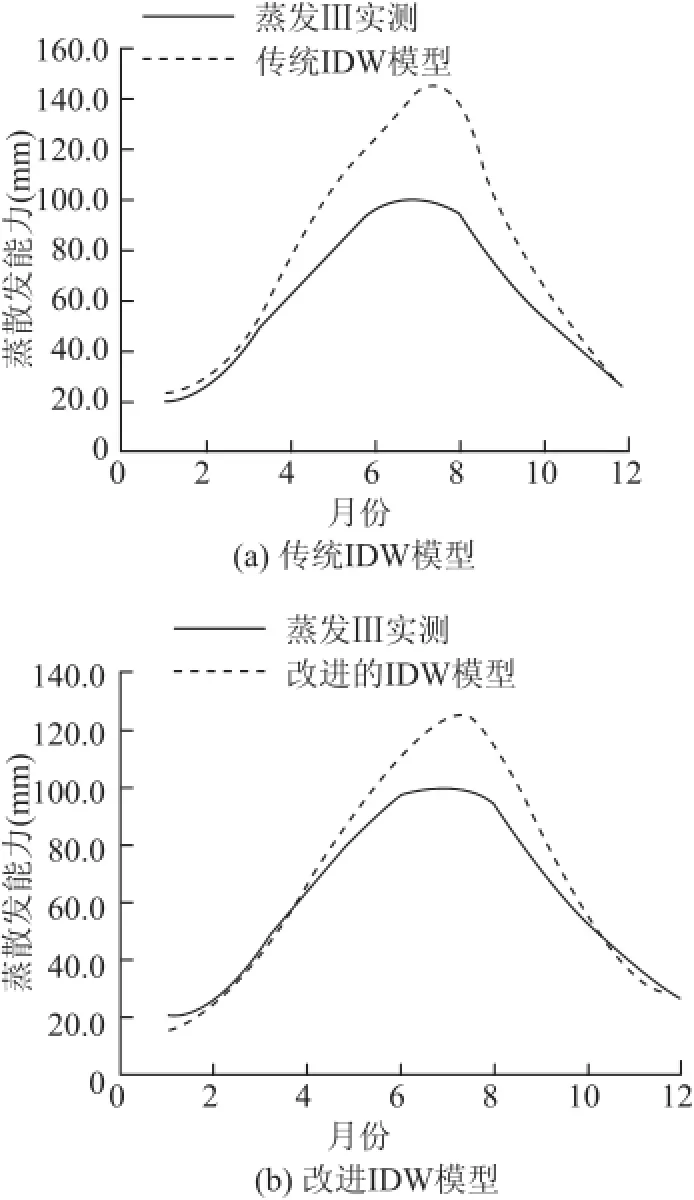
图4 不同模型月尺度蒸发插值计算结果与实测蒸发皿蒸发过程对比图

表2为不同模型在月尺度蒸散发空间插值和实测蒸发皿蒸发之间的精度对比，从表中可以看出，传统的IDW模型蒸散发空间插值计算值和实测的蒸发皿蒸散发之间的绝对误差在0.40～45.36mm之间，绝对误差的平均值为16.7mm，改进的IDW模型蒸散发空间插值计算值和实测的蒸发皿蒸散发之间的绝对误差在0.96～27.12mm之间，绝对误差的平均值为8.9mm，相比于传统的IDW模型，改进的IDW模型在蒸散发空间插值绝对误差上减少7.8mm。图4为改进前后的IDW模型蒸散发月尺度和实测蒸发皿蒸散发过程对比图，从图中可以看出，改进前后的IDW模型插值的月尺度蒸散发和实测蒸发皿蒸散发过程拟合度较高，但是改进的IDW模型插值的月尺度蒸散发和实测蒸发皿蒸散发过程拟合度明显好于传统的IDW模型。

2.3 基于改进的IDW模型的区域蒸散发空间插值结果

应用改进的IDW模型对区域蒸散发进行空间插值计算，区域蒸散发空间插值计算结果如图5所示。

图5为采用改进的IDW模型进行的区域蒸散发空间插值计算结果，从图中可以看出，区域蒸散发总体趋势为东北部大，西南部蒸散发偏小，这主要是和区域的高程分布有关，东北部高程总体上低于西南部的高程，高程高的区域，气温小，蒸散发较小，而高程低的区域，气温较高，蒸散发一般较大。