基于蚁群算法的PID参数优化

汤 伟， 冯晓会， 孙振宇， 袁志敏， 宋 梦

(1.陕西科技大学 电气与信息工程学院， 陕西 西安 710021； 2.陕西科技大学 轻工科学与工程学院， 陕西 西安 710021； 3.陕西科技大学 工业自动化研究所， 陕西 西安 710021)

基于蚁群算法的PID参数优化

汤 伟1,3， 冯晓会1,3， 孙振宇2,3， 袁志敏1,3， 宋 梦1,3

(1.陕西科技大学 电气与信息工程学院， 陕西 西安 710021； 2.陕西科技大学 轻工科学与工程学院， 陕西 西安 710021； 3.陕西科技大学 工业自动化研究所， 陕西 西安 710021)

针对常规整定方法下的PID控制器参数整定一般离不开人工经验调整，且难以得到最佳参数的缺点，提出一种基于蚁群算法的PID参数整定方法，利用Ziegler-Nichol法确定参数的搜索范围，在二次型性能指标下对PID控制器的参数进行优化，通过与Ziegler-Nichol法、单纯形法的控制效果进行对比，可以得出该整定方法得到的控制系统具有更强的抗干扰能力和鲁棒性.文中还研究了二次型性能指标可调参数 对优化结果的影响，MATLAB仿真结果表明，在二次型性能指标下控制效果更好.

蚁群算法； 二次型性能指标； PID控制器； 参数优化

0 引言

PID控制是目前应用最为广泛的控制策略，以其简单清晰的结构、良好的鲁棒性和广泛的适用范围，深受工业界的青睐，并且日益受到控制理论界的重视[1].然而，PID控制器控制效果的好坏与其参数整定有很大关系[2].常规的PID控制器参数整定的方法很多，概括起来有两大类：一是实验试凑法，它主要依赖调试经验，方法简单、易于掌握，在工程实际中被广泛采用，但根据参数凑试法得出的控制器参数的控制效果往往并不是很理想，而且手动调整控制器参数找到较优值费时又费力；二是理论计算整定法，它主要是依据系统的数学模型，经过理论计算确定控制器参数，这种方法所得到的计算数据还必须通过工程实际进行调整和修改[3-5].因此利用一种优化算法对控制器参数进行优化是非常必要的[6].

单纯形法PID控制器参数整定方法，方法简单，局部搜索能力强，具有超调小过渡平缓的控制效果，但该方法依赖初始值，且得到的结果往往响应速度不够快[7-9].蚁群算法是基于种群的启发式仿生进化算法，该算法采用的正反馈机制与分布式并行计算机制[10]，易于与其它方法结合，具有较强的收敛性和鲁棒性，特别适用于组合优化问题的求解[11].本文提出了一种基于蚁群算法的PID控制器参数整定方法，利用Z-N(Ziegler-Nichol)法确定参数的搜索范围，选用二次型性能指标作为目标函数对PID控制器参数进行优化，使系统达到最优控制.

1 蚁群算法

蚁群算法是一种基于种群的启发式搜索算法，其灵感来源于蚂蚁在寻找食物过程中发现路径的行为，蚂蚁在寻找路径时会在路径上释放出一种特殊的信息素.当它们碰到一个还没有走过的路口时，就随机地挑选一条路径前行并释放信息素.路径越短走过的蚂蚁越多，这种信息素的浓度也就越高.之后蚂蚁选择激素浓度较高路径概率就会相对较大.这样形成一个正反馈.最优路径上的激素浓度越来越大，而其它的路径上激素浓度却会随着时间的流逝而消减，最终整个蚁群会找出最优路径[12].

蚁群算法的核心思想有三条：选择机制，蚂蚁按状态转移概率进行路径选择，信息素越多的路径，得到的状态转移概率越大，被选择的可能性越高；信息素更新机制，路径越短，信息素增加越快；协作机制，蚂蚁个体之间通过信息素进行信息交流.

2 基于蚁群算法的PID参数优化

2.1 PID控制原理

PID控制系统框图如图1所示.

图1 PID控制系统框图

在PID控制器系统中，r(t)为输入量，y(t)为输出量，u(t)为控制器输出量，PID控制是按偏差e的比例、微分和积分的线性组合来控制的一种调节器，可描述为：

(1)

式(1)中：Kp为比例系数，Ti为积分时间系数，Td为微分时间系数，进一步可描述为：

(2)

式(2)中：Ki=Kp/Ti为积分系数，Kd=Kp·Kd，上式中有Kp、Ki和Kd3个参数需要确定，使得决定控制系统特性的某一性能指标达到最佳.

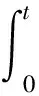
(3)

式(3)中：ρ为可调参数，一般取值范围为[0,1].

2.2 基于蚁群算法的PID参数寻优

蚁群算法优化PID参数就是寻找Kp、Ki、Kd的最优值，把Kp、Ki、Kd作为一个组合，蚂蚁在搜索空间中在信息素的指引下不断调整路径，最终找到最优的路径，最优路径所对应数值即为PID控制器的最优参数.基于蚁群算法的PID控制系统框图如图2所示.

图2 基于蚁群算法的PID控制系统框图

2.2.1 节点和路径的建立[14]

实现蚂蚁的寻优过程就要建立蚂蚁寻优所需的节点与路径.假设Kp、Ki、Kd均有4位小数，则各需要5个数字来表示，共需15个数字，根据Z-N法得到的参数值确定Kp、Ki、Kd小数点前1位，小数点后4位，每位数值的取值范围均为[0,9]，体现在OXY平面上如图3所示.其中横坐标为Kp、Ki、Kd所需的15位数字，纵坐标为每位数字可能对应的数值，15条等间距且垂直于X轴的线段ai(i=1～15)与9条等间距且垂直于Y轴的线段的交点构成所需节点，用符号C(xi,yai)表示一个节点.

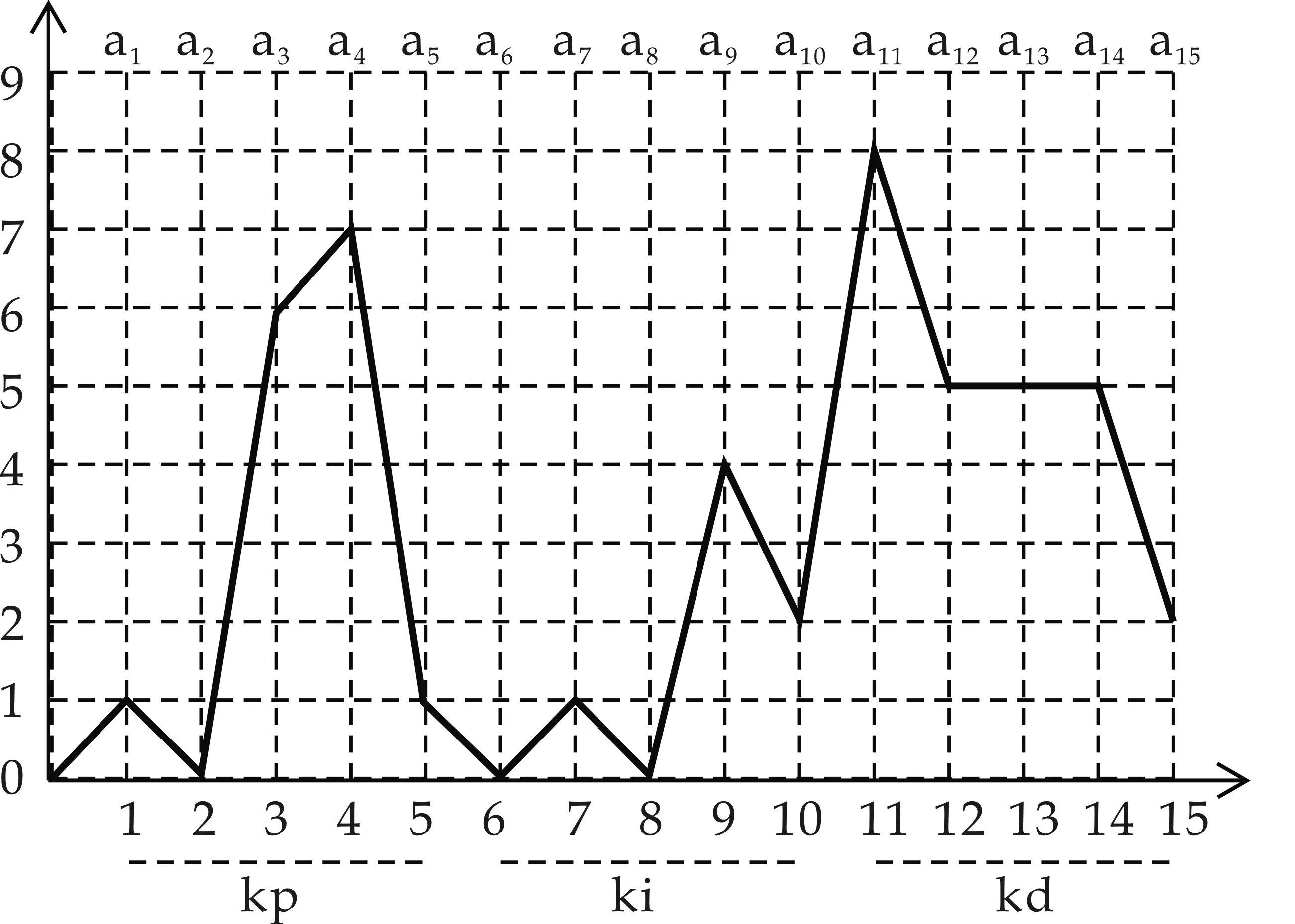
图3 节点和路径示意图

假如蚂蚁k从原点出发，当它爬行到ai线段上任意一点时，完成一次循环，蚂蚁的爬行路径可以表示为：

原点→C(x1,ya1)→C(x2,ya2)→C(x3,ya3)

→C(x4,ya4)→C(x5,ya5)→C(x6,ya6)

→C(x7,ya7)→C(x8,ya8)→C(x9,ya9)

→C(x10,ya10)→C(x11,ya11)→C(x12,ya12)

→C(x13,ya13)→C(x14,ya14)→C(x15,ya15)

其中节点C(xi,yai)在线段ai上，该路径表示的Kp、Ki、Kd的值为：

(4)

在实际设置各节点的过程中，可以利用Z-N法整定出的Kp*、Ki*、Kd*按式(5)[15]确定蚂蚁实际搜索的范围，使蚂蚁在有可能出现最优解的范围内进行搜索，加快蚁群算法的收敛速度.

(5)

式(5)中：ε为[0,1]内选定的某一数值.

2.2.2 路径选择与信息素更新

蚂蚁在搜索空间中在信息素的指引下不断选择并调整路径，恰当的状态转移概率计算方法和信息素更新方法在很大程度上决定着算法性能的优劣.

(1)本文中蚂蚁的状态转移概率按式(6)计算

(6)

式(6)中：t为当前时刻，τ(xi,yai,t)为t时刻节点C(xi,yai)上遗留的信息素，η(xi,yai,t)为t时刻节点C(xi,yai)上信息能见度，按式(7)确定，α为遗留信息量的重要程度，β为启发信息的重要程度.

η(xi,yai,t)=η(xi,yai,t)+Δη(xi,yai,t)

(7)

式(7)中：Δη(xi,yai,t)为t时刻节点C(xi,yai)上信息能见度的变化量，按式(8)确定.

(8)

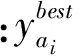
(2)节点信息素更新按式(9)确定

τ(xn,yan,t)=(1-γ)τ(xn,yan,t)+Δτ(xn,yan,t)

(9)

式(9)中：γ为信息素挥发系数，Δτ(xn,yan,t)为t时刻节点C(xi,yai)上的信息素的总变化量，按式(10)确定.

(10)

式(10)中：Δτ(xi,yai,t)为每只蚂蚁爬过后节点C(xi,yai)上的信息素的变化量，按式(11)确定.

(11)

式(11)中：Q为信息素强度.

2.2.3 基于蚁群算法的PID参数优化步骤

(1)初始化

①生成节点矩阵，设置蚁群规模m，遗留信息素的重要程度α，启发信息的重要程度β，信息素挥发系数γ，信息素强度Q，最大迭代次数NC_max；

②设置遗留信息素τ和信息素能见度η为常量；

(2)寻优

①将蚂蚁放在原点，开始爬行，按式(6)计算待访问的各节点的状态转移概率P；

②rand生成[0,1]内的随机数，寻找状态转移概率大于该随机数的节点，选择第一个作为下一个爬行的节点；

③当蚂蚁爬过ai线段上任意一点时，完成一次循环，记录爬过的节点的纵坐标；

④当全部蚂蚁完成一次爬行，按式(4)计算Kp、Ki、Kd，并赋给PID控制器；

⑤运行控制系统模型，得到目标函数值，并返回，记录本次最优结果；

(3)按式(9)更新信息素，NC=NC+1；

(4)进入下一次循环直到到达NC_max，输出最优Kp、Ki、Kd，具体程序流程图如图4所示.

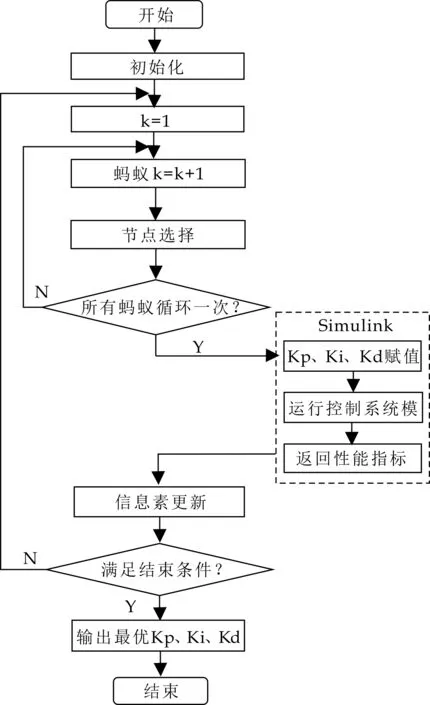
图4 程序流程图

3 仿真结果分析

在MATLAB中进行仿真实验，在Simulink中建立PID控制系统模型，运行蚁群算法m文件调用PID控制系统模型，给Kp、Ki、Kd赋值，运行PID控制系统模型并返回目标函数值，为蚁群算法判断当前结果的优劣提供依据，从而寻找最优结果.采用二次型性能指标的PID控制系统模型如图5所示.

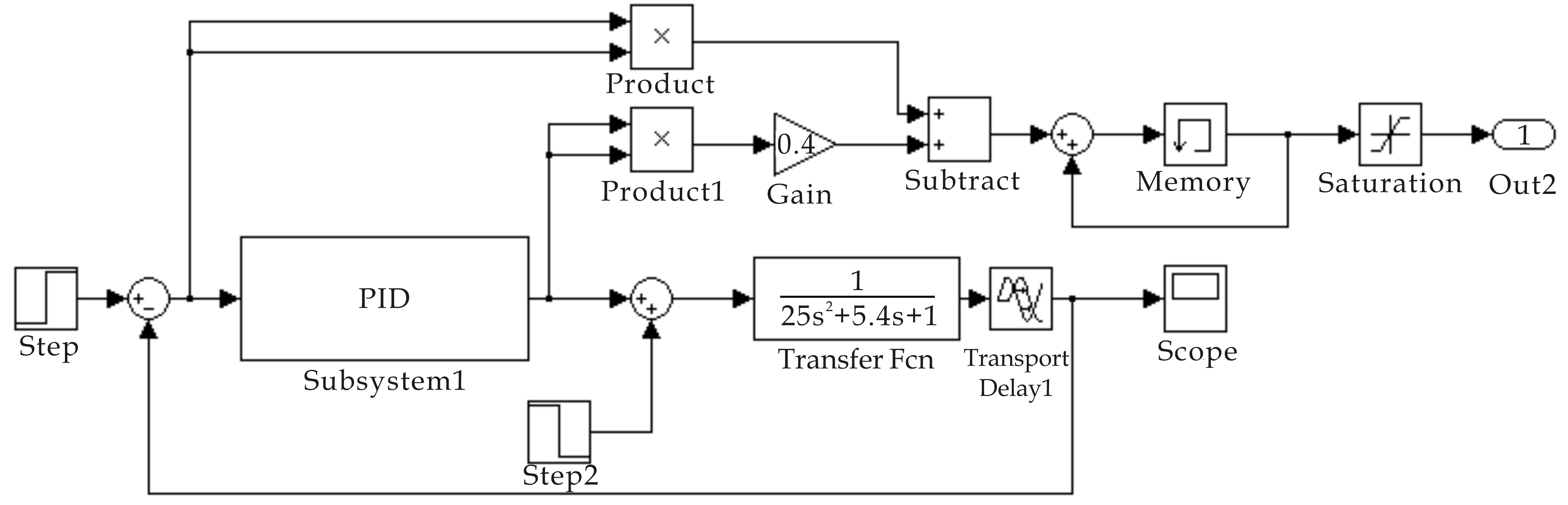
图5 PID控制系统模型

(1)在控制工程中二阶系统极为普遍，而且不少高阶系统的特性在一定条件下可用二阶系统的特征来表征，所以选取二阶系统作为被控对象具有较大的实际意义.本文选取的带有时滞环节的二阶系统为被控对象，该系统阻尼系数ζ=0.54，自然震荡频率ωn=0.2，为欠阻尼二阶系统，在单位阶跃信号下，系统响应表现为衰减震荡，超调量为30%，调节时间约为250 s.

为了验证本文提出的蚁群算法的优越性，本文将该优化方法的结果与Z-N法、单纯形法的控制效果进行对比分析.利用Z-N法得到的PID控制参数为Kp=1.768 9，Ki=0.202 1，Kd=3.715 5，利用单纯形法得到的PID控制参数为Kp=0.835 0，Ki=0.129 2，Kd=8.787 0[16].对于蚁群算法时，设置各参数为：m=10，NC_max=20，α=1，β=1.5，γ=0.1，Q=10，ρ=0.4，ε=0.5.在第2 s给定一阶跃为1的输入信号，使整个系统运行，并在110 s加入幅值为0.2扰动，得到的最优控制参数为Kp=1.107 4，Ki=0.119 3，Kd=7.130 5.系统响应曲线如图6所示.

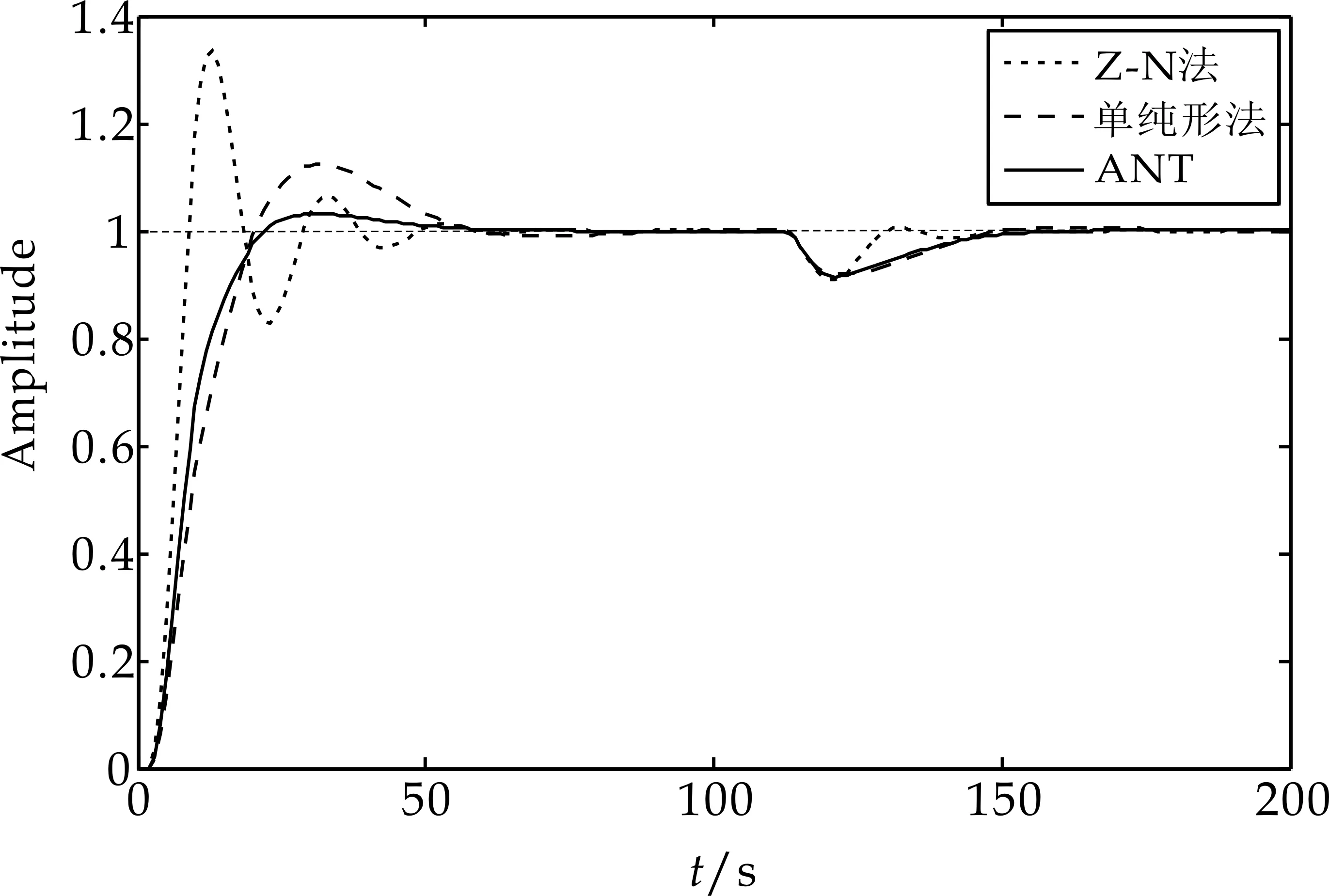
图6 系统响应曲线图

三种方法的系统动态性能参数和系统抗扰性能参数如表1和表2所示.

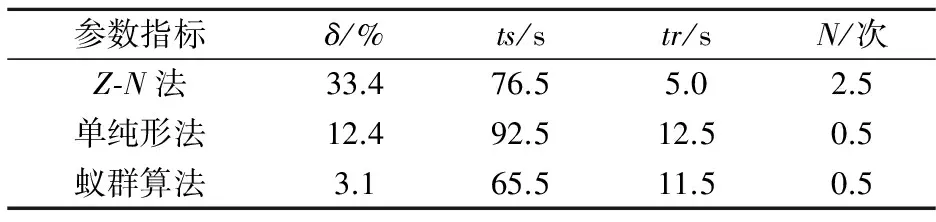
表1 系统阶跃响应性能分析

表2 系统抗扰性能分析

表1中列出超调量δ、调整时间ts、上升时间tr以及震荡次数N，表2列出了系统扰动调节时间tv和系统的动态降落△y.由表中数据可以看出利用Z-N法得到的PID控制系统响应最快，但却出现了极大的超调量和强烈的波动，利用单纯形优化方法得到的PID控制系统相比于Z-N法，有较小的超调量和动态降落，且过渡平稳，控制效果较好，但上升时间、调整时间以及扰动调节时间均变长，而利用蚁群算法得到的PID控制系统不仅阶跃响应上升和扰动响应速度快，而且超调量明显减少且过渡平稳，体现出更快的响应速度与更好的抗干扰性.

(2)为了保证控制系统的效果，改变系统模型的部分参数，分别取ζ=0.76，ωn=0.2和ζ=0.25，ωn=0.2比较三种方法在模型失配的情况下的适应能力.仿真效果如图7和图8所示.

图7 模型失配ζ=0.76时系统响应曲线图

图8 模型失配ζ=0.25时系统响应曲线图

由图7可以看出,当阻尼系数增加时单纯形法的控制效果略有下降，出现了轻微波动，同时超调量也变大，而Z-N法和蚁群算法的控制效果变好，但Z-N法得到的PID控制系统仍存在较大超调量，调节时间长，蚁群算法得到的PID控制系统超调量为0，响应速度也变快，控制效果更好.

由图8可以看出,当阻尼系数减小时，Z-N法得到的PID控制系统出现了剧烈震荡，相比之下单纯形法得到的PID控制系统和蚁群算法得到的PID控制系统超调量只是略微增加，调节时间稍有变长，但单纯形优化方法得到的PID控制系统出现轻微的波动，蚁群算法得到的PID控制系统调整时间短、超调小、过渡平稳，控制效果更好.因此，蚁群算法得到的PID控制系统体现出更好的鲁棒性.

(3)为了研究基于蚁群算法的PID参数优化方法的适应范围，选取带有滞后环节的一阶系统作为被控对象进行仿真实验：

取τ=2和τ=5，分别构成小时滞系统和大时滞系统，其仿真效果如图9和图10所示.

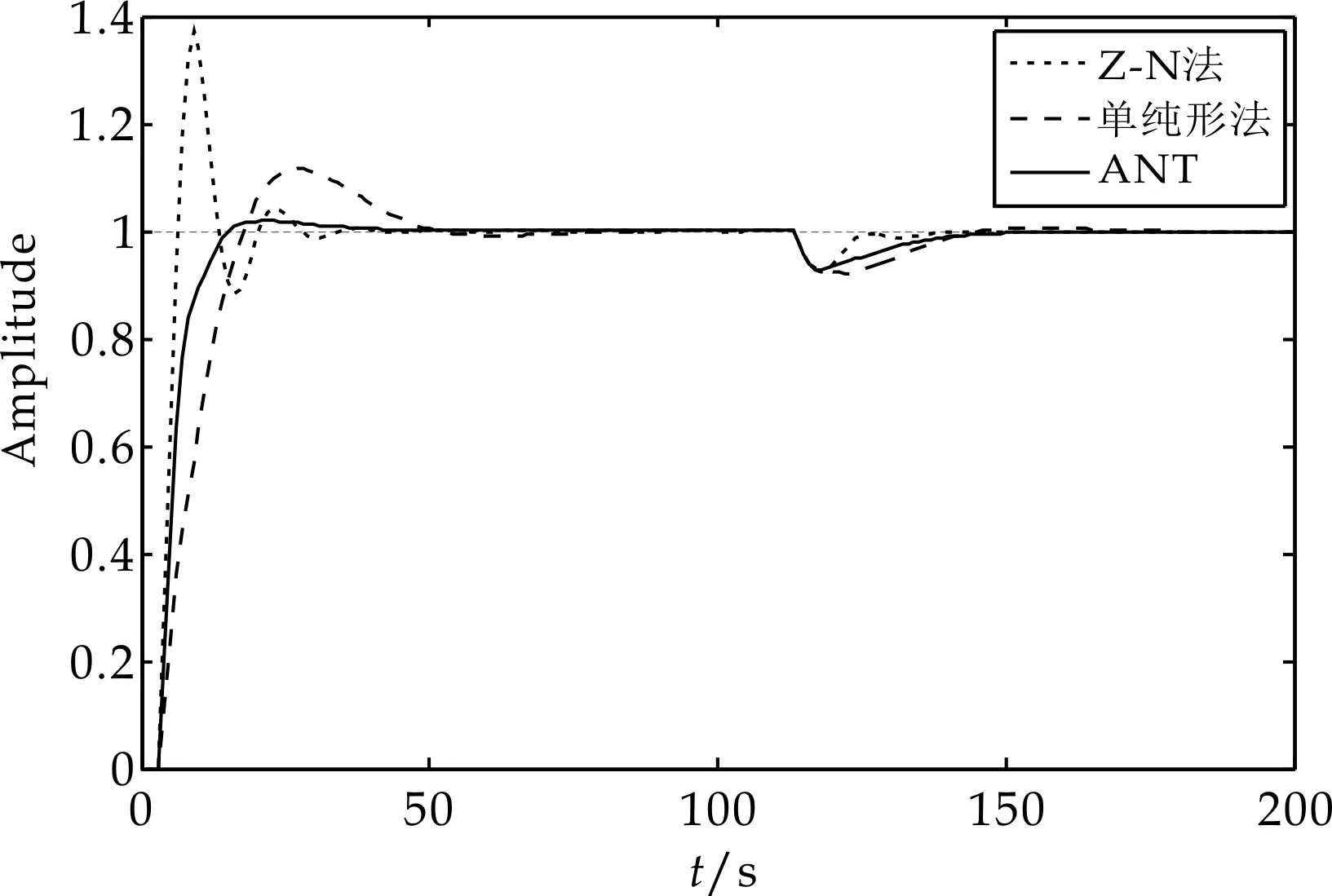
图9 一阶小时滞系统响应曲线图

图10 一阶大时滞系统响应曲线图

从图9可以看出,对于小时滞系统，由蚁群算法得到的PID控制系统超调量小，响应迅速，过渡平稳，

具有更好的控制效果；由图10可以看出,对于大时滞系统三种方法的控制效果都不是很理想，但三者之中蚁群算法得到的PID控制系统仍具有最好的控制效果.

通过以上的比较，从响应性、抗干扰性、鲁棒性和适应性这几个方面的比较可以得出结论，蚁群算法得到的PID控制系统具有更好的性能.

(4)为了研究二次型性能指标常数ρ对优化结果的影响，以二阶系统为被控对象，令ρ值分别为0，0.2，0.4，0.6，0.8，1，利用蚁群算法得到对应的最优PID控制参数，进而得到系统响应曲线如图11所示，图中ρ表示为rou.

由图11可以看出，当ρ=0，即忽略控制信号影响时，系统阶跃响应最快，响应曲线峰值和超调量均最大，震荡严重.随着ρ的增加，系统阶跃响应变慢，调节时间变长，响应曲线峰值和超调量逐渐减小，但当ρ到某个值时，系统响应曲线峰值和超调量均逐渐增大，再次出现轻微震荡现象，对于该被控对象ρ在[0.2,0.4]的范围内取值可以得到较好的控制效果.所以控制信号以合适的比重对系统产生作用时，系统有最好的性能，比重过大或者过小，都难以取得好的控制效果.

图11 不同ρ值下的系统响应曲线图

4 结论

本文提出的基于蚁群算法的PID参数整定方法，充分利用了Z-N法的内核，可以快速准确地找到PID控制器的最佳参数，从响应性、抗干扰性、鲁棒性和适应性这几个方面的比较可以得出结论，蚁群算法得到的PID控制系统具有更好的性能，该整定方法为PID控制器参数的人工经验调整提供了一种有效的替代方法.对二次型性能指标可调参数ρ对优化结果影响的研究得出采用蚁群算法优化后的结果的好坏,除了取决于算法本身外，还取决于所选用的性能指标，合适的性能指标有利于找到更适合工程应用的最优解.

[1] 杨 智,朱海锋,黄以华,等.PID控制器设计与参数整定方法综述[J].化工自动化及仪表,2005,32(5):1-7.

[2] 王 伟,张晶涛,柴天佑,等.PID参数先进整定方法综述[J].自动化学报,2000,26(3):347-355.

[3] 魏 韡,梅生伟,张雪敏,等.先进控制理论在电力系统中的应用综述及展望[J].电力系统保护与控制,2013,41(12):143-153.

[4] 杨 智.工业自整定PID调节器关键设计技术综述[J].化工自动化及仪表,2000,27(2):5-10.

[5] 李军军,吴燕翔,甘世红,等.基于梯度PSO算法的PID参数整定[J].科学技术与工程,2009,9(9):2 463-2 467.

[6] Comions P,Munro N.PID controller tuning methods and design to specification[J].IEE Proceedings Control Theory and Applications,2002,149(1):46-53.

[7] 朱学贵,王 毅,昝建明,等.基于单纯形法的神经元PID控制器学习参数优化[J].系统仿真学报,2006,18(11):3 030-3 033,3 037.

[8] 张 磊.基于单纯形法的PID控制器的最优设计[J].信息与控制,2004,33(3):376-379.

[9] 刘晓谦,王 勇,穆顺勇,等.基于单纯形法的PID控制器参数优化设计[J].计算机仿真,2004,21(11):191-193,227.

[10] 石 钊,葛连升.一种解多QoS约束组播问题的改进蚁群算法[J].山东大学学报(理学版),2007,42(9):41-45.

[11] 吴 斌,史忠植.一种基于蚁群算法的TSP问题分段求解算法[J].计算机学报,2001,24(12):1 328-1 333.

[12] 段海滨.蚁群算法原理及其应用[M].北京:科学出版社,2005.

[13] 刘长良,马增辉,开平安,等.基于间隙度量和二次型优化的电站主汽温控制[J].中国电机工程学报,2014,34(32):5 771-5 778.

[14] 李 静,刘 学,赵 健,等.基于蚁群寻优的汽车牵引力PID控制参数整定[J].吉林大学学报(工学版),2008,38(4):769-772.

[15] 詹士昌,吴 俊.基于蚁群算法的PID参数优化设计[J].测控技术,2004,23(1):69-71,75.

[16] 王 伟,于军琪.基于单纯形法的最优PID控制器设计[J].装备制造技术,2009(6):77-78,141.

【责任编辑：蒋亚儒】

Parameters optimization of PID controller based on ant colony algorithm

TANG Wei1,3， FENG Xiao-hui1,3， SUN Zhen-yu2，3， YUAN Zhi-min1,3， SONG Meng1,3

(1.College of Electrical and Information Engineering, Shaanxi University of Science & Technology, Xi′an 710021, China; 2.College of Bioresources Chemical and Materials Engineering, Shaanxi University of Science & Technology, Xi′an 710021, China; 3.Industrial Automation Institute, Shaanxi University of Science & Technology, Xi′an 710021, China)

To solve the problem that the conventional tuning method for the PID controller needs extra adjustments based on human experience and it is difficult to get the best parameters,a PID parameters tuning method based on ant colony algorithm is presented,in which Ziegler-Nichol method tuning is used to determine the search range and the parameters of the PID controller is optimized under the quadratic performance index.Compared with the effects of Ziegler-Nichol method and simplex method,this method shows a stronger anti-jamming ability and robustness.Besides,the influence of the adjustable parameter of the quadratic performance index on the optimization results is studied.The MATLAB simulation results show that the control effect is better under the quadratic performance index.

ant colony algorithm; quadratic performance index; PID controller; parameters optimization

2016-12-11 基金项目：陕西省科技厅重点科技创新团队计划项目(2014KCT-15)； 陕西省科技厅科技统筹创新工程计划项目(2016KTCQ01-35)

汤 伟(1971-)，男，河南信阳人，教授，博士，研究方向：工业过程高级控制、大时滞过程控制及应用

1000-5811(2017)02-0147-07

TP273

A