高中数学教学逆向思维能力的培养策略分析

罗树

摘要：实现高中生素质全面的发展，是全新的教育体制下对学生的基本要求。新课标对高中数学提出了更高的要求，高中数学课堂通过对学生逆向思维的有效培养，继而激发学生的创新能力和学习积极性，提高教学质量。本文针对高中数学教学逆向思维能力的培养进行了分析，提出有效的措施，从而为逆向思维的培养提供参考。

关键词：高中数学；教学；逆向思维能力；培养；策略

高中数学知识具有复杂性和系统性，对学生思维能力的培养具有重要意义，然而，教师按部就班的对学生予以引导，将导致学生的形成思维定势，因而造成学生对于数学知识的本质未能有深入的理解。通过对学生逆向思维的培养，有利于学生对数学知识有正确的认知，并促进学生创新思维的发展。因此，在高中数学教学期间，必须对逆向思维的培养，从而有助于数学教学质量的提高。

一、逆向思维的内涵

所谓逆向思维，与正向思维相反，其作为一种创新型思维，打破了常规的思维程序，与正向思维的根据原因推理结果截然不同，是从相反的方向采取全新的思维对问题进行分析，从而得出结论。

通常情况下，逆向思维类型分为三种，分别是缺点逆向思维法、转换型逆向思维法和反转型逆向思维法[1]。同时，逆向思维具有异常性、普遍性和新颖性等特点，所以逆向思维作为一种分析方法，在解决问题时，对问题的处理有着一定的作用。

另外，在逆向思维的培养过程中，应当对其类型和特点等有全面的掌握，进而为逆向思维的培养提供有利依据。总之，逆向思维对习惯性思维进行突破，从其他角度探析问题，进而容易找到解决问题的突破口，对解决一些问题具有重要意义。尤其是在教学过程中，通过采取逆向思维，能够促进学生对知识的深入理解，然后掌握相关规律，对原有的思想进行创新，进而为教学质量的提升奠定良好基础。

二、培养逆向思维的方法

（一）综合法

对于综合法，其有助于对逆向思维的良好培养，在利用综合法时，需将要推论的结果作为起始点，逆向根据已知条件作为出发点，然后结合相关概念和定义对问题进行逐一分析和推导，层层推进，直到找到结果为止。运用此法时，要从原因出发，然后按照一定的线索对结果加以探讨，直到找到最佳结果为止。

（二）逆推法和分析法

在培养逆向思维期间，可以采取不同的方法，通常情况下，比较直接的方法就是逆推法，也称之为反向逆推法（也称“分析法”），以反向逆推的方式对命题的逆命题加以判定。对于逆推法而言，其并不适用于解决各种问题，逆向思维的本质并不是将容易解决的问题进行具体化处理，通过采用逆向思维方法，进而找到最佳和比较简便的方法，所以在教学过程中，为了使得教学取得良好的效果，在采取逆推法时，需要对该方法予以全面的认知，避免将逆向思维予以复杂化，使得通过运用逆向思维对问题予以有效解决。

三、在高中数学教学时培养逆向思维能力的重要性

在高中数学教学过程中，为了有助于调动学生分析问题和解决问题的积极性，并培养学生的创新能力，应党培养逆向思维能力，进而有利于学生找到解答问题的突破口[2]。由于思维过程的指向性有区别，思维分为正向思维和逆向思维，在高中数学教学期间，运用正向思维解决问题，虽然解答效率高，但长期下来将导致学生的思维具有局限性，对一些特殊问题难以有效解答。

四、高中数学教学培养逆向思维能力的有效措施

（一）充分运用多媒体展开教学

在高中数学教学过程中，为了促进数学教学质量的提升，并有利于培养学生的思维能力，应当加强对学生的逆向思维能力的培养，从而为高中数学教学有效性的增强创造良好的条件。在培养逆向思维期间，教师需要充分运用多媒体展开教学，继而为逆向思维的有效培养提供良好的途径。

例如，在人教版高中数学“直线与平面平行的判定定理”教学时，教师为了学生更加深入的理解该定理，将推导过程用多媒体的形式向学生展示，使得学生在直观作用下理解数学知识。

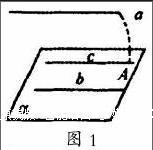
如果直线在平面外，那么，直线可以与平面相交或者是平行，但直线和平面不相交，以正向思维方式解决问题，由于可依据的条件和定理比较少，则需要采取逆向思维方式。其中，图1是假设的直线与平面不相交的图形，假设 ，由于 // ，因而 ，此时，在 平面内，可以作直线c，使得直线c//b，根据 ，a//c，因而与 相互矛盾[3]。因此， 的假设不成立，所以 。

总之，在高中教学过程中，教师为了培养学生的逆向思维能力，借助于直观教学法，使得学生对逆向思维有感性和直观感觉上的认知，进而为其理性的解答数学知识打下坚实基础[4]。同时，对学生的逆向思维培养具有重要意义。

（二）在学习数学概念时培养逆向思维

在高中数学教学期间，为了进一步提升数学教学效果，教师应当注重对学生逆向思维的培养，使得在一定程度上促进学生的综合能力得到增强，对其学生数学知识创造有利条件。

在开展教学活动时，有些问题难以有效解决，必须通过运用逆向思维，对不能顺利解决的问题加以处理。

在高中数学教学内容中，概念是学生学习数学知识的基础，学生只有对概念有深层次的理解，才能有利于数学知识的解答。通常情况下，概念是以一句话的形式对相关内容的概括，可以将客观事物的真实属性反映出来，所以教师在概念教师时在培养学生正向思维的同时，对学生逆向思维的培养予以高度重视。比如，在讲解“映射”概念过程中，假想A→B是集合A到集合B的映射，判定集合A和集合B中各个元素的对应关系。教师以逆向思维的方式引导学生，集合A中的元素没有剩余，而且每个元素在个集合B相对应时，具有唯一的象，那么，集合B中还有剩余元素，也就是集合B中的元素未能在集合A中找到原像，可以得出在映射的对应形式有很多种，包含了一一对应和多对一。但是，不存在一对多的形式。总之，通过逆向思维的方式实现了对概念的有效学习，对高中数学教学活动的开展奠定了良好基础。

结束语 ：

教师通过培养学生的逆向思维，以全新的视角分析问题，通过将结论作为出发点，以全新的视角分析和处理问题，继而打破学生的思维定式，因而以灵活和有效的方式解答数学问题。另外，加强对学生逆向思维的培养，对学生综合素质的提升具有重要意义。因此，在高中数学教学期间，培养逆向思维能力，对学生分析和深入理解数学知识起到举足轻重的作用，在教学期间，教师为促进学生对知识的全面理解，并拓宽学生的学习思路，应当在培养学正向思维的同时，加强对学生逆向思维的培养，进而有助于学生分析和处理问题。

参考文献：

[1]孙艳松.高中数学教学逆向思维能力的培养[J].科技视界，2014（2）：243-243.

[2]黄恩祥.高中数学教学中逆向思维能力的培养[J].學园，2014（21）：149-149.

[3]张恩祥.试论逆向思维在高中数学中的应用[J].理科爱好者（教育教学版），2012，4（4）：38.

[4]况安永.例说高中数学教学中逆向思维能力的培养[J].文理导航（中旬），2014（3）：25-25.