陶瓷涂层厚度的水浸超声谐振测量

李永杰，韩赞东

(清华大学 先进成形制造教育部重点实验室 摩擦学国家重点实验室，北京 100084)

陶瓷涂层厚度的水浸超声谐振测量

李永杰，韩赞东

(清华大学 先进成形制造教育部重点实验室 摩擦学国家重点实验室，北京 100084)

采用水浸超声谐振方法，结合全相位频谱分析技术，对304不锈钢基体上的厚度在1 mm以下的氧化铝陶瓷涂层的厚度进行测量。结果表明：基于全相位频谱分析技术的水浸超声谐振方法测得的涂层厚度与实际厚度的相对误差小于2%，可以较为精确地实现对氧化铝涂层厚度测量。

陶瓷涂层；厚度测量；超声谐振；全相位技术

金属材料具有较好的强度、韧性、硬度、塑性、疲劳强度等性能，被广泛应用于生产中。陶瓷材料在耐高温、耐腐蚀、耐磨损等性能方面显著优于金属材料。在金属基体上涂覆陶瓷材料，可以充分发挥陶瓷材料的特点，与金属材料起到优势互补的作用[1-2]。比如发动机叶片上的热障涂层，就是在金属叶片上涂覆一层非金属陶瓷材料，以起到阻碍热量向叶片传导的作用。

涂层的厚度是涂层质量的重要指标，以热障涂层为例，航空发动机叶片对涂层厚度的精度要求很高，厚度偏薄会导致叶片隔热效果降低，厚度不均匀会导致叶片受热不平衡，产生热应力[3-5]。此外，位于热障涂层与基体之间的黏接层的厚度对陶瓷层的黏接质量有很大的影响。

涂层厚度检测包括电磁检测[6]、微波检测[7]、超声检测[8-12]等方法。超声检测因具有灵敏度高、穿透能力强、检测范围广等优点而被广泛应用。国内外许多大学和研究机构对涂层质量的超声检测进行了研究。廖欢[8]等利用超声水浸聚焦检测法，通过对接收到的信号进行傅里叶分析，推导出涂层厚度与频谱特征量的关系，用于涂层厚度的检测；孙颖[9]等利用有限元仿真和试验的方法对波包分解技术进行了研究，并将其应用于热障涂层陶瓷层厚度检测中；郑金华[10]等结合频谱分析法、WTMM(小波变换模极大值)分析法和 Lipschitz指数法检测信号奇异性的原理，提出了三种热障涂层陶瓷厚度检测的方法，并取得了较好的检测效果；赵扬[11]等利用声压反射系数幅度谱，测量了聚氯乙烯基体上铝质涂层的厚度，揭示了介质声阻抗与频谱的关系；林祺[12]等提出了一种基于Welch功率谱估计技术的涂层厚度检测方法，相对于传统傅里叶变换，Welch功率谱更容易实现厚度的检测。

以上文献中均用到了频谱分析，尤其是傅里叶变换。笔者在传统傅里叶变换的基础上，结合全相位分析技术对信号进行分析，得到了准确的频谱信息。全相位频谱分析技术是为了减小由于数据截取造成的傅里叶变换频谱泄漏而提出的谱分析方法。相对于传统的离散傅里叶变换频谱分析方法，全相位频谱分析技术可以有效抑制频谱中的旁瓣信号，减少频谱泄漏。

笔者采用水浸超声检测方法，利用水作为超声从激励源到试样的传播介质和耦合剂，对304不锈钢上的氧化铝陶瓷涂层的厚度进行检测。检测结果表明：基于全相位频谱分析技术的超声谐振方法测得的涂层厚度与实际厚度的相对误差小于2%，可以较为精确地实现对氧化铝涂层厚度的测量。

1 基本原理

水浸超声检测原理如图1所示(H为探头距离试样上表面的距离，d1为涂层的厚度，c1为水中的声速，c2为涂层中的声速，c3为黏接剂中的声速)，采用直入射自发自收方式对涂层试样进行检测。超声探头接收到的信号是涂层上表面的反射波与声波透射到涂层后得到的多次反射信号的叠加。

图1 水浸超声检测原理示意

由于超声波在涂层上表面的反射信号ur1(t)幅值较大，若对整个波形进行傅里叶分析，则其幅值谱将被ur1(t)的幅值谱覆盖，且ur1(t)不包含涂层厚度信息，因此实际分析中，将ur1(t)排除在分析范围之外，即取:

(1)

利用傅里叶变换的线性，可以得到接收探头接收到的反射波叠加信号:

(2)

式中：rmn为从介质m到介质n的声压反射系数；ω为角频率。

R(ω)的幅值与相位分别为:

(3)

(4)

(5)

此即为超声波在涂层中的谐振频率。利用上式，可以得到氧化铝陶瓷片厚度的计算公式：

(6)

式中：Δf为频谱中两相邻极大值的频率间隔。

由于傅里叶变换所用的数据是截取自示波器采集数据的某一段数据点，在进行傅里叶变换时会产生频谱泄漏等问题。天津大学的王兆华教授等[13-16]提出的全相位DFT(离散傅里叶变换)频谱分析方法，可以有效地抑制旁瓣泄漏，减小截断造成的频谱分析误差。

传统频谱分析是截取连续数据点x(0),x(1),…,x(N-1)作DFT实现的，而全相位DFT的分析对象则是包含x(0)的N组数据分段：

将式(7)的分段xn(n=0,1,…,N-1)中的数据点循环左移，使得每个分段中的x(0)位于最左侧，得到新的分段，称为全相位分段：

(8)

对式(8)中的全相位分段分别进行FFT频谱分析，将分析的结果进行加权求和，即可得到全相位谱分析的结果。

2 试验过程

2.1 试样制备

试样采用304不锈钢作为金属基体，氧化铝陶瓷片作为涂层，氰基丙烯酸酯作为黏接剂。陶瓷片厚度分别为0.25，0.35，0.50，0.67，0.77 mm，分别进行超声谐振厚度测量。如图2为涂层厚度检测试样外观。

图2 涂层厚度检测试样外观

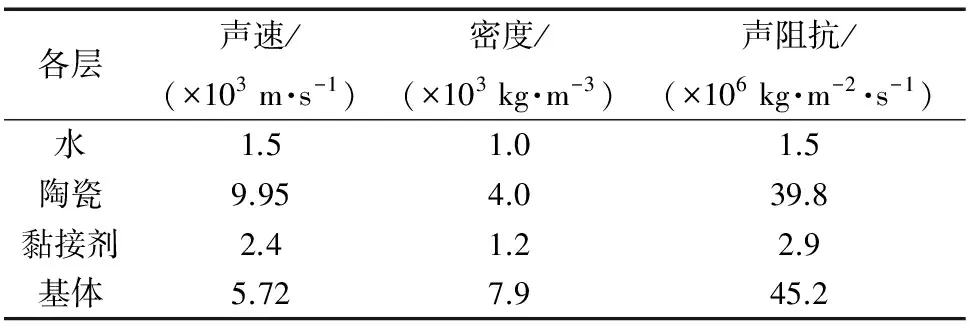
超声波激励信号为方波信号，采用水浸超声检测方式，水浸超声检测系统如图3所示，水浸超声检测试样各层结构材料的声学参数见表1。

图3 水浸超声检测系统外观

各层声速/(×103m·s-1)密度/(×103kg·m-3)声阻抗/(×106kg·m-2·s-1)水1．51．01．5陶瓷9．954．039．8黏接剂2．41．22．9基体5．727．945．2

水浸超声检测系统如图3所示，超声激励装置为OLYMPUS 5077，超声信号采集装置为Tektronix示波器。示波器采集的时域信号经过计算机处理得到频域信号，用于后续的厚度计算及黏接质量评估。

2.2 厚度检测

使用如图3所示的检测系统，为了增加薄层检测的灵敏度，使用15 MHz的水浸超声探头作为超声发射源，探头中心频率的实测值为17.27 MHz。水浸超声厚度检测中，不同厚度的氧化铝陶瓷涂层的波形信号基本类似。厚度为0.5 mm的涂层的超声时域信号如图4所示。

图4 厚度0.5 mm涂层的超声时域信号

图4中，区域Ⅰ主要是氧化铝陶瓷涂层的上表面回波，区域Ⅱ是超声波在涂层中若干次反射后被超声探头接收到的信号。区域Ⅱ的信号包含涂层厚度的信息，而区域Ⅰ的信号对于厚度检测没有贡献，且由于其幅值较大，对于后续数据处理的结果有很大的干扰，因此在实际的数据处理中仅对区域Ⅱ的信号进行分析。

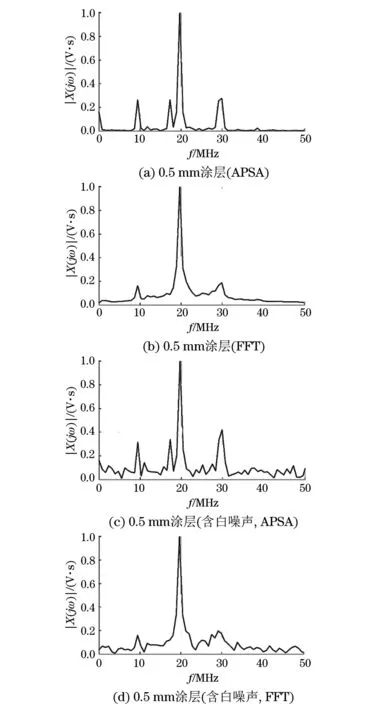
图5 0.5 mm厚涂层的超声信号的归一化频谱

3 结果与分析

图5(a),(b)为厚度0.5mm的涂层频谱，可以明显看出在10,20,30MHz附近有三个峰值。此外，在17MHz附近有一个峰值，这是探头的中心频率造成的峰值。图5(c)，(d)是厚度0.5mm涂层的回波信号加入幅值为0.25的白噪声之后的频谱，图5(c)中频谱是采用APSA方法得到的，可以明显看出上述三个峰值，而图5(d)中除了20MHz附近的峰值外，其余两个峰值不明显。比较图5(a)，(b)可以看出，全相位频谱分析方法得到的频谱相对于传统傅里叶变换得到的频谱，旁瓣抑制较为明显。比较图5(c)，(d)可以看出，全相位频谱分析方法相对于传统傅里叶变换得到的频谱拥有更高的信噪比，峰值位置更加明显，更有利于涂层厚度的检测。

笔者使用全相位频谱分析得到的频谱峰值信息，利用式(6)对不同厚度的陶瓷涂层进行厚度计算，结果列于表2。

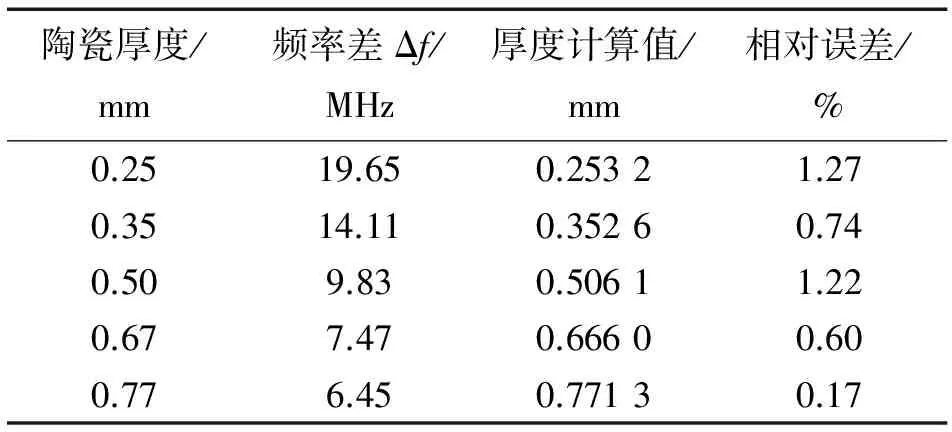
表2 陶瓷涂层厚度计算值

从表2可以看出，陶瓷涂层厚度的计算结果与实际值的相对误差小于2%，具有较高的精度，且随着涂层厚度的增加，相对误差呈下降趋势。

4 结论

(1) 水浸超声谐振方法对于亚毫米量级的薄陶瓷涂层的厚度检测具有较高的精度，可以满足一般工程检测要求。

(2) 全相位频谱分析技术可以减小由于数据截取造成的傅里叶变换频谱泄漏，有效抑制旁瓣，并且可以提高频谱的信噪比，提高涂层厚度检测的精度。

[1] 周健儿,李家科,江伟辉. 金属基陶瓷涂层的制备、应用及发展[J]. 陶瓷学报,2004,25(3):179-185.

[2] 张鹏, 朱强, 秦鹤勇, 等. 航空发动机用耐高温材料的研究进展[J]. 材料导报, 2014, 28(11): 27-31.

[3] 撒世勇,王大伟. 热障涂层材料与技术的研究进展[J]. 腐蚀科学与防护技术,2014, 26(5):479-482.

[4] VAβEN R, JARLIGO M O, STEINKE T, et al. Overview on advanced thermal barrier coatings[J]. Surface and Coatings Technology, 2010, 205(4): 938-942.

[5] 钟志春. 热障涂层表面开裂与界面剥离失效的声发射定量评价[D]. 湘潭:湘潭大学, 2013.

[6] YONG L, CHEN Z, MAO Y, et al. Quantitative evaluation of thermal barrier coating based on eddy current technique[J]. NDT & E International, 2012, 50(9): 29-35.

[7] 何存富, 杨玉娥, 吴斌. 反射系数法微波检测热障涂层厚度的实验研究[J]. 仪器仪表学报, 2011, 32(11): 2590-2595.

[8] 廖欢. 热障涂层质量超声检测研究[D]. 南昌:南昌航空大学, 2012.

[9] 孙颖. 涡轮叶片热障涂层结构状态超声检测方法研究[D]. 南昌:南昌航空大学, 2013.

[10] 郑金华. 基于超声的热障涂层厚度检测方法研究[D]. 南昌:南昌航空大学, 2014.

[11] 赵扬.超声体波声压反射系数谱表征表面涂层研究[D]. 大连:大连理工大学, 2010.

[12] 林祺. 涂层性能的超声无损检测与表征技术研究[D]. 北京:北京理工大学, 2015.

[13] 王兆华, 侯正信, 苏飞. 全相位 FFT 频谱分析[J]. 通信学报, 2003(24): 16-19.

[14] 黄翔东. 全相位数字信号处理[D]. 天津：天津大学博士学位论文, 2006.

[15] 侯正信, 王兆华, 杨喜. 全相位 DFT 数字滤波器的设计与实现[J]. 电子学报, 2003, 31(4): 539-543.

[16] 吴国乔，王兆华. 基于全相位的零相位数字滤波器的设计方法[J]. 电子与信息学报,2007,29(3):574-577.

Ultrasonic Resonance Measuring for the Thickness of Ceramics Coatings

LI Yong-jie, HAN Zan-dong

(State Key Laboratory of Tribology, Key Laboratory for Advanced Materials Processing Technology, Ministry of Education, Tsinghua University, Beijing 100084, China)

Water immersion ultrasonic resonance method was used, together with the all-phase spectrum analysis (APSA) technique, to detect the thickness of the thin layer of alumina ceramics on the 304 stainless steel substrates in the thickness less than 1 mm. The results show that the relative error of coating thickness by APSA-based ultrasonic resonance technique method is less than 2%, which means this method can measure the thickness of thin alumina layer more accurately.

Ceramics layer; Thickness measuring; Ultrasonic resonance; APSA technique

2016-08-31

李永杰(1990-)，男，硕士，主要从事超声和涡流无损检测工作。

韩赞东，E-mail:hanzd@tsinghua.edu.cn。

10.11973/wsjc201703001

TG115.28；TB553

A

1000-6656(2017)03-0001-04