基于小样本数据的构件疲劳破坏全寿命区S—N曲线

盛兴旺，郑纬奇，雷佶洲,2

(1.中南大学 土木工程学院，湖南 长沙　410075；2.中交城市轨道交通设计研究院有限公司，湖北 武汉　430056)

S—N曲线模型是描述在给定平均应力、最小应力或应力比的情况下，最大应力或应力幅与疲劳寿命的关系，一般用于表征材料或构件的疲劳性能[1]。目前，国内外相关标准中采用的S—N曲线模型主要有以下4种：①单对数线性模型，即S—lgN模型，如图1(a)所示，GB/T 24176—2009《金属材料疲劳试验数据统计方案与分析方法》[2]中采用了该模型，该模型主要适用于构件疲劳破坏的中等寿命区；②双对数线性模型，即lgS—lgN模型，如图1(b)所示，JGJ/T 27—2014《钢筋焊接接头试验方法标准》[3]中采用了该模型，该模型主要适用于构件疲劳破坏的中等寿命区；③双对数多折线模型，即lgS—lgN两段或三段折线模型，如图1(c)所示，BS—EN 1993-1-9-2005《Eurocode 3:Design of Steel Structures—Part 1—9:Fatigue》[4]中采用该模型，该模型用于构件疲劳破坏的中、长寿命区；④三参数幂函数模型，即P—S—lgN模型，如图1(d)所示，MIL-HDBK-5J《Metallic Materials and Elements for Aerospace Vehicle Structures》[5]中采用了该模型，该模型主要用于构件疲劳破坏的中、长寿命区。其中，单对数线性模型和双对数线性模型使用方便，概念清晰，求解简单，但其不适用于构件疲劳破坏的长寿命区；双对数多折线模型和三参数幂函数模型虽适用于构件疲劳破坏的中、长寿命区，但表达形式复杂，使用不便。本文拟结合各模型的优点，建立适用于构件疲劳破坏全寿命区的双对数双折线S—N曲线。

S—N曲线通常通过标准试件的疲劳试验得到。目前，疲劳试验存在多种试验方法，在传统的疲劳试验中常采用成组试验法，即在某一指定应力(或应变)水平下根据1组试样的多个试验结果测定构件的疲劳寿命，由此得到构件的S—N曲线。此法一般适用于构件疲劳破坏的中、短寿命区，但所需试验样本较多，试验成本高。为尽量降低试验成本，本文以闪光对焊连接的直径为16 mm的HRB400高强钢筋为例，采用单点试验法进行疲劳试验，合理控制试验样本数量，研究在小样本数据空间下能够用于构件疲劳破坏全寿命区的S—N曲线计算方法。

1　疲劳试验及结果

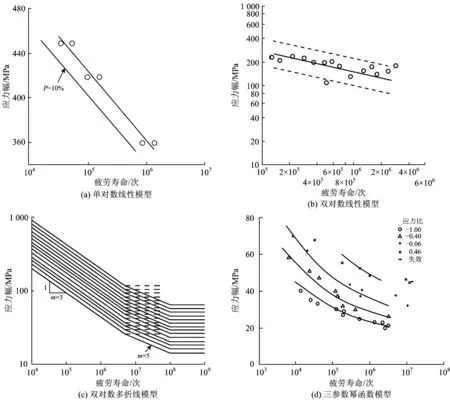
图1　S—N曲线模型

本文疲劳试验采用闪光对焊连接的直径16 mm的HRB400高强钢筋作为标准试件(以下简称试件)，其试验应力比取为0.2，试验加载的最大应力为320 MPa，是HRB400高强钢筋屈服强度的0.8倍。试验过程中加载应力依次降低，其中在试验的加载高应力区，加载应力约按5%的幅度依次降低，在试验的加载低应力区(接近疲劳极限时)，为满足升降法要求，加载应力约按1%幅度进行升降[6]。考虑到目前在我国现行规范[7]中大多只研究构件的200万次疲劳寿命，而在实际工程中部分构件的疲劳寿命远高于此[8]，因此有必要对构件的中、长疲劳寿命进行重点研究。在常规疲劳试验中，一般规定在荷载作用107次时，试样不出现疲劳破坏则认为其可承受无限次荷载的循环作用[9]，为探索适用于疲劳破坏全寿命区的S—N曲线，本试验的疲劳荷载循环次数达到107次。

试验用试件由国家建筑钢材质量监督检验中心进行统一取样。闪光对焊由现场焊接工人按实际施工要求进行焊接，不对焊接接头进行任何后续加工，疲劳试验试件共计26根。试验用高频疲劳试验机为GPS350高频疲劳试验机，如图2所示。直径16 mm的闪光对焊连接HRB400高强钢筋标准试件的疲劳试验结果汇总见表1。

图2　高频疲劳试验系统

疲劳试验过程中，当试件在夹具内或距离夹具末端小于一倍钢筋直径范围内发生断裂时，该试验结果视为无效[3]。疲劳试验中有效试件25根，无效试件1根。试验的成功率较高，试验结果可靠，可用于试件疲劳破坏全寿命区S—N曲线的研究。

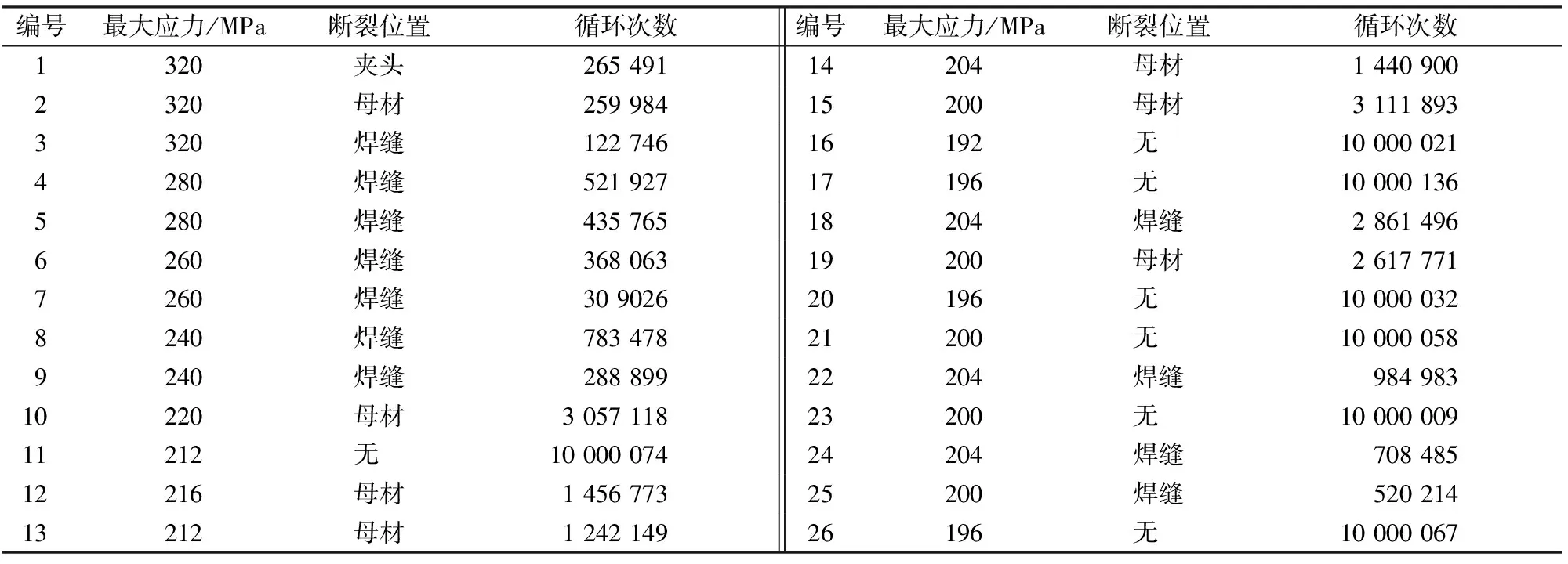
表1　疲劳试验结果

2　适用于疲劳全寿命区的双对数双折线S—N曲线的确定

本文提出的适用于疲劳破坏全寿命区的双对数双折线S—N曲线，其疲劳破坏中、短寿命区的S—N曲线采用斜率较大的线段表示(以下简称“第1段折线”)；而疲劳破坏长寿命区的S—N曲线采用斜率较小的线段表示(以下简称“第2段折线”)。

2.1　双对数双折线S—N曲线的第1段折线

2.1.1疲劳试验值的取舍

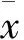
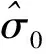
(1)

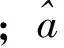
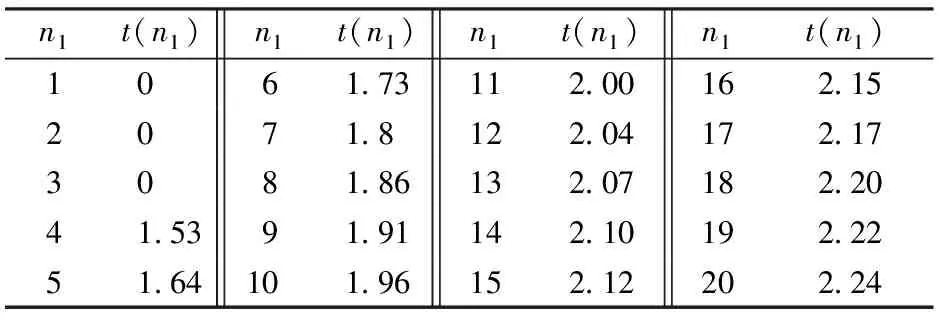
表2　t(n1)函数取值表

2.1.2基于一元线性回归的S—N曲线第1段折线求解

本文适用于构件疲劳破坏全寿命区的双对数双折线S—N曲线的第1段折线方程是基于一元线性回归原理确定的，以应力幅S为自变量，疲劳荷载循环次数N为因变量，即

x=a1+b1y

(2)

其中，y=lgS，x=lgN

式中：a1和b1为回归参数。

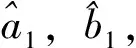
(3)

其中，

从表1的疲劳试验结果可以看出，编号为11的试件为首个疲劳荷载循环作用次数达到107次且未发生破坏的试件。由此，取该试件编号之前的试件(编号1—编号10)的试验数据作为双对数双折线S—N曲线第1段折线的原始数据点，排除其中无效的试验数据(在夹具内或距离夹具末端小于1倍该钢筋直径范围内破坏的试件的试验结果)后，采用改进的肖维奈准则进行筛选。基于一元线性回归原理，建立一元线性回归模型，得到：

x=14.94-3.98y

即lgN=14.94-3.98lgS

(4)

其中，相关系数R2=0.747。

2.2　双对数双折线S—N曲线的第2段折线

2.2.1基于升降法求解疲劳强度

当利用升降法求解试样的疲劳强度时，对被测各个试样按照其试验加载的最大应力值由小到大顺序排序，即S1≤S2≤…≤Sn3，相邻应力水平的失效与未失效试件组成升降法配对子。对疲劳强度的统计分析按正态分布估计参数，即

(5)

其中，

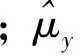
2.2.2基于三参数幂函数的S—N曲线第2段折线求解

在构件的疲劳破坏中、长寿命区，由于其疲劳寿命和应力幅已逐渐呈非线性关系，因此本文采用三参数幂函数模型以更能准确地描述该特性，其模型为

N(S-S0)β=α

(6)

式中：S0为三参数幂函数模型中的拟合疲劳极限强度；α，β均为待定系数。

根据文献[11]：对式(6)两边取对数得lgN+βlg(S-S0)=lgα， 取X=lgN，Y=lg(S-S0)，l=lgα,m=-β，则X=l+mY。由此变量X和Y之间呈线性关系，可以根据1组疲劳试验数据(Ni,Si)，i=1,2,…,n，通过式X=lgN,Y=lg(S-S0)求得相应的1组数据(Xi,Yi)，i=1,2,…,n，再由线性回归分析确定出待定参数l，m和相关系数R2。由此可以确定三参数幂函数模型的曲线方程。曲线方程确定后，其上任一点的切线斜率即可得到，具体为对式(6)进行求导，经过一系列化简可得

(7)

首先，基于升降法得到标准试件对应107次疲劳荷载循环作用的疲劳强度，本文将此值作为该类试件材料的疲劳极限强度。然后，根据其三参数幂函数S—N曲线方程，确定对应107次疲劳荷载循环作用时的三参数常函数曲线方程上对应点的切线斜率。由此知该直线斜率和直线过某一定点，则该直线方程唯一确定，此即为双对数双折线S—N曲线的第2段折线方程。

本文取编号1—编号10试件的试验数据为确定双对数双折线S—N曲线第1段折线的原始数据，则其余试验数据(编号11—编号26)为确定双对数双折线S—N曲线第2段折线的原始数据。由确定第2段折线的原始数据可知，有9个试样发生疲劳破坏，7个试样未发生疲劳破坏，用其中未发生破坏的试件试验数据与各相邻的发生疲劳破坏的试件试验数据组成1对升降法配对子，共计组成8个配对子，见表3(表中相邻的X和O组成1个配对子)。升降法共计6个应力水平，S1=192 MPa，应力台阶d=4 MPa。

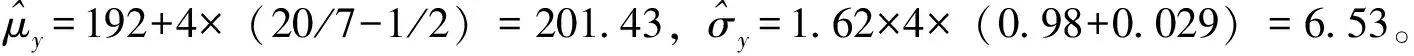
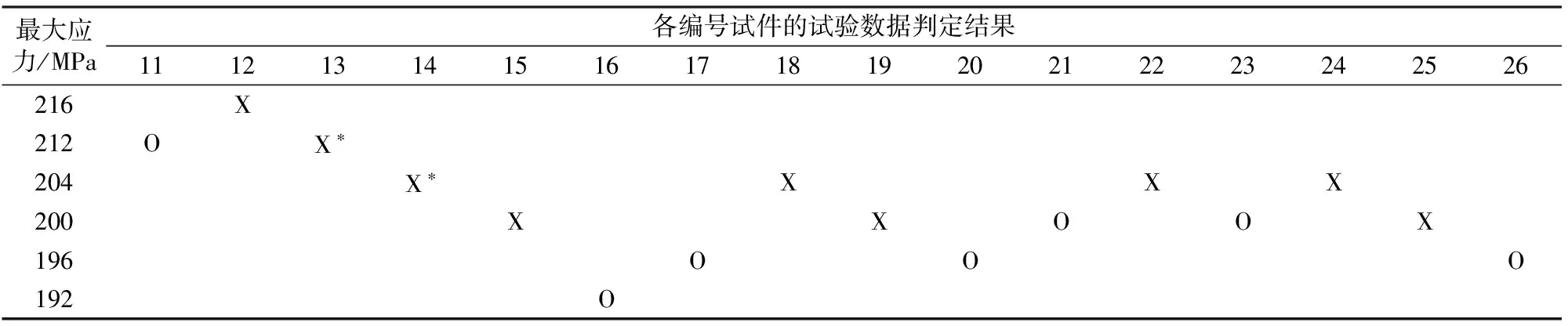
表3　升降法配对表

注：X表示发生疲劳破坏，O表示未发生疲劳破坏，X*表示未参与计算。

x=77.02-31.73y

即lgN=77.02-31.73lgS

(8)

2.3　适用于疲劳全寿命区的双对数双折线S—N曲线方程

联立上述双对数双折线S—N曲线的第1段折线方程式(4)和第2段折线方程式(8)，得到适用于疲劳全寿命区的双对数双折线S—N曲线，即为由式(4)和式(8)组成的分段函数，其分段点即为两段折线方程的交点(x0,y0)。综上，基于小样本空间的适用于试件的全寿命区S—N曲线方程为

(9)

式中：N0=10x0

进而可得到

(10)

由式(10)得到的应力比为0.2的试件全寿命区双对数双折线S—N曲线，如图3所示。

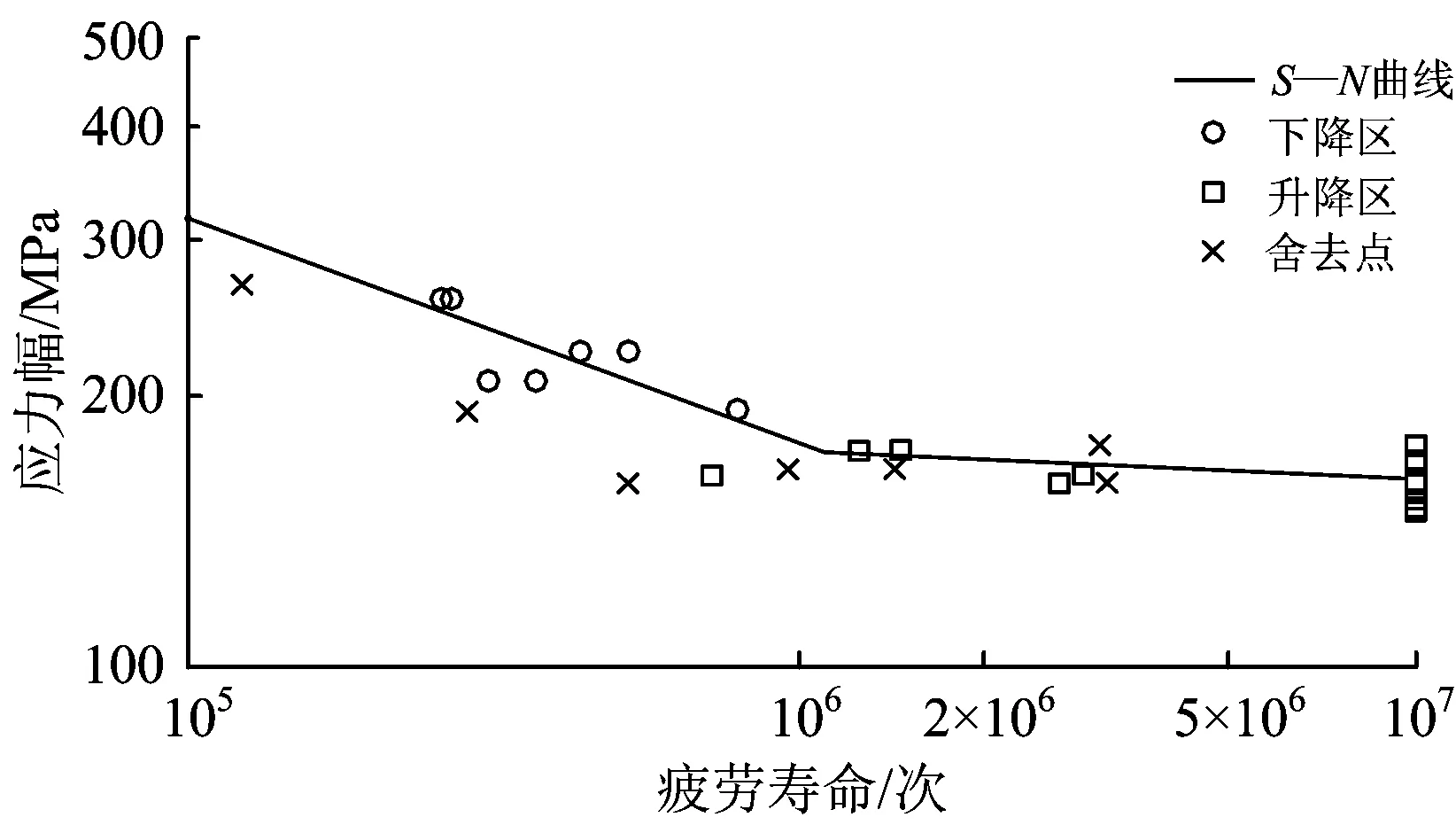
图3　双对数双折线S—N曲线

3　适用于疲劳全寿命区的双对数双折线S—N曲线可靠性分析

引入置信度和可靠度对上述双对数双折线S—N曲线进行分析。置信度是指总体参数值落在样本统计值某一区间内的概率[2]，本文用γ表示；可靠度(即存活率)是指1个零件(系统)在规定的环境和工作条件下，在试验标准期间完成用户期望功能的概率[12]，本文用P表示。

3.1　第1段折线可靠性分析

大量研究表明[1-2,10]，疲劳寿命服从正态分布。正态分布的表达式为

(11)

式中：μ为平均值，σ2为方差。

正态分布母体中样本可靠度(存活率)P的表达式为

(12)

其中，xp=μ+upσ

式中：xp为对应存活率P的百分位值，代表疲劳安全强度；up为与可靠度相关的标准正态偏量，可参见正态分布函数表。

百分位值xp可由样本的估计量确定

(13)

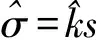
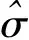
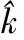
表4　标准差修正系数取值表

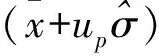
在给定置信度γ和可靠度P的条件下，与置信度相关的标准正态偏量μγ和与可靠度相关的标准正态偏量μp可分别由正态分布函数表查得，由此根据μγ和μp以及试验观测值数量n，可求出单侧容限系数f，f的近似公式为[1]

(14)

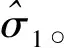
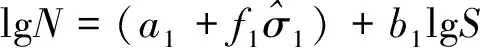
(15)

3.2　第2段折线可靠性分析

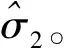
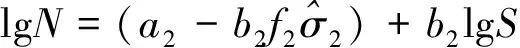
(16)

3.3　双对数双折线S—N曲线可靠性分析

本文取可靠度P=97.7%，置信度γ=95%进行分析，其表示形式为P97.7γ95。则根据式(15)和式(16)可得具有P97.7γ95的适用于构件疲劳破坏全寿命区的双对数双折线S—N曲线为

(17)

其中，N0,P97.7γ95=10x0,P97.7γ95。

上述双对数双折线S—N曲线第1段折线和第2段折线的交点为(x0,P97.7γ95,y0,P97.7γ95)，具体为

(18)

将式(18)代入式(17)，进而有

(19)

由式(19)得到P97.7γ95时应力比为0.2、直径为16 mm的闪光对焊连接HRB400高强钢筋在全寿命区的双对数双折线S—N曲线，如图4所示。

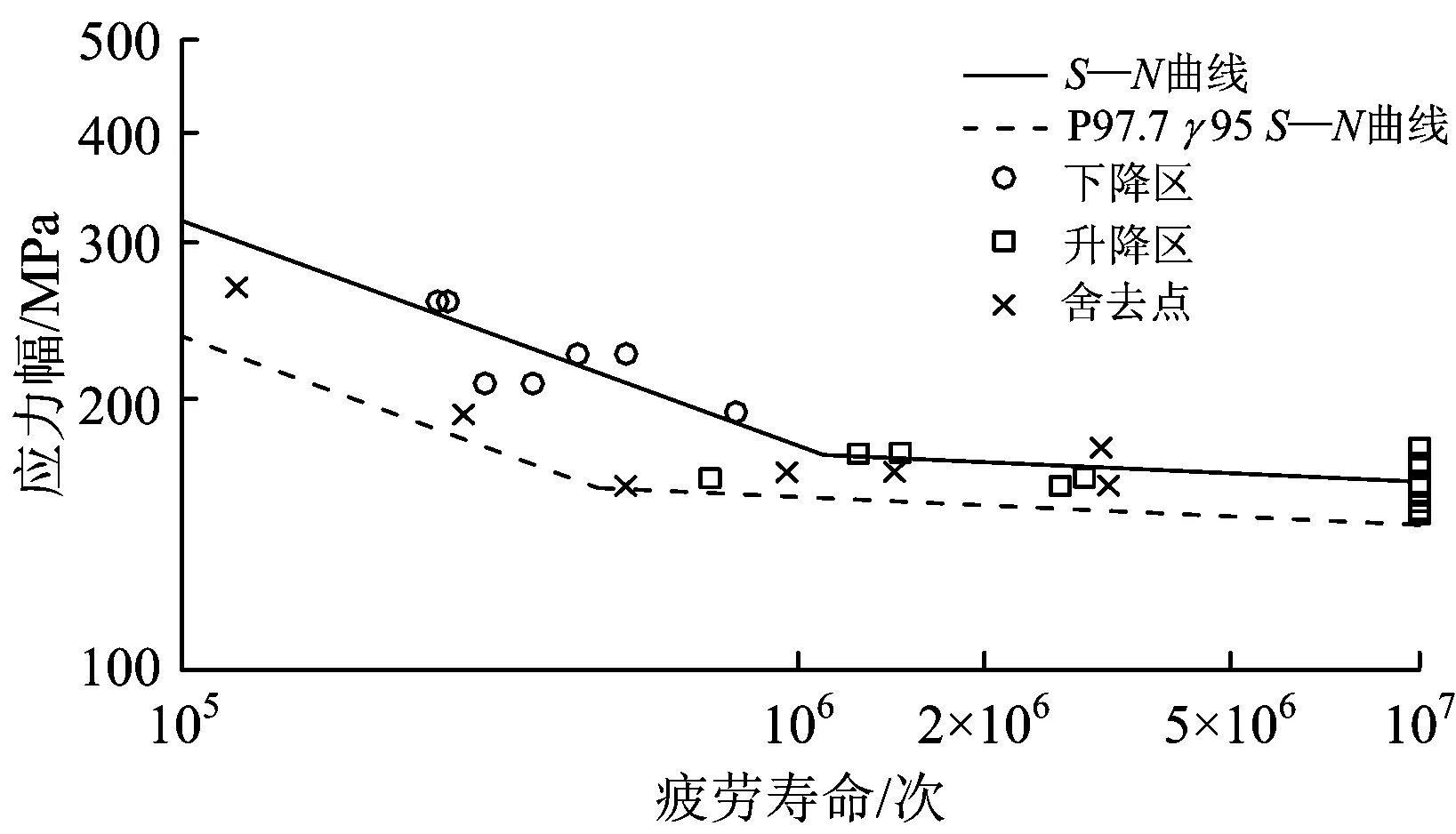
图4　考虑P97.7γ95时双对数双折线模型S—N曲线

4　结　语

本文结合常见S—N曲线的优点，提出1种适用于构件疲劳破坏全寿命区的双对数双折线S—N曲线，并研究在考虑置信度和可靠度时适用于构件疲劳破坏全寿命区的双对数双折线S—N曲线的求解方法。采用单点试验法对闪光对焊连接的HRB400高强钢筋试件进行高周疲劳试验，得到系列小样本试验数据，在此基础上，给出可疑试验值的取舍方法，提出“改进的肖维奈准则”并用于不同试验条件下可疑试验值的取舍判断。在给定可靠度P=97.7%和置信度γ=95%的情况下，给出了应力比为0.2、直径为16 mm的闪光对焊连接的HRB400高强钢筋试件的全寿命区双对数双折线S—N曲线。

[1]高镇同.疲劳应用统计学[M].北京:国防工业出版社,1986.

(GAO Zhentong. Fatigue Applied Statistics[M]. Beijing: National Defense Industry Press,1986. in Chinese)

[2]中华人民共和国国家质量监督检验检疫总局.GB/T 24176—2009 金属材料疲劳试验数据统计方案与分析方法[S].北京:中国标准出版社,2009.

(General Administration of Quality Supervision,Inspection and Quarantine of the People’s Republic of China. GB/T 24176—2009. Metallic Materials—Fatigue Testing—Statistical Planning and Analysis of Data[S]. Beijing: Standards Press of China,2009. in Chinese)

[3]中华人民共和国住房和城乡建设部.JGJT 27—2014 钢筋焊接接头试验方法标准[S]. 北京:中国建筑工业出版社,2014.

(Ministry of Housing and Urban-Rural Development of the People’s Republic of China. JGJT 27—2014 Standard for Test Methods of Welded Joint of Reinforcing Steel Bars[S]. Beijing: China Architecture & Building Press, 2014. in Chinese)

[4]British Standards Institution. BS—EN 1993—1—9:2005 Design of Steel Structures—Part 1—9: Fatigue[S]. London: the Standards Policy and Strategy Committee, 2005.

[5]Department of Defense and the Federal Aviation Administration. MIL-HDBK-5J Metallic Materials and Elements for Aerospace Vehicle Structures[S]. Virginia: Defense Standardization Program Office, 2003.

[6]中国铁路总公司.铁路工程应用高强钢筋试验[R].北京:中铁工程设计咨询集团有限公司,2014:80-90.

(China Railway Corporation. The Experimental Study on High-Strength Steel Bar Applied in Railway Engineering[R]. Beijing: China Railway Engineering Consulting Group Company Limited, 2014:80-90. in Chinese)

[7]中华人民共和国住房和城乡建设部. GB 50010—2010 混凝土结构设计规范[S].北京:中国建筑工业出版社,2010.

(Ministry of Housing and Urban-Rural Development of the People’s Republic of China. GB 50010—2010 Code for Design of Concrete Structures[S]. Beijing: China Architecture & Building Press, 2010. in Chinese)

[8]闫桂玲，王弘，康国政，等. 高速列车用6065A铝合金超高周疲劳性能试验研究[J].中国铁道科学,2014,35(1) :67-72.

(YAN Guiling，WAND Hong，KANG Guozheng，et al. Experimental Study on the Very High Cycle Fatigue Properties of 6065A Aluminum Alloy for High Speed Train[J].China Railway Science,2014,35(1):67-72. in Chinese)

[9]闫桂玲，王弘，高庆. 超声频率加载下50#车轴钢超长寿命疲劳性能研究[J].中国铁道科学,2004,25(2):78-81.

(YAN Guiling, WANG Hong, GAO Qing. On Ultra-long Life Fatigue Behavior of 50# Axle Steel under Ultrasonic Frequency[J].China Railway Science,2004,25(2) :78-81. in Chinese)

[10]高镇同，蒋新桐，熊峻江，等.疲劳性能试验设计和数据处理[M].北京:北京航空航天大学出版社,1999:15-20.

(GAO Zhentong, JIANG Xintong, XIONG Junjiang, et al. Experimental Design of Fatigue Property and Data Processing[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 1999:15-20. in Chinese)

[11]傅惠民，高镇同，梁美训. P-S—N曲线拟合法[J].航空学报,1988,9(7):338-341.

(FU Huimin, GAO Zhentong, LIANG Meixun. A Method for Fitting P-S—NCurve[J]. Acta Aeronautica et Astronautica Sinica,1988,9(7):338-341. in Chinese)

[12]LEE Yungli, PAN Jwo, HATHAWAY Richard, et al. Fatigue Testing and Analysis Theory and Practice[M]. Beijing: National Defense Industry Press, 2011:259-266.