高速铁路合分修隧道合分修长度的计算方法与参数优化
2017-04-10杨新安江星宏梁志辉肖粤秀
杨新安,江星宏,梁志辉,肖粤秀
(1.同济大学 交通运输工程学院,上海 201804;2.同济大学 道路与交通工程教育部重点实验室,上海 201804;3.招商局 重庆交通科研设计院有限公司,重庆 400067)
普通铁路隧道中含合分修结构形式的隧道被称为燕尾式隧道;公路隧道中含合分修结构形式的隧道被称为分岔隧道;高速铁路隧道中含合分修结构形式的隧道被称为合分修隧道。高速铁路合分修隧道与燕尾式隧道和分岔隧道相比,具有转弯半径大、占地面积小、空间利用率高、与大桥连接方便、进出隧道容易等优点,在适应地形、保护环境、控制工程量等方面效益突出。但是,合分修隧道的分岔角度小、开挖断面大、过渡曲线较长、断面多变、工序转换频繁,导致施工组织难度大,施工风险控制难,且已有的工程经验不多,更未有专门指导高速铁路合分修隧道合分修长度计算的理论。因此需要对高速铁路合分修隧道合分修长度进行深入研究。
目前,《高速铁路设计规范》[1]根据线型的平顺性、旅客的舒适性和设计速度,规定了平面曲线半径选取范围,确定了两相邻曲线间夹直线和曲线间圆曲线的最小长度。《铁路隧道设计规范》[2]规定隧道内的线路设计为曲线时,宜采用较大曲线半径,慎用较小曲线半径,并宜将曲线设在洞口附近。有些学者[3-7]采用数值模拟、监控量测或模型实验的方法,从开挖工法选择、施工力学特性、支护受力状态的角度对高速铁路合分修隧道进行了研究,但未从高速铁路合分修隧道线间距变化的角度研究过渡曲线的里程与线间距的关系。
秦方方[8]依据逆向工程中曲线重构理论,分析三次样条曲线拟合铁路既有曲线平面线形时所产生拟合误差的组成及其影响因素,提出1种既有曲线整正方法,可获得既有曲线上任意点的拨距量,该方法适用于偏角法和坐标法测量,可应用于非提速和提速线路的大中修。朱文升[9]论述了4-3-4型与英、法、德三国高速铁路所采用的3次改善型缓和曲线理论的主要特征及其差异,建议以4-3-4型作为我国高速铁路缓和曲线主选线型。李向国[10]针对三次抛物线型和半波正弦型2种线型的铁路缓和曲线,通过理论计算并与仿真计算结果进行对比,认为半波正弦型缓和曲线对提高旅客乘坐舒适度比三次抛物线型缓和曲线更具有优势。谢天辅[11]推导了1种新型非线性超高缓和曲线(6-3-6曲线),改进列车进入与驶出缓和曲线的动力性能。陈艾平[12]研究了我国时速160 km铁路最小曲线半径与缓和曲线的设计原则和标准,提出采用三次抛物线形缓和曲线是能满足运行要求的,采用半波正弦形缓和曲线能创造更好的运行条件。虽然这些学者考虑了平面曲线的线型特性,提出了平面曲线设计理论,但是并没有提出合分修长度的计算理论,也没有研究合分修长度与过渡曲线参数之间的关系。
综上所述,高速铁路合分修隧道过渡曲线参数是根据《高速铁路设计规范》进行取值的,但规范中没有给出高速铁路合分修隧道过渡曲线线间距变化过程中合分修长度的计算理论。因此,本文基于《高速铁路设计规范》,针对高速铁路合分修隧道过渡曲线2种线型,分别建立直角坐标系,根据曲线和方程理论,推导在过渡曲线里程范围内过渡曲线上任意一点的线间距与其里程的函数表达式,在此基础上给出合分修长度的计算方法,并分析合分修长度与过渡曲线参数之间的关系;通过工程案例验证合分修长度计算方法的有效性和合理性,为指导高速铁路合分修隧道合分修段曲线参数的设计优化提供理论依据。
1 合分修长度计算方法
高速铁路合分修隧道过渡曲线中合分修长度是指合分修起、止点间的距离,因过渡曲线的转角较小,所以合分修长度约等于合分修段在x轴上的投影距离。在高速铁路合分修隧道过渡开始处,过渡曲线的线间距为0,里程为0;随着里程的增加,过渡曲线的线间距增大;在过渡结束处,过渡曲线两线平行,线间距达到最大值(即高速铁路线路设计线间距)。因此,在高速铁路合分修隧道线间距变化过程中,在一定的过渡曲线里程范围内,依据曲线和方程理论,推导过渡曲线上任意一点的线间距y与其里程x的函数关系式, 即y=F(x),在此基础上给出合分修长度的计算方法。
1.1 过渡曲线线型
高速铁路合分修隧道过渡曲线根据过渡曲线线间距加宽起点所在曲线形式的不同分为2种:当所在曲线是直线时为Ⅰ类过渡曲线;当所在曲线是圆曲线时为Ⅱ类过渡曲线[13]。对这2类过渡曲线分别建立直角坐标系,如图1所示。图1中:Ⅰ类过渡曲线以左线直缓点ZHL为原点、直线延长方向为x轴、缓和曲线曲率半径方向为y轴建立直角坐标系,Ⅰ类过渡曲线的里程范围是指自左线直缓点ZHL起至左线圆缓点YHL止的区间;Ⅱ类过渡曲线以右线圆缓点YHR为原点、圆曲线切向为x轴、线间距加大方向为正、圆曲线径向为y轴建立直角坐标系,Ⅱ类过渡曲线的里程范围是指自右线圆缓点YHR起至右线缓圆点HYR止的区间;R1为左线圆曲线半径,R2为右线圆曲线半径;d和α分别为合分修结束时的线间距和线路转角;Z表示直线,H表示缓和曲线,Y表示圆曲线,下角标L和R分别表示左线、右线。Ⅰ类过渡曲线左、右线的线型相同,均为直线—缓和曲线—圆曲线—缓和曲线—直线;Ⅱ类过渡曲线左、右线的线型不同,左线为圆曲线—缓和曲线—直线,右线为圆曲线—缓和曲线—直线—缓和曲线—圆曲线—缓和曲线—直线。
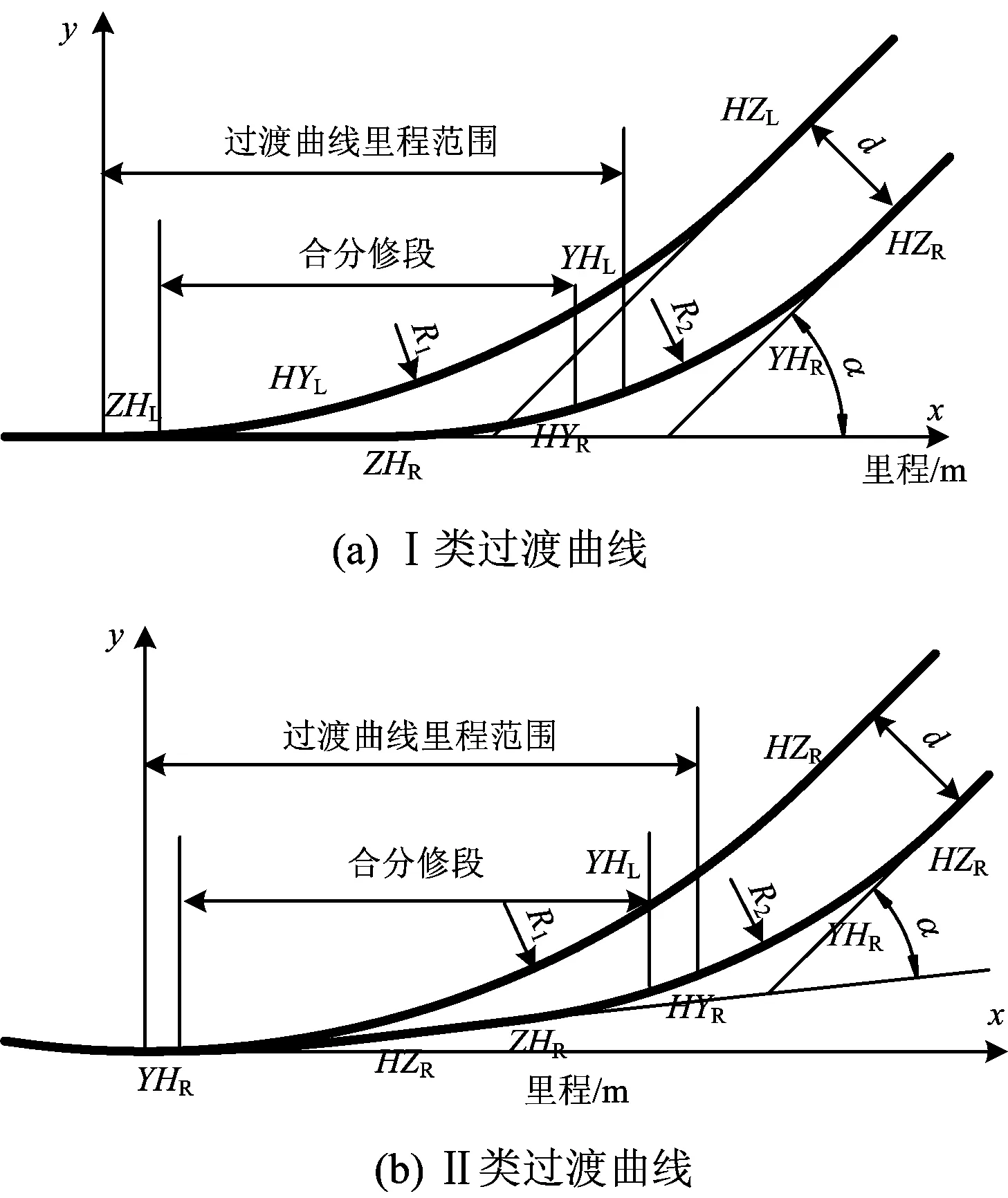
图1 合分修隧道过渡曲线线型示意图
1.2 Ⅰ类过渡曲线线间距的函数表达式
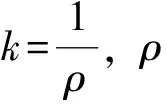
1)左线的曲线方程
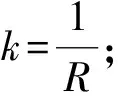
(1)
(2)
式中:C为积分常数。
对于直缓点ZH,有l=0,φ=0;将其代入式(2),可得C=0;则式(2)可以简化为
(3)
Ⅰ类过渡曲线左线缓和曲线方程计算示意图如图2所示。
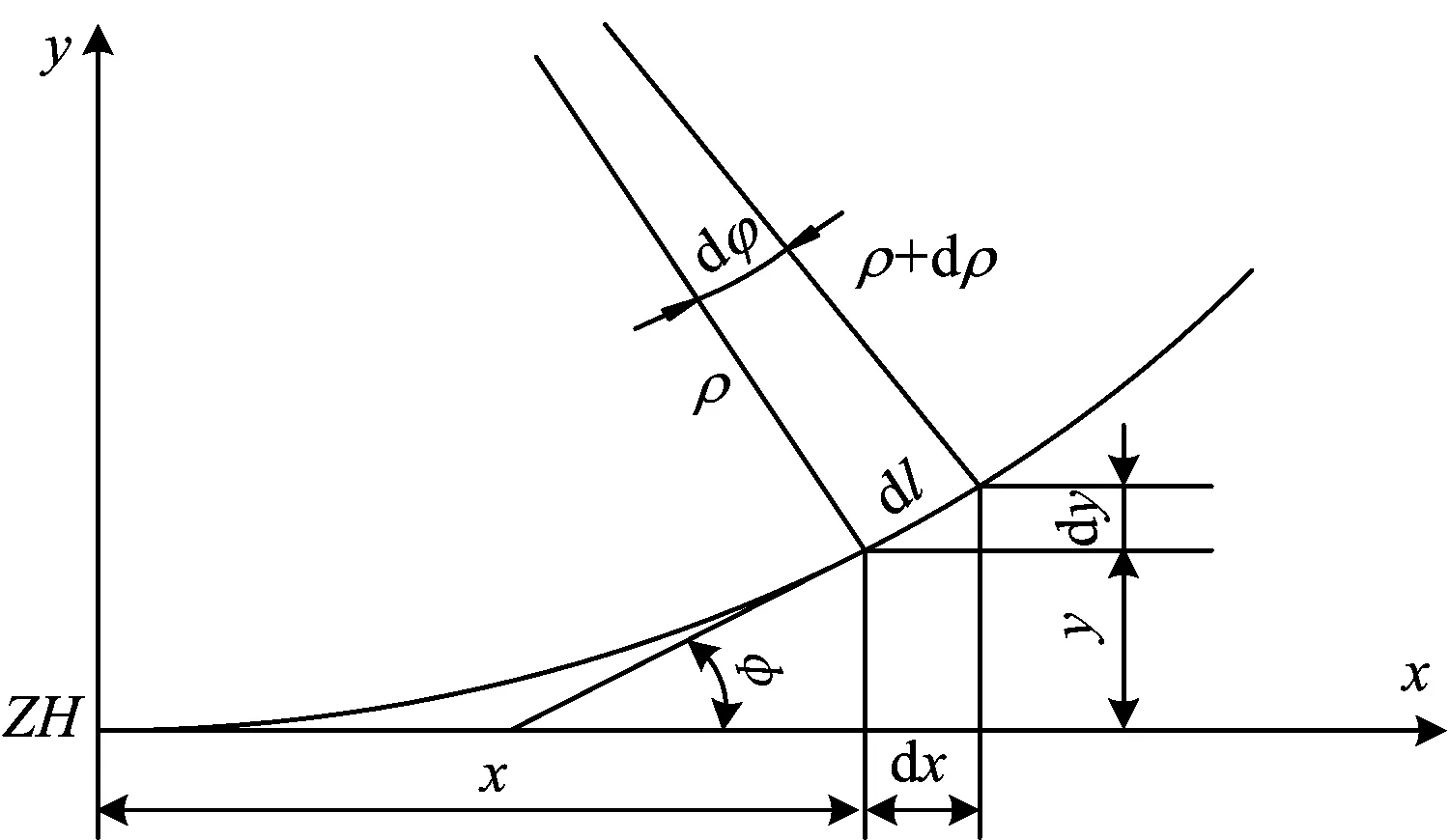
图2 左线缓和曲线方程计算示意图
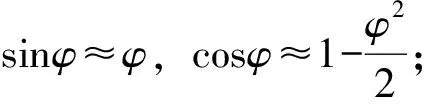
(4)
由于x的方程第2项的数值甚小,可以忽略,则有x≈l0。因而,Ⅰ类过渡曲线左线缓和曲线方程为
(5)
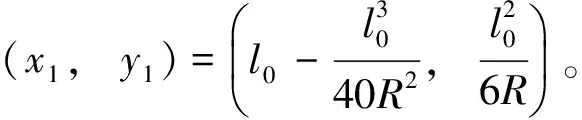
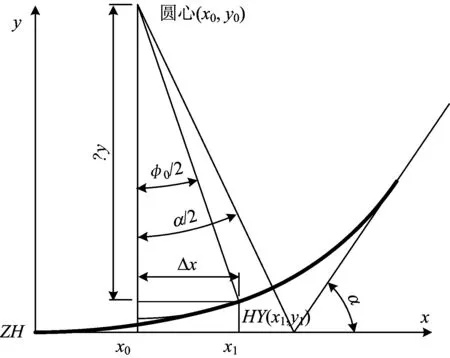
图3 左线圆曲线方程计算示意图
根据图3中的几何关系可知,圆曲线圆心坐标与缓圆点HYL坐标的关系为(x0,y0)=(x1-Δx,y1+Δy)。
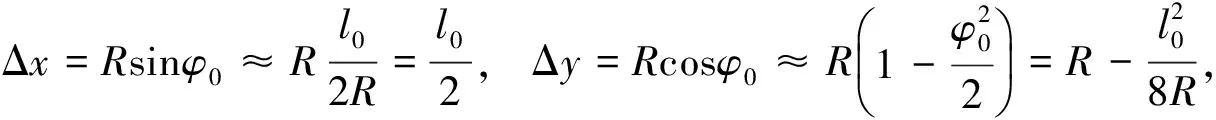
(6)
因为由圆心坐标和半径表示的圆曲线方程为
(x-x0)2+(y0-y)2=R2
(7)
将式(6)代入式(7)求解可得圆曲线方程为
(8)
联立式(5)和式(8)可得Ⅰ类过渡曲线左线的曲线方程为
(9)
2)右线的曲线方程
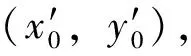
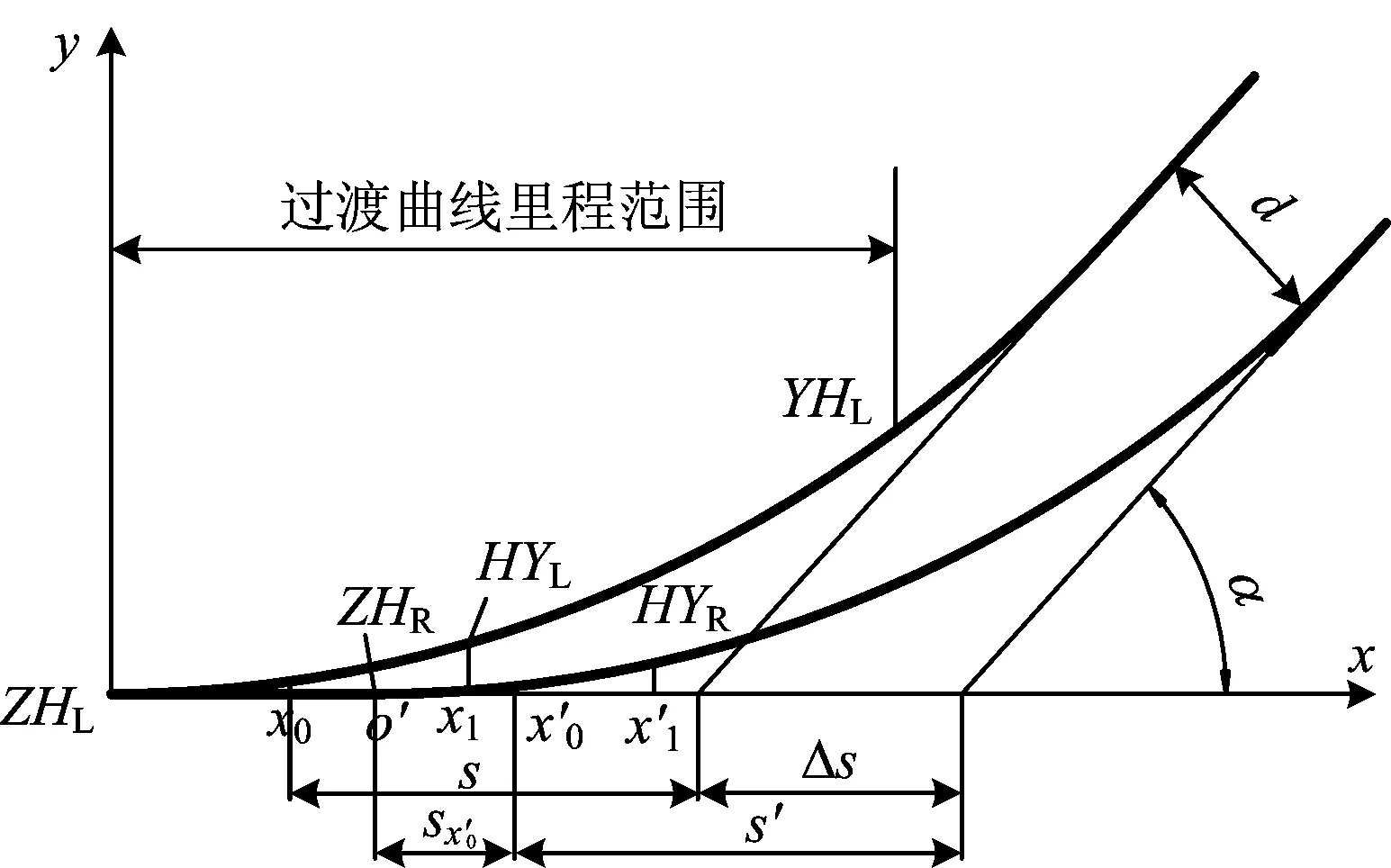
图4 Ⅰ类过渡曲线右线关键点位置关系图
由图4可知,右线直缓点ZHR的x坐标为
(10)
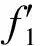
综上,Ⅰ类过渡曲线右线的曲线方程为
(11)
3)过渡曲线线间距的函数表达式
高速铁路合分修隧道的线路转角较小,合分修距离较长,可近似认为过渡曲线左、右线的线间距等于左、右线两曲线纵坐标的差值,因此,由式(9)和式(11)可得过渡曲线线间距的函数表达式。
当o′≥x1时,高速铁路合分修隧道Ⅰ类过渡曲线线间距的函数表达式为
y=F(x)=
(12)
当o′ (13) 1)左线的曲线方程 Ⅱ类过渡曲线左线圆曲线的圆心坐标(x0,y0)=(0,R),代入式(8)可得左线圆曲线的方程为 (14) 2)右线的曲线方程 (15) 对式(15)积分可得 (16) 式中:C1和C2为积分常数。 因此,右线缓和曲线的方程为 (17) (18) 联立式(17)和式(18)可得Ⅱ类过渡曲线右线的曲线方程为 (19) 3)过渡曲线线间距的函数表达式 同理,联立式(14)和式(19)可得高速铁路合分修隧道Ⅱ类过渡曲线线间距的函数表达示为 (20) 反算式(12),或者式(13),或者式(20),在过渡曲线里程范围内,可求得里程x与线间距y的关系为 x=F-1(y) (21) 已知合分修开始时的线间距yb和结束时的线间距ye,采用式(21)可求得对应合分修的起始里程xb和终止里程xe,因此合分修长度L可表示为 L=xe-xb=F-1(ye)-F-1(yb) (22) 根据《高速铁路设计规范》,线间距d取8.31 m,过渡曲线转角α取5°~15°;圆曲线半径R及缓和曲线长度l0的取值见表1。 表1 圆曲线半径与缓和曲线长度的对应取值 比照实际合分修隧道,当线路转角α为6.5°时,采用式(22)计算Ⅰ类过渡曲线不同内、外侧圆曲线半径时的合分修长度,结果如图5所示。由图5(a)可知:在内侧圆曲线半径为12 000 m的条件下,合分修长度随外侧圆曲线半径的增大而增大;当外侧圆曲线半径大于10 000 m时,外侧圆曲线半径对合分修长度的影响极大。由图5(b)可知:在外侧圆曲线半径为7 000 m时,合分修长度随内侧圆曲线半径的增大而减小;当内侧圆曲线半径小于9 000 m时,合分修长度随内侧圆曲线半径的减小而大幅上升。因此,对于Ⅰ类过渡曲线,选择圆曲线半径时,外侧宜小,且不应大于10 000 m;内侧宜大,且不应小于9 000 m。 图5 合分修长度与内外侧圆曲线半径的关系 在不同内外侧圆曲线半径条件下,合分修长度与线路转角α的关系见表2,由表2可得如下结论。 表2 不同内外侧圆曲线半径条件下合分修长度与线路转角的关系表 (1)当内外侧圆曲线半径相等时,合分修长度随线路转角的增加而大幅上升,说明此时应优先考虑较小的线路转角。 (2)当内外侧圆曲线半径差值为1 000 m时,合分修长度随线路转角的增大而增大,当线路转角增大到11°时,合分修长度趋于稳定,说明此时应优先考虑较小的线路转角。 (3)在内外侧圆曲线半径差为2 000 m条件下,当线路转角小于9°时,合分修长度随线路转角的增大而增大,当线路转角大于9°时,合分修长度随线路转角的增大而减小,说明此时应优先考虑较大的线路转角。 (4)在内外侧圆曲线半径差值为3 000 m条件下,当线路转角小于8°时,合分修长度随线路转角的增大而增大,当线路转角大于8°时,合分修长度随线路转角的增大而减小,说明此时应优先考虑较大的线路转角。 (5)在内外侧圆曲线半径差值为4 000 m条件下,当线路转角小于7°时,合分修长度随线路转角的增大而增大,当线路转角大于7°,合分修长度随线路转角的增大而减小,说明此时应优先考虑较大的线路转角。 (6)在内外侧圆曲线半径差值为5 000 m条件下,当线路转角小于6°时,合分修长度随线路转角的增大而增大,当线路转角大于6°时,合分修长度随线路转角的增大而减小,说明此时应优先考虑较大的线路转角。 由上可知,对于Ⅰ类过渡曲线条件下,应避免内外侧曲线采用相近的圆曲线半径,线路转角不宜选取9°~12°。 由Ⅱ类过渡曲线线间距的函数表达式(20)的推导过程可知,式 (20)中不含变量线路转角α,因此,线路转角α对Ⅱ类过渡曲线合分修长度没有影响。采用式(22)计算Ⅱ类过渡曲线合分修长度与圆曲线半径的关系,结果见表3。由表3可知:在不同圆曲线半径条件下,合分修长度均在440 m左右,极差仅为7 m,说明Ⅱ类过渡曲线合分修长度也不受圆曲线半径的影响。由此可知,采用Ⅱ类合分修过渡曲线时的合分修长度为440±3 m,且合分修长度受过渡曲线参数取值影响程度小。对比表2和表3可知:采用Ⅱ类过渡曲线时,合分修长度比采用Ⅰ类过渡曲线时要短。 表3 Ⅱ类过渡曲线合分修长度与圆曲线半径的关系 m 凤凰山隧道合分修段洞身围岩主要通过二叠系上统峨眉山组玄武岩夹凝灰岩(P2β)及下统茅口组灰岩(P1m),地质构造较复杂,区域性逆断层发育。灰岩与玄武岩夹凝灰岩过渡段,岩体破碎,易塌方、冒顶;茅口组灰岩段,易突水突泥。工程地质条件较差,施工风险大,控制难度高,围岩等级为Ⅴ级。 凤凰山隧道合分修过渡曲线线型采用Ⅰ类过渡曲线,如图6所示,内侧圆曲线半径R1和外侧圆曲线半径R2均为12 000 m,线路转角α为6.5°;合分修起点的线间距yb=0.18 m,终点的线间距ye=8.31m。采用式(21)计算得到合分修起点的里程为xb=175 m,终点的里程xe=761m;采用式(22)计算得到合分修长度为L=xe-xb=586 m。实际现场中合分修长度为585 m,可见两者相差极小,验证了本文提出的Ⅰ类过渡曲线合分修长度计算方法是正确和有效的。 图6 凤凰山隧道合分修示意图(单位:m) 表4 凤凰山隧道合分修长度与圆曲线半径的关系表 m 凤凰山隧道过渡曲线起点为直线,线路转角α=6.5°,合分修结束时线间距d=8.31 m。选择不同圆曲线半径时,采用本文提出的合分修长度计算方法计算的合分修长度见表4。由表4可知,合分修长度的最小值为469 m,最大值为586 m,两者相差117 m,说明合分修过渡曲线左线、右线的圆曲线半径均取12 000 m并非是最优方案,而左线圆曲线半径仍取12 000 m、右线圆曲线半径取7 000 m时优势较明显。 壁板坡隧道位于二叠系下统茅口组(P1m)厚层灰岩与二叠系下统栖霞组(P1q)中厚层灰岩过渡区域,岩性致密坚硬,弱风化,为Ⅴ级次坚石。区段内围岩节理裂隙发育程度低,地下水含量少,围岩条件好,大跨渐变段围岩等级为Ⅲ级,小间距段围岩等级为Ⅳ级。 合分修过渡曲线线型采用Ⅱ类过渡曲线,如图7所示,合分修起始点距隧道进口923 m。合分修起始点的线间距d=0.20 cm,结束点的线间距d=8.31 m,采用式(21)计算得到合分修起点的里程为xb=179 m,终点的里程为xe=619 m。采用式(22)计算得到合分修长度L=xe-xb=619-179=440 m,实际现场中合分修长度为440 m,可见两者相同,证明对于Ⅱ类过渡曲线,本文提出的合分修长度计算方法也是正确和有效的。 图7 壁板坡隧道合分修示意图(单位:m) (1)针对高速铁路合分修隧道的2种类型过渡曲线,推导得到这2种过渡曲线线间距的函数表达式;根据已知的合分修开始和结束时的线间距,反算线间距函数表达式,得到合分修开始和结束时的里程;再计算合分修开始和结束时里程之差,就得到合分修长度。依据合分修长度计算方法分析合分修长度与过渡曲线参数的关系。最后通过2个工程案例证明了提出的合分修长度计算方法的正确性和有效性。 (2)对于Ⅰ类过渡曲线,合分修长度受圆曲线半径R、线路转角α等因素的影响程度较大。为缩短合分修长度:内侧圆曲线半径宜大,不应小于9 000 m;外侧宜小,不应大于10 000 m;应避免内外侧曲线采用相近的圆曲线半径;线路转角不宜选取9°~12°。 (3) 对于Ⅱ类过渡曲线,合分修长度不受圆曲线半径R、线路转角α等因素的影响;且合分修长度比采用Ⅰ类过渡曲线时的合分修长度短。 (4)采用Ⅰ类过渡曲线时的合分修长度明显大于采用Ⅱ类过渡曲线时的合分修长度,但有利于降低合分修段的施工风险,因此建议线路过渡曲线设计中优先考虑Ⅰ类过渡曲线。 [1]铁道第三勘察设计院. TB 10621—2014高速铁路设计规范[S]. 北京: 中国铁道出版社, 2014. (The Third Railway Survey and Design Institute Group Corporation. TB 10621—2014 Code for Design of High Speed Railway [S]. Beijing: China Railway Publishing House,2014. in Chinese) [2]铁道第二勘察设计院. TB 10003—2005铁路隧道设计规范[S]. 北京: 中国铁道出版社,2005. (The Second Railway Survey and Design Institute Group Corporation. TB 10003—2005 Code for Design on Tunnel of Railway [S]. Beijing: China Railway Publishing House,2005. in Chinese) [3]张庆松, 李术才, 李利平. 分岔隧道大拱段围岩稳定性监控与爆破振动效应分析[J]. 岩石力学与工程学报,2008, 27(7): 1462-1468. (ZHANG Qingsong, LI Shucai,LI Liping. Study of Blasting Dynamic Effect and Site Monitoring of Large-Span Shallow Part of Bifurcated Tunnel [J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(7): 1462-1468. in Chinese) [4]吴波, 刘维宁, 高波, 等. 地铁分岔隧道施工性态的三维数值模拟与分析[J]. 岩石力学与工程学报, 2004, 23(18): 3081-3086. (WU Bo, LIU Weining, GAO Bo, et al. 3D Simulation and Analysis on Construction Behavior of Forked Metro Tunnel [J]. Chinese Journal of Rock Mechanics and Engineering,2004, 23(18): 3081-3086. in Chinese) [5]王者超, 李术才, 陈卫忠. 分岔隧道变形监测与施工对策研究[J]. 岩土力学,2007, 28(4): 785-789. (WANG Zhechao, LI Shucai, CHEN Weizhong. Deformation Monitoring of Bifurcation Tunnel and Countermeasures of Construction Technologies [J]. Rock and Soil Mechanics, 2007, 28(4): 785-789. in Chinese) [6]王汉鹏, 李术才, 张强勇. 分岔隧道模型试验与数值模拟超载安全度研究[J]. 岩土力学,2008, 29(9): 2521-2526. (WANG Hanpeng, LI Shucai, ZHANG Qiangyong. Model Test and Numerical Simulation of Overload Safety of Forked Tunnel [J]. Rock and Soil Mechanics, 2008, 29(9): 2521-2526. in Chinese) [7]王汉鹏. 分岔式隧道设计施工的关键技术研究[D]. 济南:山东大学, 2007. (WANG Hanpeng. Key Technology Study on Forked Tunnel Design and Construction [D]. Jinan:Shandong University, 2007. in Chinese) [8]秦方方, 易思蓉, 杨长根. 基于三次样条曲线的铁路既有曲线整正方法[J]. 中国铁道科学, 2010, 31(2): 18-23. (QIN Fangfang, YI Sirong, YANG Changgen. Method for the Realignment of the Existing Railway Curve Based on the Cubic Spline Curve [J]. China Railway Science, 2010, 31(2): 18-23. in Chinese) [9]朱文升. 4-3-4型与3次改善型缓和曲线理论上的主要特征及其差异[J]. 中国铁道科学, 1997, 18(2): 36-45. (ZHU Wensheng. The Main Features and the Differences between Transition Curves of 4-3-4 Shape and 3 Power Improved Shape [J]. China Railway Science, 1997, 18(2): 36-45. in Chinese) [10]李向国, 李木松, 卜建清,等. 2种铁路缓和曲线线型力学性能对比分析[J]. 中国铁道科学, 2009, 30(6): 1-6. (LI Xiangguo, LI Musong, BU Jianqing,et al. Comparative Analysis on the Linetype Mechanical Performances of Two Railway Transition Curves [J]. China Railway Science, 2009, 30(6): 1-6. in Chinese) [11]谢天辅, 刘锡臣. 6-3-6铁路缓和曲线与缓和曲线线型的讨论[J]. 中国铁道科学, 1984,5(1): 72-82. (XIE Tianfu, LIU Xichen. The 6-3-6 Transition Curve and Discussions on the Various Types of Transition Curve[J]. China Railway Science, 1984, 5(1): 72-82. in Chinese) [12]陈艾平, 宋鸣德, 朱文升. 时速160公里铁路最小曲线半径与缓和曲线设计标准的研究[J]. 中国铁道科学, 1985, 6(2): 14-32. (CHEN Aiping, SONG Mingde, ZHU Wensheng. Study on the Criteria for Minimum Radius of Curve and the Transition Curve for 160 km·h-1Railway Track [J]. China Railway Science, 1985, 6(2): 14-32. in Chinese) [13]江星宏. 高速铁路隧道合分修开挖特性与支护优化研究[D]. 上海:同济大学, 2016. (JIANG Xinghong. Study on Excavation Characteristics and Lining Optimization of High-Way Branched Tunnel[D]. Shanghai: Tongji University, 2016. in Chinese)1.3 Ⅱ类过渡曲线线间距的函数表达式
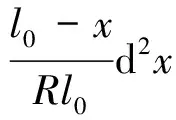
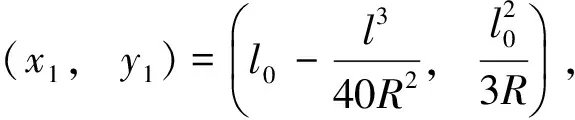
1.4 合分修长度计算方法
2 影响合分修长度的过渡曲线参数
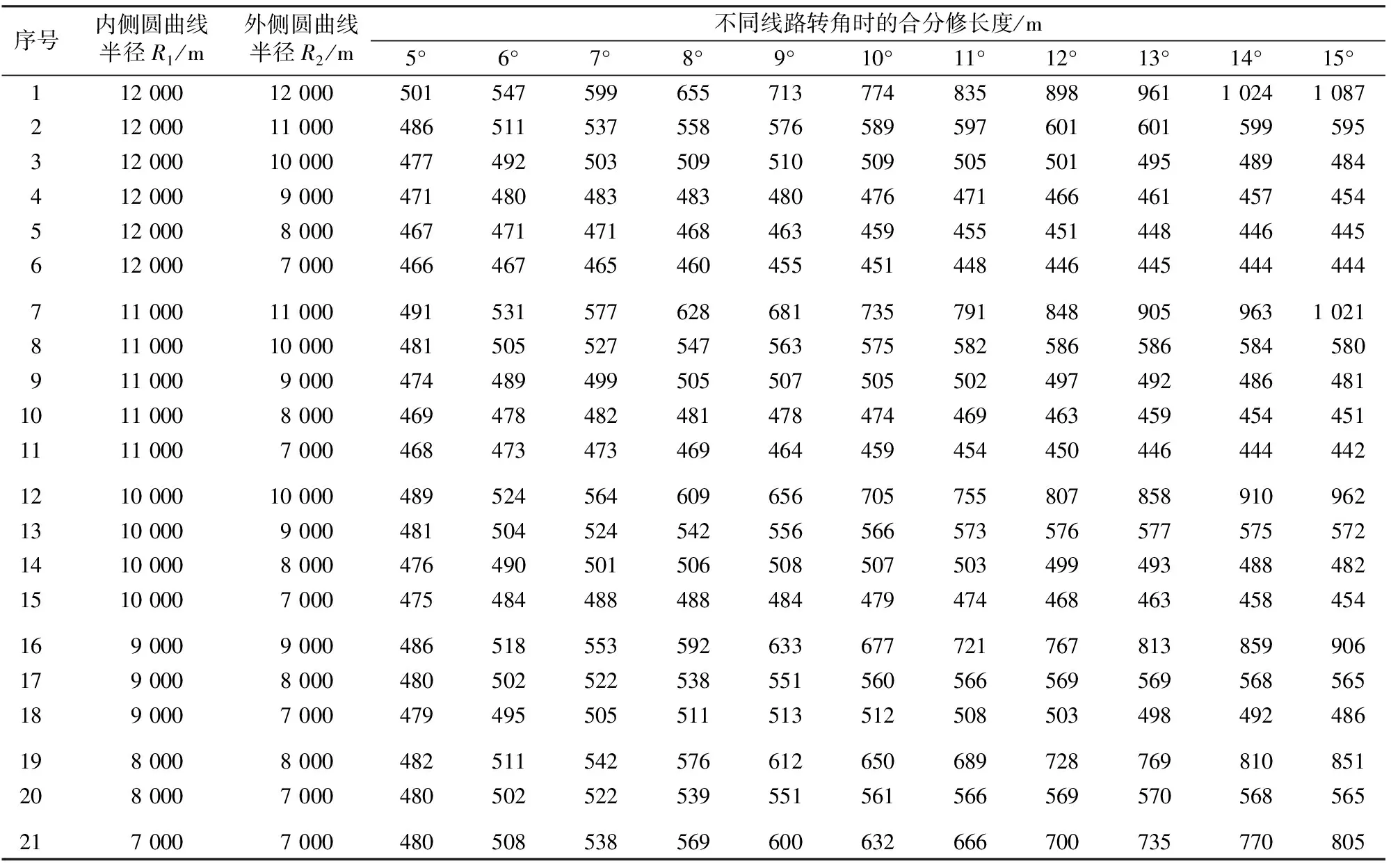
2.1 过渡曲线参数取值

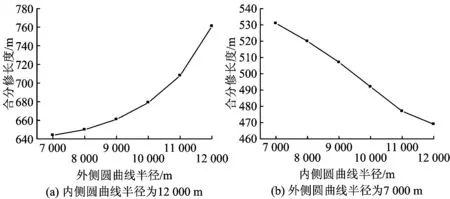
2.2 Ⅰ类过渡曲线参数
2.3 Ⅱ类过渡曲线参数
3 工程应用与实例
3.1 凤凰山隧道
3.2 壁板坡隧道
4 结 论
