基于彩虹表技术的分布式密码破解研究
2017-04-10王伟兵文伯聪
王伟兵, 文伯聪
(广东警官学院计算机系, 广东广州 510230)
基于彩虹表技术的分布式密码破解研究
王伟兵, 文伯聪
(广东警官学院计算机系, 广东广州 510230)
在打击计算机类型的犯罪过程中,为了获得侦查线索或者证明案情的电子证据,经常需要通过技术手段破解犯罪嫌疑人计算机中的各种密码。本文研究了彩虹表的基本原理以及常用操作系统的密码加密流程,提出了利用MPI分布式编程模型构造彩虹表以及基于彩虹表破解密码的方法。实验表明,这些方法是有效的,可以满足侦查实战的需要。
彩虹表; 密码破解; MPI; 电子取证; 分布式
0 引言
随着互联网的快速发展,利用计算机及其网络进行计算机犯罪的问题越来越严重。在这类案件的侦破过程中,为了获得侦查线索或者提取用于证明犯罪事实的电子证据,往往需要在犯罪嫌疑人的计算机中查看有关文件。在通过口供无法获得密码的情况下,登录涉案计算机或者打开涉案文件,是非常困难的。这种情况下,密码破解技术可能就成了唯一的选择。
无论是理论还是实践中,直接破解密码算法几乎是不可能的。所以通常情况下,破解密码往往采用穷举法或查表法。使用穷举法破解每一个密码时,都要遍历密码明文空间中的每一个密码,对每一个密码都要计算加密后的结果,然后和存储在计算机或文档中的密文进行对比。这种方法破解密码所需时间非常长,没有实用价值。而查表法刚好相反,先把密码明文空间中的所有密码的密文计算一遍,将计算结果以线性表的形式存储起来。密码破解时,以需要破解的密文为关键字,在预先计算并存储的线性表中查找比对。这种方式破解密码的速度比穷举法快,但是需要非常海量的存储空间,在实际办案工作中几乎没有这样的资源。而Hellman和Oechslin等人提出的时空折中算法(彩虹表法),则在破解时间和存储空间两个维度上折中,在满足破解速度要求的前提下,大大降低对存储空间的要求,因此是一种能满足实战需求的实用性方法。
本文在经典彩虹表的算法基础上,提出构造分布式完美彩虹表的思路,通过MPI并行编程接口,将彩虹表分布存储于集群中的每台计算机中。在破解阶段,通过集群中的多台计算机并行计算,可大大加快和提高密码破解的速度和有效率。
1 彩虹表算法分析
1.1 概念提出
无论是操作系统的登录密码,还是文档资料的打开密码,通常都是采用单向散列函数(Hash函数)处理后存储。在单向散列算法中,对于某个明文P(明文有N种可能性),使用单向散列函数H计算,得到固定长度的散列值C(密文),记作:
C=H(P)
采用查表法破解密码的过程是:首先遍历整个密码明文空间中的每个密码,对每个密码按照上述函数计算密文(散列值),然后将所有的密文排序并连同明文一起存储成一张线性表。破解密码时,首先要拿到该密码的密文,然后使用折半查找法在该线性表中查找比对,进而获得密码明文。这个过程中,查找比对次数不超过log2N,哈希计算次数为N,预先计算存储的线性表可重复使用。但是由于明文空间尺寸N非常巨大,这个预处理表的占用的存储空间将非常大。
Hellman在1980年提出采用时空折中的思想破解DES算法的密钥。Oechslin于2013年发表论文提出了对经典方法的改进,大大提高了密码破解的速度。改进后的方法称为彩虹表法。
彩虹表方法的核心思想是一系列简化函数(R1,R2,R3,…,Rk),每个简化函数的功能是将一个密文映射为明文空间中的一个密码。在彩虹表构造阶段,先从一个明文P0开始,计算哈希函数H(P0),得到密文C1后,再使用化简函数R1(C1),计算出另一明文P1,然后重复使用哈希函数H和简化函数R进行计算,就生成了一条密码明文与密文交替出现的链:
这种预计算出来的链结构就称为彩虹链,多条彩虹链组成的预计算表称之为彩虹表。
1.2 构造彩虹表
在彩虹表构造阶段,首先从密码的明文空间中随机选择s个明文{P1,0,P2,0,…,Ps,0}作为计算起点,然后按下列方式依次计算,形成s条彩虹链:
其中s和k是彩虹表方法的参数,不同的参数值决定了彩虹表的构造时间和所占存储空间,也决定了基于此彩虹表破解密码的时间。为了减少存储空间,不需要保存彩虹链中间各个结点,只存储每条彩虹链的链首和链尾组成的记录,并按链尾进行排序。
1.3 破解过程
彩虹表构造完成并存储后,就可依此表破解密码了。对于已知的某个密文C,想要找到对应的明文P,过程如下:
(1)首先使用简约函数Rk(C)计算出Pk,用Pk作为关键字在彩虹表中存储的所有链尾构成的线性表中进行折半查找,如果匹配到对应链尾,则从该彩虹链的链首重新计算整条彩虹链,计算出Ck后,比较Ck和C,如果相等则表明上一步的计算结果Pk-1就是密文C对应的明文,如果不相等,就称为一次误警。
(2)如果Pk在彩虹表中的所有链尾上折半查找不成功,则认为明文不可能出现在Pk-1的位置上。于是对密文C进行Rk-1(H(Rk-2(C)))函数运算,用计算结果在彩虹表中的所有链尾结点中进行二分查找。查找结果的处理与(1)相同,若查找成功,从链首计算时只需计算至Ck-1位置即可与密文C进行比较。
(3)依次类推,直至破解成功。若所有k步操作完成后,仍没有比对成功,则说明破解失败。
1.4 性能分析
相对于散列函数H的计算复杂度,简约函数R的计算通常非常简单,基于链长为k,条数为s的彩虹表,破解一个密码时的性能计算如下:
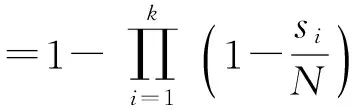
多张彩虹表破解成功率=1-(1-T)t,其中T为使用单张彩虹表的破解成功率,t为彩虹表的张数。
随着t的增大,1-(1-T)t>T,由此可见,采用多张彩虹表可以提高密码破解的成功率,当然,这需要花费更多的时间和存储空间构造彩虹表。
2 分布式计算
为了获得更高的破解成功率和更快的破解速度,需要较快地构造多张尺寸更大的的彩虹表,以及更快的Hash函数计算速度和二分查找速度。这对计算机的处理能力要求非常高,仅依赖于单台计算机(处理器可能是多核)计算速度的提高,远远达不到办案实战的要求。因此需要寻求一种利用现有的资源高效完成复杂任务的方法。一种有效的办法是通过高速网络,将多台计算机连接起来协同工作,并行地构造多张彩虹表,并分布式存储于每台计算机中,在破解阶段,多台计算机并行工作,就可高效快速地完成密码破解任务。
2.1 为什么选择MPI
MPI(Message Passing Interface)是一种并行程序编程模型,可基于消息传递机制开发并行程序。MPI提供一系列消息传递的函数库,这些函数库与具体的语言无关,编程者在使用时可与具体的编程语言绑定,例如C语言、C++语言和FORTRAN语言。也就是说,只要编程者熟悉这些语言中的任一种,就可以很快掌握MPI编程,而且对于原来用这些语言编写的程序,只要稍加修改,调用个别用于并行控制的函数,就能轻松实现原有程序的并行化。
除过MPI之外,Hadoop Map/Reduce也是一种非常流行的并行编程模型。Map/Reduce使用简单,以一种可靠、高容错的方式并行处理上T级别的数据集,但只适合特定任务的并行处理,而且使用不灵活。而彩虹表的构造以及根据彩虹表破解密码,需要大量的计算,不仅要解决数据并行的问题,更要实现并行计算,使用Map/Reduce编程模型,效率和速度无法满足要求。
而MPI并行编程模型以消息传递为基础,相对于Map/Reduce而言,虽然编程难度较大,但并行控制方式更灵活,适合那些用数据并行方法很难实现或者实现代价很高的并行算法。MPI使用的消息传递方式既适用于共享存储多处理机,也可适用于分布式存储多处理机。将多台具有多核处理器的计算机高速连接起来的集群,既有分布式内存,又有共享式内存。这种架构的集群,采用MPI编程模型对处理彩虹表密码破解这类数据量和计算量都非常大的情况非常有效。
2.2 并行程序框架设计
在MPI并行程序设计中, 计算任务需要提前分割成若干个子任务, 然后将它们分配到各个节点的计算机上去执行。执行过程中,各个子任务之间为了协调工作需要进行通信。子任务的划分要根据具体情况调整,以便保持负载平衡, 减少通信开销以提高执行效率。MPI支持主从模式和对等模式,这两种模式分别适用于不同类型的并行计算任务。
主从模式中, 需要设计一个主进程负责任务的划分、分派及计算结果的收集和归并,并负责所有从进程间的网络调度和协调。而从进程则负责接收子任务、完成计算和结果的发送。无论是彩虹表的构造,还是基于彩虹表进行密码破解,在每台计算机上执行的程序都是相同的,各进程之间不需要传输大量的数据,只需要交换消息即可。显然,彩虹表的构造不适合这种主从模式。
对等模式又称为SPMD(Single Program,Multiple Data)模式。在这种模式下,所有进程不分主从,地位相等,均执行同一个程序,但处理不同的数据。这非常适合分布式彩虹表构造和基于彩虹表进行密码破解,每个计算节点上执行相同的程序,但是产生不同的彩虹表,其数据分布式存储在各自的节点上。在破解阶段,每个节点查找各自的彩虹表数据。这样节点之间不需要大量彩虹表数据的传输,只需要传递少量的消息,通信开销小。基于对等模式的彩虹表构造程序基本框架如图1所示,密码破解程序的基本框架如图2所示。
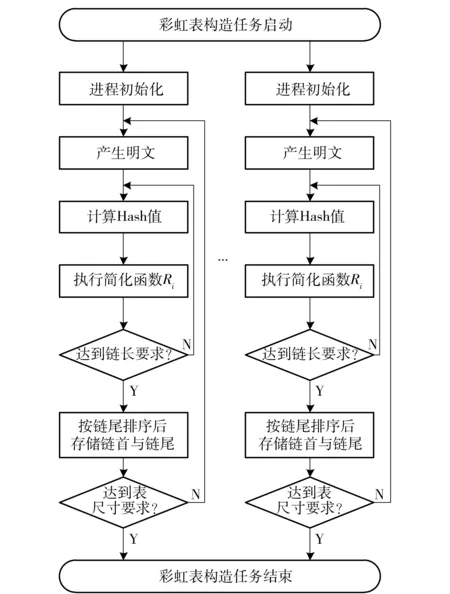
图1 彩虹表构造框图

图2 密码破解框图
在密码破解过程中,只要任意进程破解成功,则表示破解任务完成,这时该进程给其他各进程发送消息,其他各进程收到消息后立即停止各自的工作,整个任务完成。只有每个进程都破解失败,才表示任务失败。
彩虹表是按进程分布存放在每台计算机上,每台计算机都可能存储多张彩虹表。每个彩虹表构造时使用的简约函数系列均不相同,这是减少彩虹表碰撞而产生误警的关键。密码破解时使用的简约函数系列要与彩虹表构造时使用的简约函数一致,否则会出现错误。
3 密码加密流程分析
在利用彩虹表方法破解密码之前,首先需要对密码的加密方式和流程分析清楚才能正确地构造彩虹表,并基于构造的彩虹表完成破解密码工作。下面以Windows操作系统和Linux操作系统为例,说明常用操作系统密码加密以及存储方式。
3.1 Windows密码加密分析
在Windows操作系统中,用户设定或修改密码时,系统先计算密码的哈希值,然后将该哈希值存储在安全账号管理器SAM(Security Account Manager)中。系统采用的哈希算法是LM(Lan Manager)和NTLM(NT Lan Manager)。LM算法的流程如图3所示,NTLM算法的计算流程如图4所示。

图3 LM算法流程
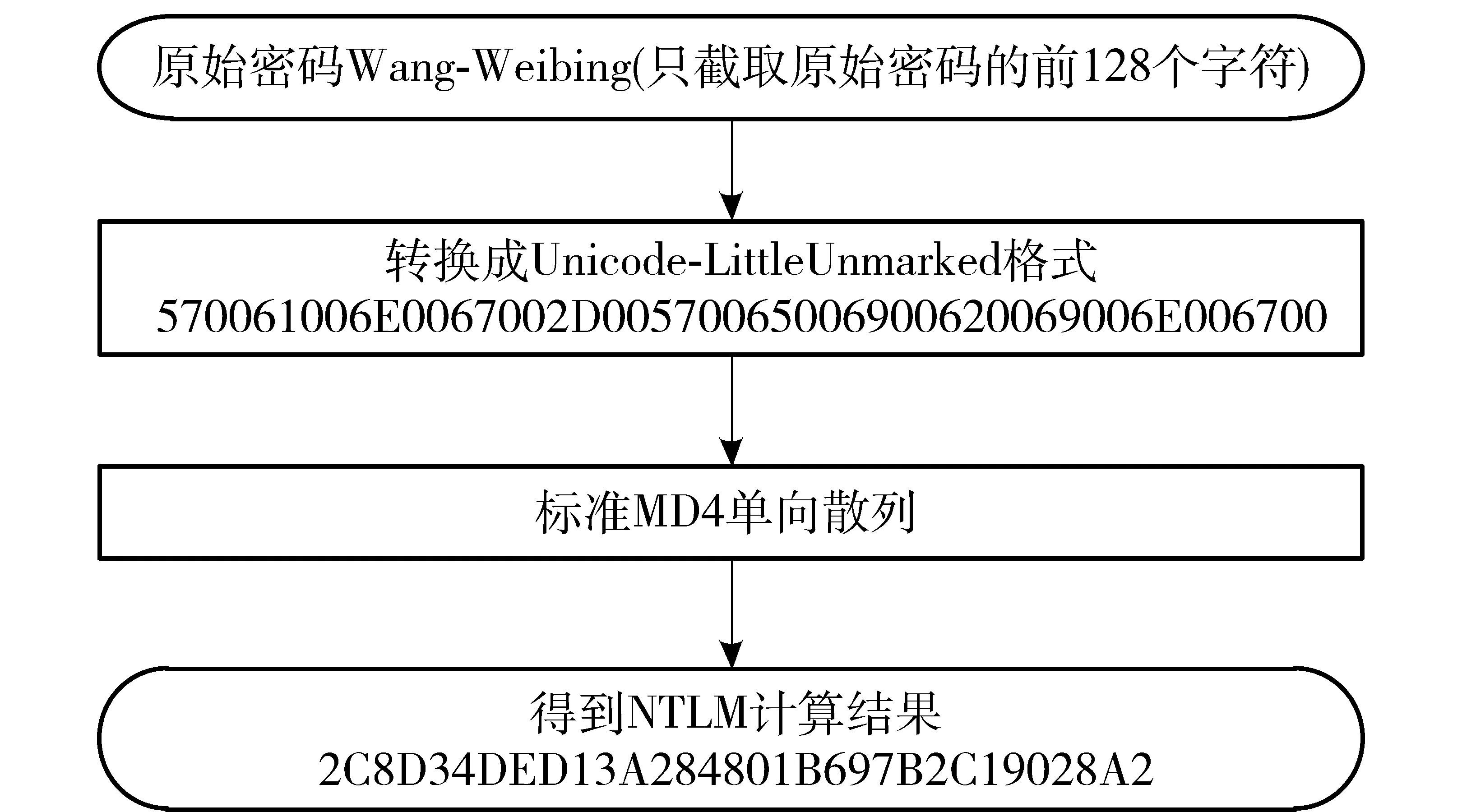
图4 NTLM算法流程
在Windows XP中,通过工具QuarksPwDump得到SAM中的密码哈希值为Administrator:500:25095F8EBC4E5DA67B5219BCA4D8709F:2C8D34DED13A284801B697B2C19028A2:::。其中“Administrator”是用户名,“500”是用户ID,“25095F8EBC4E5DA67B5219BCA4D8709F”是该用户的密码通过LM哈希计算后的值,“2C8D34DED13 A284801B697B2C19028A2” 是该用户的密码通过NTLM哈希计算后的值,两个哈希值均以十六进制字符串表示。
但是在Windows7操作系统中,通过工具QuarksPwDump提取到的超级管理员用户的密码哈希值为Administrator:500:AAD3B435B51404EEAAD3B4 35B51404EE:2C8D34DED13A284801B697B2C190 28A2:::。其中“AAD3B435B51404EEAAD3B435B5 1404EE”是用“0000000000000000”作为密钥对魔幻字符串“KGS!@#$%KGS!@#$%”进行DES加密的结果,“2C8D34DED13A284801B697B2C190 28A2” 则是该用户的密码通过NTLM哈希计算后的值。
3.2 Linux密码加密分析
在Linux操作系统中,每个用户登录密码的哈希值记录在文件/etc/shadow中,该文件的每一行对应一个用户,每行内容分为若干个字段,内容与含义为:
用户名:登录密码的哈希值:最后一次修改时间:最小时间间隔:最大时间间隔:警告时间:不活动时间:失效时间:标志。一个具体的例子如下所示:
root:$6$9lovYHZM$fDVrlQ.etYY/xrF3Hc-AShGVfRKwshcfbZXp3yv3ueHoAFHtfS3nNNuUCxgLz-errzbG9rJtci8vzz8I5h7D.5U1:17193:0:99999:7:::
其中第二个字段“$6$9lovYHZM$fDVrlQ.etYY/xrF3HcAShGVfRKwshcfbZXp3yv3ueHoAFHtfS-3nNNuUCxgLzerrzbG9rJtci8vzz8I5h7D.5U1”就是root用户登录密码的哈希值。分析该哈希值的产生过程,对密码破解非常重要。该字段格式为$id$salt$encrypted,每个部分的含义如下:
id表示使用的哈希算法,可能的取值如表1所示。

表1 Linux登录密码的各种哈希算法
salt是使用各种哈希算法进行计算时的一个干扰字符串,在生成或修改登录密码时由系统随机产生。
encrypted即是对密码进行哈希计算的结果,但不是直接对登录密码进行哈希计算,而是对登录密码和salt进行混合,再进行多次哈希函数计算,然后再经过base64编码的结果。
分析Linux源码可知,具体的哈希计算由函数char *crypt(const char *key, const char *salt)完成,该函数的第一个参数就是用户设定的密码,第二个参数salt是由另一个函数char *crypt_make_salt (const char *meth, void *arg) 生成,参数meth就是哈希算法名称,使用不同的哈希算法作为参数,该函数生成不同长度的随机串。
针对Linux这种带salt的的密码破解问题,构造彩虹链的构造流程要调整,过程如下所示:
其中P0为随机产生的明文空间中的某个密码,S0可使用Linux源代码中函数crypt_make_salt生成,H可以直接使用Linux源代码中的函数crypt。R函数则负责负责从crypt函数的输出中分离出新的明文密码和salt串。利用彩虹表破解密码时,函数形式相应调整即可。
4 实验设计与分析
4.1 可行性测试
实验集群环境由15台Dell服务器搭建,节点机器配置如下: CPU: Xeon E5-2620*2;内存:48 GB;硬盘:500 GB;以太网卡:1 000 Mb/s 全双工;操作系统: CentOS6.8 Linux。
实验是针对目前在侦查实战中最常见的Windows7操作系统的密码破解任务而设计的。Windows7操作系统用户登录密码的加密算法是NTLM,明文由最长128个任意字符组成。考虑到实际案件中的需要,密码空间中的字符串遵循以下规则:
(1) 密码长度不超过8个字符;
(2) 密码字符只包括小写字母、大写字母和阿拉伯数字;
因此,密码空间的大小为:
N=62+622+623+…+628≈2.219×1014
在彩虹表构造阶段,设计每条彩虹链长度为1 000 000,每条彩虹链存储包括链首和链尾不超过30个字节的数据。为了涵盖所有密码空间中的密码,则总的彩虹表大小为:
M=2.219×1014÷1 000 000×30≈6.2G
集群中共有15台机器,每台机器上启动24个进程,共360个进程,每个进程负责产生一个17.6 M的彩虹表,每台机器上的彩虹表尺寸大约423 M。
经过实验测试,按照以上设计,完成彩虹表的构造大约需要45小时。基于这样的彩虹表,给定100个任意密码的NTLM散列值,平均每个密码破解时间<1分钟。
4.2 对比测试
针对现有实验条件,设计不同大小的密码空间进行比对。集群中有15台机器,每台机器上启动24个进程。需要构造的彩虹表总尺寸和预计构造时间如表2所示。
按照以上设计,在集群中启动程序,构造彩虹表以及基于彩虹表破解100个任意密码的平均时间如图5和图6所示。
由实验结果可知,随着密码限长以及构成密码的字符种类增多,密码空间的大小呈指数增长,构造彩虹表的空间成本和时间成本也呈指数增长,这就需要投入更大成本增加更多的计算结点。

表2 不同密码限长所需构造的彩虹表尺寸

图5 不同密码限长时彩虹表构造时间

图6 不同密码限长时平均破解时间
一旦彩虹表构造完成,破解密码所花时间随密码限长的增加而线性增加。分析原因,虽然彩虹表的尺寸随密码限长的增加呈指数增加,但是彩虹链的长度保持不变,破解密码时所需要进行哈希运算的次数不变,只是增加了待查询的彩虹表中所有链尾所构成的线性表长度。但是由于采用的是二分查找,查找所需时间随彩虹表的长度增加而呈对数增加,所以总的破解时间增加的很慢。
5 结束语
本文首先分析了彩虹表的基本原理,包括彩虹表的构造方法和基于彩虹表破解密码的方法,研究了常见操作系统登录密码的加密流程。根据这些研究结果,提出了利用MPI分布式编程模型实现构造彩虹表以及基于此彩虹表破解密码的过程。通过实际编程实验表明,这些方法是有效的,能满足实际工作需要。
下一步将重点研究以下几个问题:彩虹表的存储模式,探讨使用Redis缓存服务器存储彩虹表,在内存中查找彩虹表,进一步加快破解速度;优化简化函数系列的设计,尽量减少误警率;研究彩虹表的大小和彩虹链的长度对破解速度的影响,找出最优或次优参数。
[1] HELLMAN M. A cryptanalytic time-memory trade off[J]. IEEE Transactionson Information Theory, 1980,26(4):401-406.
[2] OECHSLIN P. Making a Faster Cryptanalytic Time-Memory Trade-Off[J]. Lecture Notes in Computer Science, 2003,2729(4): 617-630.
[3] BORST J, PRENEEL B, VANDEWALLE J. On time-memory trade off between exhaustive key search and table precomputation[C]. Symposium on Information Theory in the Benelux,1998:111-118.
[4] 李昕,曹天杰,米国粹,等. 基于分布式环境下的彩虹表密码攻击[J]. 计算机应用与软件,2011(2):290-293.
[5] 李永达,王党辉,黄小平. 采用GPU的ZIP密码恢复算法[J]. 计算机工程与应用,2015,51(2):190-193.
[6] 仇李寅. 基于的扩展彩虹表生成研究[D]. 上海:上海交通大学,2011.
[7] 陈国良,安虹,陈嶙,等. 并行算法实践[M]. 北京:高等教育出版社,2004.
[8] Windows LM/NTLM HASH加密及获取工具. http:∥blog.csdn.net/gscaiyucheng/article/details/9151257.
(责任编辑 于瑞华)
王伟兵(1977—),男,陕西歧山人,硕士,讲师。研究领域为网络攻防与电子取证。
TP309.7
