振荡浮子阵列间距的数值模拟❋

史宏达, 王 东， 杨智鸿

(1.中国海洋大学工程学院，山东 青岛 266100；2.中国海洋大学海洋工程山东省重点实验室，山东 青岛 266100； 3.中交水运规划设计院深圳公司，深圳 518067)

振荡浮子阵列间距的数值模拟❋

史宏达1,2, 王 东1， 杨智鸿3

(1.中国海洋大学工程学院，山东 青岛 266100；2.中国海洋大学海洋工程山东省重点实验室，山东 青岛 266100； 3.中交水运规划设计院深圳公司，深圳 518067)

振荡浮子式波浪能发电装置是一类重要波浪能利用设备。但是这类设备的单体功率较低，为提高总输出功率，阵列式开始出现并成为研究热点。阵列式是指将若干浮子按照一定规则排列在海域中，通过整流设备将所获取的能量进行整合，统一发电并利用。文中介绍的研究其目的就在于研究浮子阵列的布置方式。在研究过程中利用CFD软件FLOW3D进行三维数值模拟，获得了浮子在实际波况条件下的波浪场分布情况。通过多属性决策方法确定优选排列型式，计算空间尺度，并进行验证。实验结果表明：在实验条件下后方浮子应排列在前方浮子正后方(行列应垂直布置)，同排和同列相邻浮子优选间距为6.9 m。

振荡浮子；波浪能；布置；间距；数值模拟

波浪能的开发与利用已经历了百余年时间[1]。在众多的波浪能发电装置中，振荡浮子式直接与波浪接触、结构简单、转化效率高而得到了国内外专家的关注,其研究工作目前仍是热点[2-4]。

虽然振荡浮子的转化效率高，但是单个浮子的功率仍不满足大规模开发利用的要求。概括来说，有三种方法被用于克服这个困难，这三种方法可表述为改进结构、实时控制和阵列布置。改进结构是比较传统的方法，它既包括改变浮子形状、尺度、重量等[5]；也包括改变装置原理，除利用浮子垂荡运动外，还利用横荡、纵荡或其它三个方向摇动的能量[6]。实时控制是最新提出的概念，在实时控制中浮子的质量和电机阻尼系数不再是一个常数，而是利用探测系统反馈的前方波浪信息，对浮子的质量或电机阻尼进行实时调节，使浮子任意时刻都处于共振或近似共振状态，从而提高浮子的输出功率。阵列布置则是指将若干浮子排布在海域中，通过整流设备将所获取的能量进行整合，统一发电并利用。

上述三种方法中，改进结构和实时控制只能有限的提高浮子的输出功率，且会使结构更加复杂。而阵列布置则可以使简单的升沉式浮子大幅提高输出功率，并且在理论上输出功率无上限。国内外均对这种型式进行了研究[7-8]。

浮子单体的形状、尺度、重量，传动系统，浮子阵列的整流系统，锚固系统均有专门的研究。浮子布置与间距，则没有专门的研究。浮子的布置与间距直接影响浮子的透射波、绕射波和辐射波以及相互之间的叠加情况。因此，文中研究的目的即浮子的布置形式和间距。依据工程项目实际海域情况给出工况。进行单个浮子数值模拟给出浮子电机阻尼施加形式。进行浮子阵列单元数值模拟，给出浮子单元所在海域的波浪能分布情况，通过多属性决策方法给出优选形式，最后计算出相关参数。

1 模型确立

1.1 模型选择

浮子的阵列布置有两种方法，列式布置和行列布置。列式布置将浮子布置成单列或两列。最具代表性的是丹麦的WaveStar。装置中浮子顺浪排列，对原波浪场影响较小，相邻浮子之间影响也较小；但长度方向跨度比较大，占用海域面积较多。行列布置将浮子布置成多行多列。最具代表性的为挪威的FO3。该装置占用海域面积小，利于拓展；但浮子之间的影响较为明显。

文中采用行列布置。该模型是四浮子组合型基础上的扩展，也是FO3的改进。它取消了4个立柱，增加了一个平台，减小了结构对浮子的影响。同时方便靠船(见图1)。

图1 浮子阵列示意图

1.2 模型参数

模型参数含环境参数、浮子参数、布置参数。环境参数包括波参数与水深；浮子参数包括浮子尺度、密度和电机阻尼；布置参数包括布置角度与间距。其中电机阻尼和布置参数是待定参数，其它参数见表1。

表1 条件参数表

2 电机阻尼力的推算

2.1 阻尼形式

前人基于线性理论推算出，电机施加在浮子上的阻尼力符合式(1)[9]。加入液压系统后，阻尼力中非线性部分不再可以忽略。以水轮机相似定律为出发点，结合伯努利方程推算出的阻尼力形式如式(2)[10]。

FPTO=Cv+K，

(1)

FPTO=kv2。

(2)

2.2 最优阻尼系数的推算

最优阻尼系数的推算分为两部分。一为半理论方法。既先用无负载的数模取得浮子空载速度，然后计算加入负载后的阻尼力，净重力和波浪力的变化量，按式(3)用离散化求解浮子时程速度，进一步求解平均功率。净重力变化量ΔG、阻尼力FPTO分别按式(4)、式(5)计算。波浪力变化量ΔFbo经分析小于3%，已忽略。一为数值方法。取若干k值，计算电机阻尼力导入Flow3d模型进行数值模拟后,计算平均功率。再给出最优阻尼系数。

本章数学模采用长200 m，宽3.2 m，深4 m的水槽(其中水深2 m)，浮子参数见表1。浮子设为耦合运动形式，即浮子和水质点的运动通过连续性方程、运动学方程结合外力计算得来。

(3)

(4)

(5)

计算结果见图2。实线为半理论方法的结果，点状为数学模型实测资料。计算结果与实验结果表现出同样的规律。随着k值的增大，输出功率先增大后减小，并在k=20 000 kg/m附近取得功率峰值。由于在半理论方法中忽略了动水压力的变化，因此所求得的k值小于实验方法。数学模型实验显示，在k=25 000 kg/m时取得峰值，峰值功率为1.84 kW。

因此在下章绕射分析中采用k=25 000 kg/m。

图2 F=kv2时k-P图

3 实验与分析方法

实验目的是用数模研究绕过浮子后波浪场分布情况，并据此给出浮子的阵列布置方案及相关参数。

3.1 实验方法

假设单排浮子数量较多，则除两侧浮子外，其它浮子运动有重复性。 可取出仅含少数浮子的阵列单元作为分析对象。用重复性推算其它浮子的运动特性。图3为两排浮子时的阵列单元。为提高精度和效率，数模水槽分成四段。网格区域划分如表2所示，水槽高度-2～2 m，静水面为0,宽度方向为2d+2g,d为浮子直径，g为间隙尺度。第一排浮子中心x坐标为零，其它浮子参数见表1。运动形式仍设为耦合运动。

图3 多浮子实验水槽示意图

表2 水槽功能区表

实验共分为三部分：

(1)布置一排浮子，取不同的浮子间距，研究浮子后方波浪场分布规律，并确定布置方案。

(2)布置两排浮子，验证最优位置是否输出最大功率。即确定波能集中处即浮子输出功率最大处。

(3)布置三排浮子，验证波浪场是否具有重复性。

3.2 分析指标

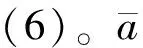
(6)

为表征浮子接受能量与平均波高的关系，定义了等效波高。等效波高指待安装浮子即将占用区域内的波高以微元面积为权的平均波高。定义如式(7)。

(7)

4 实验结果与分析

4.1 单排浮子实验

实验中仅放置单排浮子，目标在于分析波浪绕过单排浮子之后的能量分布情况。本组实验按本文的方法施加电机阻尼力，需对两侧的半浮子模型阻力减半。本组实验共设计10种工况，分别对应1.6～6.4 m10种不同的浮子横向间隙。

实验结果表明，浮子后方透射波、绕射波与辐射波相互叠加，形成了有规律的能量分布。文中仅给出有代表性的4张平均波高等高线图，以方便读者定性观察分布情况(见图4)。

图4波浪场随间隙而变化。间隙1.6 m时后方波浪场较平衡(见图4左上)。2.4 m后出现明显的波能集中，集中区域分布于浮子与浮子间隙的正后方，3.2 m时第一个波浪能集中区域完全形成(见图4右上)。其后第一波能集中区明显被拉长，其它集中区域位置变化不大，且均于浮子后方33 m附近处形成稳定波浪场。

图4 有效波高等高线图

为定量研究单排浮子后方的波浪能集中情况，确定浮子布置方式，用等效波高(请参考3.2节)的概念对后方波浪场的极值进行分析(见表3～4)。极值指同一波向线上等效波高斜率为零时的极大值。

表3 浮子后方有效波高极值表

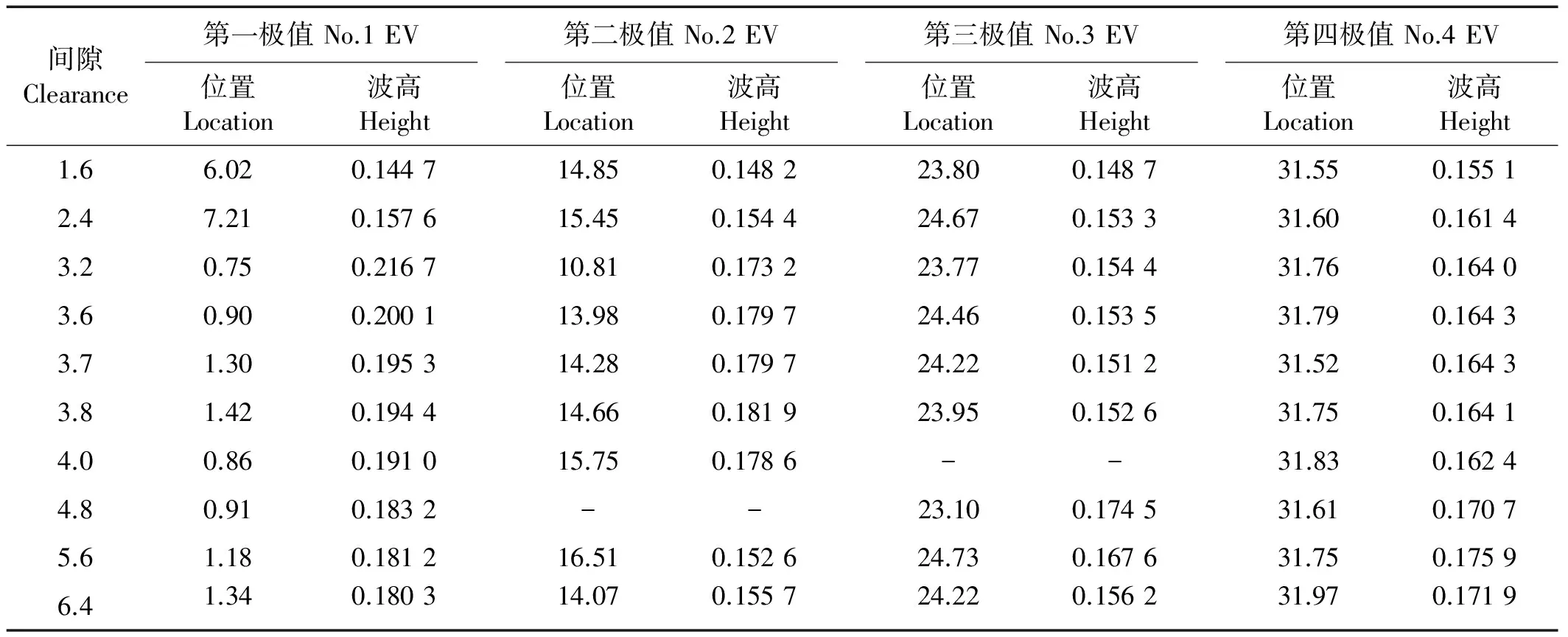
表4 间隙后方有效波高极值表

从表3～4可得到波能极值分布的几个基本规律:

(1)随着位置的后移，极值逐渐变小，因而利用前面的能量集中区比后面的要更加有效；

(2)第一极值规律非常明显：随间隙的加大，极值点向后移动，同时等效波高也明显变小。

(3)第二、第三极值由于辐射波与绕射波能量相当，在这一区域内极值极不稳定,不建议利用。会发生相互覆盖。但这两个极值位置较为固定。

(4)第四极值位置非常稳定，界于31.52～31.97 m之间。可以视为稳定波浪场的起始位置。

由此，可以提出4种布置方案，表述如下：

(1)横向间距较小，后方波浪场不表现集中现象、纵向间距也可以密集布置；(2)横向布置适度，并将后方浮子放在33 m后的稳定波浪场中；(3)横向布置适度，后方浮子置于前方浮子后方的波浪能集中位置；(4)横向布置适度，后方浮子置于前方浮子间距后方的波浪能集中位置。

4种方案的优缺点总结表5。

表5 各方案优缺点

本文利用多属性决策方法对这4种方案进行比选。首先确定了7项重要指标，并根据重要性确定权重。再对各方案的属性赋值(见表6)。由于所赋属性值均为定性指标，为了便于分析，采用Bipolar法将指标定量化。得到判断矩阵后，求解判断指标见表7。

表6 属性值表

表7 判断指标表

方案III为优选方案，方案I次之，方案II和方案IV不推荐。经计算，当横向间距6.9 m时(对应横向间隙3.7 m)，优选纵向间距也为6.9 m。经验算该间距对正向入射波、横向入射波以及斜向45°入射波都有良好的适应性。

与动力特性物模实验、液压系统物模实验结果对比显示：单排浮子后方波浪场存在波浪能集中现象，且在可观察点位上比波高相同(比波高定义为某点波高与入射波高的比值)。数值模拟结果是正确的。

液压系统物模实验参数与数模参数对比见表7。除水深与入射波波高略有差别外,其它条件均类似。

表8给出的是物模结果对数模结果的验证。在同一位置处，物模与数模的比波高在误差允许的范围内相同且规律相同。24 m附近为第三极值，比波高分别为0.85 m与0.86 m，28 m处已进入第四极值上升处，但比波高仍小于24 m处，分别为0.81和0.83 m。体现出相同规律。

表8 模型参数对比

表9 模型参数对比Table 9 Comparison of model parameters

4.2 双排浮子实验

双排浮子实验目的是验证单排浮子实验的布置方案的正确性，模型、浮子与阻尼力施加方法均不变。

本组实验共分3大组，6种工况(见表10)。列间距不变，改变行间距。根据测得的第二排浮子的功率，判断浮子布置于波能集中区能否输出最大功率。3个位置计算所得的结果见表11。最优位置6.9 m处功率最高，因此单排浮子结果是可信的。

表10 工况表Table 10 Experiment condition

表11 第二排浮子功率Table 11 Power from the buoys in row 2

图5是浮子行间距为6.9 m时后排浮子空载(上)和加载(下)情况下的平均波高等高线图(50条等高线)。

图5 双排浮子时有效波高等高线图Fig.5 SWH Contour when two row of buoys were set

图5表明：(1)由于第二排浮子的存在，两排浮子中间的波能集中处能量变大且位置后移；但后绪实验表明，此处安置浮子会影响后方波浪能集中区的分布，并且考虑到阵列重复性与浪向适应性，此处不再安置浮子。(2)后方波浪场的能量减小，并出现了与第一排类似的集中现象。第二个现象表明波浪能集中现象是在空间上是重复性的。

4.3 三排浮子实验

三排浮子实验是为验证重复布置的可行性。即N排浮子后波浪场会否重复类似的能量集中现象与分布特征，从而重复前面的布置，直至波能不足。

图6 三排浮子有效波高等高线图

实验结果如图6所示(75条等高线)。加载后第三排浮子后方的波浪场在相同位置出现了波浪能集中现象，波浪场在空间具备重复性。同时需要注意到，此时波能已经较小，阵列布置可重复布置的行数是有限的。在本研究中，所取波高样本有限，不能通过此方法确定浮子可重复排列的行数。

5 结论

经过四组三维数学模型实验结果的分析，可以得出以下3个结论：

(1)加入液压系统的阻尼力形式呈现明显的非线性，它与浮子速度的平方呈正比。文中提出了解算电机阻尼系数的方法，并计算特定波况条件下的优选电机阻尼系数。

(2)单排浮子后方波浪场会形成波能集中区域，实验证明利用这些区域比其它位置更有利于波能的提取。且波浪能集中现象在空间上具有重复性，前三排浮子与后方波浪能第一极值间距见表12。在波浪能充足的情况，浮子排可重复布置。在实验条件下，浮子应正向布置，浮子的横向、纵向间距均取6.9m。其它工况需按文中方法补充实验，以确定间距。

表12 极值位置

(3)若浮子每行布置单体过多，则后方浮子接受的波浪能会减小，可布置的排数有限。但本实验不能确定可布置的排数。如浮子横向布置有限，则浮子可布置的排数可有效加长。因此在不确定浪向的情况下，行列布置较行式布置更有优势。

[1] Antonio F，Falcao O. Wave energy utilization: A review of the technologies[J]. Renewable and Sustainable Energy Reviews, 2010(14):899-918.

[2] Jamie Goggins, William Finnegan. Shape optimization of floating wave energy converters for a specified wave energy spectrum[J]. Renewable Energy， 2014,71(11):208-220.

[3] Harne R L， Schoemaker M E, dussault B E, et al. Wave heave energy conversion using modular multistability[J]. Applied Energy, 2014,130(10):148-156.

[4] Yu Yi-Hsiang, Li Ye. Peynolds-Averaged Navier-Stokes simulation of the heave performance of a two-body floating-point absorber wave energy system[J]. Computers & Fluids, 2013, 73(15):104-114.

[5] 高人杰.组合型振荡浮子波能发电装置研究[D]. 青岛：中国海洋大学, 2012. Gao Renjie. Study on Combined Oscillating Buoy ware Energy Converter [D]. Qindao: Ocean University of China, 2012.

[6] 史瑞静，樊小朝，李凤婷. 波浪能发电点头鸭式稳态绕流数值模拟研究[J].山东电力高等专科学校学报, 2013(2):6-9. Shi Rui-Jing,Fan xiao-Zhao. Li feng-Ting. Numerical Simulation Research of wave Power aeneration "Nodding Duck" Stedy flow [J]. Jouraol of Shandouy Electric Porer College 2013(2): 6-9.

[7] Lendenmann H, Stromsem K, Dai P M, et al. Direct generation wave energy converters for optimized electrical power production[C]: Proceedings of 7th European Wave Tidal Energy Conference.Porto:Portugal, 2007.

[8] 黄燕,马哲,史宏达,等. 一种新型振荡浮子式波浪能发电装置的研究构想[J]. 中国水运, 2012,12(1):114-116. Huang Yan, Ma Zhe, Shi Hong-Da, et al. Study and conceive of a new type hearing buoys ware energy generator [J]. China water Transport, 2012,12(1):114-116.

[9] Budal K, Falnes J. Power generation from ocean waves using a resonant oscillating system[J]. Maring Science Communication, 1975,77(1):1-25.

[10] 刘大凯. 水轮机[M]. 第3版. 北京：中国水利水电出版社. 1997. Liu Da-kai. Hydroturbine [M]. Ver 3. Beijing: China Woder Porer Press, 1997.

[11] 邹志利. 海岸动力学[M]. 第4版. 北京：人民交通出版社. 2009：39-41. Zhou Zhi-Li. Coactal Hydrodyramics [M]. Ver. 4. Beijing: China Communicaions Press, 2009:39-41.

[12] 邱大洪. 工程水文学[M]. 第3版. 北京：人民交通出版社. 1999：116-118. Qiu Da-Hong. Engineering Hydrology [M].Ver 3. Beijing: China Commurications Press, 1999: 116-118.

责任编辑 陈呈超

Numerical Simulation on the Interval Between Heaving Buoys

SHI Hong-Da1,2,WANG Dong1,YANG Zhi-Hong3

(1.College of Engineering, Ocean University of China, Qingdao 266100,China; 2.Shandong Key Laboratory of Ocean Engineering, Ocean University of China, Qingdao 266100,China; 3.CCCC Water Transportation Planning and Design Institute, Shenzhen Company, Shenzhen 518067,China)

Heaving buoys device is a very important form of wave energy utilization. However the power by single buoy is very small. To improve the total power output, array layout appeared and became the hot point of research. It means to place the buoys in the ocean in rows and columns, using rectifying device to integrate the power by different buoys and make use of it. The aim of research introduced by this article is to study the layout method of the buoys. In this research the CFD softwave named FLOW3D is used to carried out a series of 3 dimention numerical simulation. Data from these numerical simulation describes the wave energy distribution. With this data, we worked out the best plan by method of multiple attribute decision making, the best distance between buoys, and test the correctness of it. The result suggest buoys should be placed just at the back of the former buoys(which means the rows and the columns should be perpendicular), and the distance of the buoys in same row or column should be 6.9m in the setted condition.

heaving buoys;wave energy;layout;distance;numerical simulation

国家高技术研究发展计划项目(2012AA052601);国家自然科学基金项目(41376100)资助. Supported by the National High Technology Research and Developmeut Program of China(2012AA052601);National Natural Science Foundation of China(41376100)

2015-01-19;

2016-05-10

史宏达(1967-)，男，教授，博导。E-mail:hd_shi@ouc.edu.cn

TK79

A

1672-5174(2017)05-106-07

10.16441/j.cnki.hdxb.20150012

史宏达,王东，杨智鸿.振荡浮子阵列间距的数值模拟研究[J].中国海洋大学学报(自然科学版),2017, 47(5): 106-112.

SHI Hong-Da,WANG Dong,YANG Zhi-Hong.Numerical simulation on the interval between heaving buoys[J].Periodical of Ocean University of China, 2017, 47(5): 106-112.