内衬混凝土对波形钢腹板刚构桥扭转和畸变性能的影响
2017-04-09刘保东李祖硕陈海波
刘保东,胥 睿,李祖硕,陈海波
(1.北京交通大学 土木建筑工程学院,北京 100044;2.交通运输部公路科学研究院,北京 100088)
波形钢腹板连续刚构桥作为一种钢混组合结构以波纹型钢腹板代替了传统混凝土腹板和平钢腹板,充分利用了钢材的抗剪能力和混凝土抗压能力,提高了材料的使用效率,具有自重轻、跨越能力大、受力明确、避免腹板开裂等突出优点[1]。由于以上诸多优点,该桥型在国外铁路桥梁中已经得到实际工程运用[2],国内也展开了相关研究[3]。由于列车对梁体多为偏心加载,对梁体整体刚度要求较高[4],因此有必要对该类桥型的扭转和畸变性能改善方法进行研究。文献[5]对波形钢腹板简支箱梁进行了抗弯性能的研究,发现在组合结构受力性能中,可以忽略波形钢腹板的抗弯性能。文献[6—7]通过波形钢腹板简支箱梁扭转和畸变性能的试验研究,得出偏心荷载作用下波形钢腹板简支箱梁的扭转和畸变效应明显,在进行设计和计算中应该对其重视;针对波形钢腹板产生较大的翘曲剪应力,设置一定数量的横隔板可以有效抑制箱梁的翘曲效应。文献[8]对波形钢腹板和混凝土腹板连续刚构桥进行了模型对比试验及分析,发现波形钢腹板连续刚构桥较普通混凝土腹板连续刚构桥抵抗扭转与畸变的能力弱。文献[9—11]对波形钢腹板简支箱梁的扭转与畸变效应进行了分析,建立了波形钢腹板箱梁扭转、畸变的基本分析方法,提出减小波形钢腹板箱梁翘曲正应力的工程措施,并对横隔板设置最大间距进行了相关研究。综上研究表明:波形钢腹板的抗弯刚度相对较小且扭转作用显著,需要实施加强措施。除了采取设置横隔板措施外,文献[12]提出在桥墩台顶横隔板外一定范围内的波形钢腹板内侧浇筑混凝土,采用焊钉及与翼缘焊接的钢筋网进行完全连接,形成组合结构改善受力性能,这有利于波形钢腹板箱梁截面剪应力的流畅传递,同时可以增大波形钢腹板的抗屈曲性能,并起到缓和局部应力的作用。文献[13]通过对内衬混凝土钢混组合段3种剪力分配计算方法的对比,研究了内衬混凝土钢混组合段抗剪验算方法的差异。文献[14]通过有限元分析和理论计算,研究内衬混凝土的厚度对波形钢腹板抗剪性能的影响,结果表明,施工中采用内衬混凝土能够有效扩大腹板的抗剪面积,分担腹板承担的剪力。文献[15]结合试验研究,发现内衬混凝土可限制波形钢腹板梁受压翼缘的屈曲,提高组合梁的弯曲强度与延性,并提出了考虑内衬混凝土时桥梁弯曲强度的计算方法。
综上可知,内衬混凝土对改善波形钢腹板组合桥梁力学性能作用明显。因此随着波形钢腹板箱梁在铁路桥梁建设中的逐步推广应用,应对内衬混凝土的设置进行深入研究。目前对内衬混凝土尚未有明确的设计方法和参数标准,且在内衬混凝土对波形钢腹板连续刚构桥扭转和畸变性能影响方面的研究较少。本文先通过模型试验,测试分析内衬混凝土对波形钢腹板连续刚构桥扭转和畸变性能的影响;然后建立有限元模型,通过控制变量法分析内衬混凝土几何尺寸对波形钢腹板刚构桥扭转和畸变性能的影响,为波形钢腹板内衬混凝土的理论研究和实际工程设计提供依据。
1 模型的静载试验
1.1 试验模型
本试验依托2座变截面连续刚构桥试验模型。模型为2.4 m+3.6 m+2.4 m三跨变截面连续刚构桥(单箱单室),箱梁截面高度的变化范围为33~49 cm,在边跨端部和墩顶设置横隔板。1#模型为未设置内衬混凝土的波形钢腹板连续刚构桥,2#模型为设置内衬混凝土的波形钢腹板连续刚构桥,梁体和桥墩之间通过钢构件实现墩梁固结。受力钢筋采用直径为12和10 mm的HRB335钢筋,构造钢筋采用直径为8 mm的R235钢筋。预应力钢筋采用φj15.2 mm钢绞线。采用Q235钢材制作波形钢腹板,采用C40混凝土制作梁体,采用C30混凝土制作桥墩。主梁一般构造如图1所示,无内衬混凝土和有内衬混凝土波形钢腹板箱梁的横截面如图2和图3所示。
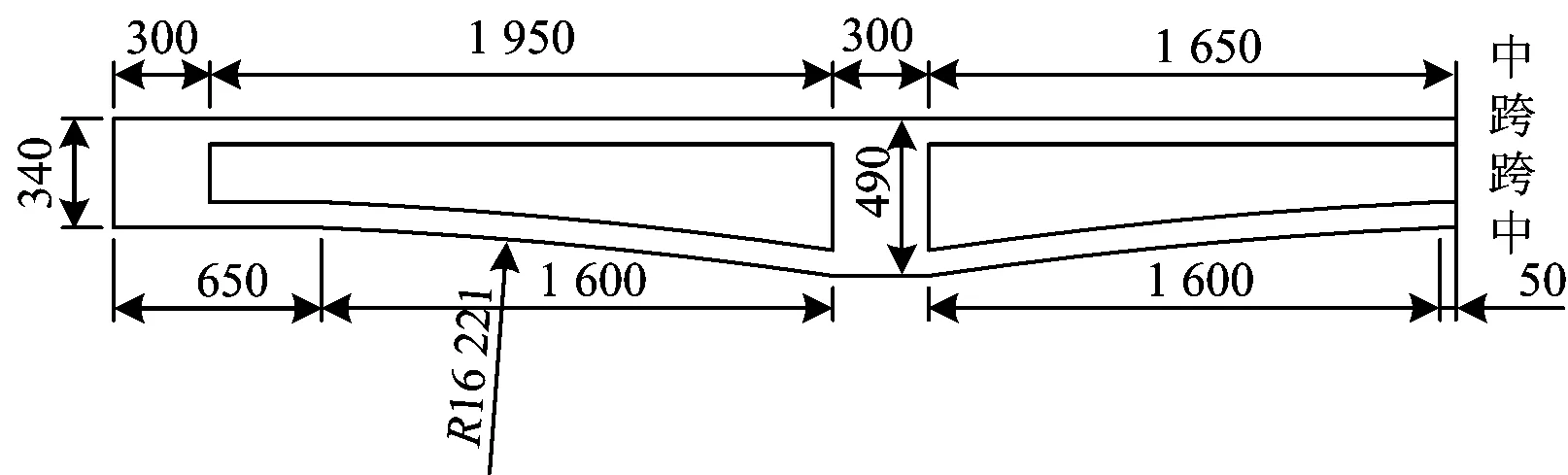
图1 主梁1/2立面图(单位:mm)
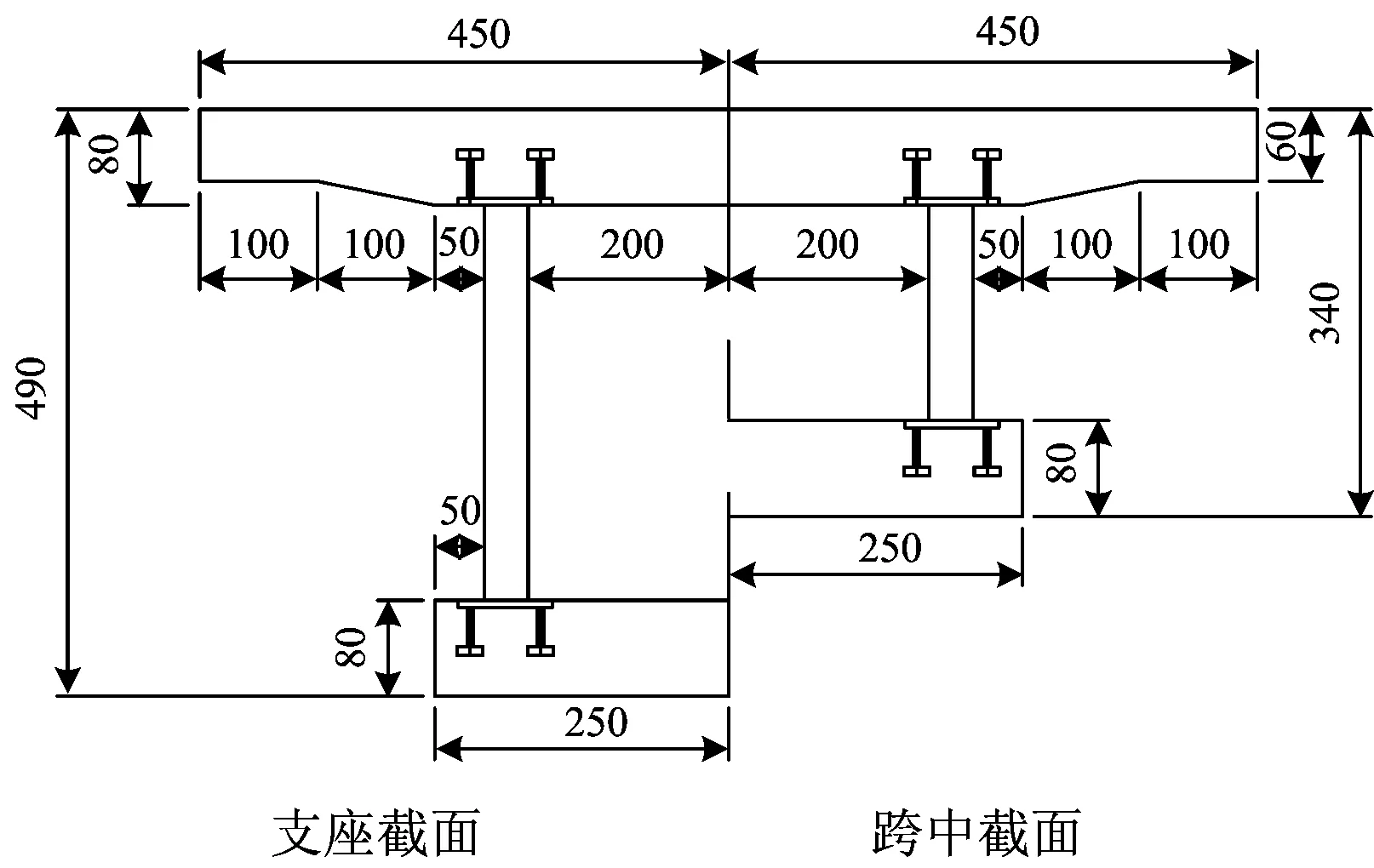
图2 1#模型桥箱梁横截面(单位:mm)
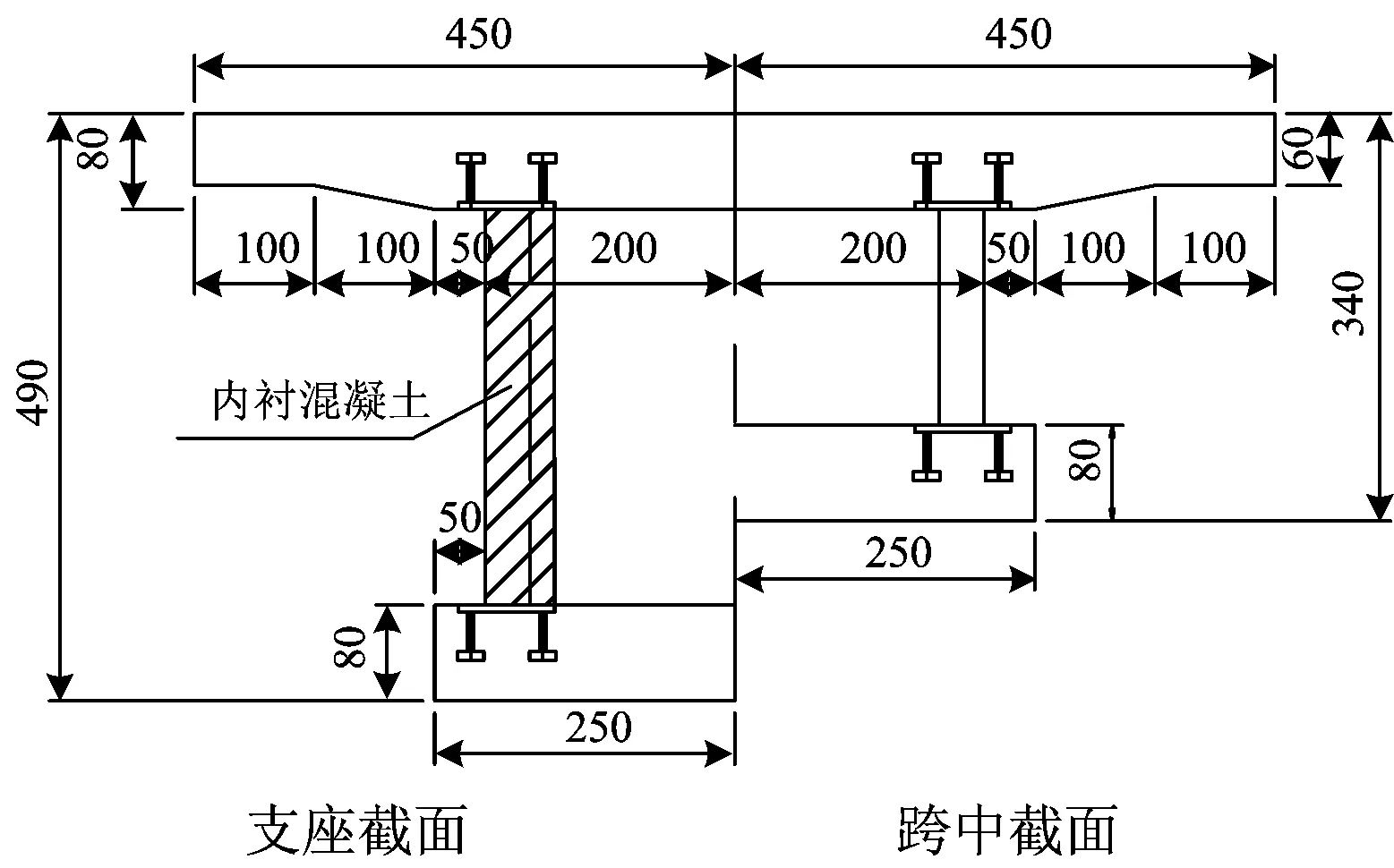
图3 2#模型桥箱梁横截面(单位:mm)
波形钢腹板几何尺寸如图4所示。腹板与混凝土顶底板的连接采用剪力钉,焊钉采用规格GB/T 10433 φ13 mm×40 mm。
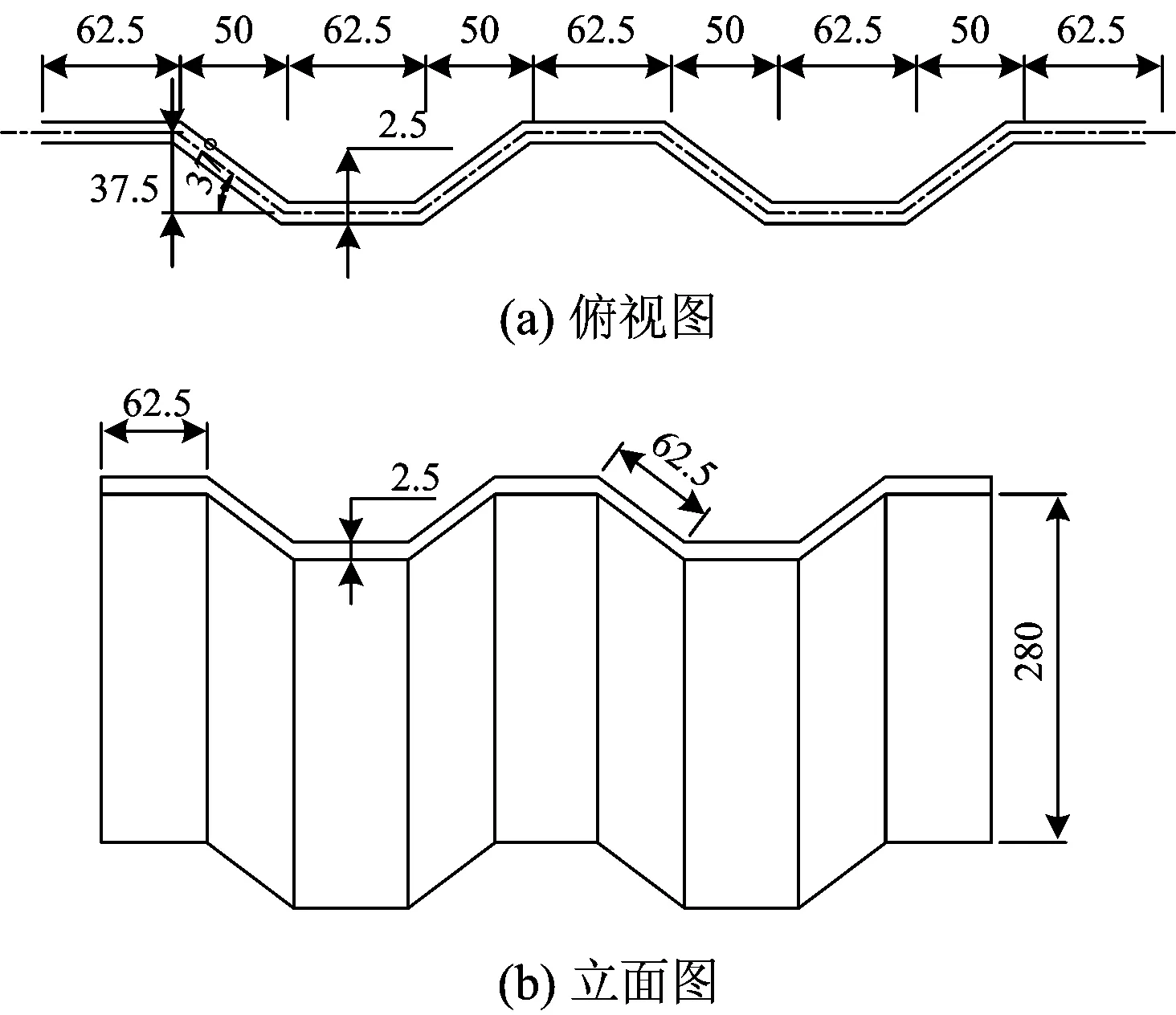
图4 波形钢腹板几何尺寸图(单位:mm)
1.2 测点布置
1.2.1位移测点
竖向位移各测试断面在纵桥方向的位置如图5所示,每个断面在左右腹板位置各布置1个测点,使用千分表测量模型的竖向位移。

图5 位移测点纵桥方向布置图
1.2.2应变测点
在箱梁跨中1/2及1/4截面顶底板粘贴应变片,测量混凝土纵向应变,具体布置情况如图6和图7所示。使用静态数据采集系统测量应变。
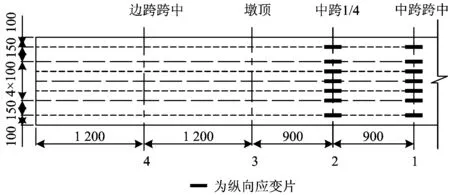
图6 箱梁顶板应变测点布置(单位:mm)
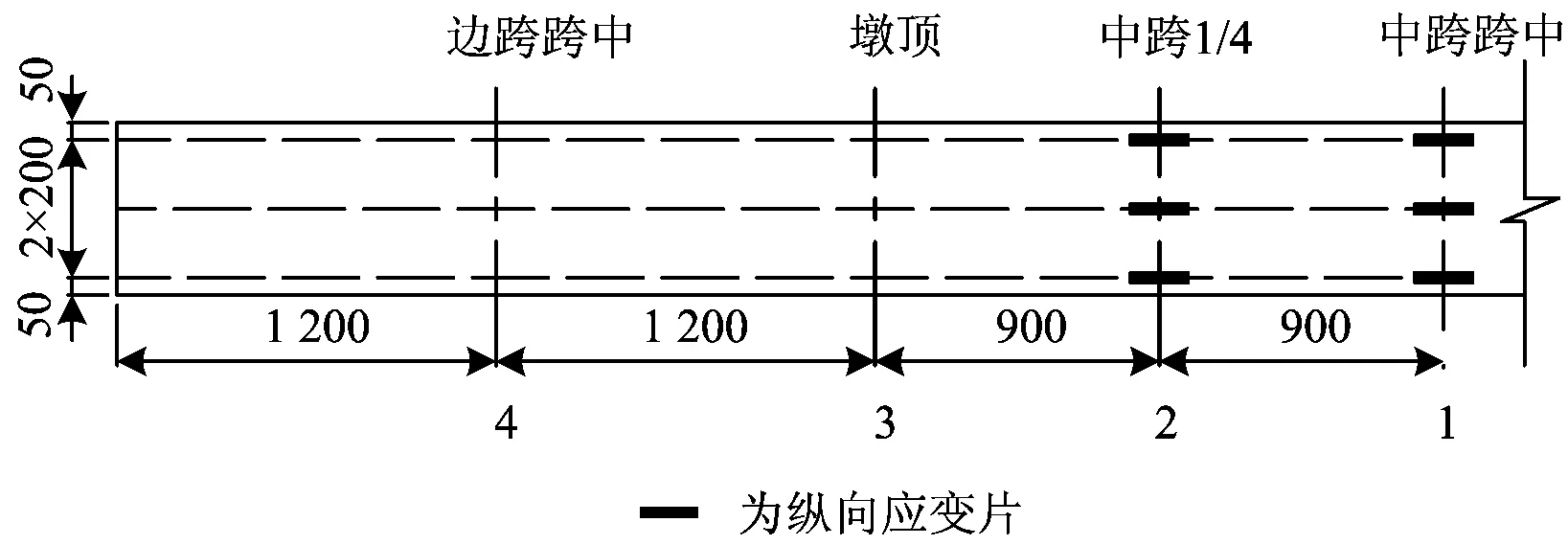
图7 箱梁底板应变测点布置(单位:mm)
1.3 加载方案
试验采用图8所示的4点对称加载和图9所示的2点偏心加载,图中P为荷载。
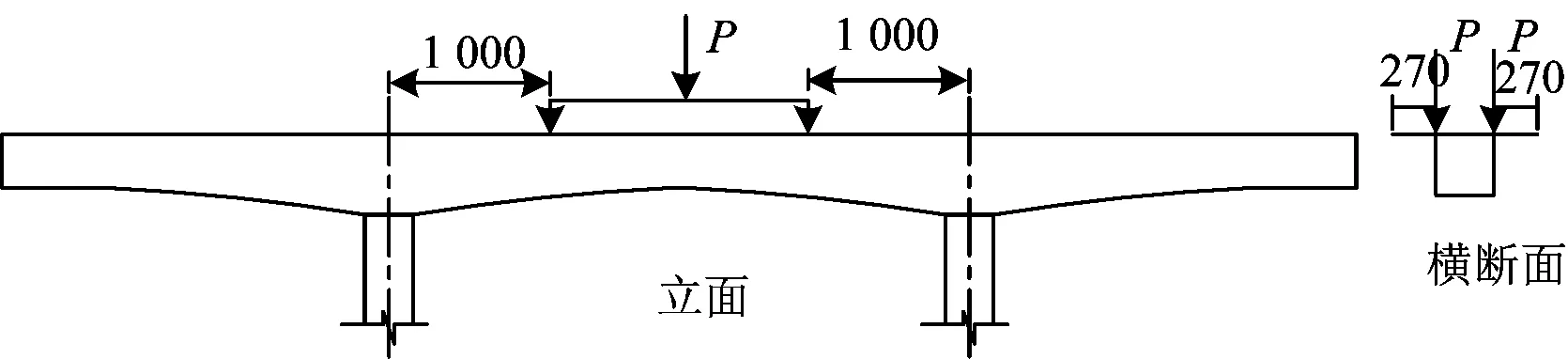
图8 对称加载示意图(单位:mm)
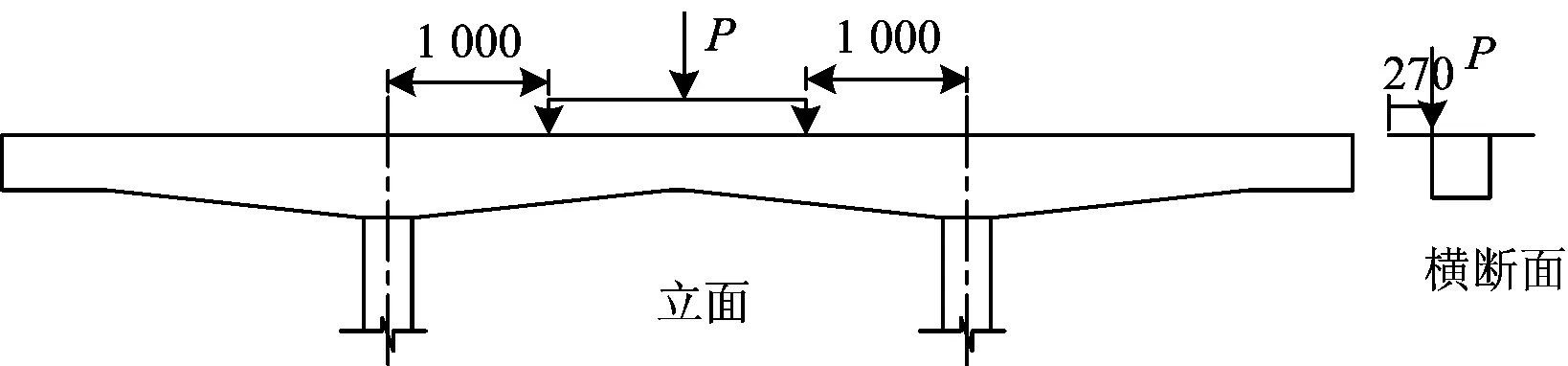
图9 偏心加载示意图(单位:mm)
分8级加载,每级增加10 kN,每增加1级荷载静置5 min后读取相关数据,至80 kN时停止加载。
2 静载试验分析
图10和图11分别列出了1#和2#模型桥在对称荷载、偏载作用下中跨跨中截面挠度,对称荷载时挠度取值为同一截面2个测点的平均值,偏载作用时取偏载一侧挠度。
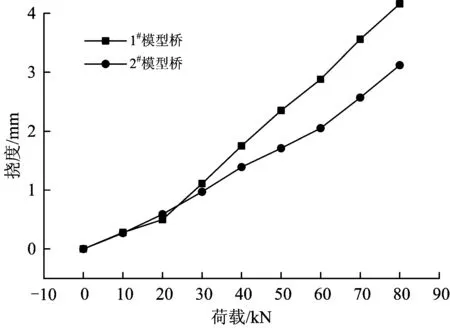
图10 对称荷载作用下1#和2#模型桥中跨跨中截面挠度
由图10和图11可知:在0~80 kN对称荷载和偏载作用下,模型中跨跨中截面的位移均随荷载的增大而增大,且呈线性变化,说明模型处于弹性状态;在同一级荷载作用下,各截面挠度值均是1#模型桥大于2#模型桥,说明波形钢腹板箱梁增设内衬混凝土可使波形钢腹板箱梁的抗弯刚度增加;同级别荷载时,偏载作用下偏载一侧的挠度明显大于对称荷载作用下同一点的挠度。

图11 偏载作用下1#和2#模型中跨跨中截面挠度
相关研究表明,桥梁的刚性扭转和畸变效应是由活载的偏载产生,一般用偏载系数表示,偏载系数定义为偏载作用下偏载侧的挠度与对称荷载作用下该点挠度的比值,根据实测数据计算得到的1#和2#模型桥中跨跨中截面偏载系数见表1。
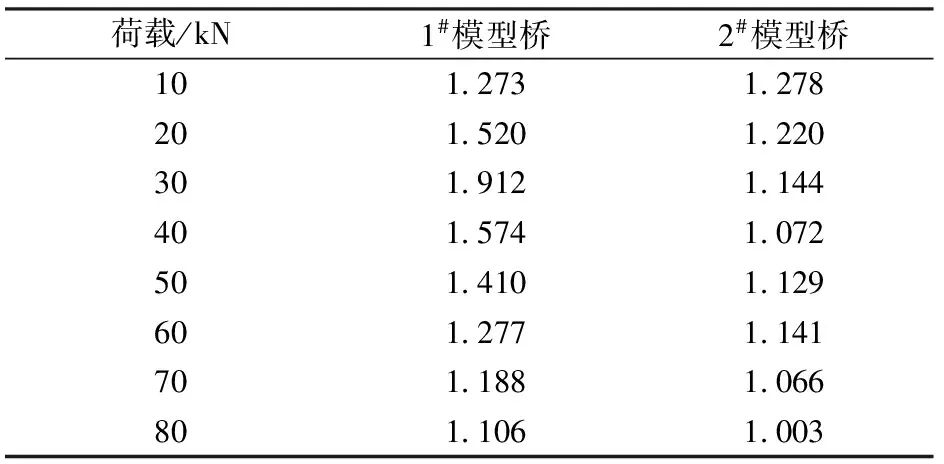
表1 不同荷载作用下1#和2#模型桥偏载系数
由表1可以看出,在相同荷载作用下,1#模型桥的偏载系数大于2#模型桥;同一模型梁,偏载系数随荷载的增大而增大。这说明增加内衬混凝土能够提高波形钢腹板箱梁的扭转刚度。
箱梁在对称荷载作用下,只产生弯曲,而在偏心荷载作用下,在发生弯曲的同时还会发生刚性扭转和畸变。通常因为扭转与畸变之间相互耦合,所以将扭转和畸变作为一项指标进行处理。为了显示箱梁的扭转和畸变效应,将弯曲应力扣除,所得应力为刚性扭转和畸变的综合翘曲应力。
根据实测中跨跨中底板上偏载一侧测点的应变数据,用计算所得偏载作用下产生的应力减去对称荷载作用下产生的应力,得到该测点处的综合翘曲应力。不同荷载作用下中跨跨中底板偏载侧测点后翘曲应力实测值见表2。
表2不同荷载作用下1#和2#模型桥中跨跨中底板偏载侧测点的翘曲应力实测值
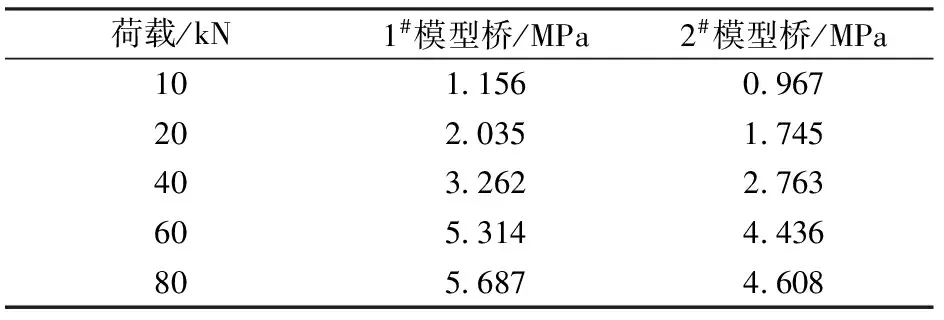
荷载/kN1#模型桥/MPa2#模型桥/MPa101 1560 967202 0351 745403 2622 763605 3144 436805 6874 608
由表2可知:在不同荷载作用下,1#模型桥中跨跨中底板偏载侧测点的实测翘曲应力大于2#模型桥;同一模型桥梁,随着荷载的增大,翘曲应力随之增大。这说明,内衬混凝土的设置对翘曲效应有抑制作用,荷载越大,翘曲效应越显著。
3 模型桥有限元模型的建立及验证
3.1 有限元模型的建立
根据试验梁模型的实际尺寸,利用有限元软件Midas Civil建立2#模型桥的三维实体有限元模型,如图12所示。建模过程中,波形钢腹板采用板单元,混凝土采用实体单元。由于试验桥墩底与基础采用固结,梁墩之间用钢构件连接,边跨两端用橡胶支座支撑,所以有限元模型中约束桥墩底部全部自由度,梁墩采用共节点模拟,边跨边界不约束,内衬混凝土和钢腹板的连接在有限元中采用共节点模拟。
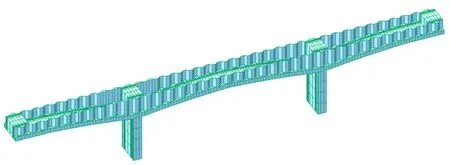
图12 2#模型桥实体有限元模型示意图
3.2 有限元模型验证
3.2.1挠度的有限元结果与试验结果对比
2#模型桥在对称荷载作用下其中跨跨中截面挠度的实测值与有限元计算值如图13所示。
由图13可知:当加载范围为0~80 kN时,2#模型桥的实测值与有限元计算值相差3.5%~5.0%,说明有限元计算结果能反映箱梁挠度的变化趋势,而且精度较高。
3.2.2纵向应力的有限元结果与试验结果对比
2#模型桥在对称荷载作用下其中跨跨中截面偏载一侧底板测点处应力的实测值与有限元计算值如图14所示。
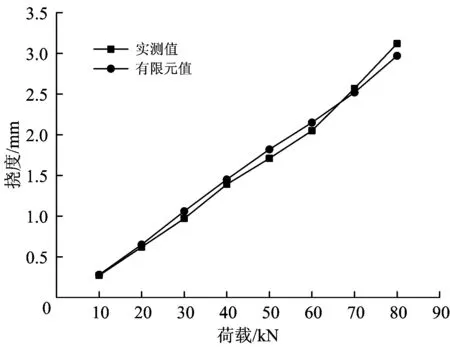
图13 2#模型桥荷载—挠度曲线
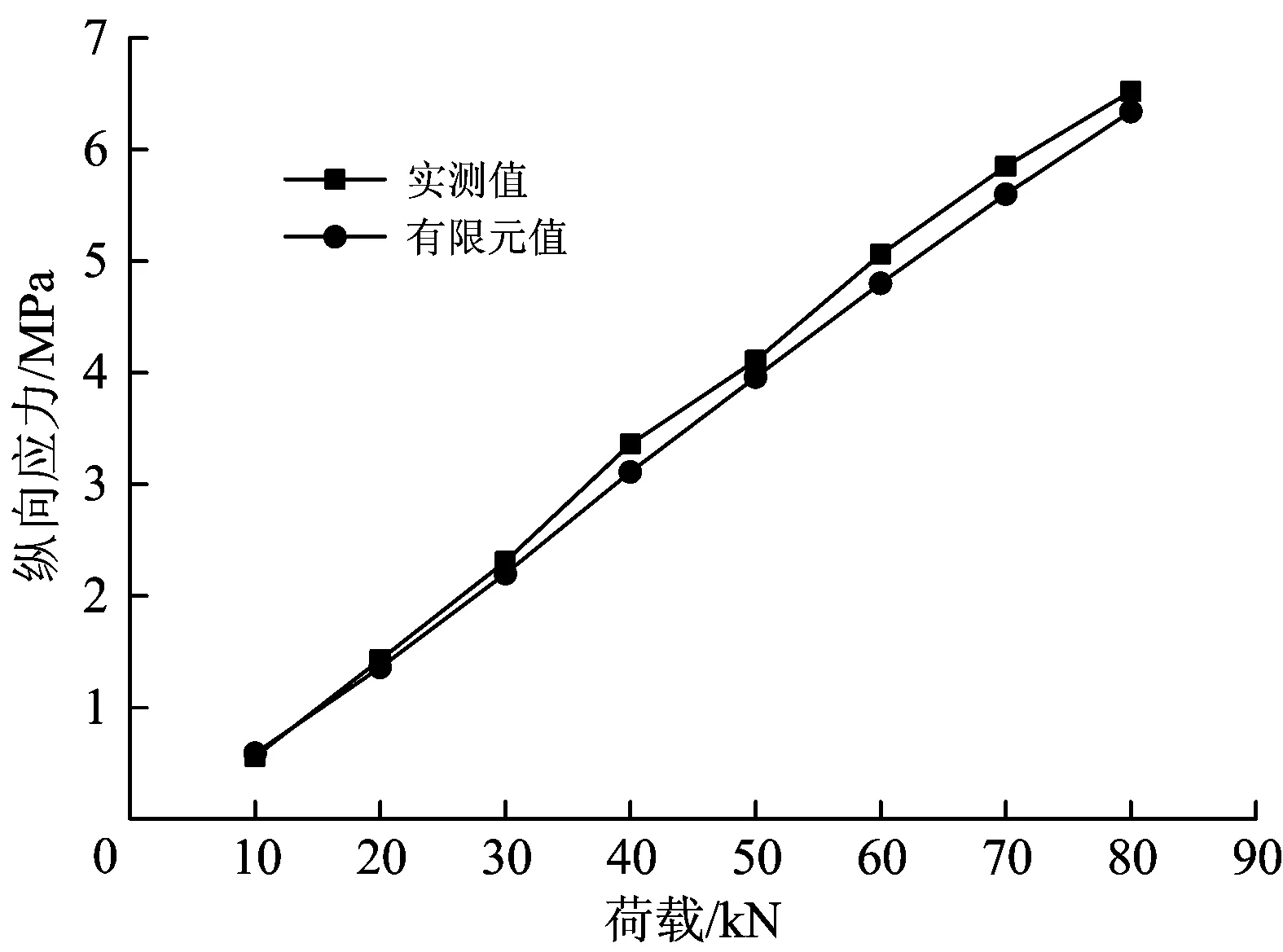
图14 2#模型桥荷载—纵向应力曲线
由图14可知:当加载范围为0~80 kN时,2#模型桥的实测值与有限元值相差3.6%~5.3%,说明有限元值计算结果反映了箱梁纵向应力的变化趋势,精度较高。
因此可以用本文建立的有限元模型进一步分析内衬混凝土几何参数变化对箱梁扭转与畸变的影响。
4 内衬混凝土几何参数变化对扭转和畸变的影响
《公路波形钢腹板预应力混凝土箱梁桥设计规范(河南省地方标准)》[16]规定:当波形钢腹板刚构桥梁跨度较大时,宜在桥墩台顶横隔梁外一定范围内采用波形钢腹板内衬混凝土的组合结构形式,且内衬混凝土厚度不宜小于200 mm。结合规范规定并考虑到试验梁以1∶10的比例尺寸设计,故内衬混凝土最小厚度宜大于20 mm。内衬混凝土最重要的2个参数是长度l和厚度t。
4.1 内衬混凝土厚度的影响
取内衬混凝土长度l为512.5 mm,厚度t依次为20,30,40和50 mm,波形钢腹板箱梁截面形式保持不变。在进行有限元分析时,假定波形钢腹板箱梁的顶板、底板与波形钢腹板连接完好,不产生相对滑移现象;波形钢腹板在受力过程中不发生屈曲现象;不考虑波形钢腹板和混凝土的非线性影响。
4.1.1偏载效应分析
当荷载为80 kN时,在对称荷载和偏心荷载作用下2#模型桥中跨跨中截面的挠度以及偏载系数见表3。
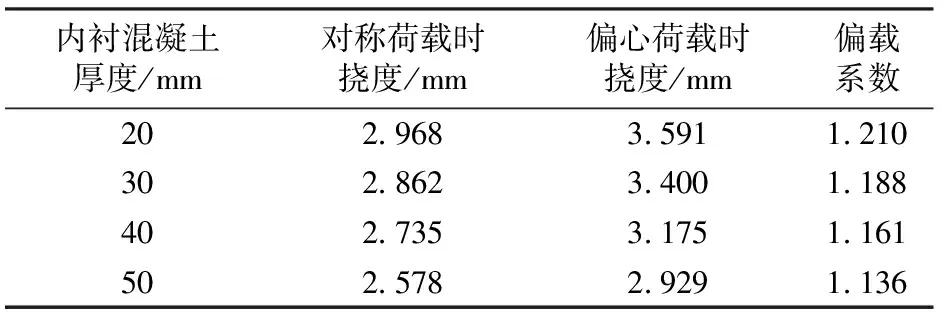
表3 中跨跨中截面挠度与内衬混凝土厚度的关系
由表3可知:2#模型桥中跨跨中截面的偏载系数随内衬混凝土最小厚度的增加而减小,这说明,增加内衬混凝土的最小厚度,使箱梁截面的扭转刚度增大,会对波形钢腹板箱梁截面的扭转起到抑制作用,且这种抑制作用随内衬混凝土厚度的增加而逐渐增大。
4.1.2纵向翘曲效应分析
当荷载为80 kN时,2#模型桥中跨跨中截面和中跨1/4截面偏心荷载一侧底板测点处的纵向应力与内衬混凝土厚度的关系如图15和图16所示。
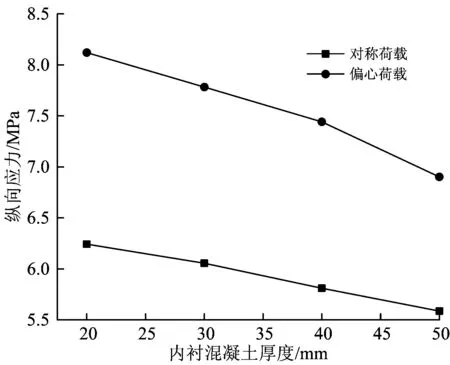
图15 中跨跨中截面纵向应力与内衬混凝土厚度关系
由图15和图16可知:无论在对称荷载还是在偏心荷载作用下,随着内衬混凝土厚度的增加,2#模型桥中跨跨中截面和中跨1/4截面箱梁底板的纵向应力均呈现减小趋势,在偏心荷载作用下中跨1/4截面的纵向应力的减小趋势较明显。
2个截面偏心荷载一侧底板测点处的纵向翘曲应力与内衬混凝土厚度的关系见表4。

图16中跨1/4截面底板纵向应力与内衬混凝土厚度的关系
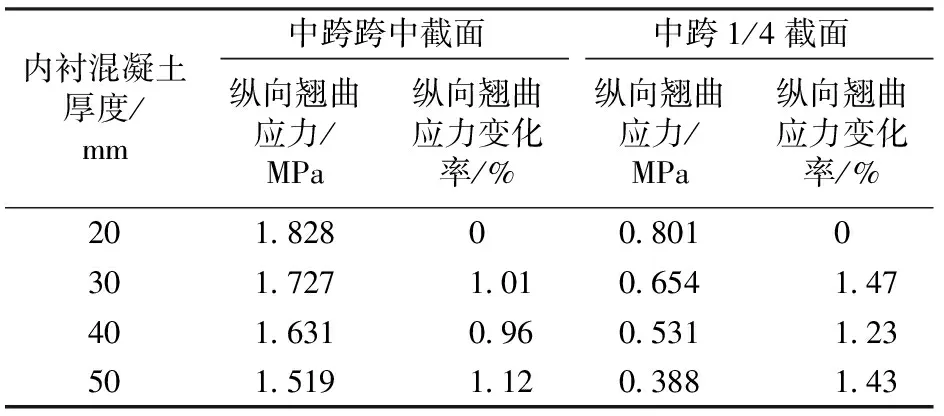
表4 纵向翘曲应力与内衬混凝土厚度的关系
由表4可知:中跨跨中截面和中跨1/4截面的纵向翘曲应力均随内衬混凝土厚度的增加而减小,中跨1/4截面的减小趋势比中跨跨中截面的显著。这说明纵向翘曲应力减小趋势与观测截面距内衬混凝土的设置位置有关,观测截面距内衬混凝土设置位置越近,纵向翘曲应力减小的趋势越明显。
4.2 内衬混凝土纵桥向长度的影响
墩上横隔板两侧内衬混凝土厚度保持20 mm不变,纵桥向长度依次取为225,450,675和900 mm,采用有限元模型对其进行计算分析。
4.2.1偏载效应分析
当荷载为80 kN时,在对称荷载和偏心荷载作用下2#模型桥中跨跨中截面的挠度以及偏载系数见表5。
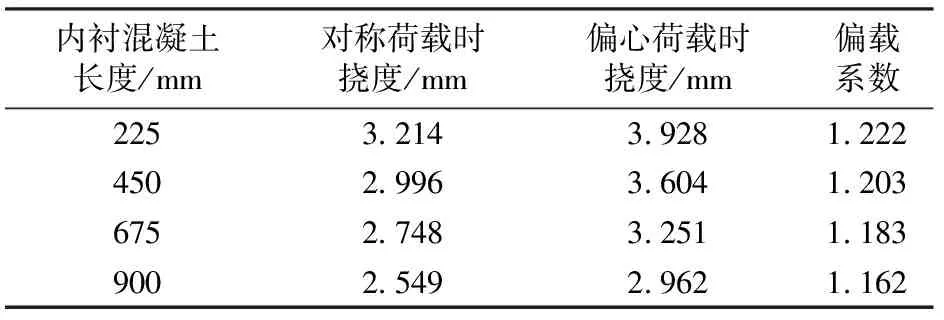
表5 中跨跨中截面挠度与内衬混凝土长度的关系
由表5可以看出:2#模型桥中跨跨中截面的偏载系数随内衬混凝土长度的增加而减小。这说明,增加内衬混凝土长度,使箱梁截面的扭转刚度增大,可以对波形钢腹板箱梁截面的扭转起到抑制作用,且这种抑制作用随内衬混凝土纵桥向长度的增加而逐渐增大。
4.2.2纵向翘曲效应分析
在80 kN对称荷载和偏心荷载作用下,2#模型桥中跨跨中截面和中跨1/4截面偏心荷载一侧底板测点处的纵向应力与内衬混凝土长度的关系如图17和图18所示。
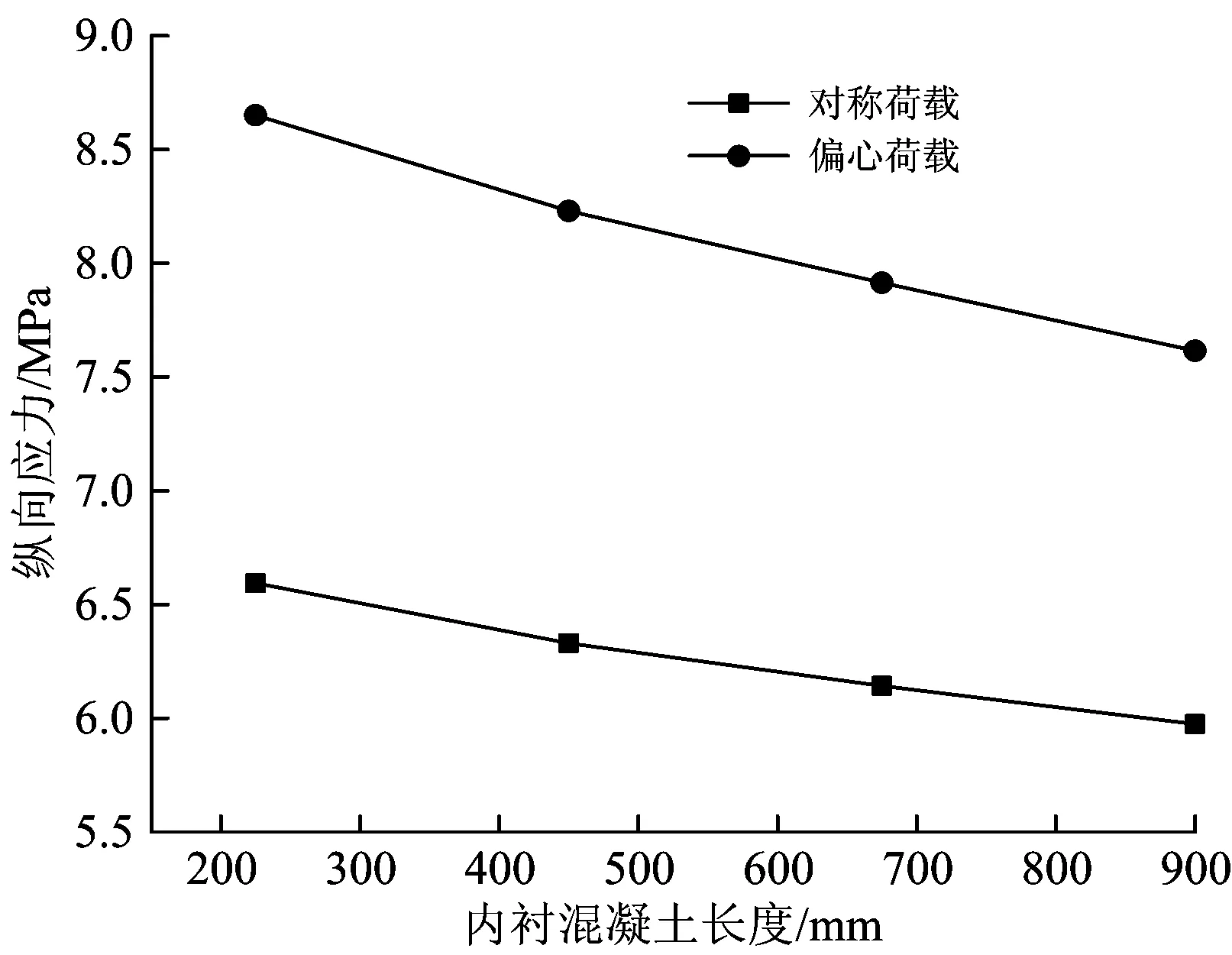
图17中跨跨中截面纵向应力与内衬混凝土长度的关系
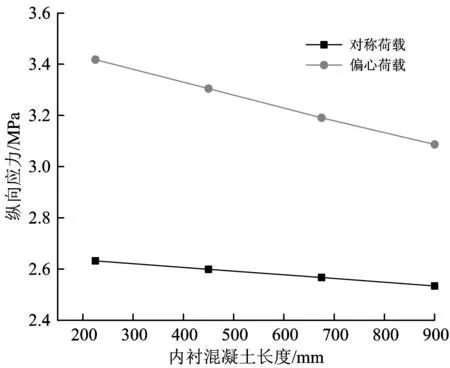
图18中跨1/4截面底板测点纵向应力与内衬混凝土长度的关系
由图17和图18可知:无论在对称荷载还是在偏心荷载作用下,随着内衬混凝土长度的增加,2#模型桥中跨跨中截面和中跨1/4截面箱梁底板的纵向应力均呈现减小趋势,在偏心荷载作用下中跨1/4截面的纵向应力的减小趋势较明显。
2个截面的偏心荷载一侧底板测点处的纵向翘曲应力与内衬混凝土长度关系见表6。
由表6可知,中跨跨中截面和中跨1/4截面的纵向翘曲应力均随内衬混凝土长度的增加而减小,而中跨1/4截面的减小趋势比中跨跨中截面显著。同样说明纵向翘曲应力减小的趋势与观测截面距内衬混凝土的设置位置有关,观测截面距内衬混凝土设置位置越近,纵向翘曲应力减小的趋势越明显。
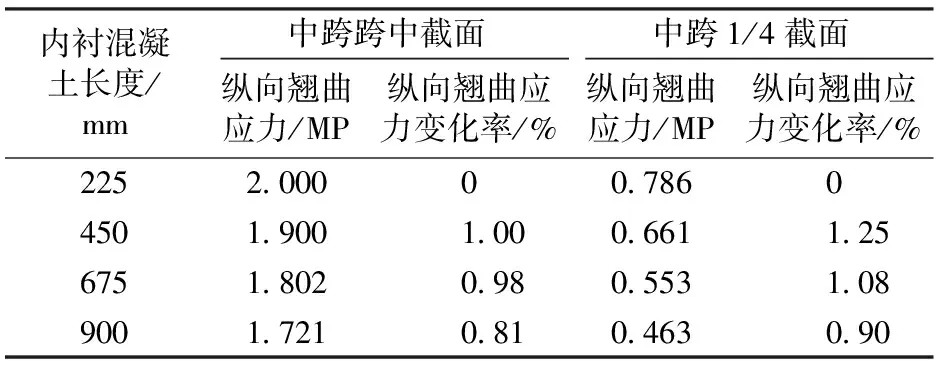
表6 纵向翘曲应力与内衬混凝土长度的关系
4.3 内衬混凝土设置方案的优化
保持内衬混凝土的体积为4.455×106mm3,分别改变内衬混凝土的厚度和长度,得到表7所示5种布置方案,通过分析不同布置方案对桥梁扭转和畸变的影响,进行内衬混凝土布置方案优化。
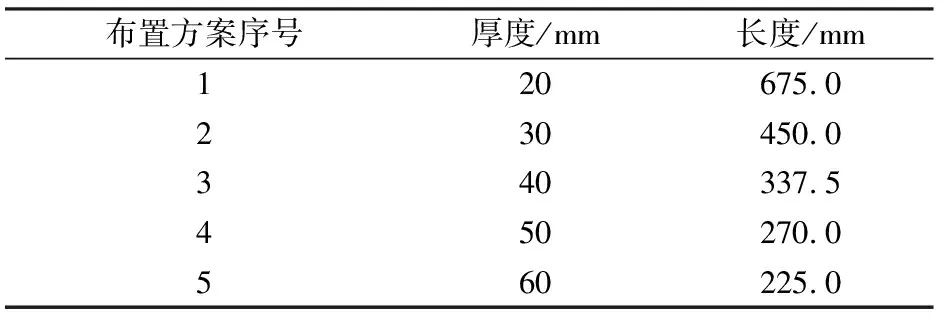
表7 内衬混凝土布置方案
4.3.1偏载效应分析
在80 kN对称荷载和偏心荷载作用下,采用不同内衬混凝土布置方案的2#模型桥中跨跨中截面的挠度以及偏载系数见表8。
表8不同内衬混凝土布置方案下中跨跨中截面的挠度与偏载系数
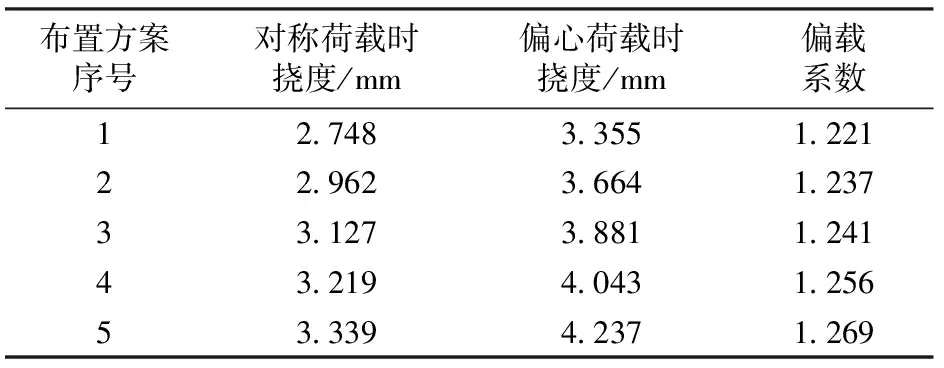
布置方案序号对称荷载时挠度/mm偏心荷载时挠度/mm偏载系数12 7483 3551 22122 9623 6641 23733 1273 8811 24143 2194 0431 25653 3394 2371 269
由表8可以看出:在对称荷载和偏心荷载作用下,当内衬混凝土的体积恒定时,随着内衬混凝土厚度的增加和长度的减小,中跨跨中截面的挠度以及偏载系数均呈增大趋势。这说明,内衬混凝土长度增加引起的箱梁截面抗弯和抗扭刚度的增大值大于厚度增加引起的增大值,从而导致相同体积混凝土的情况下,内衬混凝土厚度增大时桥梁跨中截面的挠度和偏载系数均较大。
4.3.2纵向翘曲效应分析
在80 kN对称荷载和偏心荷载作用下,2#模型桥中跨跨中截面和中跨1/4截面偏心荷载一侧底板测点处的纵向应力与内衬混凝土上布置方案的关系如图19和图20所示。

图19中跨跨中截面底板测点处纵向应力与内衬混凝土布置方案的关系
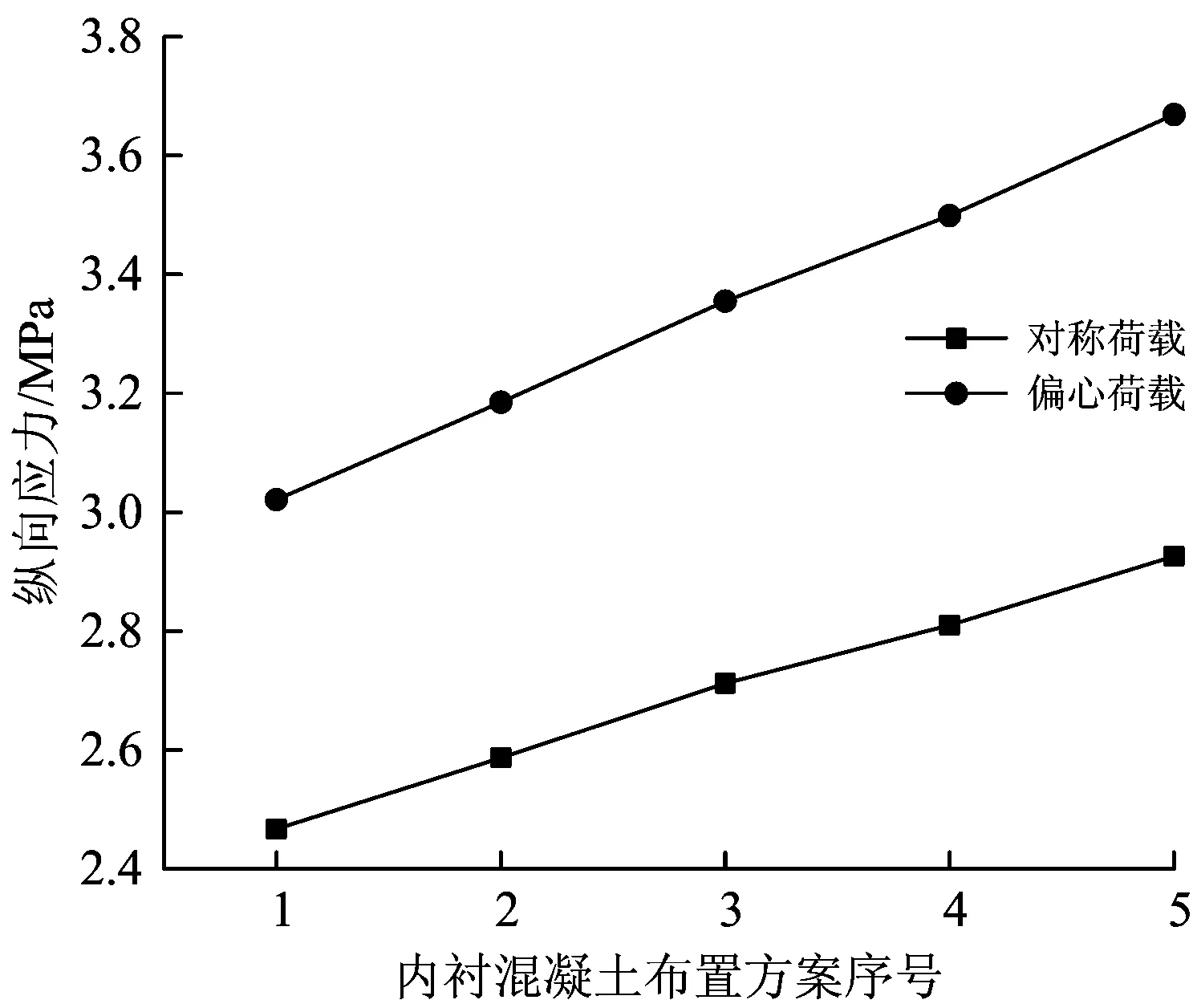
图20中跨1/4截面底板测点处纵向应力与内衬混凝土布置方案的关系
由图19和图20可知:无论在对称荷载还是在偏心荷载作用下,当内衬混凝土体积相同时,随着内衬混凝土厚度的增加,2#模型桥中跨跨中截面和中跨1/4截面箱梁底板的纵向应力均呈现增大趋势。
2个截面偏心荷载一侧底板测点处的纵向翘曲应力与内衬混凝土布置方案的关系见表9。
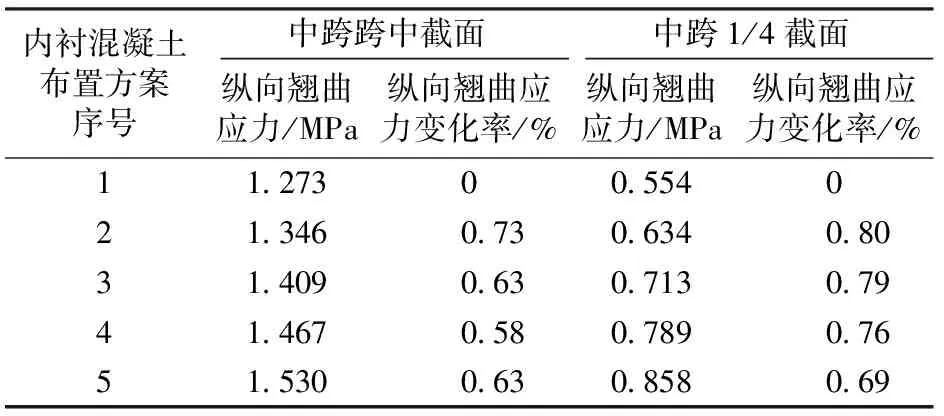
表9 纵向翘曲应力与内衬混凝土布置方案的关系
由表9可知:在内衬混凝土体积相同的情况下,中跨跨中截面和中跨1/4截面偏载一侧底板测点处的纵向翘曲应力均随内衬混凝土最小厚度的增加而增大,中跨1/4截面的增大趋势比中跨跨中截面显著。这说明在内衬混凝土体积恒定的情况下,纵向翘曲应力增大的趋势与观测截面距内衬混凝土的设置位置有关,观测截面距内衬混凝土设置位置越近,纵向翘曲应力增大的趋势越明显。
5 结 论
(1)通过在波形钢腹板箱梁内侧增设内衬混凝土,使得波形钢腹板刚构桥的抗弯刚度和抗扭刚度均增加,内衬混凝土与波形钢腹板共同受力改善了偏载效应和纵向翘曲效应。
(2)内衬混凝土长度恒定的条件下,波形钢腹板箱梁的挠度、偏载系数、纵向应力和纵向翘曲应力均随内衬混凝土厚度的增加而减小,观测截面距内衬混凝土设置位置越近,减小趋势越明显。
(3)内衬混凝土厚度恒定的条件下,波形钢腹板箱梁的挠度、偏载系数、纵向应力和纵向翘曲应力均随内衬混凝土长度的增加而减小,观测截面距内衬混凝土设置位置越近,减小趋势越明显。
(4)相同体积条件下,内衬混凝土长度的增加对波形钢腹板箱梁截面抗弯刚度和扭转刚度提高的影响比厚度增加的影响明显。因此在符合规范及施工条件允许的情况下,用相同体积混凝土时应优先考虑设置较长的内衬混凝土,以减小波形钢腹板刚构桥的扭转和畸变。
[1]MO Y L, FAN Y. Torsional Design of Hybrid Concrete Box Girders[J]. Journal of Bridge Engineering, 2006, 11(3): 329-339.
[2]刘海燕. 日本黑部川大桥——首座波形钢腹板铁路桥[J].世界桥梁,2015(3):91-91.
(LIU Haiyan. Kurobegawa Bridge in Japan—the First Railway Bridge with Corrugated Steel Web[J].World Bridges,2015(3):91-91. in Chinese)
[3]文鹏. 铁路预应力波形钢腹板简支T梁桥设计研究[J].铁路标准设计,2012 (11):50-53.
(WEN Peng. Research on the Design of Railway Simply-Supported Prestressed T-Girder Bridge with Corrugated Steel Webs[J].Railway Standard Design,2012(11):50-53. in Chinese)
[4]BROZZETTI J. Design Development of Steel-Concrete Composite Bridges in France. [J]. Journal of Constructional Steel Research,2000, 55(1/2/3): 229-243.
[5]EY Sayed-Ahmed. Behaviour of Steel and (or) Composite Girders with Corrugated Steel Webs[J].Canadian Journal of Civil Engineering, 2001,28(4):656-672.
[6]周绪红,狄谨,游金兰,等.波纹钢腹板预应力混凝土箱梁抗扭性能试验研究[J].哈尔滨工业大学学报,2007,39(增2):150-155.
(ZHOU Xuhong, DI Jin, YOU Jinlan, et al. Experimental Research on Torsional Property of Composite Beam with Corrugated Steel Webs[J]. Journal of Harbin Institute of Technology, 2007,39(Supplement 2):150-155. in Chinese)
[7]狄谨,周绪红,游金兰,等.波纹钢腹板预应力混凝土组合箱梁抗扭性能[J].长安大学学报:自然科学版,2009,29(3):58-63.
(DI Jin, ZHOU Xuhong, YOU Jinlan, et al. Torsional Property of Prestressed Concrete Composite Beam with Corrugated Steel Webs[J].Journal of Chang’an University:Natural Science Edition, 2009,29 (3):58-63. in Chinese)
[8]刘保东,冯文章,任红伟,等. 波纹钢腹板连续刚构桥扭转与畸变的试验研究[J]:中国铁道科学,2015,36(4):40-46.
(LIU Baodong, FENG Wenzhang, REN Hongwei, et al.Experimental Study on Torsion and Distortion of Continuous Rigid Frame Bridge with Corrugated Steel Webs[J].China Railway Science, 2015,36(4):40-46. in Chinese)
[9]李宏江.波形钢腹板箱梁扭转与畸变的试验研究及分析[D].南京:东南大学,2003.
(LI Hongjiang. Experimental Study and Analysis on Torsion and Distortion of Box-Girder with Corrugated Steel Webs[D].Nanjing:Southeast University, 2003. in Chinese)
[10]李宏江,叶见曙,万水,等.波形钢腹板箱梁横隔板间距的研究[J].公路交通科技,2004,21(10):51-54.
(LI Hongjiang. YE Jianshu, WAN Shui, et al. Research on Diaphragm Distance of Box Girder with Corrugated Steel Webs[J]. Journal of Highway and Transportation Research and Development,2004,21(10):51-54. in Chinese)
[11]李宏江,叶见曙,万水,等.波形钢腹板预应力混凝土箱梁的试验研究[J].中国公路学报,2004,17(4):31-36.
(LI Hongjiang,YE Jianshu, WAN Shui, et al. Experimental Research on Prestressed Concrete Box Girder with Corrugated Steel Webs[J]. China Journal of Highway and Transport,2004,17(4):31-36. in Chinese)
[12]NAKAMURA S,NARITA N. Bending and Shear Strengths of Partially Encased Composite I-Girders [J].Journal of Constructional Steel Research, 2003, 59(12):1435-1453.
[13]江越胜,孙天明,仵云飞. 波形钢腹板PC组合箱梁桥内衬混凝土钢混组合段抗剪验算[J].公路,2013, 58(12):91-96.
(JIANG Yuesheng, SUN Tianming, WU Yunfei. Corrugated Steel Web PC Composite Lining Concrete Box Girder Bridge Steel Combined Section Shear Calculation[J]. Highway, 2013, 58(12):91-96. in Chinese)
[14]刘朵,杨丙文,张建东,等. 波形钢腹板组合桥梁内衬混凝土抗剪性能研究[J].世界桥梁,2013, 41(6):72-75.
(LIU Duo, YANG Bingwen, ZHANG Jiandong, et al.Corrugated Steel Web Composite Bridges Lined with Concrete Shear Performance [J]. Bridge World, 2013, 41(6):72-75. in Chinese)
[15]王达磊, 贺君,陈艾荣,等.内衬混凝土波折钢腹板梁抗弯性能试验研究[J]. 同济大学学报:自然科学版,2012,40(9):1312-1317.
(WANG Dalei, HE Jun, CHEN Airong, et al. Experimental Study on Bending Behavior of Concrete-Encased Composite Girder with Corrugated Steel Web[J]. Journal of Tongji University:Natural Science,2012, 40(9):1312-1317. in Chinese)
[16]河南省地方质量监督局.DB 41—2010公路波形钢腹板预应力混凝土箱梁桥设计规范(河南省地方标准)[S].河南:河南省地方质量监督局,2010.
