基于SOM神经网络和复相关系数结合的机床主轴温度测点的优化筛选

王战中， 孙少华

(石家庄铁道大学 机械工程学院，河北 石家庄 050043)

基于SOM神经网络和复相关系数结合的机床主轴温度测点的优化筛选

王战中， 孙少华

(石家庄铁道大学 机械工程学院，河北 石家庄 050043)

提出了基于SOM神经网络和复相关系数相结合的温度测点的优化算法，并应用于SV-48立式加工中心主轴测温点优化筛选。首先，在主轴上模拟布置温度传感器和Z轴位移传感器，在有限元分析的基础上得到了一系列温度和Z轴热位移仿真数据；然后，将温度数据输入到SOM神经网络聚类分组；最后利用复相关程度法将聚类的温度值与主轴Z轴热误差拟合，确定出机床热敏感点。研究结果表明，该方法简明易懂，有效减少了测温点的数量。

SOM神经网络；复相关系数；热敏感点；优化算法

0 引言

高精度是制造业永久的追求目标，被称作“工作母机”的机床承担着提高加工精度的重要使命。研究表明机床主轴的热误差是影响加工精度的关键因素之一[1]。机床热误差补偿技术能将实时采集的温度和热位移数据输入到预测模型中进而预测机床误差[2]。借助温度传感器可以采集温度和热位移数据，温度传感器布置越多越能准确的反映出机床主轴复杂的温度场变化，但会加大热误差测量和计算量，同时增加了投入成本；布置太少又难以准确反映温度场的变化情况，影响热误差补偿模型的精度，所以，温度传感器的布局直接影响到机床热误差补偿效率。温度测点的优化筛选是机床热误差补偿技术研究的侧重点之一[3]。常用的方法(诸如线性回归法、模糊聚类法、神经网络求偏导数法等)选取过程耗时，并且在处理大量样本和多指标的体系时存在一定难度，影响了补偿模型的鲁棒性。

本文通过对SV-48立式加工中心主轴模型的热特性分析，在主轴模型上模拟布置温度传感器和Z轴位移传感器，提出采用SOM神经网络对测温点样本数据聚类分组，再利用复决定系数判决测温点与热位移间拟合度，从各组变量中选取典型变量作为最终的热敏感点。

1 测点布置

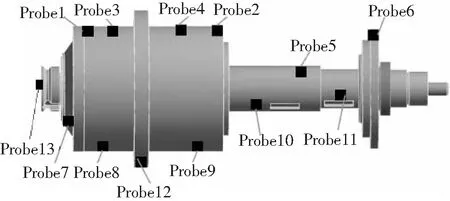
图1 传感器布置示意图

测点布置，即温度传感器和位移传感器的布置，需要根据实际情况综合考虑。根据文献[4]提出的测点布置策略，结合对SV-48立式加工中心主轴结构分析、热特性理论分析和有限元分析结果，在机床主轴上模拟布置12个温度传感器(Probe 1～Probe12)和1个Z轴位移传感器(Probe 13)，布置示意图见图1。

2 测温点优化筛选

借助ANSYS Workbench有限元分析软件，基于示意图1测点的布置，模拟主轴在转速8 000下工作7 200 s。每隔300 s提取一次数据，整理各测温点和Z轴热位移的仿真结果分别如图2、图3所示。

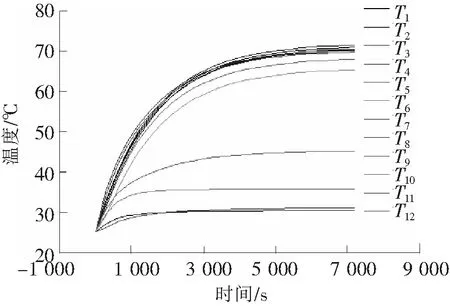
图2 各测温点温度值仿真结果

图3 Z轴热位移仿真结果

2.1 基于SOM神经网络的测温点的聚类分析

聚类[5]分析是直接比较各事物之间的性质，将性质相近的归为一类，将性质差别较大的归入不同的类。SOM神经网络采用的算法属于无导师的聚类法，能将任意维数的输入模式在竞争层映射成一维或二维离散图，同时保持拓扑结构不变。其具体学习过程如下：

(1)初始化。对输出层各权向量赋小随机数并做归一化处理，得到权值Wj，j=1,2,…,m；建立初始优胜领域Nj*(0)；学习率η赋初始值。

(3)寻求获胜节点计算Xp·Wj，从中选出点积最大的获胜节点。

(4)定义优胜领域Nj*(t)。以j*为中心，确定t时刻的权值调整域，Nj*(t)在训练过程中会随训练时间逐渐收缩。

(6)结束检查。检查学习率是否衰减到零或某个预定的正小数。

本节聚类分析的目的就是将图2中T1～T12的共12组数据分类。使用newsom函数创建SOM神经网络，其格式为net=newsom(PR, [D1,D2,^],TFCN,DFCN,OLR,OSTEPS,TLR,TND)。本节中使用的TFCN、DFCN、OLR、OSTEPS、TLR、TND均采用缺省值。初始化init设置的初始化权值是自动完成的，用随机数设置输入层和竞争层之间权值的初始值。设置训练train次数分别为50、100、1 000、2 000次，便于对运算结果进行比较。

将T1～T12组测温点数据从ANSYS Workbench中以.xls格式导出，文件命名为’shuju’，作为训练样本数据，输入到SOM神经网络中，在默认初始化权值下，对训练样本进行多次训练。测温点数据再次输入到训练好的模型中，在sim函数下，得到的聚类结果如表1所示，数值相同的为一类。

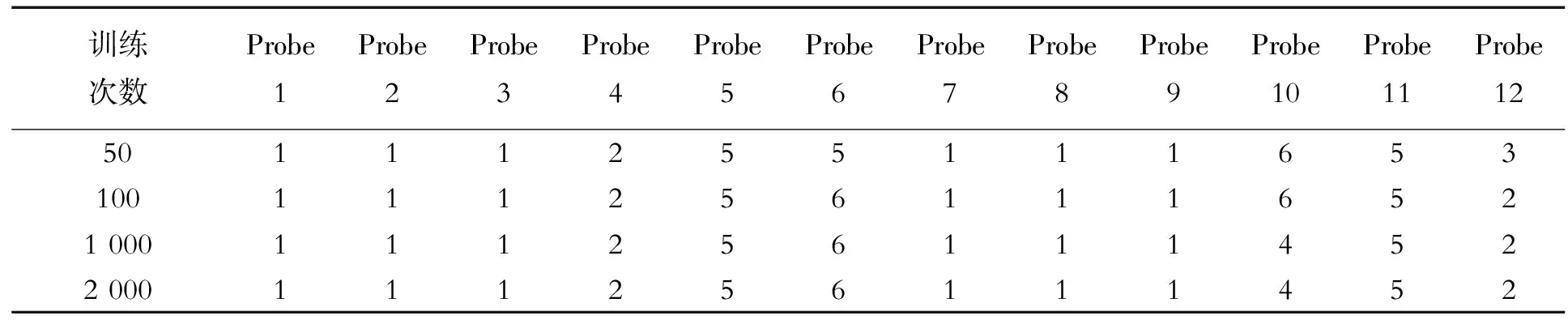
表1 温度值聚类结果

结果表明，当运算次数为50、1 000、2 000次时，聚类为5类；当运算次数为100次时，聚类为4类。综合实际情况，最终将温度值聚类为5类：T1=[T1,T2,T3,T7,T8,T9]；T2=[T4,T12]；T3=[T5,T11]；T4=[T6]；T5=[T10]。

2.2 基于复决定系数的最优测温点的选取

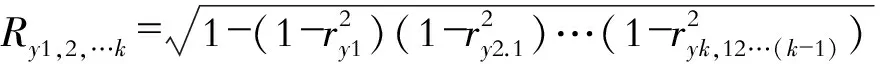
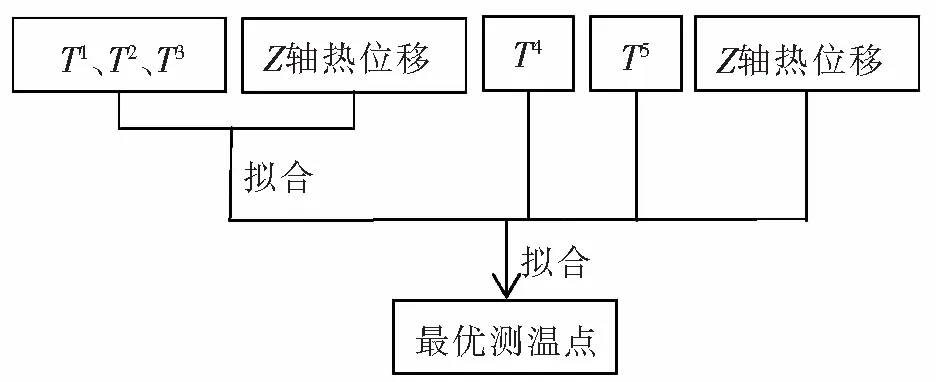
图4 最优测温点分析流程图

利用SPSS软件中的复相关程度法将聚类的温度值与主轴Z轴热误差拟合，根据拟合程度对温度值进行取舍。本节将2.1中的聚类结果以EXCEL格式保存。对T1、T2、T3数据分别进行拟合分析，将3类样本得到的拟合结果与T4、T5组合作为新一类样本T0与主轴Z轴热误差拟合，最终得到最优测温点。SPSS分析流程如图4所示。

以T1类数据为例，SPSS拟合分析过程如下所示：

使用SPSS19.0，选择“分析”中的“回归”进行线性拟合。因变量设置为主轴Z轴热误差，自变量为T1=[T1,T2,T3,T7,T8,T9]中的6组数据。线性回归方法设置为逐步回归，即每次只纳入或者移除一个变量进入模型，其他按默认设置。结果预测变量为T7，此时负相关系数R为1，标准估计的误差为6.498 423 8×10-8。已排除的变量如表2所示。

表2 已排除的变量

注：预测变量为T7，因变量为Y。

最终计算结果显示T1类样本最优测温点为T7。对T2=[T4,T12]、T3=[T5,T11]按照同样的方法计算，分别得到最优测温点T4、T12，T11。重新组合各类样本最优测温点，即T0=[T7,T4,T12,T11,T6,T10]。对T0类数据拟合分析，得到最终优化测温点为T4,T7,T10。

3 结束语

本文依托有限元瞬态热-结构耦合分析，在主轴上模拟布置12个温度传感器和1个位移传感器，每隔300 s收集一次温度和位移数据，将最终得到的12组温度数据和1组Z轴位移数据作为样本。详细阐述了使用SOM神经网络聚类和复相关系数优化相结合的方法优化筛选温度测点的过程，最终将温度测点数量降到3组。结果表明该方法简明易懂，有效减少了测温点的数量。

[1]窦小龙, 杨建国. 温度测量点优化在机床主轴热误差建模中的应用[J]. 航空机密制造技术, 2003, 39(4): 33-36.

[2]张成新, 高峰, 李艳. 基于实时反馈的机床热误差在线补偿模型[J]. 中国机械工程, 2015(3):361-364.

[3]陈瑜婷. 数控机床热误差补偿中测温点优化研究[D]. 武汉：武汉理工大学，2014.

[4]黎新齐. 铣削加工中心主轴组件热特性的研究[D]. 兰州：兰州理工大学，2008.

[5]张建萍, 刘希玉. 基于聚类分析的K-means算法研究及应用[J]. 计算机应用研究, 2007，24(5):166-168.

Optimal Selection of Temperature Measuring Points for Spindle of Machine Tool Based on Method of Combining SOM Neural Network and Multiple Correlation Coefficient

Wang Zhanzhong， Sun Shaohua

(School of Mechanical Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China)

A novel optimization algorithm based on method of combining the SOM neural network and multiple correlation coefficient for identifying temperature measuring points is presented, which is applied to the main spindle of SV-48 vertical machining center. Firstly, a series of temperature sensors and Z-direction displacement sensors are placed on the spindle in simulation state and a series of temperature simulation data and Z-direction thermal displacement simulation data are obtained; A series of temperature simulation data are then clustered by SOM neural network. Finally, the temperature value after clustering and the spindle Z-direction thermal error are fitted by using complex correlation method, then, the thermal sensitive points of the machine tool are determined. The result shows that the method is clear and easy to understand, and effectively reduces the number of temperature measurement points.

SOM neural network;multiple correlation coefficient;the thermal sensitive points;optimization algorithm

2016-01-30 责任编辑:刘宪福

10.13319/j.cnki.sjztddxxbzrb.2017.01.18

王战中(1969-)，男，副教授，博士，主要从事机器人技术与应用、数控技术及数字化制造的研究。E-mail:sjzwzz@163.com

TG502.15

A

2095-0373(2017)01-0095-04

王战中，孙少华.基于SOM神经网络和复相关系数结合的机床主轴温度测点的优化筛选[J].石家庄铁道大学学报:自然科学版,2017,30(1):95-98.