双稳态随机共振系统参数调整优化研究

杨红娜， 郝如江， 梁建华

(1.石家庄铁道大学 机械工程学院,河北 石家庄 050043;2.北京铁路局 北京机务段,北京 100000)

双稳态随机共振系统参数调整优化研究

杨红娜1， 郝如江1， 梁建华2

(1.石家庄铁道大学 机械工程学院,河北 石家庄 050043;2.北京铁路局 北京机务段,北京 100000)

双稳态随机共振系统处理工程实际信号，需要调节的参数多，很难确定参数的调节方向以快速达到共振状态。文章从势函数角度，探讨了势函数的形状特征对双稳态随机共振系统输出特性的影响。提出了一种基于势函数的参数控制方法，将系统的可调参数降为1个，减少了参数调节的冗余度，且可以在小参数的情况下突破近似绝热条件，使系统用于高频信号检测。经过仿真和实验采集数据验证，该方法简单可行，具有一定的应用价值。

随机共振；势函数；参数控制

0 引言

Benzi1等人在1981研究地球气候规律时提出随机共振(SR)的概念[1]。经过几十年的研究表明，随机共振在放大微弱周期信号方面具有明显优势，尤其是双稳态随机共振模型，已经成为众多学者研究机械故障信号的典型模型[2-5]。双稳态随机共振系统受近似绝热条件的限制，只能处理1Hz以下的低频信号，在工程实际中应用受限。为了突破近似绝热条件的限制，一般采用参数调节法使系统适应不同频率的要求[6]，常用的参数调节法有归一化、变步长等。双稳态SR系统本身有两个参数(a、b),由于实际信号的复杂性，直接给定的参数往往不能使系统稳定输出。因此，这些方法虽然能够应用于实际信号的处理，但在具体应用中，存在的突出问题是很难确定参数的调整方向，以尽快达到随机共振状态，且最终参数的数量级会差别很大[7]。减少系统需要调节参数的数量，可以降低参数调节的难度，但是固定参数a(或b)，调节另一参量b(或a)很难使系统稳定输出。

不同的参数组合对应不同的势垒高度和势阱间距的配合，文献[8]研究了非侵入型随机共振的方法，降低势垒高度，获得了更好的输出信噪比。文献[9]用外加信号的方式，强行改变势函数的势垒高度，提高了输出信噪比。这些研究表明，势垒高度对系统的输出具有一定的指导意义。为了更加深入地研究双稳态SR系统的输出特性，探究降低参数冗余度的途径，文章从势函数的角度出发，对双稳态SR系统的输出特性进行了系统研究。提出了一种基于势函数的参数控制方法，该方法不仅可以将系统需要调节的参数降为1个，而且可以在小参数的情况下突破近似绝热条件。将研究成果用于齿轮早期裂纹故障信息提取，结果表明该方法简单可行。

1 势函数模型

受外力和噪声共同作用的双稳态SR模型可以由Langevin方程描述，即

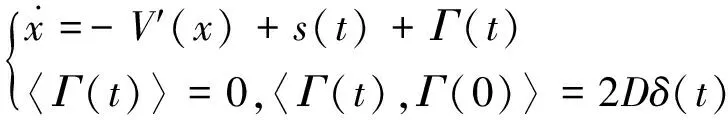
(1)

式中，V(x)为非线性双稳态势函数，且

(2)

式中，s(t)为外力；Γ(t)是强度为D、均值为0的高斯白噪声。

图1 势函数

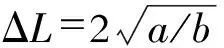
一般情况下，为了使系统能有较好的输出，可以调节a、b的值来降低势垒ΔV高度[8-10]，但是a、b同时也是势阱间距ΔL的参数，在调节势垒高度时会间接改变ΔL的值。为了定量研究ΔV和ΔL分别对系统输出的影响，我们引入信噪比的概念，定义

(3)

式中，A为有用信号的幅值；D为噪声强度。

2 仿真分析

2.1 低频信号分析

取仿真信号x=0.5sin(2π×0.1×t)+5×randn(t)，特征频率0.1 Hz，幅值A=0.5，采样频率20 Hz，采样点数为2 000，采用4阶龙格库塔算法进行数值计算。图2为分析所用仿真信号时域波形。

势阱间距ΔL可以做如下变换

(4)

令ΔV=a2/4b为定值，分别取势垒高度ΔV为0.025、0.25、0.5、1.5、2、2.5，调节参数a(势阱间距ΔL)，系统输出的信噪比变化如图3所示。

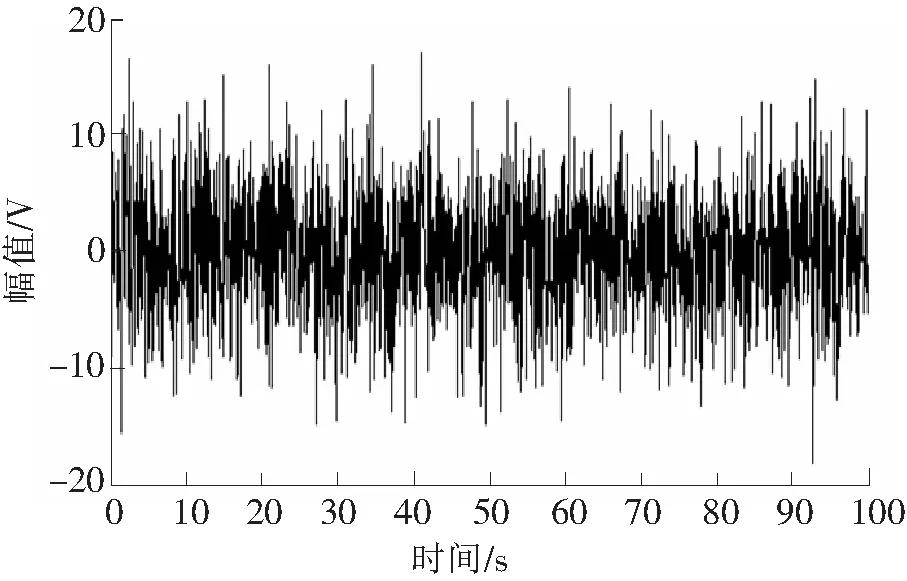
图2 仿真信号

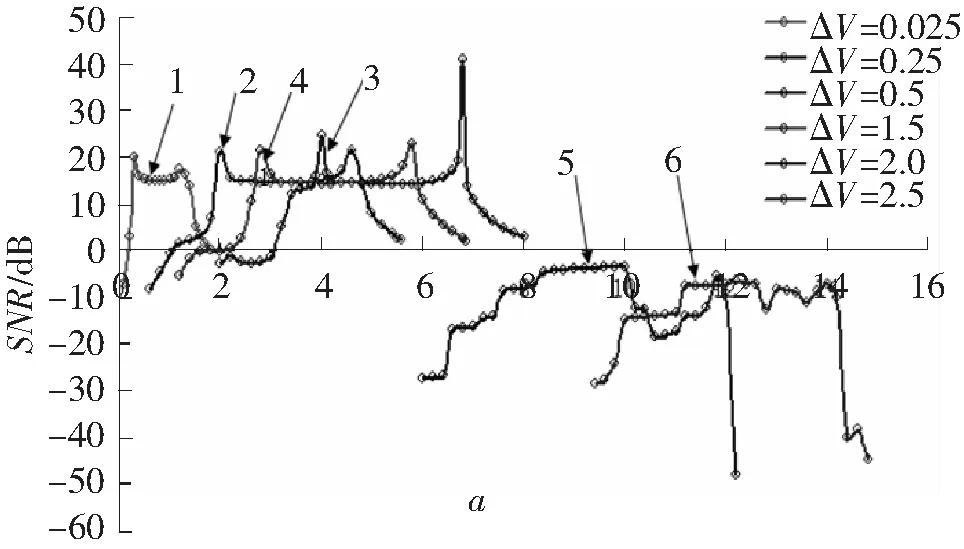
图3 系统输出特性曲线

对比6条曲线，随着势垒高度ΔV的增大，前4条曲线保留了较好的相似性。随着参数a的增大(ΔL变小)，输出信号信噪比首先快速升高，出现一个尖峰，然后趋于稳定，稳定值在15dB左右，在稳定区的末端也会出现一个尖峰，然后信噪比迅速降低，降到一定值后发散，丧失稳定性。(说明：由于曲线在两端的峰值区，信噪比值变化剧烈，图中曲线的峰值大小不代表该峰值区的最大值。本文以两峰值区中间的稳定段，作为整条曲线优劣的评价标准。)曲线5、6是势垒高度ΔV=2和ΔV=2.5时的输出信噪比变化曲线，随着参数a的增大(ΔL变小)，两条曲线的整体变化趋势都有一个先增后减的过程，但是最佳信噪比值变低，对比前4条曲线，这2条曲线丧失了前者的变化规律和输出特性，不具有应用价值。因此可以得出结论，势垒高度ΔL合适的情况下，输出信号的信噪比值与势垒高度的具体值大小关系不大，其输出特性直接决定于势阱间距ΔL(a)的大小，但是当势垒高度过大时，粒子没有办法完成跃迁，SR系统丧失应用特性。

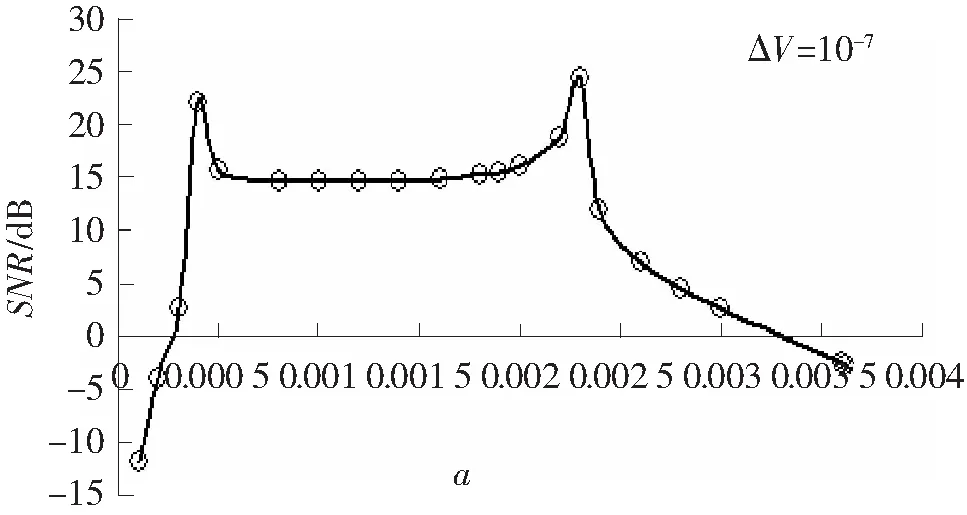
图4 系统在势垒高度很小时的输出曲线

势垒高度过大会使SR系统输出特性变差，但是在图3中并没有体现出势垒高度过小时SR系统的输出特性，猜想在势垒高度非常低的时候依然可以得到较好的信噪比值。为验证猜想，令ΔV=a2/4b=10-7，调节参数a，得到图4。

由图4可知，在势垒高度ΔV=10-7时，稳定区信噪比为15左右，曲线变化趋势与图3中曲线1、2、3、4相似，保留了SR系统的良好输出特性。

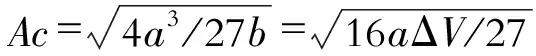
2.2 高频信号分析

在上一节中提出了控制势垒高度ΔV调节势阱间距ΔL的参数调节方法，并探讨了这种参数调节方法的输出特性，得出势垒高度非常小时(ΔV=10-7)并不影响系统的输出特性，反而势垒高度较大时容易出现低信噪比输出的情况。因此，本文提出在用SR系统处理未知信号时，可将系统的势垒高度ΔV控制在较小的值，保证参数调节的有效性。

为了验证该参数控制方法对高频信号同样适用，取仿真信号x=0.5sin(2π×1 000×t)+5×randn(t)，信号频率f=1kHz，采样频率fs=200kHz，采样点数为2 000。噪声数据与上节分析用噪声相同。

分别取势垒高度ΔV为10-7和1，系统输出信噪比的变化曲线如图5，图6所示。

图5和图6分别为ΔV为10-7和1时的输出信噪比变化曲线，两条曲线变化趋势一致，稳定区幅值在15dB左右，与低频信号处理结果(图3)一致，说明该参数控制方法具有较好的稳定性，可以用于处理高频信号。对比图5和图6参数的取值范围，在势垒高度较小时(图5)，系统输出特性曲线在a轴方向上压缩且向0点偏移。因此，在控制势垒高度较小时，系统可以在小参数的情况下突破近似绝热条件，应用于高频信号检测。

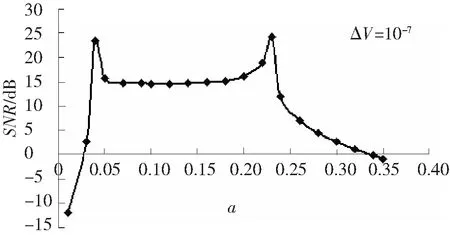
图5 势垒高度为10-7时的输出特性曲线

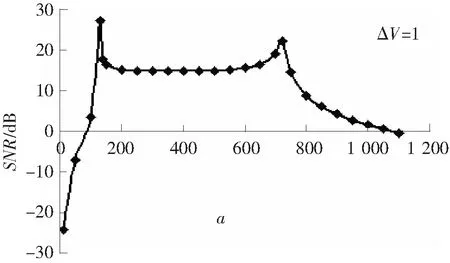
图6 势垒高度为1时的输出特性曲线

3 齿轮箱故障信号分析

本节采用QPZZ-Ⅱ齿轮故障系统，试验台如图7所示。设计模拟了齿轮单齿齿根早期裂纹故障，裂纹深度0.5 mm，电机转频为12.1 Hz，传感器安装在齿轮箱箱体上，采样频率10 kHz，采样时间长度为6.4 s。齿轮齿数及计算得到的大小齿轮的转频如表1所示。

表1 齿轮参数

图7 齿轮箱故障试验台

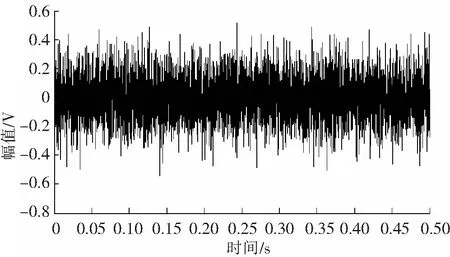
图8 采集信号时域波形

QPZZ-Ⅱ齿轮故障系统为定轴一级传动齿轮箱，由理论分析可知，当其中一个齿轮发生裂纹故障时，采集信号的特征频率即为故障齿轮的转频。但是在工程信号中，特征频率常与较高的机械固有频率发生调制，因此不能直接用随机共振直接加强特征信号。针对这个问题本文将包络解调与随机共振相结合来诊断齿轮箱的早期裂纹故障。首先将采集的信号经过包络解调预处理，得到含有低频特征信号的数据，然后将该数据导入SR系统，采用控制势垒高度调节势阱间距的参数调节方法，令ΔV=10-7，调节参数a=0.3时，系统输出如图9所示。

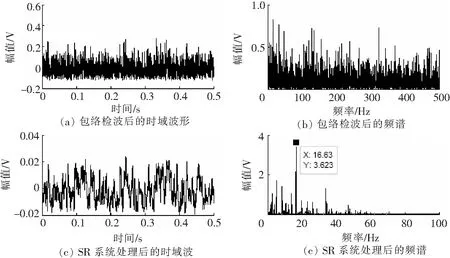
图9 齿轮裂纹信号处理结果图

图9(a)为包络检波后的时域波形，波形杂乱密集，无明显周期成分；图9(b)为图9(a)中信号的频谱图，频率成分复杂，特征频率被淹没，说明该信号特征微弱，单一的包络解调方法对该信号失效；图9(c)SR系统处理后的时域波形，对比图9(a)可知，经SR系统后，信号要清晰很多，规律性初显；图9(d)图9(c)中信号的频谱图，对比图9(b)可知，高频成分明显受到抑制，峰值频率16.63 Hz，与计算故障特征频率16.5 Hz接近，峰值突出。以上检测结果说明，双稳态SR系统采用控制势垒高度的参数调节方法，不仅减少了参数冗余度，而且在在小参数的情况下，成功检测了齿轮的早期裂纹故障信号。

4 结语

本文针对随机共振在工程实用中需要调节的参数多、参数调节方向不明确的问题，系统地研究了双稳SR系统在势函数形状特征控制下系统的响应特性。研究表明：双稳态SR系统稳定与否，不影响系统输出的最佳信噪比；在势垒高度比较低时，系统输出特性曲线在a轴方向上得到压缩。因此，本文提出采用较低的势垒高度控制系统参数，不仅可以降低参数调节的冗余度，而且可以使系统在小参数时突破近似绝热条件，应用于高频信号检测。将研究成果用于齿轮早期裂纹数据的处理验证，结果表明，该方法简单可行。

[1]BenziR,SuteraA,VulpianiA.TheMechanismofStochasticResonance[J].JournalofPhysicsA:MathematicalandGeneral, 1981 ,14 :453-457.

[2]雷亚国,韩冬,林京,等.自适应随机共振新方法及其在故障诊断中的应用[J].机械工程学报,2012,48 (7) :62-67.

[3]郝研,王太勇,万剑,等.基于级联双稳随机共振和多重分形的机械故障诊断方法研究[J].振动与冲击,2012,31 (8) :181-185.

[4]焦尚彬,杨蓉,张青,等.α稳定噪声驱动的非对称双稳随机共振现象[J].物理学报,2015,64 (2) :49-57.

[5]夏均忠,刘远宏,马宗坡,等.基于调制随机共振的微弱信号检测研究[J].振动与冲击,2012,31(3):132-135.

[6]李小龙,冷永刚,范胜波,等.基于非均匀周期采样的随机共振研究[J].振动与冲击，2011,30(12):78-84.

[7]冷永刚,王太勇,郭焱,等. 双稳随机共振参数特性的研究[J].物理学报,2007,56 (1) : 30-35.

[8]LinderJohnF,MsaonJonathan,NeffJoseph,etal.NoninvasiveControlofStochasticResonance[J].PhysicalReviewE, 2001, 63(41): 411071-411078.

[9]陈敏,胡茑庆,秦国军. 外加信号增强随机共振在微弱信号检测中的应用[J].国防科技大学学报,2007,29 (3) :109-112.

Research on Parameters Adjustment Optimization of Bistable Stochastic Resonance System

Yang Hongna1, Hao Rujiang1, Liang Jianhua2

(1. School of Mechanical Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China; 2.Beijing Depot of Beijing Railway Bureau , Beijing 100000, China)

There are too many parameters to be adjusted when the bistable stochastic resonance system applys to the actual signal processing, and it’s difficult to determine the direction of parameters to reach a resonance state quickly. This paper discusses bistable stochastic resonance system output characteristics affected by the shape of the potential function. A kind of parameter control method based on potential function is proposed, which can reduce the parameter needed to adjust to one. Meanwhile, it can breakthrough near-adiabatic conditions in the case of a small parameter for the processing of high-frequency signals. The results of simulation and experimental data show that it’s easy and has a certain value for application.

stochastic resonance;the potential function;parameter control

2016-01-19 责任编辑:刘宪福

10.13319/j.cnki.sjztddxxbzrb.2017.01.14

河北省研究生创新资助项目(Z99910);国家自然科学基金(51375319);河北省杰出青年科学基金(E2013210113);河北省百名优秀创新人才支持计划(BR2-222)

杨红娜(1989-)，女，硕士研究生，研究方向为机电系统故障诊断。E-mail：yhn120130903@sina.com

TP277;TH17

A

2095-0373(2017)01-0076-05

杨红娜，郝如江，梁建华.双稳态随机共振系统参数调整优化研究[J].石家庄铁道大学学报:自然科学版,2017,30(1):76-80.