EEMD降噪和谱峭度法在铁路货车轴承故障诊断中的应用

李翠省, 刘永强, 廖英英

(1.石家庄铁道大学 机械工程学院，河北 石家庄 050043；2. 石家庄铁道大学 土木工程学院，河北 石家庄 050043)

EEMD降噪和谱峭度法在铁路货车轴承故障诊断中的应用

李翠省1, 刘永强1, 廖英英2

(1.石家庄铁道大学 机械工程学院，河北 石家庄 050043；2. 石家庄铁道大学 土木工程学院，河北 石家庄 050043)

针对铁路货车轴承结构复杂，早期微弱故障往往淹没于强烈的背景噪声中而难于提取的特性，提出了基于EEMD降噪和谱峭度法的共振解调技术。首先，将轮对跑合实验台上测得的振动信号进行EEMD分解；然后，根据峭度、标准相关系数选取包含故障信息较多且与原信号相关性较大的IMF分量，分别对每个IMF分量进行谱峭度分析，确定带通滤波器的最佳中心频率和带宽；最后，将滤波后的IMF分量重构并进行包络解调和频谱分析。通过对轴承内、外圈故障的实验研究,验证了该方法的有效性和可行性。该方法在铁路货车轴承早期故障诊断中具有较好的实际应用价值。

EEMD；谱峭度；货车轴承；故障诊断

0 引言

轮对轴箱轴承是铁路货车的关键部件之一，它起着连接轮对与构架的重要作用，轮对轴承状态的好坏决定着机车车辆的运行是否安全。任何早期的微弱故障隐患都会严重威胁铁路货车的安全运行，因此研究轮对轴承早期故障识别方法显得尤为重要。铁路货车轴承为双列圆锥滚子轴承，轴承结构复杂且早期微弱故障往往被噪声淹没而难于提取，因此采用传统方法进行故障诊断比较困难[1]。共振解调法又称高频共振法或包络分析法,是目前滚动轴承故障诊断中最常用的方法之一[2]，能将故障信号从高频调制信号中提取出来，但需要事先通过冲击试验来确定带通滤波器的中心频率和带宽[3]。王宏超等[4]将 kurtogram算法应用于带通滤波器参数确定中，克服了传统共振解调方法的不足。滚动轴承振动信号中的噪声严重影响共振解调故障诊断的精准性，为此必须抑制噪声，提高信噪比。小波变换方法具有多分辨性能，但降噪效果依赖于小波基的选择和阈值的确定，自适应性比较差。EMD( Empirical Mode Decomposition) 是美籍华人Norden E.Huang 等提出的一种自适应的信号消噪方法[5]，近些年发展迅速，但EMD分解存在着端点效应和频率混叠现象。Wu等针对EMD方法的不足，提出了一种噪声辅助以解决模态混叠问题的数据分析方法[6-7]—集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)方法。EEMD将信号从高频到低频逐次分解，高频部分IMF分量中含有较多的故障信息，而其中往往包含大量噪声。因此IMF分量的选取、重构成了抑制噪声突出故障信息的关键，本文将基于EEMD降噪和谱峭度法的共振解调技术应用到铁路货车轴承早期故障的诊断中。利用EEMD对信号进行分解，根据峭度和标准相关系数两个原则来优选IMF分量；采用谱峭度法确定带通滤波器的带宽和中心频率，对优选的单一IMF分量进行滤波处理。将滤波后的IMF分量重构并进行包络分析，能够精准提取到故障特征频率。

1 EEMD降噪理论

经验模态分解(EMD)是一种新的自适应信号处理方法，适用于非线性、非平稳性信号。EMD可将任意一个时间序列的信号从高频到低频逐次分解出若干个基本模式分量(Intrinsic Mode Function，IMF)和一个余项r。传统的EMD方法中因为IMF的不连续而造成模态混叠，主要原因有两个：信号中没有足够的极值点，造成分解的停止；采用三次样条函数对信号的极值点进行拟合时，由于极值点分布间隔的不均匀而造成了误差[8]。为了克服模态混叠现象，Wu等提出了EEMD方法，通过在原始信号中添加高斯白噪声并对其进行EMD分解，最后利用多次分解后的结果叠加求平均，从而避免了EMD方法可能造成的模态混叠现象。EEMD是一种噪声辅助的信号分解方法，具体步骤如下[9]

(1)在分析信号x(t)中加入正态白噪声序列

(1)

式中，k为加入的白噪声的幅值系数。

(2)利用 EMD将加入白噪声后的信号分解为一组IMF。

(3)每次加入不同的白噪声序列，重复以上步骤。

(4)利用不相关的随机序列的统计均值为零的原理，计算分解后IMF的均值，消除多次加入高斯白噪声对真实IMF的影响，最终得到EEMD分解后的IMF为

(2)

式中，N为EMD的集成次数；ci,m(t)为第m次EMD所得到的第i个IMF。

准则一：峭度

峭度是反映振动信号分布特性的数值统计量，它对冲击类故障信号的反应比较准确，十分善于对表面损伤类故障的轴承进行早期故障诊断。正常轴承的振动信号近似服从正态分布, 其峭度值约为3, 而当轴承开始出现故障时, 峭度值明显增大。由此可知, 当某些IMF的峭度值大于3时, 说明其中保留较多的故障冲击成分，峭度值越大说明保留故障信息越多。

(3)

式中，μ和σ分别是振动信号x(t)的均值和标准差；E表示取数学期望。

准则二：标准相关系数

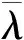
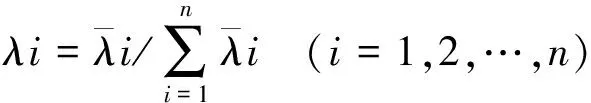
(4)

2 谱峭度理论

Antoni对谱峭度进行了深入的研究,给出了谱峭度的数学定义，并将其成功应用到旋转机械的故障诊断中[11-12]。考虑非平稳信号的Wold-Cramer分解, 定义Y(t)为由信号x(t)激励的系统响应, 则Y(t)可以表示为

(5)

式中,H(t,f)是系统的时变传递函数,可以解释为Y(t)在频率f处的复包络。

Y(t)是4阶谱累积量的谱峭度定义为

(6)

这里S2nY(f)为2n阶瞬时矩,是复包络能量的度量,定义为

(7)

将谱峭度定义为归一化累计量表示为

(8)

滚动轴承的振动信号可用如下模型表示

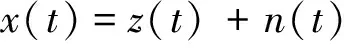
(9)

式中，x(t)为实测振动信号；z(t)为实际振动信号；n(t)为噪声信号。分别用Kx(f)和Kz(f)表示实测振动信号和实际振动信号谱峭度，则有

(10)

式中，ξ(f)为噪声与实际振动信号的功率谱密度之比。从式(10)可以明显看出，ξ(f)无穷小时即在信噪比很大的频率处，Kx(f)和Kz(f)近似相等，ξ(f)无穷大时即噪声很强的频率处，Kx(f)近似等于零。谱峭度法能够细查整个频域,通过计算整个频带的谱峭度值，找到峭度最大的频带，从而确定带通滤波器的最佳中心频率和带宽。

3 实验研究

为了验证该方法的有效性和可行性，将其应用于实测故障滚动轴承的信号中。实验中分别测量了内、外圈故障轴承和正常状态轴承。在铁路货车轮对滚动轴承故障诊断实验台上一侧安装故障轴承，另外一侧安装正常状态轴承，实验台及传感器安装位置如图1、图2所示。实验装置包括CA-YD-188型压电式加速度传感器、INV36DF型信号采集仪、信号放大器、DASP数据处理软件等。实验台采用的是RD2型轮对和与之相匹配的197726 型双列圆锥型滚动轴承。197726轴承是铁路货运列车应用最广泛的轴承之一，其主要参数和实验时的主要工况如表1、表2所示。对在实验台上测得的振动信号进行数据处理，具体流程如图3所示。

图1 轮对跑合试验台

图2 传感器安装位置

表1 197726 型轴承主要参数

表2 实验工况

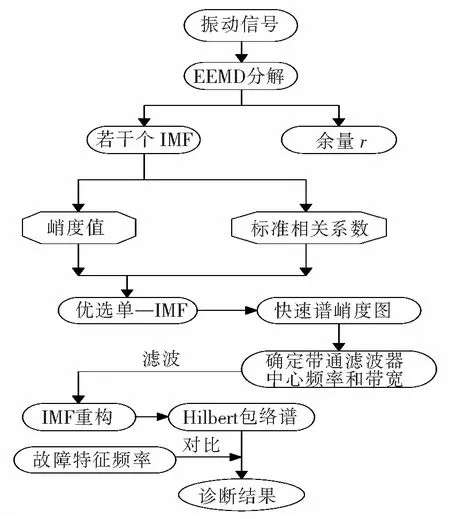
图3 轴承故障特征提取流程图

内、外圈故障信号的时域波形分别如图4、图5所示，因噪声污染,识别不出故障冲击成分。图6、图7分别为内、外圈频谱图，从图6上看不到内圈故障频率、转频和边频带，从图7上勉强可以找到外圈故障频率，但并不明显。对内、外圈故障信号进行EEMD分解，均得到16个IMF，前8个IMF的时域波形如图8、图9所示。计算各IMF的峭度、标准相关系数，如表3、表4所示。据表3知IMF1、IMF3中保留故障特征信息最多且与原信号的相关性较大，从而确定IMF1和IMF3为内圈优选分量。分别对 IMF1和IMF3进行谱峭度分析，确定带通滤波器的相关参数后进行带通滤波。把滤波后的IMF1和IMF3进行重构，如图10所示。同理，依据表4知外圈中优选分量为IMF1和IMF3，对其进行滤波，重构信号如图11所示。图10、图11较图4和图5可以看到明显的冲击成分，可知降噪效果明显。对重构的信号进行Hilbert变换及频谱分析，得到的内、外圈包络谱图，如图12、图13所示。从图12中可以看到故障特征频率为87.6 Hz(理论值87.08 Hz)及其倍频，谱线也较为明显；包络谱中可以明显看到转频7.71 Hz(理论值7.67 Hz)及其2倍频15.46 Hz；以及围绕内圈通过频率及其谐波，间距为转频的调制边带；据此特点可以判定为内圈故障。由图13中可以看出，外圈的故障特征频率为67.58 Hz，与理论值67.69 Hz高度吻合，倍频信息也很明显。

表3 轴承内圈各IMF 2个准则计算结果

表4 轴承外圈各IMF 2个准则计算结果

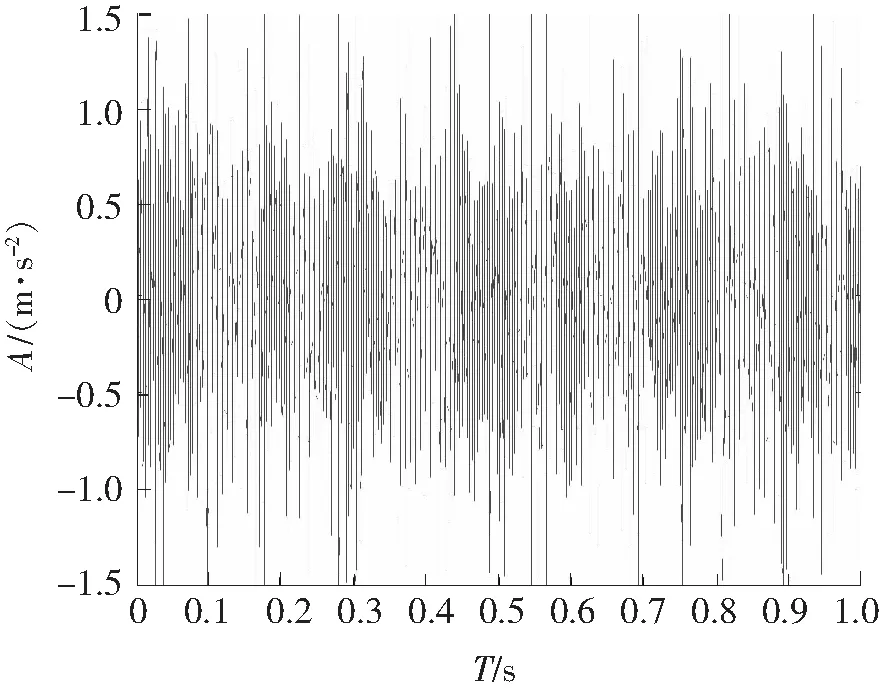
图4 内圈时域波形

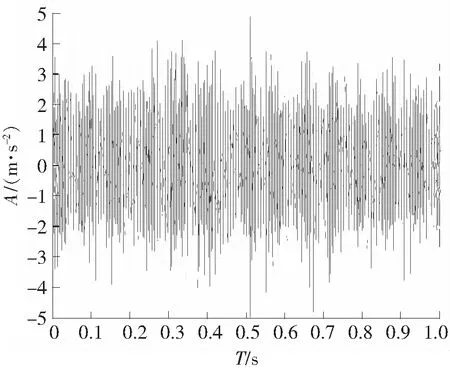
图5 外圈时域波形

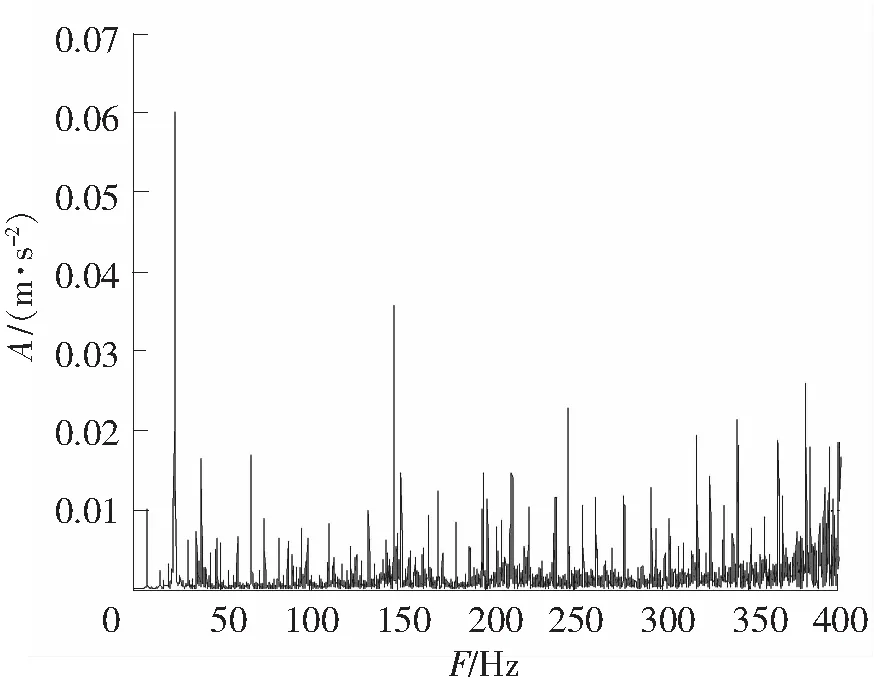
图6 内圈频谱图

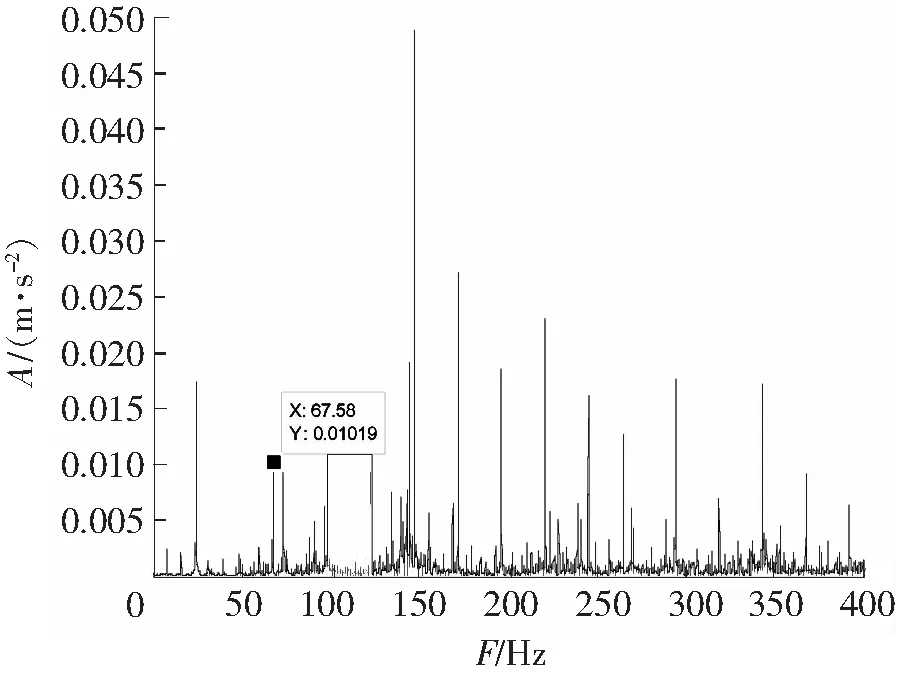
图7 外圈频谱图

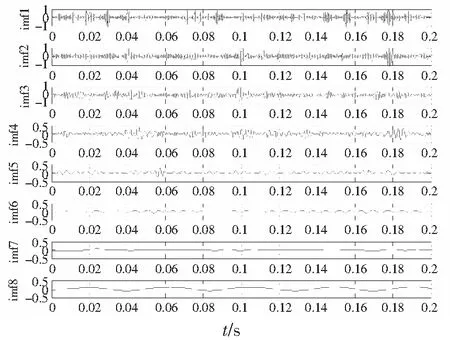
图8 内圈EEMD分解IMF时域波形

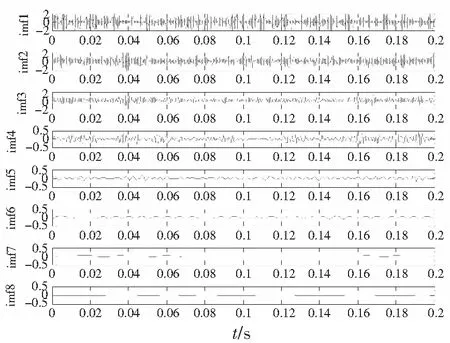
图9 外圈EEMD分解IMF时域波形

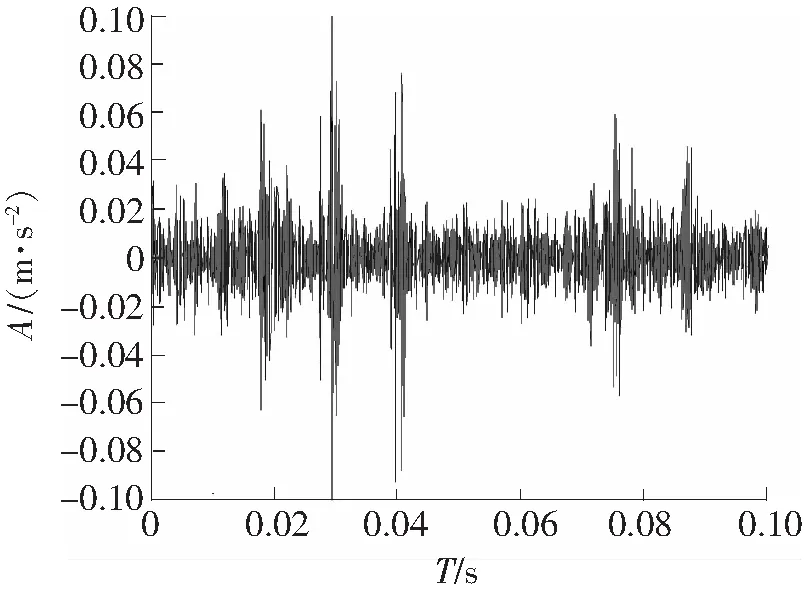
图10 内圈故障重构信号的时域波形

图11 外圈故障重构信号的时域波形

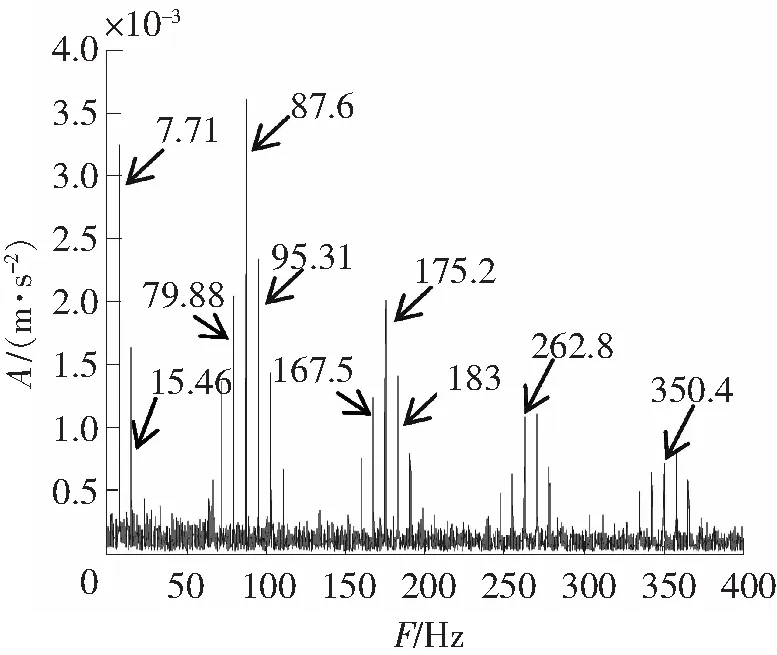
图12 内圈故障重构信号的包络谱图

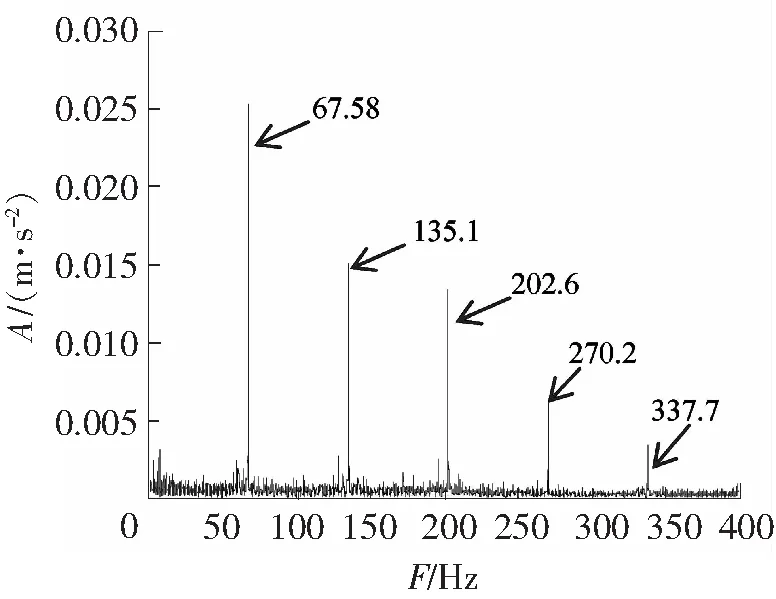
图13 外圈故障重构信号的包络谱图

4 结论

铁路货车运行环境复杂，轴承故障成分常常淹没于噪声中而难以提取。故此，将基于EEMD降噪和谱峭度法的共振解调技术应用到铁路货车轴承早期故障的诊断中。通过对铁路货车轴承内外圈故障分析，该方法可以准确地提取到故障特征信息，有效地抑制噪声。该方法可用于轴承故障精准诊断，对于铁路货车轴承的早期故障诊断具有较好的实际应用价值。

[1]侯丽娴,杨绍普,刘永强,等.基于共振解调的铁路货车轴承故障诊断[J].石家庄铁道大学学报:自然科学版,2013，26(4):47-51.

[2]丁康,陈健林,苏向荣.平稳和非平稳振动信号的若干处理方法及发展[J].振动工程学报,2003,16(1): 1-10.

[3]王平,廖明夫.滚动轴承故障诊断的自适应共振解调技术[J].航空动力学报,2005,20(4): 606-6012.

[4]王宏超,陈进,董广明,等.基于快速kurtogram算法的共振解调方法在滚动轴承故障特征提取中的应用[J].振动与冲击，2013，32(1): 35-37.

[5]Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis [J].Proceedings of the Royal Society，1998,454: 903-995.

[6]Wu Z,Huang N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method [J]. Advances in Adaptive Data Analysis, 2009,1: 1-41.

[7]Huang NE, Wu Z. A review on Hilbert-Huang transform: method and its applications to geophysical studies [J].Rev．Geophys， 2008, 46,RG2006,doi: 10, 1029 /2007RG000228.

[8]郑直,姜万录,胡浩松,等.基于EEMD形态谱和KFCM聚类集成的滚动轴承故障诊断方法研究[J].振动工程学报,2015,28(2): 324-330.

[9]张超,陈建军. EEMD方法和EMD方法抗模态混叠对比研究[J].振动与冲击,2010 (29): 237-255.

[10]Lei Y,Zuo M J,Hoseini M.The use of ensemble empirical mode decomposition to improve bispectral analysis for faultdetection in rotating machinery [J].Proceedings of the Institution of Mechanical Engineers,Part C:Journal of Mechanical Engineering Science.2009,224(8): 1759-1769.

[11]Antoni J,Randall R B. The spectral kurtosis: a useful tool for characterizing non-stationary signal [J]. Mechanical Systems and Signal Processing, 2006,20(2): 282-307.

[12]Antoni J,Randall R B.The spectral kurtosis: application to the vibratory surveillance and diagnostics of rotating machines [J]. Mechanical Systems and Signal Processing,2006,20(2): 308-331.

Application of EEMD Denoising and Spectral Kurtosis in Fault Diagnosis of Railway Wagon Bearing

Li Cuixing1, Liu Yongqiang1, Liao Yingying2

(1.School of Mechanical Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China; 2.School of Civil Engineering, Shijiazhuang Tiedao University,Shijiazhuang 050043 ,China)

Considering railway wagon bearing structure complex and early weak fault is difficult to extract in strong background noise, a resonance demodulation method based on ensemble empirical mode decomposition(EEMD)and spectral kurtosis is proposed. First, the bearing fault signal is decomposed by EEMD method. Then according to kurtosis and standard correlation coefficient, the IMF component is selected , which contains more fault information and better relevance. Each selected IMF component is analyzed with spectral kurtosis, based on this, a band-pass filter is designed to conduct filtering processing to each selected IMF component. Finally, the frequency of the impact composition is extracted by Hilbert transformation and spectrum analysis is made of the filtered composite signal. Through the experimental study on the bearing inner and outer ring fault, the method can eliminate the background noise’s interference, and can effectively diagnose the incipient fault of bearing. This method has good practical application values for early fault diagnosis of railway wagon bearing．

EEMD;spectral kurtosis;wagon bearing;fault diagnosis

2016-01-09 责任编辑:刘宪福

10.13319/j.cnki.sjztddxxbzrb.2017.01.13

国家自然科学基金(11227201，11472179，U1534204，11572206，11302137，11172182，11372199，11372197)；河北省自然科学基金(A2015210005,A2016210099)；河北省教育厅项目(YQ2014028)

李翠省(1988-),男，硕士研究生，研究方向为机车车辆故障诊断。E-mail: 854116499@qq.com

TH133.33

A

2095-0373(2017)01-0070-06

李翠省,刘永强,廖英英.EEMD降噪和谱峭度法在铁路货车轴承故障诊断中的应用[J].石家庄铁道大学学报:自然科学版,2016,30(1):70-75.