基于桥梁动力响应差和提升小波变换识别梁桥损伤

田 琦

(天津大学 建筑工程学院，天津 300072)

基于桥梁动力响应差和提升小波变换识别梁桥损伤

田 琦

(天津大学 建筑工程学院，天津 300072)

基于损伤桥梁在移动车辆荷载下的动态响应特点以及提升小波变换在奇异性检测方面的优越性能，提出了对不同大小移动车辆荷载作用下的单点桥梁加速度响应差值进行提升小波变换，通过提升小波系数峰值识别桥梁损伤的不依赖无损模型的损伤检测方法。数值分析表明,该方法可以有效识别不同程度、不同位置和多处桥梁损伤。其次，讨论了不同测点位置、荷载速度、噪声水平对损伤识别效果的影响，表明该方法具有较好的抗噪性；测点距离损伤位置越近，损伤识别效果越好；当荷载速度过大时，损伤信息易被淹没，损伤效果变差。

移动车辆荷载；提升小波变换；加速度响应差；梁桥损伤识别

0 引言

利用移动车辆荷载激励进行桥梁损伤检测的方法近年受到越来越广泛的关注，因为具有无需阻断交通、无需布置大量传感器、无需测定激励力、方便快捷、经济适用的优点，测量移动车辆荷载作用下的车桥动力响应，运用一种有效的信号分析技术进行时域信号处理和损伤检测是实现桥梁快速损伤检测的有效途径之一。

任宜春[1]应用墨西哥小波对裂纹梁在移动荷载作用下的跨中位移响应进行小波变换识别损伤。Zhu[2]将梁的裂纹损伤采用扭转弹簧单元模拟，推导了损伤梁在移动荷载下的动力响应，并对位移时程进行小波变换识别损伤。韩西[3]利用结构在完好状态和损伤状态的加速度差进行小波分析来识别结构损伤，并通过试验验证了该方法具有良好的识别效果。赵俊[4]利用梁上某一点挠度、速度、加速度信号，利用小波分析识别多位置裂纹，并研究了在多个同向和相向移动荷载作用下损伤梁的裂纹识别方法。余竹[5]利用位移互等定理和影响线的概念研究了对移动荷载下桥梁位移响应进行连续小波变换进行损伤识别的可能性，通过对移动荷载作用下桥梁的位移响应进行小波变换识别损伤，利用小波灰度图和小波系数模极大值轨迹图识别损伤位置，并通过Lipschitz指数评价损伤程度，对相关影响因素进行了参数化分析。耿佳[6]运用荷载作用下裂纹梁速度响应和连续小波变换识别结构损伤，并将小波系数局部极大值作为损伤指标评估损伤程度。Hester et al[7]建立了两轴四自由度半车模型，并且采用小波能量指标进行损伤识别，发现当路面不平顺为A级，车速为3 m/s，噪声水平为3%时，该法能够准确判定损伤位置，但随着车速的提高，该方法的有效性不断降低。张耀[8]利用损伤前后加速度响应差提升小波变换进行损伤识别。上述研究中基于损伤前后动力响应差值进行小波变换识别损伤的方法不可避免地涉及到桥梁完好状态模型，限制了其实用性。

图1 移动常量力作用下的简支梁

本文首次提出了利用不同大小移动荷载作用下的加速度响应差值，进行提升小波变换，通过提升小波系数局部极大值来表征桥梁结构损伤的方法。该方法应用于实际桥梁时，数据分析所需的所有测试数据可以在非常短的一段时间内完成采集，对于削弱温度、湿度、光照、风力等环境因素和测试误差的影响非常有利。另外，加速度是位移的二阶导数，对于损伤造成的动力响应信号奇异性会更加敏感，并且加速度在工程应用中比较容易获取，因此采用桥梁上测点的加速度响应作为信号分析的对象。首先获取移动荷载作用下桥梁加速度响应差值，并利用MATLAB小波工具箱实现提升小波变换，得到小波系数图，通过小波系数峰值识别结构损伤，并且结合算例探讨了不同影响因素下此法的有效性。

1 移动力作用下的桥梁动力响应分析

选用简支欧拉梁进行动力响应数值分析，建立的动力系统如图1所示。

振动方程如下

(1)

式中，EI为抗弯刚度；c为阻尼系数；m为单位线质量；v为荷载移动速度；δ(x-vt)为狄利克雷函数。采用了振型分解法求解，则

(2)

(3)

通过Newmark-β法求得qn(t)，代入到式(2)中即可求得简支梁的动力响应。

2 提升小波变换

提升小波变换是在传统小波分析理论的基础上的进一步演化，它由贝尔实验室的Sweldens博士于1995年提出，为了和传统小波分析方法相区别，称作第二代小波[9]，又名提升小波变换(Lifting Wavelet Transform)。相对传统方法而言，提升小波变换是一种更为高效的小波变换实现途径，它不依赖于傅立叶(Fourier)变换，完全在时域内完成双正交小波滤波器的构造，在结构化设计和自适应能力方面具有传统方法所不具备的优势。一般来说，提升小波变换和第一代小波的异同和联系可以概括如下：

(1)在构造方法上，二代小波变换运用提升方法，而传统小波则是以滤波器组频域特性为出发点，构造性质彼此不同的小波函数。

(2)在多尺度分析上，提升小波变换的小波空间和尺度空间不再由基函数伸缩平移获得，所以其多分辨空间不再具有伸缩平移不变性。

(3)传统小波变换的小波函数和尺度函数的性能在基函数构造完成后不再发生改变，而提升小波变换则可以通过提升方法持续不断地改善小波的特性。

(4)在小波种类上，传统小波变换可用的小波种类非常有限，但提升小波变换从理论上来说，则可以根据需求任意组合构造小波。

(5)传统的小波分析以频域为基础进行，而提升小波则是基于时域，但仍旧可以获得和前者相同的时频特性。

鉴于提升小波变换相比传统方法的独到之处，将它运用到桥梁结构损伤识别的问题上来，发挥它的时-频局部化特性以及对信号的自适应性，实现对非稳态信号的多尺度分析，不仅运算效率大大提升，而且存储空间需求也显著减小。传统小波采用的Mallet算法是通过低频和高频滤波器和待处理的信号进行卷积计算区分信号的低频和高频子带。而提升算法则是提出了多项式提升框架的方法构造小波，其基本思想是，将采用的小波滤波器分解为基本构造模块，分步完成小波变换的全过程，这一过程包括剖分、预测以及更新3个阶段[10]。

设初始加速度响应差S={S(k),k∈Z}，则对其进行提升小波变换识别损伤的流程如图2所示。

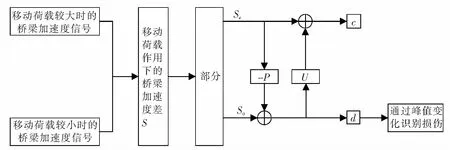
图2 基于提升小波变换的损伤识别流程

(1)分解。第一步将S={S(k),k∈Z}分解为偶样本序列Se及奇样本序列So

(4)

(5)

(2)预测。设P(·)为预测器，用偶样本序列Se(k)预测奇样本序列So(k)。用奇信号的实际值减去预测值可以得到预测误差d={d(k),k∈Z}，定义为小波的细节信号

(6)

(3)更新。设U(·)为更新器，在细节信号d(k)的基础上进行更新，并加上偶样本序列Se(k)，得到小波的近似信号c(k)

(7)

最后，通过细节信号d(k)提升小波系数图中的峰值变化识别桥梁损伤。

3 数值研究

本节通过有限元分析软件ANSYS建立损伤梁模型如图3所示，假设损伤位置距左端支座的距离为Ld，设置传感器距左端支座的距离为Lt，损伤的高度为h，采用归一化参数ld=Ld/L，lt=Lt/L分别代表损伤的相对位置、测点的相对位置，采用裂缝的相对深度δ=h/H表示损伤程度，裂缝通过损伤区域内单元刚度折减来实现，1#代表传感器，v代表移动荷载的速度。简支梁模型采用BEAM3单元模拟，跨度L=10 m，沿纵向划分为1 000个单元，弹性模量E=2.1e11 Pa，质量密度ρ=7 800 kg/m3，阻尼采用瑞雷阻尼，振形阻尼比大小取值为0.02，计算10 kN和20 kN移动荷载作用下的桥梁加速度响应差值，结合提升小波方法得到提升小波系数图，通过提升小波系数峰值变化识别梁的损伤。各损伤工况如表1所示。

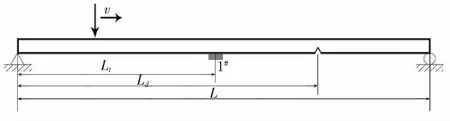
图3 移动力作用下的损伤梁模型

表1 损伤工况

下面分别考察不同损伤程度和多处损伤的识别，以及测点位置、移动荷载速度、噪声等因素对识别效果的影响。

3.1 不同损伤程度

令移动荷载的移动速度为2 m/s，移动荷载为10 kN和20 kN，不同损伤程度下的跨中加速度差时程曲线如图4所示。由图4可见，在不同的损伤程度下，移动荷载在经过损伤位置时，加速度幅值波动均十分微弱，难以从加速度谱中直接识别损伤的位置。下面对上述4个工况的跨中加速度响应差值进行提升小波变换，提升小波函数选为db7，进行尺度为6的提升小波变换，绘制细节信号的小波系数图，如图5所示。

图4 跨中加速度差

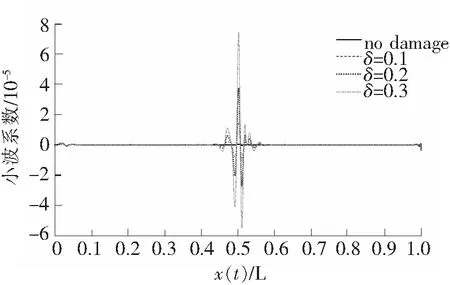
图5 不同损伤程度下的提升小波系数

由图5可见，随着损伤程度的提高，提升小波变换得到的细节信号在损伤位置处的提升小波系数峰值也相应增大，因此可以采用提升小波系数峰值来表征损伤的大小。

3.2 不同损伤位置

对工况五和工况六的跨中加速度差值进行提升小波变换，为了对比分析计算结果，仍令移动荷载速度为2 m/s。变换后得到的细节信号提升小波系数如图6、图7所示，可见，无论是单一损伤位置还是多损伤位置，使此方法都可以有效识别出来。另外，即使是无损状态下，当采用跨中测点测得的加速度信号差值作提升小波变换时，小波系数图跨中位置处会出现奇异值，但是其量级较小，不会影响损伤位置的判定。

图6 单处损伤下的提升小波系数

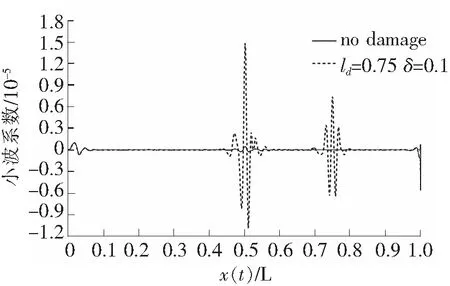
图7 两处损伤下的提升小波系数

3.3 不同测点位置

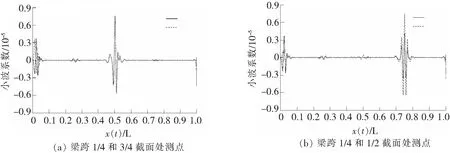
图8 不同测点位置下的提升小波系数

以损伤工况二为例，移动荷载速度为2 m/s，分别对梁跨1/4和3/4截面处测点(lt=0.25，lt=0.75)的加速度响应差进行提升小波变换，提升小波系数如图8(a)所示。以损伤工况五为例，移动荷载速度为2 m/s，分别对梁跨1/4和1/2截面处测点(lt=0.25，lt=0.5)的加速度响应差进行提升小波变换，小波系数如图8(b)所示。由图8可见：①当不同测点到损伤位置的距离相同时，除端部效应影响区域以及测点附近位置的小波系数存在差异之外，其他部分的小波系数曲线基本完全吻合。亦即采用距损伤位置同等距离的测点动力响应得到的损伤位置和程度的评价结果是一致的；②同等条件下，测点距离损伤位置越近，通过提升小波变换得到的小波系数峰值越大。

3.4 不同车速

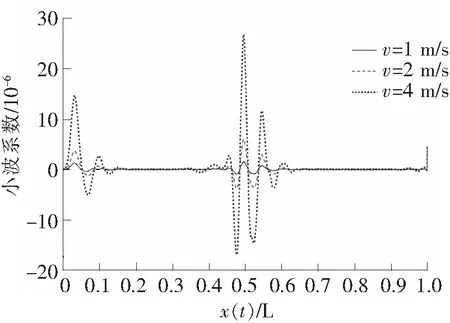
图9 不同车速下提升小波系数

以损伤工况二为例，令荷载移动速度分别为1 m/s、2 m/s、4 m/s，得到如图9所示的小波系数图。

当行车速度为1 m/s、2 m/s、4 m/s时，可以在小波系数图中识别出在损伤位置具有明显的峰值变化，随着移动荷载速度的提高，小波系数峰值也随之提高，而且并没有出现明显的峰值迁移现象，都能够准确地识别出损伤位置。而当移动荷载速度增加至8 m/s时，由于动力成分在加速度响应中的比重加大，通过提升小波变换提取的细节信号不能在损伤位置处表现出明显的峰值变化，端部效应的影响也显著增强。

3.5 噪声影响分析

在实际桥梁动载测试中，不可避免的会存在环境、设备因素和测试误差等环境噪声的影响，因此，本文所提的方法只有具备良好的抗噪性，才能实现其应用价值。下面将以损伤工况二为例，就噪声对损伤识别效果的影响进行分析。环境噪声的模拟一般采用结构响应加上一定水平的高斯白噪声来实现。高斯白噪声指的是均值为0，服从正态分布的白噪声。噪声水平通过信噪比SNR的概念来表示

(8)

式中，σS为信号的均方根，σN为环境噪声的均方根，信噪比SNR的单位为分贝(符号dB)。

由信噪比的定义可知，信噪比越小，噪声水平就越高。移动荷载速度为2 m/s，分别取值为60 dB、50 dB、45 dB、40 dB，每个噪声水平下模拟3组白噪声信号，取小波系数平均值作为损伤识别的结果。SNR=50 dB时信号附加的环境噪声如图10所示，各个噪声水平下的分析结果如图11所示。

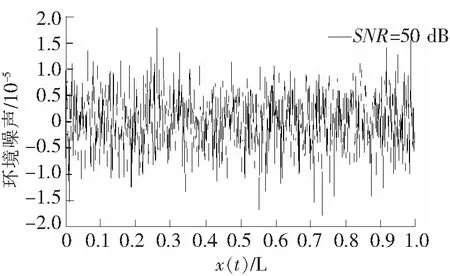
图10 环境噪声

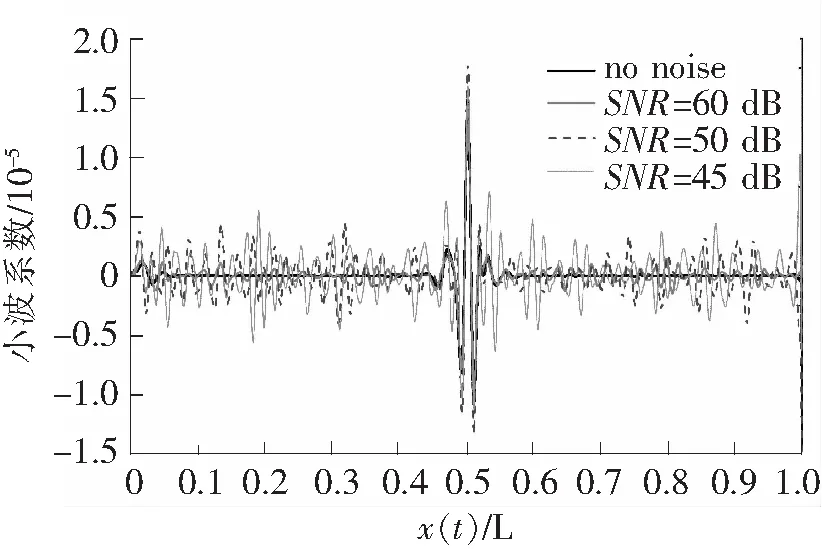
图11 不同环境噪声下的提升小波系数

可见，当信噪比为60 dB、50 dB、45 dB时，仍然可以在跨中损伤位置观测到小波系数峰值，且峰值的大小近似相等，但是随着信噪比的下降，噪音水平的提高，小波系数的空间起伏变化越来越剧烈，经研究发现，当信噪比低于40 dB时，损伤信息被环境噪声完全淹没，难以识别损伤的位置。因此，如何消除高噪声的影响还有待于进一步研究。

4 结论

(1)对于不同损伤程度、损伤位置和多损伤工况下的桥梁损伤，均可以通过桥梁单点动力响应差提升小波系数峰值有效地识别出来。

(2)传感器位置距离损伤位置越近，识别效果越好。

(4)随着荷载速度的提高，小波系数峰值随之增大，但当行车荷载速度过高时(v≥8 m/s)，损伤信息易被动力响应淹没，对损伤识别造成困难。

(5)本文的方法无需阻断交通、无需布置大量传感器、无需测定激振力，无需基准模型、方便快速、经济适用。

[1]任宜春，马石城，林琳.移动荷载作用下梁裂缝识别的小波方法研究[J].振动与冲击,2004(2):84-87.

[2]Zhu X Q, Law S S. Wavelet-based crack identification of bridge beam from operational deflection time history[J].International Journal of Solids and Structures, 2006, 43(7/8): 2299-2317.

[3]韩西，崔璟，钟厉，等. 小波分析在T梁结构损伤识别中的应用研究[J]. 地震工程与工程振动,2011(1): 101-105.

[4]赵俊，张伟伟，马宏伟. 移动载荷作用下简支梁的动态响应及裂纹损伤识别研究[J]. 振动与冲击,2011(6):97-103.

[5]余竹，夏禾. 基于移动荷载作用下的结构响应及小波分析的桥梁损伤诊断[J]. 北京交通大学学报,2014, 38(3): 55-61.

[6]耿佳，张伟伟，赵子龙，等. 移动载荷下桥梁速度响应小波分析多裂纹识别[J]. 太原科技大学学报,2014, 35(1):69-76.

[7]Hester D, Gonzalez A. A wavelet-based damage detection algorithm based on bridge acceleration response to a vehicle[J].Mechanical Systems and Signal Processing,2012, 28(S1): 145-166.

[8]张耀. 基于车致振动和提升小波的梁式桥损伤识别研究[D].郑州：郑州大学, 2014.

[9]孙增寿，范科举，张波. 基于第二代小波变换的结构损伤检测研究进展[J]. 郑州大学学报：工学版， 2010, 31(1): 1-5.

[10]何正嘉. 现代信号处理及工程应用[M].成都：西南交通大学出版社, 2007.

Identification of Bridge Damage Based on Bridge Dynamic Response Difference and Lifting Wavelet Transform

Tian Qi

(School of Civil Engineering, Tianjin University, Tianjin 300072, China)

Based on the characteristics of dynamic response of damaged bridges under moving vehicle loads and the superior performance of the lifting wavelet transform in the field of singularity detection, this paper proposes a damage detection method without dependence on lossless model, which applies lifting wavelet transform on bridge acceleration difference under different sizes of moving vehicle loads and then identifies the bridge damage through lifting wavelet coefficients. The numerical analysis shows that the method can effectively identify the different degrees, different positions and multiple bridge damages. Secondly, the effects of different measurement points, load speed and noise level on the damage identification results are discussed. The results show that the method has good noise immunity. The smaller the distance between the measuring points and the damage position, the better the damage identification effect. When the load velocity is too large(v=8 m/s), the damage information is easy to be submerged, and the damage effect becomes worse.

moving vehicle load;lifting wavelet transform;acceleration response difference;damage detection of girder bridge

2015-12-05 责任编辑:车轩玉

10.13319/j.cnki.sjztddxxbzrb.2017.01.04

田琦(1991-)，男，硕士研究生，主要从事桥梁损伤识别的研究。 E-mail: tianqi_19910810@163.com

TU312

A

2095-0373(2017)01-0019-06

田琦.基于桥梁动力响应差和提升小波变换识别梁桥损伤[J].石家庄铁道大学学报:自然科学版,2017,30(1):19-24.