非保守系统的Lagrange方程

周平, 梁立孚

(1.哈尔滨工程大学 机电工程学院，黑龙江 哈尔滨 150001；2. 哈尔滨工程大学 航天与建筑工程学院，黑龙江 哈尔滨 150001；3. 黑龙江科技大学 机械工程学院，黑龙江 哈尔滨 150022)

非保守系统的Lagrange方程

周平, 梁立孚

(1.哈尔滨工程大学 机电工程学院，黑龙江 哈尔滨 150001；2. 哈尔滨工程大学 航天与建筑工程学院，黑龙江 哈尔滨 150001；3. 黑龙江科技大学 机械工程学院，黑龙江 哈尔滨 150022)

如何将Lagrange方程应用于连续介质动力学，一直是学术界关注的理论课题。如何将Lagrange方程应用于非保守连续介质动力学的问题的研究难度更大。本文应用Lagrange-Hamilton体系，非保守系统的Lagrange方程是非保守系统的Hamilton型拟变分原理的拟驻值条件，成功地将Lagrange方程应用于非保守连续介质动力学。进而应用非保守系统的Lagrange方程推导出非保守连续介质动力学的控制方程，为研究非保守连续介质动力学开辟了一条新的有效途径。

连续介质动力学；Lagrange方程；非保守系统；拟变分原理；拟驻值条件；Lagrange-Hamilton体系

非保守系统的Lagrange方程的研究涵盖了许多学科，是一个相当重要的研究领域。对于非保守系统, Leipholz提出了广义自共轭的概念，建立了广义的Hamilton原理，给出了著名的Leipholz杆模型，在非保守系统变分原理方面进行了开创性研究[1-4]。我国学者通过发展Leipholz的研究，并发扬国内对广义变分原理研究的优势，在伴生力系统的前提下，建立了非保守系统的余能原理，进而建立了关于弹性理论非保守系统的一般变分原理[5]。文献[6]从虚功原理出发，建立了非保守系统的有限变形弹性拟变分原理；文献[7]基于非线性弹性理论三类共轭变量对应的6种基本方程，建立了12种互相有联系的非保守动力体系的拟广义变分原理；文献[8]建立了非线性弹性理论变分原理的统一理论；文献[9]给出并证明了微极弹性动力学中非保守力场问题的几种拟变分原理，其结果还可以推广到非局部弹性介质和非局部微极弹性介质力学中去。文献[10]从泛能量泛函出发，提出了非线性弹性理论静、动力学的非保守问题的统一变分原理——泛变分原理。文献[11]建立了非保守系统自激振动的拟固有频率变分原理。文献[12]研究了非保守系统的拟变分原理的静态和动态稳定性问题。但是，关于如何将Lagrange方程应用于非保守系统连续介质动力学的文献极少。

梁立孚等系统地研究了非保守系统弹性(动)力学的拟变分原理[13-15]；研究了非保守系统刚体动力学的拟变分原理[16]；研究了非保守系统分析力学的拟变分原理[17]。文献[18-19]将非保守系统的拟变分原理推广应用于航天动力学中去，实现了质点刚体力学与变形体力学的耦合，能够解决航天动力学中的一些重要问题。经过多年研究的积累，逐步形成一部专著[20]。专著[20]中已经注意到，在经典分析力学中非保守系统的Lagrange方程是保守系统的Lagrange方程加上非保守广义力项。

本文采用Lagrange-Hamilton体系，对于保守系统，Lagrange方程是Hamilton原理的驻值条件；对于非保守系统，Lagrange方程是Hamilton型拟变分原理的拟驻值条件。本文根据这一结论，分别论述了非保守刚体动力学、非保守弹性动力学和粘弹性动力学的Lagrange方程，并应用Lagrange方程推导非保守弹性动力学和粘弹性动力学的控制方程。

1 非保守系统分析动力学的Lagrange方程

非保守分析动力学两类变量的拟Hamilton原理：

δΠH2-δQH=0

(1)

其中

以下推导拟Hamilton原理的拟驻值条件。为此， 将式(1)写成展开形式：

δΠH2-δQH=

(2)

考虑到:

(3)

可得

(4)

进行分部积分：

(5)

将式(5)代入式(4)，按惯例在时域边界t=t0和t=t1处取δq=0，可得

(6)

由于δq的任意性，故由式(6)可得非保守分析动力学两类变量的拟Hamilton原理的拟驻值条件为

(7)

可见，非保守分析动力学两类变量的拟Hamilton原理的拟驻值条件即为非保守分析动力学两类变量的Lagrange方程。

非保守分析动力学一类变量的拟Hamilton原理：

δΠH1-δQH=0

(8)

其中

应用类似方法，可得非保守分析动力学一类变量的拟Hamilton原理的拟驻值条件为

(9)

可见，非保守分析动力学一类变量的拟Hamilton原理的拟驻值条件即为非保守分析动力学一类变量的Lagrange方程。

2 非保守系统刚体动力学的Lagrange方程

如果认为导致刚体运动的力为保守的广义力F和非保守广义力FN，保守的广义力矩M和非保守广义力矩MN，即作用于质心的主矢为F和FN， 而主矩为M和MN，则非保守系统刚体动力学的拟Hamilton原理表示为

δπH1-δQH=0

(10)

式中

M·θ+FN·Xc+MN·θ)dt

其中, 系统的动能为

(11)

系统的势能为

U=-F·Xc-M·θ

(12)

系统的拟势能为

Uq=-FN·Xc-MN·θ

(13)

系统的余虚功为

(14)

应用对合变换，可将刚体动力学的拟Hamilton原理变换为

δπH2-δQH=0

(15)

式中

M·θ+FN·Xc+MN·θ)dt

其中, 系统的动能为

(16)

系统的势能为

U=-F·Xc-M·θ

(17)

系统的拟势能为

Uq=-FN·Xc-MN·θ

(18)

系统的余虚功为

(19)

其先决条件为

(20)

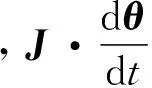
以下通过推导刚体动力学的拟Hamilton原理的拟驻值条件，得到其Lagrange方程。为此，将式(15)写成展开形式δπH2-δQH=

FN·δXc+MN·δθ)dt=0

(21)

先决条件的变分式为

(22)

将式(22)代入式(21)，可得

δπH2-δQH=

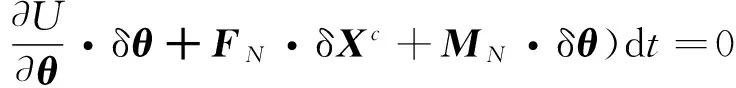
(23)

应用Green定理(分部积分)，考虑到转动惯量张量的对称性，则有

(24)

(25)

将式(24)、(25)代入式(23)，并且按惯例在时域边界t=t0和t=t1处，取δXc=0，δθ=0，可得

δπH2-δQH=

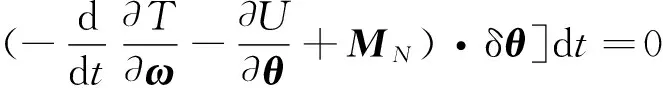
(26)

由于δXc，δθ的任意性，故由上式可得拟驻值条件为

(27)

(28)

这就是非保守系统刚体动力学两类变量的Lagrange方程。

如果将先决条件(20)代入式(27)、(28)，可得

(29)

(30)

这就是非保守系统刚体动力学一类变量的Lagrange方程。

由以上分析可见，对于质点刚体动力学，非保守系统的Lagrange方程等于保守系统的Lagrange方程加上非保守广义力。需要说明一下，这里的相加一般指的是代数相加。

3 非保守系统弹性动力学的Lagrange方程

3.1 推导非保守系统弹性动力学的Lagrange方程

非保守系统弹性动力学两类变量的拟Hamilton原理：

δΠH2-δQH=0

(31)

式中:

其先决条件为

=0, 在V内

(32)

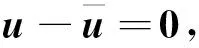
(33)

(34)

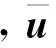
将式(32)、(34)代入式(31)，可得

δΠH1-δQH=0

(35)

式中:

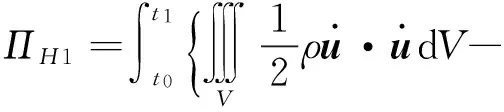
其先决条件为式(33)。这就是非保守系统弹性动力学一类变量的拟Hamilton原理。其中，系统的动能为

(36)

系统的势能为

(37)

系统的拟势能为

(38)

非保守系统的余虚功为

(39)

以下通过推导拟Hamilton原理的拟驻值条件得到Lagrange方程。为此，将式(35)写成展开形式：

δΠH1-δQH=

(40)

进行分部积分

(41)

将式(41)代入式(40)，按惯例在时域边界t=t0和t=t1处取δu=0，并且考虑到位移边界条件的变分式δu=0，可得

(42)

因为

(43)

故有

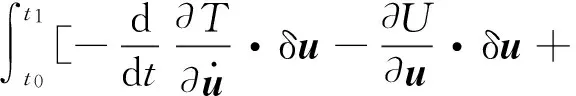
(44)

由于δu的任意性，故由式可得非保守弹性动力学一类变量的Lagrange方程：

(45)

用类似的方法可以推导出非保守系统弹性动力学两类变量的Lagrange方程，不赘述。

3.2 应用Lagrange方程推导非保守系统弹性动力学的控制方程

非保守系统线性弹性动力学的动能可以表示为

(46)

线性弹性动力学的势能可以表示为

(47)

非保守系统线性弹性动力学的拟势能和余虚功可以表示为

(48)

(49)

位移边界条件为

u-ū=0

(50)

Lagrange方程表示为

(51)

推导计算Lagrange方程中的各项：

(52)

势能变导项的推导较为复杂：

(53)

(54)

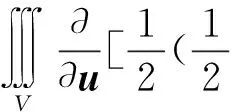
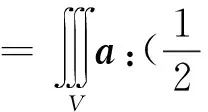
(55)

应用Green定理，并考虑到式(50)，可得

(56)

将相关各式代入Lagrange方程，可得

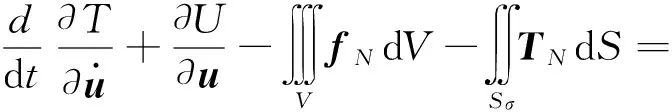
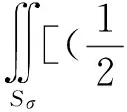
(58)

脱去积分号，可得非保守弹性动力学控制方程：

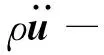
u+u):a]-f-fN=0

(59)

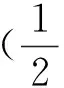
(60)

先决条件为式(50)。

应用类似方法，可得非保守弹性动力学两类变量的控制方程：

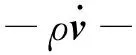
·ε:a-f-fN=0

(61)

ε:a·n-T-TN=0

(62)

由以上分析可见，对于连续介质动力学，当作用非保守体积力和面积力时，“非保守系统的Lagrange方程等于保守系统的Lagrange方程加上非保守广义力”的论述原则上是正确的，但是非保守体积力和面积力均取积分形式。

4 粘弹性动力学的Lagrange方程

粘弹性动力学的本构方程由弹性和粘性两部分组成，弹性部分服从广义胡克定律，粘性部分服从广义牛顿粘性定律。弹性部分的问题，在上一节中已得到解决；粘性部分的问题与粘性流体力学的问题相类似，由于本文作者较好的解决了Lagrange方程应用于粘性流体动力学的问题，这里应用同样的方法来解决粘弹性动力学中粘性部分的问题。应用Kelvin模型，粘弹性本构关系(μ为粘性系数)表示为

σ=a:ε+μ(v+v)(两类变量)

(63)

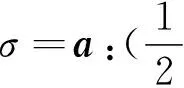
(一类变量)

(64)

需要说明一下，在工程应用中，多数文献给出粘弹性本构关系的简化形式。本文属于基础理论研究，这里给出的是粘弹性本构关系的一般表达式。

非保守系统粘弹性动力学两类变量的拟Hamilton原理：

δΠH2-δQH=0

(65)

式中

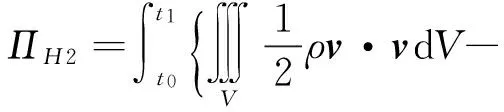
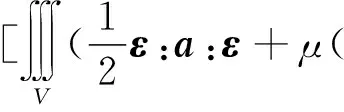
其先决条件为

=0， 在V内

(68)

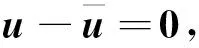
(69)

(70)

将式(68)、(70)代入式(65)，可得

δΠH1-δQH=0

(71)

式中:

(72)

(73)

其先决条件为式(69)。这就是非保守系统粘弹性动力学一类变量的拟Hamilton原理。其中，系统的动能为

(74)

系统的势能为

(75)

将粘性阻力引起的流体剪切应力视为非保守广义力，表示为τN=μ(vq+vq)，则系统的拟势能为

(76)

非保守系统的余虚功为

(77)

参照第3节的论述，通过推导拟Hamilton原理的拟驻值条件得到粘弹性动力学一类变量的Lagrange方程：

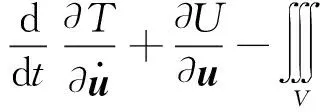
(78)

用类似的方法可以推导出非保守系统粘弹性动力学两类变量的Lagrange方程，不赘述。

同样，参照第3节的论述，可以应用粘弹性动力学的Lagrange方程推导出粘弹性动力学的控制方程：

(79)

(80)

应用类似方法，可得非保守粘弹性动力学两类变量的控制方程：

·[ε:a+μ(v+v)]-f-fN=0

(81)

[ε:a+μ(v+v)]·n-T-TN=0

(82)

由以上分析可见，对于连续介质动力学，当同时作用非保守体积力和面积力与非保守内应力时，“非保守系统的Lagrange方程等于保守系统的Lagrange方程加上非保守广义力”的论述原则上是正确的，但是非保守体积力和面积力与非保守内应力均取积分形式。

5 结束语

本文采用Lagrange-Hamilton体系，对于保守系统，Lagrange方程是Hamilton原理的驻值条件；对于非保守系统，Lagrange方程是Hamilton型拟变分原理的拟驻值条件。借助于Hamilton型拟变分原理推导出Lagrange方程，并且应用连续介质动力学的Lagrange方程推导其控制方程。论文涉及质点刚体动力学、非保守系统弹性动力学和粘弹性动力学，可以说较全面地解决了将Lagrange方程应用于非保守系统动力学的问题。

[1]LEIPHOLZ H H E. On the sufficiency of the energy criterion for the stability of certain nonconservative systems of the follower-load type[J]. Journal of applied mechanics, 1972, 39(3): 717-722.

[2]LEIPHOLZ H H E. On certain nonconservative elastic systems having divergence buckling loads[J]. Mechanics research communications, 1974, 1(4): 245-249.

[3]LEIPHOLZ H H E. Direct variational methods and eigenvalue problems in engineering[M]. Leyden: Noordhoff International Publishing, 1977.

[4]LEIPHOLZ H H E. On some developments in direct methods of the calculus of variations[J]. Applied mechanics reviews, 1987, 40(10): 1379-1392.

[5]刘殿魁, 张其浩. 弹性理论中非保守问题的一般变分原理[J]. 力学学报, 1981, 17(6): 562-570. LIU Diankui, ZHANG Qihao. Some general variational principles for non-conservative problems in theory of elasticity[J]. Chinese journal of theoretical and applied mechanics, 1981, 17(6): 562-570.

[6]熊跃熙. 非保守系统的有限变形弹性变分原理[J]. 力学学报, 1983, 19(1): 86-90. XIONG Yaoxi. Variational principles of finite deformation of elasticity in nonconservative systems[J]. Chinese journal of theoretical and applied mechanics, 1983, 19(1): 86-90.

[7]金伏生. 关于非保守非线性动力弹性理论的广义变分原理[J]. 固体力学学报, 1985(1): 57-62. JIN Fusheng. The generalized variational principle for non-conservative non-linear elastokinetics[J]. Acta mechanica solida sinica, 1985(1): 57-62.

[8]郭仲衡. 非线性弹性理论变分原理的统一理论[J]. 应用数学和力学, 1980, 1(1): 5-23. GUO Zhongheng. Unified theory of variational principles in non-linear theory of elasticity[J]. Applied mathematics and mechanics, 1980, 1(1): 5-23.

[9]戴天民, 扶名福, 林钟祥, 等. 微极弹性动力学中非保守力场问题的变分方法[J]. 应用数学和力学, 1987, 8(11): 943-952. DAI Tianmin, FU Mingfu, LIN Zhongxiang, et al. Variational Methods for the problems of nonconservative force fields in the micropolar elastodynamics[J]. Applied mathematics and mechanics, 1987, 8(11): 943-952.

[10]郑泉水. 非线性弹性理论的泛变分原理[J]. 应用数学和力学, 1984, 5(2): 205-216. ZHENG Quanshui. Extended variational principle in non-linear theory of elasticity[J]. Applied mathematics and mechanics, 1984, 5(2): 205-216.

[11]黄玉盈, 王武久. 弹性非保守系统的拟固有频率变分原理及其应用[J]. 固体力学学报, 1987(2): 127-136. HUANG Yuying, WANG Wujiu. Variational principles for the quasi-natural frequency of nonconservative elastic systems and their applications[J]. Acta mechanica solida sinica, 1987(2): 127-136.

[12]宋志远, 万虹, 梅占馨. 非保守力作用下矩形薄板的稳定问题[J]. 固体力学学报, 1991, 12(4): 359-363. SONG Zhiyuan, WAN Hong, MEI Zhanxin. Stability of plates subjected to nonconservative forces[J]. Acta mechanica solida sinica, 1991, 12(4): 359-363.

[13]LIANG Lifu, LIU Diankui, SONG Haiyan. The generalized quasi-variational principles of non-conservative systems with two kinds of variables[J]. Science in China series G: physics and astronomy, 2005, 48(5): 600-613.

[14]梁立孚, 罗恩, 刘殿魁. 非保守弹性动力学初值问题的简单Gurtin型拟变分原理[J]. 固体力学学报, 2007, 28(3): 224-228. LIANG Lifu, LUO En, LIU Diankui. Simple Gurtin type quasi-variational principles about initial value problem of non-conservative elasto-dynamics[J]. Acta mechanica solida sinica, 2007, 28(3): 224-228.

[15]梁立孚, 刘宗民, 刘殿魁. 非保守薄壁结构系统的广义拟余Hamilton原理及其应用[J]. 工程力学, 2008, 25(10): 60-65. LIANG Lifu, LIU Zongmin, LIU Diankui. Generalized Hamilton-type quasi-complementary energy principle of non-conservative thin-wall structural system and its application[J]. Engineering mechanics, 2008, 25(10): 60-65.

[16]梁立孚, 郭庆勇. 刚体动力学的拟变分原理及其应用[J]. 力学学报, 2010, 42(2): 300-305. LIANG Lifu, GUO Qingyong. The quasi-variational principles of rigid-body dynamics and their applications[J]. Chinese journal of theoretical and applied mechanics, 2010, 42(2): 300-305.

[17]周平, 赵淑红, 梁立孚. 含阻尼非保守分析力学的拟变分原理[J]. 北京理工大学学报, 2009, 29(7): 565-569. ZHOU Ping, ZHAO Shuhong, LIANG Lifu. Quasi-variational principles on non-conservative analytical mechanics with damping[J]. Transactions of Beijing institute of technology, 2009, 29(7): 565-569.

[18]LIANG Lifu, SONG Haiyan. Non-linear and non-conservative quasi-variational principle of flexible body dynamics and application in spacecraft dynamics[J]. Science China physics, mechanics and astronomy, 2013, 56(11): 2192-2199.

[19]赵淑红, 梁立孚, 周平. 带有可伸展平动附件多柔体簇系统动力学拟变分原理及其应用[J]. 工程力学, 2011, 28(6): 29-39. ZHAO Shuhong, LIANG Lifu, ZHOU Ping. Quasi-variational principles of flexible multi-body cluster system dynamics with annex of extendable translation and their applications[J]. Engineering mechanics, 2011, 28(6): 29-39.

[20]梁立孚, 宋海燕, 樊涛, 等. 非保守系统的拟变分原理及其应用[M]. 北京: 科学出版社, 2015. LIANG Lifu, SONG Haiyan, FAN Tao, et al. Quasi-variational principles of non-conservative system and their applications[M]. Beijing: Science Press, 2015.

Lagrange equation of non-conservative systems

ZHOU Ping1，3, LIANG Lifu2

(1. College of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin 150001, China; 2. College of Aerospace and Civil Engineering Harbin Engineering University, Harbin 150001, China; 3. College of Mechanical Engineering, Heilongjiang University of Science and Technology, Harbin 150022, China)

How to apply the Lagrange equation to continuum dynamics has always been a theoretical subject in the academic field. How to apply the Lagrange equation to the problem of non-conservative continuum dynamics is even more difficult. The Lagrange equation of non-conservative systems is a quasi-stationary condition for the Hamiltonian quasi-variational principle of non-conservative systems using the Lagrange-Hamilton system. In this paper, the Lagrange equation was successfully applied to non-conservative continuum dynamics. Then, the governing equations of non-conservative continuum dynamics were deduced by the Lagrange equation of non-conservative systems, which opens up a new effective way of studying non-conservative continuum dynamics.

continuum dynamics; Lagrange equation; non-conservative system; quasi-variational principle; quasi-stationary condition; Lagrange-Hamilton system

2016-06-07.

日期：2017-01-11.

国家自然科学基金项目(10272034).

周平(1978-), 女, 副教授； 梁立孚(1939-), 男, 教授,博士生导师.

梁立孚，E-mail: lianglifu@hrbeu.edu.cn.

10.11990/jheu.201606026

O313

A

1006-7043(2017)03-0452-08

周平, 梁立孚.非保守系统的Lagrange方程 [J]. 哈尔滨工程大学学报, 2017, 38(3):452-459.

ZHOU Ping, LIANG Lifu. Lagrange equation of non-conservative systems[J]. Journal of Harbin Engineering University, 2017, 38(3):452-459.

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20170111.1509.040.html