基于LUR/BME的海岸带地区PM2.5时空特性研究

江曲图,何俊昱,王占山,叶观琼*,陈 倩,肖 璐

(1.浙江大学海岛海岸研究所,浙江 舟山 316021；2.北京市环境保护监测中心,北京 100048；3.江西师范大学地理与环境学院,江西 南昌 330022)

基于LUR/BME的海岸带地区PM2.5时空特性研究

江曲图1,何俊昱1,王占山2,叶观琼1*,陈 倩3,肖 璐1

(1.浙江大学海岛海岸研究所,浙江 舟山 316021；2.北京市环境保护监测中心,北京 100048；3.江西师范大学地理与环境学院,江西 南昌 330022)

以高程、距海距离、道路、归一化植被指数构建大区域土地利用回归模型LUR,并结合贝叶斯最大熵BME对LUR模型的残差进行时空分析,得到2015年中国沿海部分省市PM2.5的时空分布.交叉验证结果表明在引入BME模型后R2由0.36提高至0.85,均方根误差RMSE由23.53µg/m3降低至 11.08µg/m3;整体海岸带地区以长江三角洲为界PM2.5浓度呈现南低北高,且以京津冀及山东内陆区域秋冬季污染最为严重,同时以山东省为例进行各市室外人口空气污染暴露分析,表明沿内陆至近海,人均PM2.5暴露浓度逐步递减,以济南85.5µg/m3最高,沿海区域烟台,威海等地较低.

土地利用回归；贝叶斯最大熵；PM2.5；人体暴露

随着我国城市化进程的加快,各地区工业发展迅速,工业排放及汽车保有量逐年增加,导致我国部分地区PM2.5空气污染严重,灰霾天气明显增加[1-2].而我国自2012年底才开展PM2.5全面监测,其覆盖点位稀疏且设备昂贵,如何获得高时空分辨率的PM2.5分布对于环境管理,空间流行病研究等意义重大[3-4].

土地利用回归模型(LUR)利用观测站点周围的多种自然环境因子进行线性回归建模,得到未观测区域的空气污染物浓度,其作为一种简单易操作的数学模型在污染物浓度空间制图方面广为使用[2,5-8].国外利用LUR模型对空气污染进行空间制图已在多伦多(NO2)[9],加利福利亚(PM2.5)[10],德黑兰(SO2)[11]等众多城市得到实践.国内[12]首次在2009年采用了不同缓冲区道路长度,土地利用,人口密度等构建LUR模型对天津市PM2.5及NO2进行了空间分布制图.随后相关学者分别在济南(SO2,NO2,PM10)[13],北京(PM2.5)[6],长沙(NO2,PM10)[14],上海(NO2,PM2.5)[15]等城市构建LUR模型对空气污染空间分布制图.但LUR模型存在空间迁移能力较差,适用于小尺度研究区域及无法充分考虑时间变异等缺陷[16-19].

现代时空地统计学贝叶斯最大熵(BME)作为一种严谨科学的时空数据分析方法则能很好的综合各种数据来源达到更精细化的时空制图.传统空间插值方法包括泰森多边形法,反距离权重法(IDW),克里金(kriging)等.而其中应用最广效果最好的则是克里金插值方法,然而克里金一般限于对实测数据空间尺度上的插值,忽略了其时间序列上的相关性,且假设数据无不确定性,正态分布等,这些都限制了数据利用的多样性及制图的精确性.BME则能考虑到数据的不确定性及时间上的关联,与传统地统计学相比其是非线性插值,不要求人为的正态分布且能与各种来源数据及方法相结合,通过对台北地区PM2.5分布制图LUR模型中引入BME,平均误差从2.78降低至2.15[17];此外,通过在整个美国PM2.5时空特性研究中对LUR辅助变量是否加入遥感数据及其与BME结合方法的比较,结果表明在引入BME后,均方根误差(RMSE)由15.91降低至4.63[20].

我国目前利用LUR模型对PM2.5分布制图研究仍限于中小城市,且较少考虑时间变异,对于预测大范围区域的PM2.5质量浓度分布精度不高.本文以我国部分海岸带地区为研究区域,采用贝叶斯最大熵BME时空数据分析方法,通过易获取的数据源,结合LUR模型残差进行时空分析,对中国沿海部分省市PM2.5时空分布进行研究,得到高精度的格点分布数据,并以山东省为例,对各市室外PM2.5人体暴露进行分析对比,进一步验证该方法的应用价值.

1 数据与方法

1.1 研究区域及数据

本研究选取我国部分沿海省市,包括北京、天津、河北、山东、江苏、上海、浙江、福建、广东由北至南沿海的3个直辖市和6个省份(图1),纵跨渤海,黄海,东海及南海,包括珠江三角洲,长江三角洲及京津冀,这几个区域是我国人口密度极高,工商业最为发达的地区,其环境健康问题备受关注,研究该区域海岸带城市PM2.5时空变化对于指导环境治理及开展我国环境健康与人体暴露等研究意义重大.

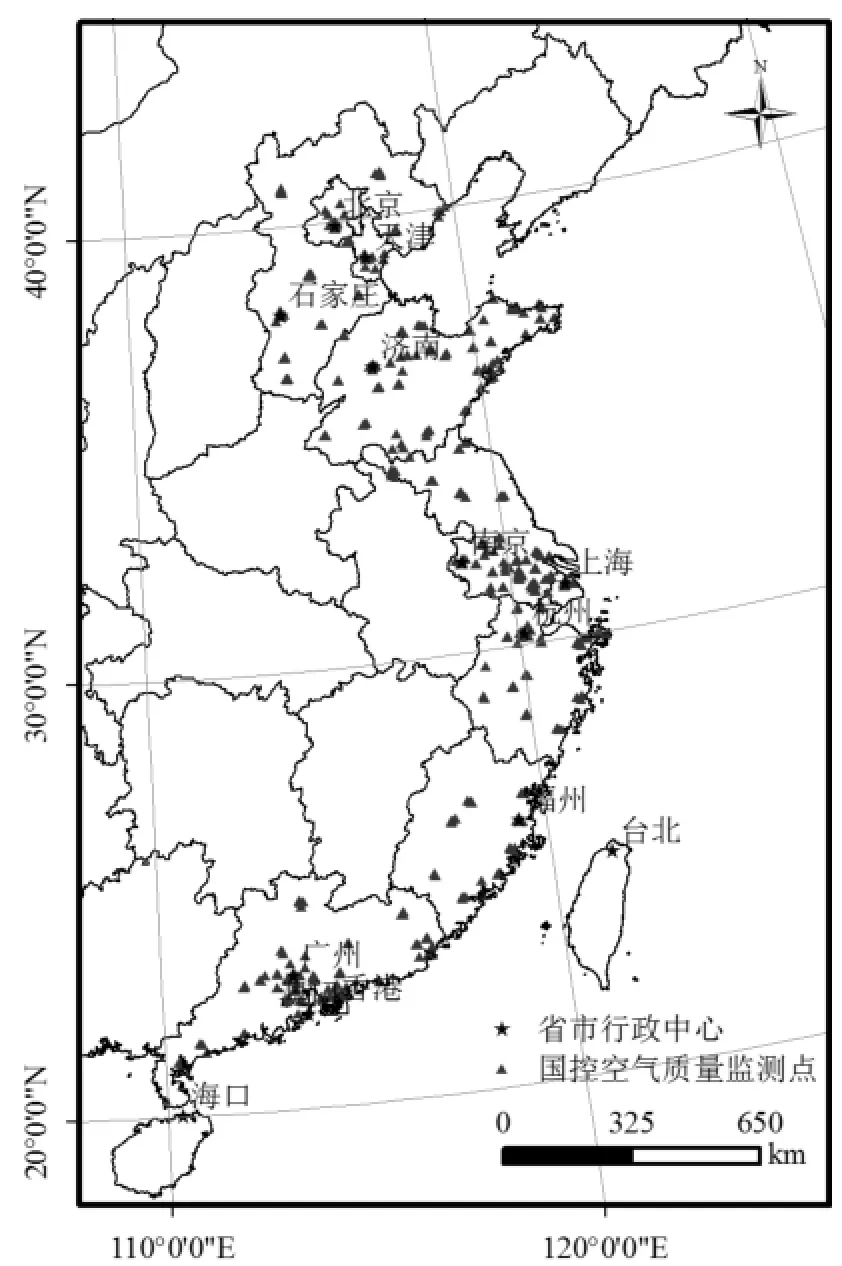
图1 研究区域内PM2.5监测站点空间分布Fig.1 Spatial distribution of PM2.5monitoring sites in this study

研究数据包括:(1)2015年PM2.5月平均数据,来源于中国环境监测总站网上发布平台(http://www.cnemc.cn),共448个国家站点PM2.5质量浓度小时观测值(部分站点数据缺失已移除),以日平均值算得448个站点5376个月平均PM2.5质量浓度观测值,由箱线图(图2)可知各站点观测数值展现了较大的空间变异及时间变异特性;(2)DEM高程数据,来源于SRTM全球90m分辨率高程数据(http://srtm.csi.cgiar.org);(3)归一化植被指数NDVI数据,从中国科学院计算机网络信息中心国际科学数据镜像网站(http://www.gscloud.cn)上下载全国2015年各月NDVI;(4)研究区域道路矢量图来源于Wiki世界地图数据库(http://www.openstreetmap.org);(5)人口密度数据来源于哥伦比亚大学社会经济数据应用中心网站(http://beta.sedac.ciesin.columbia. edu);(6)研究区域沿海各市烟粉尘排放量及汽车拥有量,数据来源于我国国家统计局发布的最新统计年鉴及沿海各省统计年鉴(http://www. stats.gov.cn).以上地图数据处理均基于ArcGis10.2,采用A lbers等面积投影.

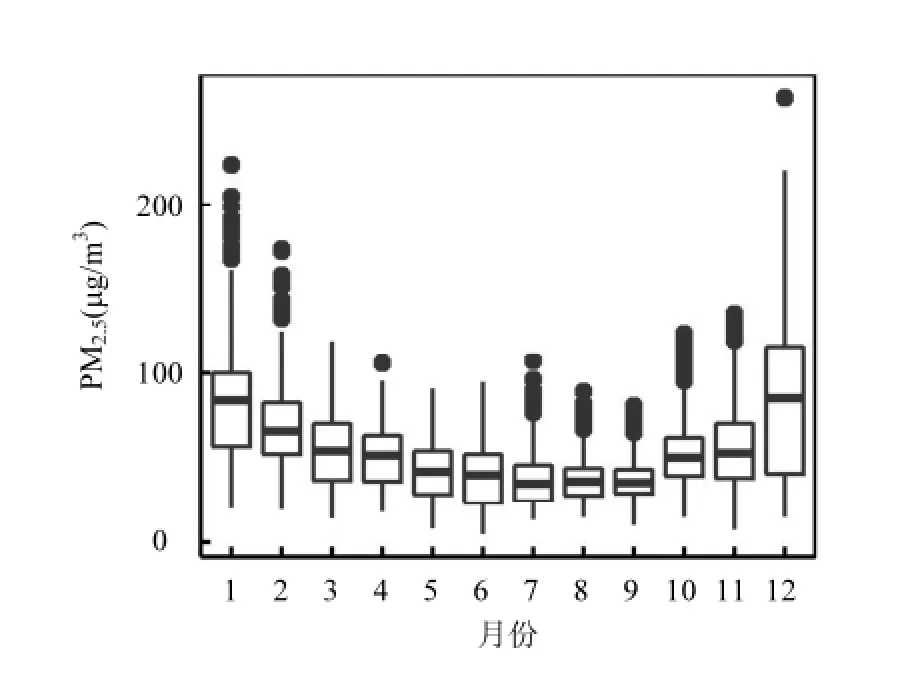
图2 2015年1～12月各站点PM2.5观测浓度Fig.2 Box plot of monthly average concentration PM2.5(fromJan. to Dec. 2015)

1.2 LUR模型

LUR模型的构建主要包括在ArcGis10.2软件中各种变量(variable,以下因子简称v)数据的提取和在SPSS22.0软件中采用逐步多元回归对因子进行筛选.变量的获取过程如下,(1)监测站点处高程值(v1)由ArcGis10.2软件根据站点经纬度提取高程影像值得到;(2)根据海岸线及道路矢量图层计算得到监测站点距海距离(v2)及距主要道路距离(v3)和距次要道路距离(v4);(3)以站点位置为中心设置500m、1km、3km、5km、7km、10km缓冲圆,计算个缓冲圆内道路总长度(v5～v10)及人口密度(v11～v16);(4)由于最终图像分辨率为8km×8km,对于归一化植被指数NDVI取监测站点4km缓冲区内NDVI平均值.模型构建利用数据分析软件SPSS22.0实现,采用逐步多元回归,最终剩余4类因子,多元回归模型如下:

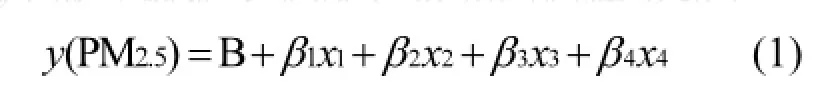
式中:x1代表监测站点所在高程值,km;x2表示监测站点离海岸线距离,km;x3表示5km缓冲区内道路总长度,km;x4表示4km缓冲半径内归一化植被指数NDVI平均值.

1.3 BME时空分析

贝叶斯最大熵(BME)是由George Christakos在1990年提出的一种基于认知学的时空数据分析方法[21-22],其最大的优势在于能够综合利用各种来源不同的不确定性数据,显著地提高未采样点的估计精度[23].

BME方法的实施基于Matlab的Seks-gui时空分析软件包(http://140.112.63.249/SEKSGUI/SEKSHome.html).用一个时空随机场(space/time randomfield, S/TRF)来描述PM2.5的时空变异,用Z(p)=Z(s,t)表示时空随机场中PM2.5的月均浓度,s表示观测点所在经纬度,t表示月份.那么最终PM2.5质量浓度的估计值可由式(2～3)计算得出.

式中:Rs,t表示实际观测值与LUR模型预测值的差值,即残差;Z(s,t)表示最终的预测值, ZLUR(pre)表示LUR模型预测值,Os,t表示实际观测值.

假设LUR模型的残差Rs,t同样能用S/TRF来描述其时空变异,利用BME对其进行时空分析.本研究中,一般知识由时空平均趋势函数mr(p)=E[R(p)]和协方差函数CR(p,p')=E{[R(p)-mr(p)][R(p')-mr(p')]}组成,特定知识由计算各个站点的残差Rs,t组成.BME估计可由式(4)获得:

其中:fG( r)是由一般知识获得的关于r的先验概率密度函数,fk( rk)是r在估计点pk的后验概率密度函数,A是归一化常数.根据后验概率密度函数,可以计算得出r在估计点pk处的估计均值:

式中:rk,mean是r在pk估计点处的估计均值,带回式(3)即可计算得出PM2.5质量浓度的估计值.

2 结果及讨论

2.1 LUR/BME模型

本文LUR模型最终剩余的显著性因子包括高程,距海距离,道路长度,NDVI(表1).高程体现了由于研究区域广阔,地形变换复杂所导致的PM2.5空间分布上的差异性,许多研究表明,一般来说大部分地区高程与PM2.5质量浓度呈负相关[6,24-25],在本文研究区域最终模型也是如此.同时本文研究区域主要是沿海省市,地处海陆交互作用地带,相比于其它内陆地区LUR模型的研究,距海距离在本文最终模型中贡献很大,反映了距海越远,PM2.5质量浓度越高的宏观趋势.而城市微观方面,汽车尾气及工业废气的排放是PM2.5主要来源,由于缺乏具体的排放清单及交通数据,本文以道路长度体现污染源的排放情况,由最终模型参数可知,道路长度与PM2.5质量浓度呈正相关,符合科学认知.但本文LUR模型最终拟合度R2(0.36)小于Reyes等[20]对于全美国PM2.5研究中的LUR模型拟合度R2(0.53),原因之一可能是由于Reyes构建模型中引入了详细的固定点污染源(NOx,SO2,NH3)排放数据及机动车排放数据,而Beckerman等[22]对于全美国PM2.5研究中的LUR模型构建中引入遥感数据,最终拟合度R2(0.21),本文LUR模型R2高于Beckerman的研究,虽然主要原因得益于本文相比于Beckerman的研究区域面积来说较小,但说明本文的模型一定程度上反应了PM2.5的空间分布特征.另一方面许多研究表明植被覆盖即地区的绿化程度对于空气污染具有缓解作用[6,11],最终模型中NDVI与PM2.5质量浓度呈显著负相关.

由于第1阶段的LUR模型不足以充分解释大范围区域PM2.5的时空分布,本文在第2阶段引入BME模型,BME作为一种有效的时空插值方法,能充分考虑空间及时间上的变异(图3),对LUR模型得到的残差进行时空插值,得到全领域残差的时空分布,最后将LUR估测值与BME对残差的估测值相加,得到全领域的PM2.5时空分布.

表1 回归分析参数Table 1 Parameters of correlation analysis

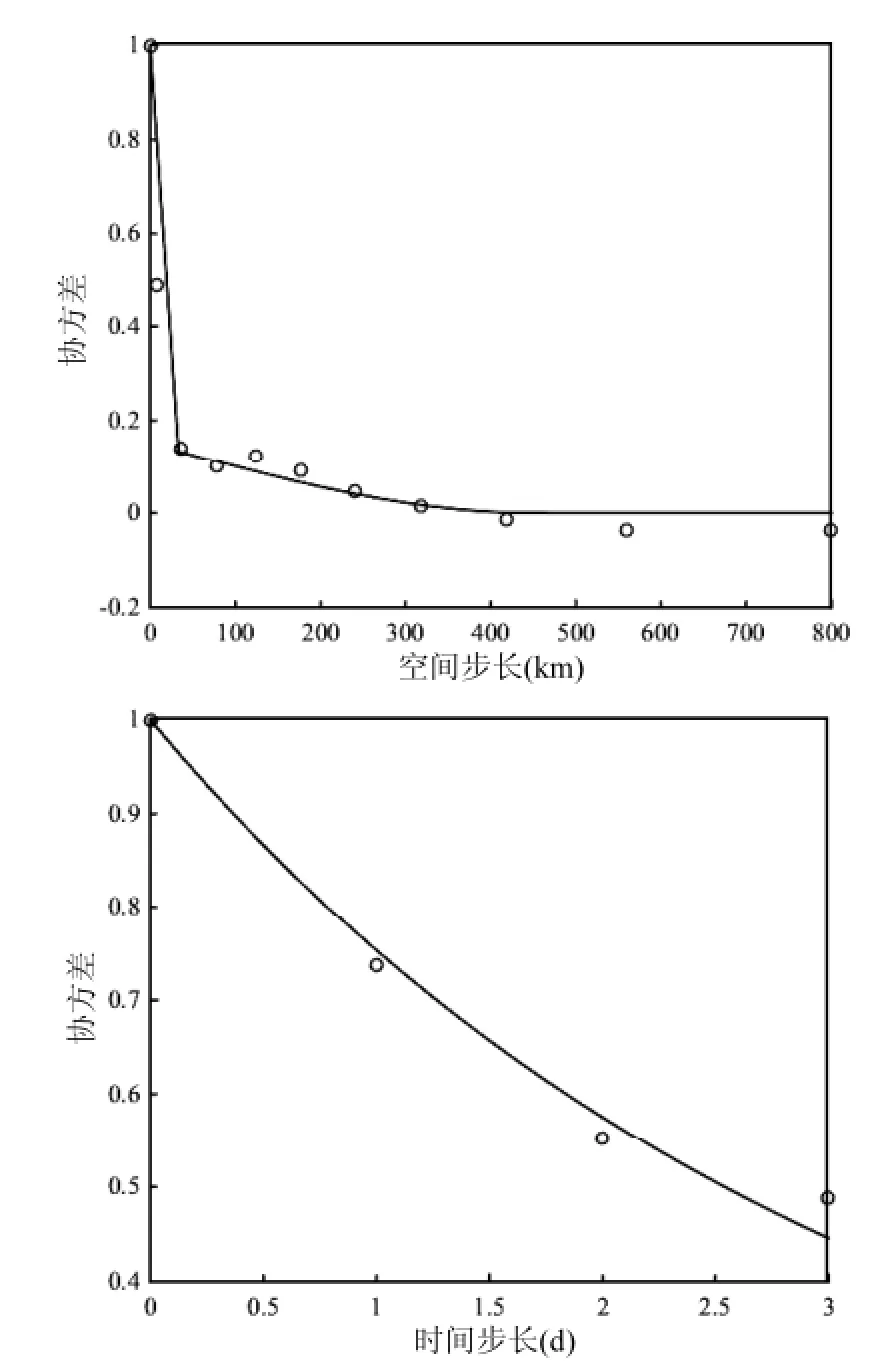
图3 BME模型协方差拟合Fig.3 Covariance model fitting of BME

2.2 海岸带PM2.5时空制图精度及讨论

本文研究区域较广,仅以LUR模型并不能较好的展现全领域污染物分布的特性,且LUR模型在表现时间变异上也较为欠缺,而BME作为科学性的时空数据分析方法则能较好的与LUR相结合.本研究从5376个月平均观测值中抽取1000个真实观测值作为验证,用其他观测值进行模型预测,结果也表明在引入BME后,预测精度得到了显著提高,均方根误差RMSE由23.53µg/ m3降低到11.08µg/m3.Akita等[18]对于西班牙加泰罗尼亚NO2分布估测的研究中也有结论表明LUR相比于传统地统计学(克里金)更加精确.但Akita的研究也表明LUR与其它方法如大气扩散模型等的结合更能全面反映污染物分布的空间变异,而这一点也得到了许多研究的证实[17,20,26-27].同时相较于传统地统计学,该类方法的使用也避免了大范围平滑效应(图3).邹滨等[2]以美国休斯顿为研究区域比较了LUR与普通克里格对PM2.5分布作图的精度,证实LUR模型在预测精度与图像信息熵方面更优于普通克里格.

表2 模型比较Table 2 Comparison between LUR and LUR-BME

图4 2015年沿海部分省份PM2.5质量浓度时空分布Fig.4 Spatiotemporal distribution of PM2.5concentration in Coastal Areas of China, 2015

整体上看(图4),空间尺度上,海岸带PM2.5质量浓度由南至北,以长江三角洲为分界线,宏观上呈现南低北高,京津冀地区作为重点污染地区空气状况仍然形势严峻,河北西南部,山东西部及北京城区属严重污染区域,一方面与该部分地区经济工业发展及气候有关[12],另一方面薛文博等[28]利用颗粒物来源追踪技术PSAT定量模拟我国PM2.5城市来源研究表明,北京,天津及石家庄PM2.5受外省影响较大,分别达37%,42%,33%.而长江三角洲地区2015年PM2.5质量浓度也普遍较高,福建,广东等地空气质量则相对较好.时间尺度上,整个研究区域秋冬2季PM2.5质量浓度普遍偏高,夏季PM2.5质量浓度较低.

本文最终得到的PM2.5质量浓度分布分辨率为8km×8km均匀网格,为比较各市PM2.5污染状况,我们计算各省市行政区划内所有网格平均值代表其四季PM2.5平均质量浓度(图5).各省市四季PM2.5质量浓度差异较大,其中冬季空气污染最为严重,PM2.5质量浓度普遍较高,最高天津市达94µg/m3,最低福建省23.4µg/m3;而各省市夏季PM2.5质量浓度普遍较低,最低福建省7.1µg/m3.

图5 沿海部分省市四季PM2.5平均浓度Fig.5 Seasonal mean PM2.5concentration in Coastal A reas of China, 2015

2.3 山东省空气污染人体暴露研究

山东作为我国北方人口基数较大的省份,其空气污染问题非常严峻[29],为进一步验证本方法的应用价值,本文以山东省为典例将LUR/ BME的空间数据分析方法应用于室外PM2.5人体暴露分析,由于人口普查数据是以行政区划来统计,例如高山,水域等地人口较少,如此不利于计算操作且结果不精确,本文采用第4代全球人口密度1km分辨率栅格数据,通过以下公式计算[6]:

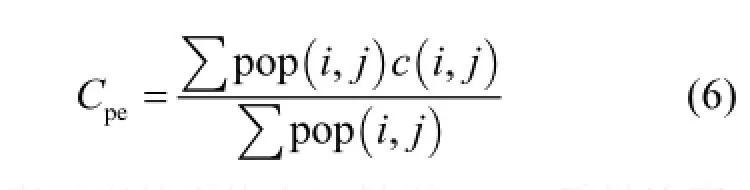
式中:Cpe表示室外平均人口暴露PM2.5质量浓度, µg/m3;pop(i,j)表示第i行第j列栅格代表的人口密度,人/km2;c(i,j)表示第i行第j列栅格代表的PM2.5质量浓度,µg/m3.

山东省年均PM2.5分布呈现明显的阶梯型分布(图6),内陆城市污染严重,而沿海城市则较为改善,以人口密度栅格数据计算人均暴露浓度,减少了PM2.5分布不均而城市地区人口密度较高所产生的误差.

图6 2015年山东省PM2.5年平均浓度空间分布Fig.6 Annual mean PM2.5concentration distribution in Shandong Province, 2015

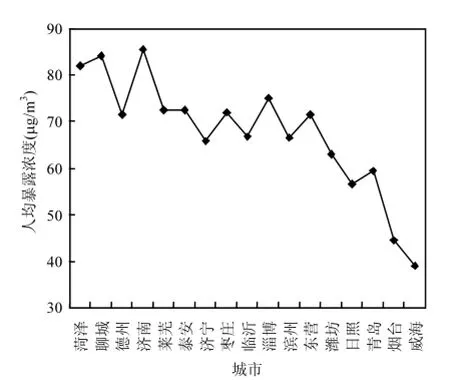
图7 山东省2015年PM2.5人均暴露浓度Fig.7 Per capita outdoor population exposure to PM2.5in Shandong Province, 2015

由内陆至近海,山东省PM2.5人均暴露质量浓度逐步递减(图7),济南市作为山东省会城市,工商业最为发达且人口集中,最高达85.5µg/m3,而近海城市日照,青岛,烟台,威海则相对较低,但大部分人口较为集中的地区仍高于我国现行的PM2.5质量浓度年平均限值35µg/m3.一方面可能与山东内陆及周边城市工厂排放量较高有关,另一方面关于近海气候因素对空气污染的影仍需进一步研究.

3 结论

3.1 本文通过站点实测数据及与空气污染相关的地理因子,采用LUR与BME相结合的空间数据分析方法,得到了海岸带部分地区高精度的PM2.5质量浓度格点分布. 结果显示各省市四季PM2.5质量浓度差异较大,其中冬季空气污染普遍较为严重,PM2.5质量浓度最高为天津市达94μg/m3,最低福建省23.4μg/m3;而各省市夏季PM2.5质量浓度普遍较低,最低福建省7.1μg/m3.

3.2 将该方法应用到山东省PM2.5室外人体暴露分析的结果表明,由内陆至近海人均PM2.5暴露质量浓度逐步递减,最高济南市85.5μg/m3,烟台、威海等沿海城市相对较低.

3.3 由于PM2.5在时间及空间上受许多因素影响,如气象因素,污染源等,本文并未纳入到研究中,导致结果可能受某一因子影响较大,局部出现较大误差,且本文研究是基于月平均PM2.5质量浓度,在后续的研究中可考虑提高时间分辨率[30],或结合遥感数据得到大范围PM2.5高分辨率时空分布.

[1] Yang Y, Christakos G, Huang W, et al. Uncertainty assessment of PM2.5contamination mapping using spatiotemporal sequential indicator simulations and multi-temporal monitoring data [J]. Science Reports, 2016,6:24-35.

[2] Zou B, Luo Y Q, Wan N, et al. Performance comparison of LUR and OK in PM2.5concentration mapping: a multidimensional perspective [J]. Science Reports, 2015,5:86-98.

[3] Lv B, Hu Y, Chang H H, et al. Improving the Accuracy of Daily PM2.5Distributions Derived fromthe Fusion of Ground-Level Measurements with Aerosol Optical Depth Observations, a Case Study in North China [J]. Environmental Science & Technology, 2016,50(9):4752-4759.

[4] Zhang W, Capps S L, Hu Y, et al. Development of the high-order decoupled direct method in three dimensions for particulate matter: enabling advanced sensitivity analysis in air quality models [J]. Geoscientific Model Development Discussions, 2011,4(4):355-368.

[5] 焦利民,许 刚,赵素丽,等.基于LUR的武汉市PM2.5浓度空间分布模拟 [J]. 武汉大学学报(信息科学版), 2015,40(8):1088-1094.

[6] Wu J S, Li J C, Peng J, et al. Applying land use regression model to estimate spatial variation of PM2.5in Beijing, China [J]. Environmental Science Pollution Research, 2015,22(9):7045-7061.

[7] Briggs D J, Collins S, Elliott P, et al. Mapping urban air pollution using GIS: a regression-based approach [J]. International Journal of Geographical Information Science, 1997,11(7):699-718.

[8] Henderson S B, Beckerman B, Jerret M, et al. Application of land use regression to estimate long-termconcentrations of traffic-related nitrogen oxides and fine particulate matter [J]. Environmental Science & Technology, 2007,41(7):2422-2428.

[9] Miyawaki J, Kamei S, Sakayama K, et al. Modeling the Intraurban Variability of Ambient Traffic Pollution in Toronto, Canada [J]. Journal of Toxicology & Environmental Health Part A, 2007,70(3/4):200-212.

[10] Beckerman B S, Jerrett M, Martin R V, et al. Application of the deletion/substitution/addition algorithmto selecting land use regression models for interpolating air pollution measurements in California [J]. Atmospheric Environment, 2013,77(68):172-177.

[11] Hassan A, Seyed Mahmood T S, Henderson S B, et al. Land use regression models to estimate the annual and seasonal spatial variability of sulfur dioxide and particulate matter in Tehran, Iran. [J]. Science of the Total Environment, 2014,489(488-489C): 343-353.

[12] 陈 莉,白志鹏,苏 笛,等.利用LUR模型模拟天津市大气污染物浓度的空间分布 [J]. 中国环境科学, 2009,29(7):685-691.

[13] Li C, Du S Y, Bai Z P, et al. Application of land use regression for estimating concentrations of major outdoor air pollutants in Jinan, China [J]. Journal of Zhejiang University-SCIENCE A, 2010, 11(11):857-867.

[14] Liu W, Li X, Chen Z, et al. Land use regression models coupled with meteorology to model spatial and temporal variability of NO2, and PM10, in Changsha, China [J]. A tmospheric Environment, 2015,116:272-280.

[15] Liu C, Henderson B H, Wang D, et al. A land use regression application into assessing spatial variation of intra-urban fine particulate matter PM2.5and nitrogen dioxide NO2concentrations in City of Shanghai, China. [J]. Science of the Total Environment, 2016,565:607-615.

[16] Akita Y, Baldasano J M, Beelen R, et al. Large scale air pollution estimation method combining land use regression and chemical transport modeling in a geostatistical framework. [J]. Environmental Science & Technology, 2014,48(8):4452-4459.

[17] Yu H L, Wang C H, Liu MC, et al. Estimation of Fine Particulate Matter in Taipei Using Landuse Regression and Bayesian MaximumEntropy Methods [J]. International Journal ofEnvironmental Research & Public Health, 2011,8(6):2153-2169.

[18] Reyes J, Serre ML. An LUR/BME Framework to Estimate PM2.5Explainedby on Road Mobile and StationarySources [J]. Environmental Science & Technology, 2014,48(3):1736-1744.

[19] Matheron G. The Theory of Regionalized Variables and Its Application [J]. 1971,5:218.

[20] Beckerman B S, Jerrett M, Serre M, et al. A Hybrid Approach to Estimating National Scale Spatiotemporal Variability of PM2.5in the Contiguous United States [J]. Environmental Science & Technology, 2013,47(13):7233-7241.

[21] Christakos G. A Bayesian maximum-entropy viewto the spatial estimation problem[J]. Mathematical Geosciences, 1990,22(7): 763-777.

[22] Christakos G, Serre ML. BME analysis of spatiotemporal particulate matter distributions in North Carolina [J]. Atmospheric Environment, 2000,34(20):3393-3406.

[23] 杨 勇,张若兮.贝叶斯最大熵地统计方法研究与应用进展 [J].土壤, 2014(3):402-406.

[24] Henderson S B, Beckerman B, Jerrett M, Brauer M. Application of Land Use Regression to Estimate Long-TermConcentrations of Traffic-Related Nitrogen Oxides and Fine Particulate Matter [J]. Environmental Science & Technology, 2007,41(7):2422-2428.

[25] Hart J E, Yanosky J D, Puett R C, et al. Spatial Modeling of PM10and NO2in the Continental United States, 1985～2000 [J]. Environmental Health Perspectives, 2009,117(11):1690-1696.

[26] Wang M, Sampson P D, Hu J, et al. Combining Land-Use Regression and Chemical Transport Modeling in a Spatiotemporal Geostatistical Model for Ozone and PM2.5. [J]. Environmental Science & Technology, 2016,50(10):5111-5118.

[27] Bechle MJ, Millet D B, Marshall J D. National Spatiotemporal Exposure Surface for NO2: Monthly Scaling of a SatelliteDerived Land-Use Regression, 2000～2010. [J]. Environmental Science & Technology, 2015,49(20):12297-12305.

[28] 薛文博,付 飞, 王金南,等.中国PM2.5跨区域传输特征数值模拟研究 [J]. 中国环境科学, 2014,34(6):1361-1368.

[29] Yang Y, Christakos G. Spatiotemporal Characterization of Ambient PM2.5Concentrations in Shandong Province (China). [J]. Environmental Science & Technology, 2015,49(22):13431-13438.

[30] 郭 宇,邹 滨,郑 忠,等.高时空分辨率PM2.5浓度土地利用回归模拟与制图 [J]. 遥感信息, 2015(5):94-101.

Spatiotemporal analysis of PM2.5in large coastal domains by combining Land Use Regression and Bayesian MaximumEntropy.

JIANG Qu-tu1, HE Jun-yu1, WANG Zhan-shan2, YE Guan-qiong1*, CHEN Qian3, XIAO Lu1
(1.Institute of Island & Coastal Ecosystems, Zhejiang University, Zhoushan 316021, China；2.Beijing Municipal Environmental Monitoring Center, Beijing 100048, China；3.School of Geographic and Environment, Jiangxi Normal University, Nanchang 330022, China). China Environmental Science, 2017,37(2)：424～431

By combining Land Use Regression (LUR) and Bayesian MaximumEntropy (BME), this study constructed a LUR model based on the parameters of elevation, distance to sea, length of roads and Normalized Difference Vegetation Index (NDVI) to generate a global map of PM2.5distribution in a large costal area in 2015, china. The Bayesian MaximumEntropy was further introduced in the interpolation of LUR space-time residuals. Because of the introduction of BME, the cross-validation results showed that the R2increased from0.36 to 0.85, and the root-mean-square error (RMSE) decreased from23.53µg/m3to 11.08µg/m3. The average concentration of PM2.5in the northern coastal areas was higher than that of the southern areas, and the highest concentration of PM2.5appeared in the inland area of Beijing, Tianjin, Hebei and Shandong provinces during winter times. The annual spatial distribution of PM2.5was further integrated with population density in Shandong province for risk exposure analysis. The outcome showed that the outdoor population exposure of PM2.5decreased frominland to sea, and the highest Per capita outdoor exposure value occurred in the central city, Jinan (85.5µg/m3), while the lowest value occurred in coastal areas of Yantai and Weihai.

land use regression；bayesian maximumentropy；PM2.5；human exposure

X51

A

1000-6923(2017)02-0424-08

江曲图(1992-),男,湖北咸宁人,浙江大学海洋学院硕士研究生,主要从事海岸带环境健康研究.

2016-06-18

科技部国际合作项目(2015DFA01410)

* 责任作者, 讲师, gqy@zju.edu.cn