基于改进量子粒子群算法的电力系统经济调度仿真研究

陈功贵, 黄山外, 孙 智, 张治中, 熊国江

(1. 重庆邮电大学 自动化学院, 重庆 400065； 2. 国电恩施水电开发有限公司, 湖北 恩施 445000；3. 重庆邮电大学 通信网与测试技术重点实验室, 重庆 400065；4贵州电网有限责任公司电力调度控制中心, 贵州 贵阳 550002)

虚拟仿真技术探索与实践

基于改进量子粒子群算法的电力系统经济调度仿真研究

陈功贵1, 黄山外1, 孙 智2, 张治中3, 熊国江4

(1. 重庆邮电大学 自动化学院, 重庆 400065； 2. 国电恩施水电开发有限公司, 湖北 恩施 445000；3. 重庆邮电大学 通信网与测试技术重点实验室, 重庆 400065；4贵州电网有限责任公司电力调度控制中心, 贵州 贵阳 550002)

针对水火电系统的多约束、时滞非线性特点,建立了带有梯级水电厂的电力系统模型,并采用量子粒子群(QPSO)算法对系统进行优化求解。为了解决基本量子粒子群算法容易陷入局部最优解的问题,提出了一种改进量子粒子群(IQPSO)算法。为了验证该算法的性能,运用Matlab编写程序,利用典型的4水电3火电系统算例进行仿真。算例表明,改进的量子粒子群算法具有更好的收敛特性。

电力系统； 经济调度仿真； 量子粒子群算法； Matlab

水火电调度对于电力系统稳定、经济地运行十分重要。短期水火电调度的目的是在一天的总调度周期内,在满足各种等式和不等式约束的条件下,寻求水电厂的最优水排量和火电厂的最优发电功率,使得总的目标函数最小[1]。实际发电过程中的等式约束包括系统的符合平衡和水库的初末端库容平衡；不等式约束包括水电厂和火电厂的输出功率限制、水库的最大库容限制和水排放限制。除此之外,还应考虑火电厂的阀点效应[2]、网络的传输损耗[3]、禁止排放区等附加因素[4]。因此,短期水火电调度问题是一个典型的非凸非线性优化问题。

量子粒子群(quantum-behaved particle swarm optimization,QPSO)算法是一种基于粒子随机性搜索的智能算法,已经广泛应用于各种优化问题中[5-6]。但是,在面对复杂的非线性水火电优化调度问题时,量子粒子群算法不能保证全局收敛,容易陷入局部最优解[7]。笔者采用指数下降型收缩-扩张系数对传统的量子粒子群算法进行改进,以平衡量子粒子群算法的全局搜索能力和局部搜索能力。为了验证该算法的有效性,运用Matlab软件编写程序,并采用包含4个水电厂和3个火电厂的典型算例进行仿真研究。实验结果表明,所提出的改进量子粒子群算法仿真速度更快、解的质量更好。

Matlab软件提供了用于算法开发、数据可视化、数据分析以及数值计算的高级计算语言和交互式环境[8-11],其强大的可视化图形能够使学生直观认识改进量子粒子群算法仿真曲线,更有助于实验教学。

1 水火电系统数学模型

水火电经济调度的总目标是在满足所有约束条件的情况下,充分利用水资源、最大限度降低火电厂的发电量,从而使得火电厂的燃料费用最小。其目标函数可以表示为

(1)

式中:Fmin表示最小总成本；T为总调度周期；Ns为火电厂总个数；as,i,bs,i,cs,i为第i个火电厂的燃料费用系数；Ps，i,t表示t时段第i个火电厂的发电量。在短期水火电调度问题中,总调度周期为1天(24 h),调度的时间间隔为1 h。

1.1 等式约束

(1) 系统负荷平衡约束为

(2)

其中:Ph,j,t为第j个水电厂t时段的发电量,是关于排水量和库容的二次函数；PD,t为t时段的负荷所需发电量。

(2) 水动态平衡约束为

(3)

其中:Vj,t为第j个水库在t时刻的库容；Ij,t表示第j个水库在t时刻水的自然流入量；Qj,t表示第j个水库在t时刻的排水量，Nj为与该水库相连的上游水库的个数；τ表示水从上游水库流到下游水库的时间。

1.2 不等式约束

(1) 水电厂输出功率约束为

(4)

(2) 火电厂输出功率约束

(5)

(3)水库库容约束

(6)

(4) 水库水排量约束

(7)

其中:Ph，j,min和Ph，j,max分别是第j个水电厂输出功率的下限值和上限值；Ps，i,min和Ps，i,max分别是第i个火电厂输出功率的下限值和上限值；Vj,min和Vj,max分别是第j个水库容量的下限值和上限值；Qj,min和Qj,max分别是第j个水库排水量的下限值和上限值。

2 量子粒子群算法

2.1 量子粒子群算法的数学模型

量子粒子群(QPSO)算法是孙俊等人在研究了粒子的运动轨迹后提出的一种全局性启发式算法[12]。在QPSO算法中,假设有N个粒子在一个D维的量子空间运动,粒子的位置可以表示为xi=[xi1,xi2,…,xiD]T,(i=1, 2,…,N)。在粒子的搜索过程中,已经搜索到的最好适应度值所代表的位置为粒子的个体最优位置Pi=[Pi1,Pi2,…,PiD]T；在某次搜索中,所有粒子的最好适应度值所代表的位置为全局最优位置PG=[PG1,PG2,…,PGD]T。为了让群体处于聚集状态,产生一个局部吸引子pi来保证粒子能达到全局收敛，其定义如下:

(8)

其中:φ为0到1之间的随机数。根据蒙特卡洛规则,可以得到第k+1代粒子的位置更新公式为

(9)

其中k表示迭代次数；u为0～1之间的随机数；β表示收缩扩张系数,可以表示为:

(10)

βmax与βmin分别为迭代初期和达到最大迭代次数时的收缩扩张系数,通常取βmax为1,βmin为0.5；kmax为最大迭代次数。Mbest表示所有粒子个体最优位置的平均值,即:

(11)

QPSO算法具有以下特点[13]:(1)算法模型简单,量子系统中不存在速度矢量；(2)理论上粒子可以搜索到任何位置而达到全局收敛；(3)迭代过程中的控制参数只有一个。

2.2 量子粒子群算法的改进

量子粒子群算法由于其控制参数少,且能保证全局收敛而被广泛应用。但是,它在处理高维、复杂、非线性问题时容易陷入局部最优解。因此,本文引入一种指数下降型的收缩-扩张系数来增强算法的搜索性能,其表达式为:

(12)

其中βini表示迭代初始的收缩扩张系数,通常设置为1；n为非线性变化规律的控制幂指数。分析公式(12)可以看出,确定好参数βini和kmax后,无论幂指数n取何值,β的值始终由βini开始呈指数型下降趋势到e-1。

2.3 IQPSO算法优化水火电调度模型

为了充分降低电力系统运行成本,本文在已经建立的水火电调度模型的基础上,运用改进量子粒子群(improved quantum-behaved particle swarm optimization,IQPSO)算法对模型的参数进行优化,优化步骤如下:

(1) 种群初始化。在可行域内随机产生N个粒子,每个粒子包含Nh个水电厂T个时段的排水量参数Q和Ns个火电厂T个时段的发电量参数Ph,初始化算法中的各个参数，迭代次数k和最大迭代次数kmax。

(2) 约束处理。先引入排水量参数Q,通过公式(3)来调整粒子的位置,使得每个粒子满足水动态平衡约束,并计算水电厂发电量。接着在负荷平衡公式(4)中引入火电厂的发电量参数Ph,继续调整粒子的位置,使得每个粒子满足系统负荷平衡。通过目标函数(公式(1))计算每个粒子的适应度值,更新粒子的个体最优值pbest和全局最优值gbest。

(3) 位置更新。根据公式(9)更新每个粒子的位置,并根据步骤(2)来获得满足约束条件的粒子。

(4) 更新个体最优值。再次计算粒子适应度值,如果当前粒子适应度值比个体最优适应度pbest小,则将当前粒子适应度值赋值给pbest。

(5) 更新全局最优值。如果第k代所有粒子全局最优适应度值比全局最优适应度gbest小,则将当前群体全局最优适应度值赋值给gbest。

(6) 判断循环或停止。若当前迭代次数k小于kmax,则k=k+1,跳转程序到步骤(3)；否则停止循环并输出最优解。

3 基于Matlab的经济调度仿真实验

运用所提出的算法建立了水火电调度模型,并对含有4个水电厂和3个火电厂的电力系统进行优化调度。总调度周期为24 h,每1 h为1个时段,24 h的负荷需求和发电厂参数分别在表1和表2中给出。

表1 负荷需求 MW

表2 水电厂参数

分别运用PSO、QPSO和IQPSO算法对测试系统进行优化。为保证实验的客观性,所有算法采用相同的参数设置,其中种群数量设置为50,迭代次数设置为1 500,仿真实验总次数设置为20。

基于以上参数设置,在Matlab中编写程序进行仿真,记录3种算法1 500次迭代过程中燃料费用的最优值、最差值、平均值以及平均仿真时间(见表3)。

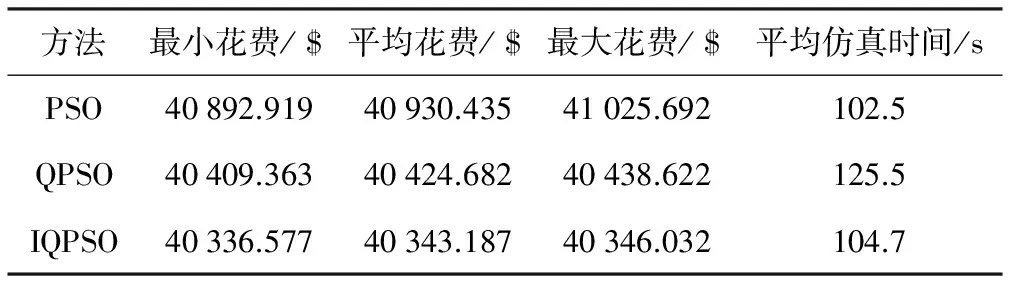
表3 三种算法的燃料费用及仿真时间对比

从最小花费来看,与PSO和QPSO算法相比,改进后的IQPSO算法得到的目标函数值最小；从算法的鲁棒性来看,由IQPSO算法得到的仿真结果与其他两种算法相差不大,但更加稳定；从平均仿真时间上来看,PSO算法和IQPSO算法的仿真时间相差不大,但与QPSO算法相比有明显减少。

图1给出了3种算法20次仿真实验得到的最优结果的收敛曲线。从曲线中可以看出,IQPSO算法的收敛性能得到了改善。当迭代次数为1 000时,其目标函数值已经稳定,算法达到全局收敛,而另外两种算法还没有达到收敛。图2和图3分别给出了IQPSO算法求得的最优水库库容曲线和功率平衡曲线。图2说明整个系统满足水的动态平衡约束,图3说明系统满足负荷平衡约束。

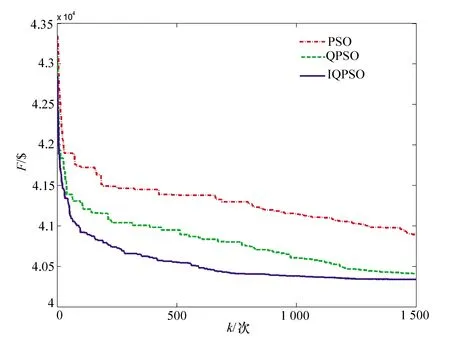
图1 PSO、QPSO和IQPSO收敛曲线

图2 IQPSO算法得到的最优水库库容曲线

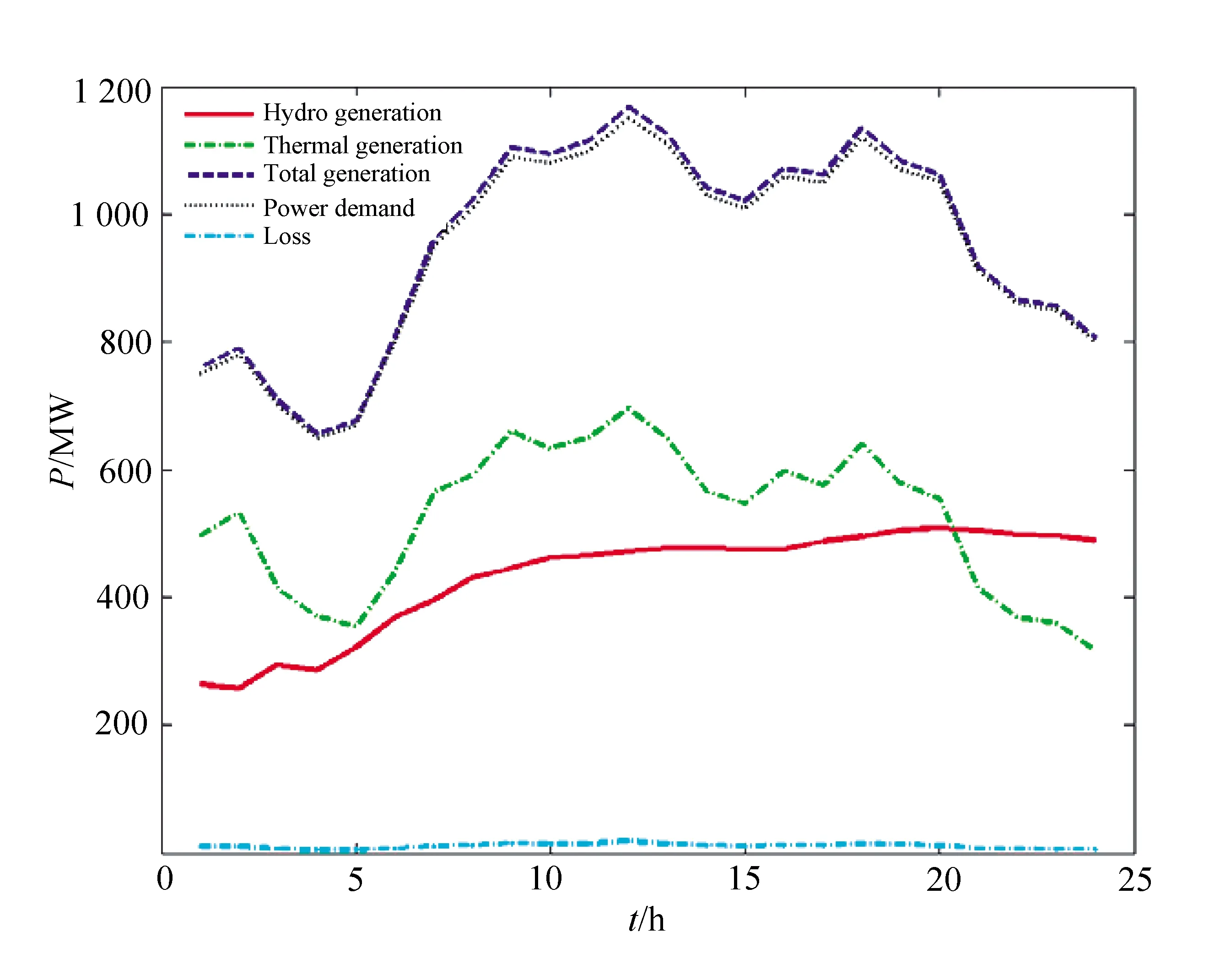
图3 IQPSO算法得到的负荷平衡曲线

4 结语

本文以燃料费用最小为目标函数,建立了一个复杂、非线性的水火电系统模型,并提出一种改进的量子粒子群算法来解决电力系统水火电优化调度问题。在QPSO算法的基础上,引入一个指数下降型收缩扩张系数,使得算法在全局搜索和局部搜索之间得到平衡。利用Matlab工具对一个典型的系统模型进行仿真实验。从实验数据和图形可以直观地看出,所提出的改进量子粒子群算法能够得到高质量的解,且表现出更好的鲁棒性。这种将实验结果图形化的方式能够使学生充分认识电力系统经济调度模型,也能有效地促进关于电力系统经济调度的教学工作。

References)

[1] 雷绍林,秦珍.水火电力系统短期节能与经济发电优化调度[J].现代电力,2012,29(5):50-54.

[2] 董佳瑞,郑垂勇,李致家,等.计及阀点效应负荷经济分配的SCE-UA算法[J].水力发电学报,2014,33(4):277-285,294.

[3] 赵维兴,林成,孙斌,等.安全约束条件下综合煤耗最优的节能调度算法研究[J].电力系统保护与控制,2010,38(9):18-22.

[4] 张世翔,烧慧壮.含风电的电力系统低碳经济调度[J].工业安全与环保,2016,42(5):92-95.

[5] 李仁府,独孤明哲,胡麟,等.基于QPSO算法移动机器人轨迹规划与实验[J].控制与决策,2014,29(12):2151-2157.

[6] 张宏立,李瑞国,范文慧,等.基于量子粒子群的全参数连分式混沌时间序列预测[J].控制与决策,2016,31(1):52-58.

[7] 黄为勇,徐晓菊,潘晓博,等.量子粒子群优化算法的收缩-扩张系数控制策略研究[J].计算机应用研究,2016,33(9):2592-2595.

[8] 何德峰,俞立,徐建明.基于MATLAB的现代控制理论实验教学实践[J].实验技术与管理,2016,33(3):123-126.

[9] 陈功贵,刘利兰,郭艳艳,等.基于改进引力搜索算法的无功优化仿真研究[J].实验技术与管理,2016,33(5):113-116,120.

[10] 范孟豹,吴根龙,王禹桥,等.基于PSO的抗扰动最少拍控制器设计[J].实验技术与管理,2016,33(4):38-42,49.

[11] Chen Gonggui, Liu Lilan, Song Peizhu, et al. Chaotic improved PSO-based multi-objective optimization for minimization of power losses and L index in power systems[J].Energy Conversion and Management,2014(86):548-560.

[12] Sun J, Xu W, Feng B. A global search strategy of quantum-behaved particle swarm optimization[J].IEEE Conference on Cybernetics & Intelligent Systems, 2005, 1(11):111-116.

[13] 方伟,孙俊,谢振平,等.量子粒子群优化算法的收敛性分析及控制参数研究[J].物理学报,2010,59(6):3686-3694.

Research on simulation of economic dispatch in power system based on improved QPSO algorithm

Chen Gonggui1, Huang Shanwai1, Sun Zhi2, Zhang Zhizhong3, Xiong Guojiang4

(1. College of Automation, Chongqing University of Posts and Telecommunications, Chongqing 400065,China;2. Guodian Enshi Hydropower Development Corporation, Enshi 445000,China; 3. Key Laboratory of Communication Network and Testing Technology, Chongqing University of Posts and Telecommunications, Chongqing 400065,China；4. Guizhou Electric Power Grid Dispatching and Control Center, Guiyang 550002, China)

Aiming at the multi-constraint, nonlinear delay characteristics of hydrothermal systems, the hydrothermal power system model with a cascade of hydropower plants is established and quantum-behaved particle swarm optimization (QPSO) algorithm is implemented to optimize the system. However, the basic QPSO algorithm is easy to fall into the local optimal solution. Hence an improved QPSO optimization is proposed. In order to verify the performance of the algorithm, codes are written by using Matlab and a typical four-hydropower three-thermal power system is used for simulation. The simulation results show that the improved IQPSO algorithm has better convergence characteristics than those of PSO and QPSO. Using the Matlab simulation in teaching, students can not only strengthen the power system economic operation theory, but also helpf their programming techniques.

power system; simulation of economic dispatch; quantum-behaved particle swarm optimization; (QPSO) algorithm; Matlab

10.16791/j.cnki.sjg.2017.03.026

2016-09-02

国家自然科学基金项目(61463014)；重庆高校创新团队项目(KJTD201312)；重庆邮电大学教育教学改革项目(XJG1416)

陈功贵(1964—),男,重庆,博士,教授,主要从事电气工程专业的教学和科研工作.

E-mail：chenggpower@126.com

TM61; G434

A

1002-4956(2017)3-0104-04