可用于工程教育认证的统计结果可视化新方法*
2017-04-07郭斯羽孟志强
郭斯羽,孟志强,汪 沨,温 和,王 华
(湖南大学 电气与信息工程学院,湖南 长沙 410082)
可用于工程教育认证的统计结果可视化新方法*
郭斯羽,孟志强,汪 沨,温 和,王 华
(湖南大学 电气与信息工程学院,湖南 长沙 410082)
工程教育认证正日益成为众多工科专业的一项常态化的工作。在工程教育认证中,毕业要求达成度评价往往是数据处理和分析任务最为繁重的一个环节。为了有效集约地展示与毕业要求达成度评价有关的统计数据,以便于分析评价结果并用于专业的持续改进,提出了称为塔带图的统计数据可视化方法。塔带图可作为一种有效的可视化工具,用于工程教育认证中统计数据的展示。
数据可视化;统计数据;塔带图;工程教育认证
随着2016年6月2日我国正式加入《华盛顿协议》组织,我国的工程教育认证工作进入了一个新的阶段。[1]工程教育认证为工程教育国际互认和工程师资格国际互认的实现提供了重要基础,而且除了满足工程师人才跨国流动的需求之外,工程教育认证还是工程教育改革与工程教育质量保障体系完善的重要推动力。
一、毕业要求达成度评价中对数据统计分析的需求
在认证工作中,毕业要求达成度的评价往往是涉及数据、计算、统计和分析最多的一个部分,例如在毕业要求达成度评价报告中,通常都会提供包括全体毕业生的各门课程的各考核环节的成绩与总评成绩,以及在各项毕业要求上的达成度。在2016年的工程教育认证标准中包含了12条通用毕业要求,各专业在制定本专业的毕业要求时,必须完全覆盖12条通用要求,因此通常专业的毕业要求数量少至7条,多的可能略多于标准的12条。[2]另外,根据工程教育认证的要求,专业需要将每条毕业要求进一步细化为若干具有可操作性的指标点,从而使需要进行评价的点扩充至数十个。可见,这些学业成绩的分析和呈现以及毕业要求指标点的达成度的计算、分析和呈现形成了认证工作所面临的一个重要挑战。
根据工程教育认证的理念,对于专业而言,要求其每一届毕业生均全部达成所有毕业要求,因此仅仅从考核毕业生的“合格”与否的角度出发,在进行评价时,只需要根据每届毕业生中毕业要求达成度最低的那一个人来进行评判即可。但是毕业要求达成度评价的结果同时也应当应用于专业的持续改进,因此仅靠上述的单个最低达成度显然无法合理体现与衡量专业的整体教学质量与培养质量。为了达到分析整体教学质量的目的,通常可以使用以下方式:
(1)学生的学业成绩和毕业要求达成度的区间分布。成绩或达成度的区间分布就是统计出全体学生中,得分或达成度落在各个区间中的人数,或将人数折算为比例值。区间分布实际上可以视为全体学生的相应指标的直方图分布,从中可以直观地了解学生所取得的指标值的集中分布范围,并据此判断学生在指标上的总体水平。
(2)学生的学业成绩和毕业要求达成度的排序统计量。最典型也最常用的排序统计量是全体学生在某个指标上取得的中值,但如果再进一步配合上最大值、最小值、75%分位值和25%分位值等统计量,则可以更好地反映学生在该指标上的总体水平以及该指标对学生水平的区分能力。
(3)学生的学业成绩和毕业要求达成度的算术均值和样本标准差。它们也同样可以用来反映学生在某个指标上的总体水平及指标的区分能力,而且当建设学生的指标值服从正态分布时,这两个统计量就完全确定了具体的分布。
二、用于统计数据可视化的塔带图
上述各类统计量都已具有常用的可视化方法。区间分布一般可利用柱状图来呈现,但是如果希望在一幅图中同时呈现学生在若干个指标上的区间分布,例如同时呈现学生在若干门课程上取得的总评成绩或是在某个毕业要求的各个指标点上的达成度,则柱状图便不太适用,特别当指标数量较多时,就难以用一幅柱状图来给出图形。而在多个指标上的排序统计量和均值与标准差的数据可以通过曲线图来呈现,不过如果同时在一幅图中给出这些,则曲线数量较多,略显杂乱。此外,排序统计量也可利用桶状图来显示。此外,也可以使用诸如雷达图[3]、玫瑰图[4]等可视化方法来呈现。但这些已有的方法均难以在一幅图形中将上述所有数据都清晰加以展示。
由于上述统计数据各有其优越性与局限性,能够体现出学生整体水平的不同方面,因此,我们希望能够有一种直观的、更为清晰的可视化方式,能够集约地在一幅图形中同时呈现所有这些统计数据。为此设计了我们称之为“塔带图”的一种统计数据可视化图形,介绍如下。
1.塔带图坐标轴的基本构成
塔带图的横轴对应于需要进行统计分析的各个指标项,如若干门课程或若干项毕业要求,纵轴则对应于指标值。由于对于所有指标项,我们都使用同一个纵轴来定位其指标值,因此这隐含地要求所有指标项的取值范围应当是一致的,或者通过某种归一化方法被调整为一致。例如对于课程而言,指标值通常就是原始或折算而得的百分制成绩,而对于达成度,指标值取值范围通常设置为[0,1]。同时,根据区间分布统计的需要,纵轴被相应地分为若干区间,通过纵轴刻度来表示。对于百分制成绩,通常可分为 [0,60)、[60,70)、[70,80)、[80,90)和[90,100]等5个区间,分别对应于“不及格”、“及格”、“中等”、“良好”和“优秀”这5个等级。对于[0,1]区间取值的达成度,也可类似加以划分。
2.排序统计量的可视化
指标值的排序统计量在塔带图中以“带”来表示:将全体学生在各个指标项上取得的最大值和最小值分别依次连成折线,上下两条折线间以颜色填充,即可获得用于表示全体学生在所有指标项上的总体取值范围的条带;类似地,将全体学生在各个指标项上的75%分位值和25%分位值也分别依次连成折线,其间以另一种颜色填充,即可获得用于表示表现居中的半数学生在所有指标项上的取值范围的条带;全体学生在各个指标项上的中值以一条折线表示。需要注意,由于25%-75%分位值范围被包含于最小值、最大值范围之内,因此在绘图时,前者对应的条带应该“覆盖”于后者之上。
3.区间统计量的可视化
指标值的区间统计在塔带图中以圆盘表示。例如有比例为r的学生在指标项A上取得了属于“良好”区间的成绩,则在横坐标对应于指标项A、纵坐标对应于“良好”的取值范围的位置,以一个面积与r成正比的圆盘来加以表示。学生在一个特定的指标项上获得的区间分布便可以通过上下依次排列的一系列圆盘来表示,状如圆塔,结合表示排序统计量的“带”,这便是“塔带图”命名的由来。对于每个指标值区间,可使用的特定颜色来填充与之对应的各个圆盘,以便区分。在绘图时,区间统计圆盘应“覆盖”在排序统计量的条带之上,但不应覆盖中值折线。
4.均值/标准差的可视化
全体学生在各指标项上取得的算术均值μ以特殊的记号如圆点、小圆圈或星形等表示,并以折线相连。各指标项的指标值样本标准差σ利用由均值点朝上、下方发出的钉形表示,上、下钉形所确定的取值范围即为[μσ,μ+σ]区间。
三、塔带图应用示例
下面通过举例来说明塔带图的绘制和解释。
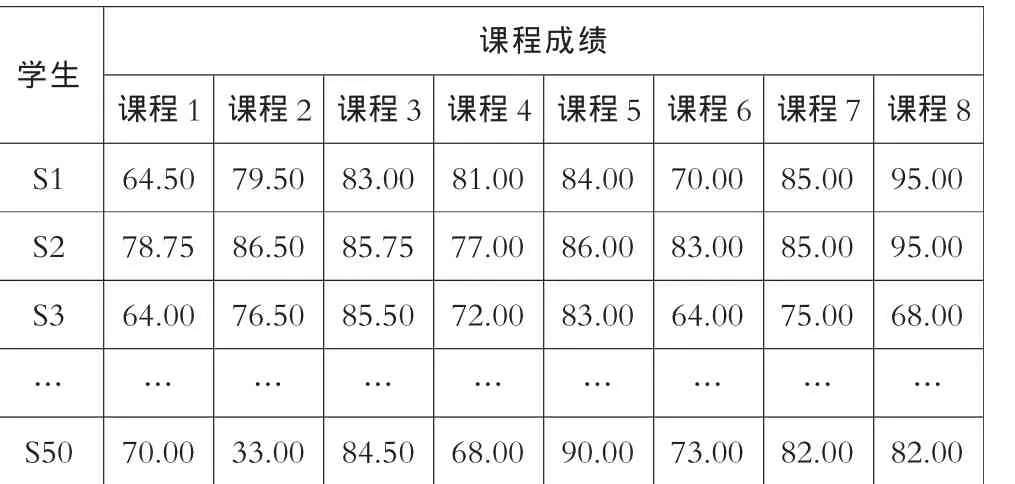
表1 示例中的学生课程成绩
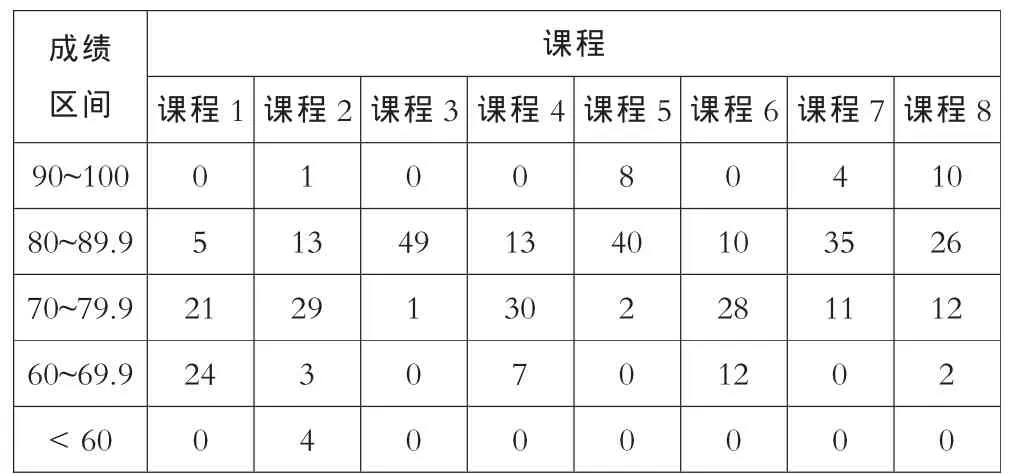
表2 示例学生成绩的区间分布
表1中所列是某一个毕业班全体50名学生在某类共8门课程上所获得的总评成绩。根据成绩进行区间统计、排序统计和均值/标准差求取后所得的结果分别见表2和表3。
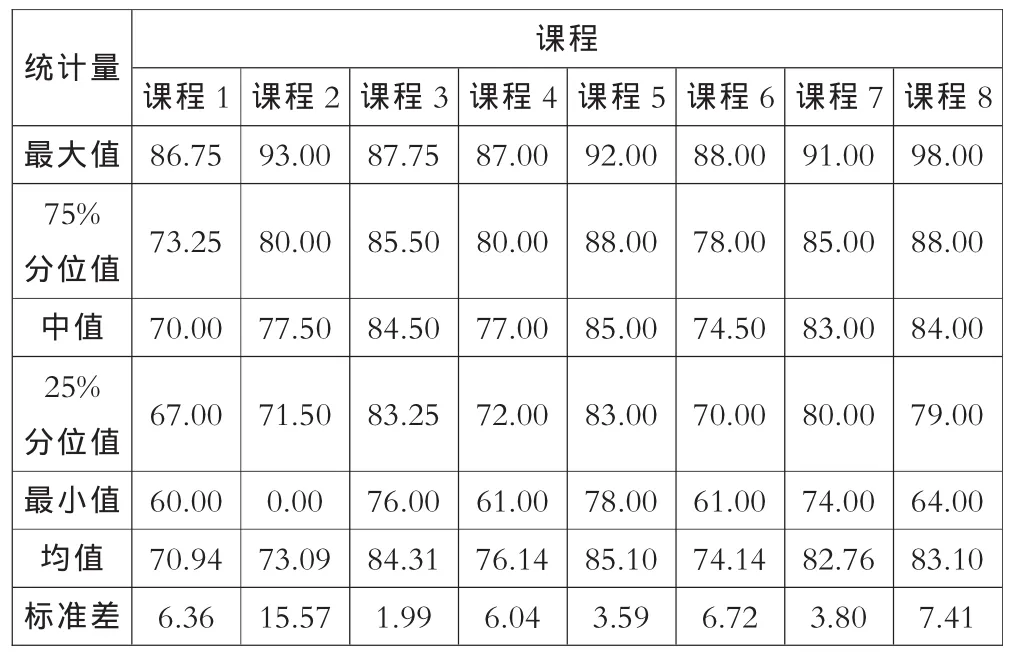
表3 示例学生成绩的排序统计、均值及样本标准差
根据计算结果绘制的塔带图如图1所示。
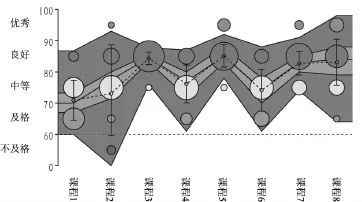
图1 根据示例数据所绘的塔带图
由图1可见,在这8门课程中,总体成绩较好的课程是课程3和课程5,其平均成绩和成绩中值都达到了85分左右;课程3、课程5、课程7和课程8的得分都主要集中在良好这一档,而且在课程5和课程8中还有相当比例的学生取得了优秀的成绩;如果利用排序统计量来考察区分度,则课程3的区分度最低,课程5的区分度也不高,而课程2和课程8的区分度较高;类似地,课程2和课程8的成绩散布范围最大,课程1、课程4和课程6的散布范围次之;从均值和标准差来分析,课程2的标准差最大,但是通过观察成绩分布并比对排序统计量可以发现,这一标准差的主要来源是少量极端性情况,即在大部分人成绩中等的同时,有小部分学生取得了优秀和不及格的成绩,从而使整体的标准差增大。
[1]万玉凤,柴葳.中国高等教育将真正走向世界——我国工程教育正式加入《华盛顿协议》的背后[N].中国教育报,2016-6-3.
[2]中国工程教育专业认证协会秘书处.工程教育认证工作指南(2016版)[Z].2015.
[3]陈宗荣.基于雷达图的学生学业水平评价技术[J].中国教育信息化,2015(22):76-78.
[4]刘汝倩,佘冰,朱欣焰,呙维.社会经济重心轨迹的语义方向玫瑰图生成方法及应用[J].计算机应用研究,2015 (12):3582-3585.
(编辑:王天鹏)(编辑:王晓明)
G40-058.1
A
1673-8454(2017)05-0065-03
湖南省普通高等学校教学改革研究项目 “面向MOOC的 《数字图像处理》可视化编程远程实验系统研究”(521293198);湖南大学教学改革研究项目“面向MOOC的《科学与工程计算方法及应用》远程实验系统研究”(521202085);教育部卓越工程师计划项目:湖南大学测控技术与仪器(教高[2011]1号);全国专业改革综合试点项目:湖南大学测控技术与仪器专业综合改革(教高司函[2011]226号)。
