多维关联函数建模及其低碳实例检索应用

2017-04-07洪欢欢赵燕伟陈尉刚

中国机械工程 2017年6期

关键词：空气压缩机螺杆实例

洪欢欢赵燕伟陈尉刚

1.浙江工业大学特种设备制造与先进加工技术教育部/浙江省重点实验室，杭州，3100142.宁波大学高等技术研究院，宁波，315211

多维关联函数建模及其低碳实例检索应用

洪欢欢1,2赵燕伟1陈尉刚1

1.浙江工业大学特种设备制造与先进加工技术教育部/浙江省重点实验室，杭州，3100142.宁波大学高等技术研究院，宁波，315211

针对低碳设计多维度实例检索建模及其降维计算问题，提出了一种多维关联函数建模及其检索应用方法。首先，通过变斜率原理改进侧距，构建了基于改进侧距的多维侧距模型。然后，针对侧距难以准确描述设计参数与最优值之间距离的问题，建立了多维关联函数及其三层次的低碳实例检索方法。最后以螺杆空压机为例进行了验证，结果表明了改进侧距的正确性和有效性、多维关联函数降维计算的快速性与有效性，以及低碳实例检索的合理性与实例间的差异性。

多维关联函数；低碳实例；相似检索；空间降维；螺杆空气压缩机

0 引言

低碳实例检索是产品低碳设计的关键步骤，且在产品设计活动中，大约75%的设计是基于实例的产品设计[1]。因此相似产品实例的相似性计算方法决定了检索的质量和可靠性[2]，从而影响基于实例的产品低碳设计效果。目前，相似度检索的研究主要集中在相似度建模与相似算法上。相似度建模的研究方法众多[3]，最常用的是基于K临近算法[4-6]、归纳索引法[7]和知识导引法。这些方法比较适合定性问题的检索，对模糊或定量问题的实例检索就无能为力。基于可拓理论[8-9]、基于图论[10]、子空间法[11]和神经网络[12]等的检索方法，主要计算单一属性相似度并集成求解全属性的相似度，而多维不同量纲低碳需求的相似度计算结果，可能并不是通过各个单维属性相似度取大、取小或加权求和等方法获得的。

多维空间检索技术分为空间索引技术和降维技术，前者包含2类索引方法[13]，其共同点是对空间进行分割来缩小空间求解维度；后者有主成分分析法[14]和语义索引等，这些方法的特点是对空间进行有效降维，将高维数据降至低维以简化计算，但缩减的空间或低维空间并不一定是在熟知的三维空间内，导致降维的有效性不能保证。

本文研究面向低碳实例单属性检索的侧距改进、多属性检索的多维关联函数建模及其在实例库中的具体应用。

1 面向低碳实例单属性检索的侧距改进

侧距[15]描述区间内的点到该区间的距离关系，其值不全为0，而且文献[15]中构建的侧距模型曲线是等斜率变化的。这不同于经典距描述的区间内的点到该点所在区间的距离都为0。侧距可分为左右侧距，区分的方式是判断区间最优值点是在该区间中点的左侧或右侧。机械设计应用中，设计参数的选取往往不在参数区间的中点，所以，侧距存在一定的局限性。文献[16]针对区间最优值为区间中点的特殊情况做了改进研究，使得侧距在检索中具有较好的应用效果。

低碳实例是指包含全生命周期各个阶段的碳足迹、成本、性能、结构等全面信息的产品实例。低碳需求最优值并非在需求区间的中点，并且现有的侧距计算结果无法有效区分设定相同最优值位置条件下区间内各点的实际设计意义[17]。以普通左侧距(图1中的双点划线)计算为例，在最优值x0下，区间内点x3、x2(x2-x0=x0-x3)的侧距有ρ(x2)>ρ(x3)，这就与机械设计实际意义产生了冲突。因此，对等斜率的侧距进行变斜率改进，并基于二次曲线进行变斜率数学建模，构建改进的左侧距模型。图1表示了4种状态的左侧距：普通左侧距(双点划线)、特殊侧距(单点划线)、改进左侧距(加粗虚线)、特例改进距(细虚线)。

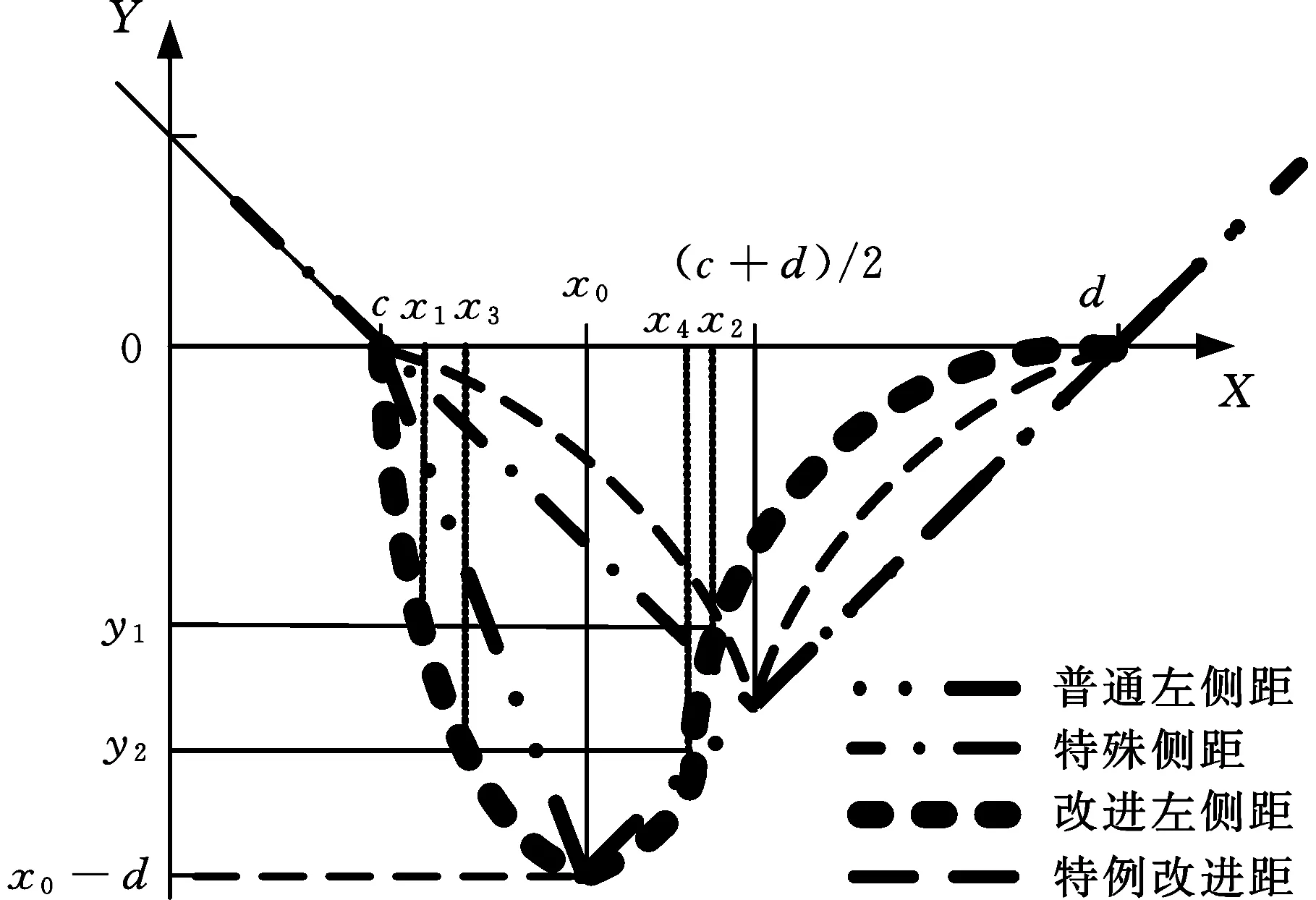
图1 改进左侧距对比效果Fig.1 Contrast effect of improved left side distance

当c≤x0≤(c+d)/2时，改进后的左侧距公式为

(1)

2 面向低碳实例空间检索的多维关联函数构建

2.1 基于改进侧距的多维侧距构建

如图2所示，由侧距本质[18]与图1中的侧距平面化转换表示方式可知，一维侧距可视为求解点x到区间两端点的位置距离，二维侧距可视为点P到过最优点O的直线与一维线段交点(P1、P2)的距离，三维侧距可视为点P到过最优点O的直线与二维平面交点(P1、P2)的距离，以此类推，n维空间侧距可视为最优点到过最优点的直线与n-1维空间体的交点的距离。n维侧距的交点公式为

式中，ai为由平面方程求解而得的常数；xi表示实例库中实例P的第i个属性。

过n维空间点P(x11，x12，…，x1n)、最优x0(x01，x02，…，x0n)的直线的方程为

现以三维侧距(图2c)建模为例，设属性点P落于锥体OA′B′C′D′中，过最优点O和点P的直线lop与边框交点为P1和P2。三维右侧距模型距离函数：

(6)

其中，e为空间点(1,1,…,1)；S1为一个实际产品需求的多维空间；F3(S1)表示1个三维点中的每个需求维度区间向其他二维需求空间垂直映射所构成的封闭多维空间的边界，当点P中的每个维度数值相等时，所构成的边界是一样的，反之亦然；O≠F3(S1)表示空间最优点不在边界面上；P1为三维空间中的点O与P所在直线和F3(S1)的交点；d(P,P1)为点P与点P1的线性距离；[O，P2]为直线lx0P上点O与点P2所构成的点区间；P∈[O,P2]表示点P在直线lx0P上，极限位置是O与P2。

由式(5)、式(6)可知，一维侧距、二维侧距、三维侧距都可由空间属性点之间的距离公式表示，可见n维侧距也是计算空间属性点的距离问题。多维侧距可以解决单维侧距集成加权运算过程中的主观化权重赋值问题，实现多维侧距的客观化求解。显然，多维侧距推导过程涉及较多的计算步骤，且公式选取的判断条件相对繁琐，当维数较高时，无法直接计算距离。

2.2 基于多维侧距的多维关联函数

多维关联函数是多个多维侧距的集成运算公式，具有简化空间距离计算等优势。假设低碳需求区间Hi=[xi,j1,xi,j2]且xi,j1≤xi,j2，则经典域空间S1=((Δx1,1, Δx1,2, … , Δx1,m), 0)，Δxi,j=xi,j2-xi,j1。低碳多维属性作为可拓域空间S2=((Δx1′,1,Δx1′,2, … ,Δx1′,m), 0)，可知S2是基于S1的扩大空间，满足S2⊃S1。对于趋大型产品，Si,2=[xi,j1, 2xi,j0-xi,j1]，Si,2为第i个维度的需求可拓域空间，xi,j0为该维度属性的需求最优值。对于趋小型产品，2xi,j0-xi,j2≥0时，Si,2=[2xi,j0-xi,j2,xi,j2]； 2xi,j0-xi,j2<0时，取xi,i0=d/2，Si,2=[0,xi,j2]。结合文献[18]中的一维关联函数可得多维关联函数公式：

(7)

其中，R是指实域集。

3 基于多维关联函数的低碳实例相似检索

针对低碳实例的多属性需求相似检索问题，构建多级检索机制，原理如图3所示。将低碳与成本需求作为一级检索对象，输出至少有一种需求满足的低碳实例(以此作为二级检索的实例源)。这样做是为了减少不必要的数据计算、无效结果的输出，凸显低碳设计的重要性。之后，输入产品性能需求，做多维数据的二级检索。计算基于多维关联函数的相似度(式(7))，把实例源划分为产品性能需求全满足和产品性能需求不全满足这两个实例域。最后，输入多维产品零部件需求，再次划分上层的低碳实例域，输出产品零部件需求匹配的产品实例集。

第一、二层级的相似度函数是基于多维关联函数构建的：

(8)

其中，Hi表示第i次需求；j表示第j层级，j=1，2；t表示实例库中第t个实例P,t=1,2,…,N；N为实例总数。

第三级检索相似度：

(9)

其中，m1、m2分别为第一级与第二级检索的总属性维度。

基于多维关联函数的相似度检索算法构建步骤如下：

(1)判定产品需求类型，确定产品需求参数(可以是一个值，也可以是一个区间)；

(2)依据产品需求区间值构建多维经典域空间S1和多维可拓域空间S2；

(3)结合产品实例属性点Pt和最优点x0，构建直线lOP和n维空间；

(4)依据点Pt求解方程，给出Pt所属区域；

(5)计算Kn(Pt)；

(6)依据式(7)，判断Kn(Pt)与0的大小，依据式(8)、式(9)，计算各级相似度；

(8)结束。

低碳需求与低碳实例总的相似度包含了3个级别检索的相似度，不同检索级别权重设定为w1=0.5，w2=0.3，w3=0.2。所以低碳产品需求与低碳实例相似度公式：

(10)

4 实例应用

4.1 基于螺杆空气压缩机实例的改进侧距验证

选取不同品牌、不同系列的37 kW大型螺杆空气压缩机的17个低碳实例(表1)进行验证分析——以第i次低碳需求输入求解为例。

4.2 基于螺杆空气压缩机实例库的多维关联函数降维效果验证

选取排气压力、排气量、噪声、购买成本、产品上市碳足迹与使用碳足迹这6个指标需求，检索表1的螺杆空气压缩机实例库，以KHE37螺杆空气压缩机相似检索为例。

(1)依据改进侧距计算6个需求，判定Hi,4、Hi,ni-1和Hi,ni这三个需求不满足，即该型号螺杆空气压缩机特征有效维度为3，因此，可构成一个三维空间(每个特征为一个维度)。

表1 第i次低碳需求及部分螺杆空气压缩机实例的部分参数

(3)计算多维关联函数及确定点P的位置，得K3(P)=-|P1P|=-0.042，且空间点P所在区域位置对应的产品特征轴是Hi,ni-1。

(4)计算空间点P所在位置对应的一维关联函数。Hi,ni-1对应的经典域为S1,i,ni-1、可拓域为S2,i,ni-1、最优值为x0,i,ni-1时，计算得到K1(P) =-0.042。

(5)判断K3(P)、K1(P)的大小，得到K3(P)=K1(P)。

在该需求下，KHE37螺杆机实例检索的六维空间计算可等价降维到一维关联函数的计算，即多维属性计算可以等价为某一维度参数计算，说明降维效果明显。其他实例的计算过程不再赘述。

4.3 基于多维关联函数的低碳产品实例相似检索应用

现以表1所示的所有型号螺杆空气压缩机实例库多级检索为例，确定低碳需求中Hi,4、Hi,n-1和Hi,n这三个特征为一级检索特征。依据这3个需求特征区间及特征参数期望，确定其所对应的最优值，结合正态分布计算得到最优值x0,i,4=45 800，x0,i,n-1=148 361.5，x0,i,n=18 895.7；构成可拓域空间的各个特征参数子空间S1,i,4=[28 600，63 000]，S1,i,n-1=[136 723，160 000]，S1,i,n=[13 791.4，24 000]。

Hi,1、Hi,2和Hi,3为二级检索特征，对应的最优值x0,i,1=1.1，x0,i,2=5.2，x0,i,4=69；构成可拓域空间的各个特征参数子空间S1,i,1=[0.9，1.3]，S1,i,2=[3.8，6.4]，S1,i,n=[51，70]。

在三级检索过程中，由于Hi没有第三类检索的需求特征，因此，该阶段各个螺杆空气压缩机实例特征的有效维度、多维关联函数值分别默认为0和1。

应用螺杆机低碳需求及与螺杆空气压缩机实例相似度计算公式，综合计算各个阶段的相似度与总的需求和实例相似度。以螺杆空气压缩机KHE37为例说明相似度计算：①产品属性点Pt

表2 基于部分螺杆空气压缩机实例的相似检索结果

中的t=17；②一级检索的螺杆空气压缩机需求与实例相似度s1(Hi,P17)=1；③二级检索的螺杆空气压缩机需求与实例相似度s2(Hi,P17)=1；④三级检索的螺杆空气压缩机需求与实例相似度s3,i,17(Hi,P17)=1；⑤总的相似度si,17(Hi,P17)=1。

5 结语

本文针对区间内侧距计算公式无法有效区分设计参数相对于设计参数最优值的变化问题，通过变斜率方式改进等斜率的侧距，建立了改进侧距公式。针对螺杆空气压缩机低碳需求的多维性，并为消除单一维度加权计算时权重赋值主观化的影响，构建了基于多维侧距的多维关联函数。当n维空间的中心与螺杆空气压缩机特征参数最优值相同时，多维关联函数具有良好的降维性。当n维设计需求空间的中心与螺杆空气压缩机实例特征参数最优值相同时，多维关联函数具有良好的降维性。

为克服基于一维关联函数的相似度方法具有较强主观性的问题，建立了基于三级检索机制的模型，给出了基于多维关联函数的相似度检索算法步骤，并对由螺杆空气压缩机实例组成的产品实例库进行低碳属性检索，验证了该方法的可行性，讨论了不同相似度下各个螺杆空气压缩机实例满足低碳需求的难易程度。

[1] 蒋炳炎, 沈龙江, 彭华健. 微注射成形中变模温控制技术[J]. 中国塑料, 2006, 20(3): 99-102.JIANGBingyan,SHENLongjiang,PENGHuajian.CurrentSituationandProspectofDynamicMoldTemperatureControlinMicroInjectionMolding[J].ChinaPlastic, 2006, 20(3): 99-102.

[2] 付相君，李善平. 产品的相似性推理：一种描述逻辑的方法[J]. 计算机辅助设计与图形学学报, 2006, 18(4)：569-573.FUXiangjun,LIShanping.ProductSimilarityReasoning:aDescriptionLogicApproach[J].JournalofComputer-AidedDesign&ComputerGraphics, 2006, 18(4)：569-573.

[3]YURIA，ANDRZEJK.SimilarityConceptforCase-basedDesigninProcessEngineering[J].ComputersandChemicalEngineering，2006，30：548-557.

[4]CHIEHYT，CHUANGCC.ACase-basedReasoningSystemforPCBPrincipalProcessParameterIdentification[J].ExpertSystemswithApplication，2007，32：1183-1193.

[5] 蒋占四，陈立平，罗年猛. 最近邻实例检索相似度分析[J]. 计算机集成制造系统，2007，13(6)：1165-1168.JIANGZhansi,CHENLiping,LUONianmeng.SimilarityAnalysisinNearest-neighborCaseRetrieval[J].ComputerIntegratedManufacturingSystems, 2007，13(6)：1165-1168.

[6] 周凯波，冯珊，李锋. 基于案例属性特征的相似度计算模型研究[J]. 武汉理工大学学报(信息与管理工程版)，2003，25(1)：24-27.ZHOUKaibo,FENGShan,LIFeng.ResearchoftheSimilarityCalculationModelsBasedontheFeaturesofCase[J].JournalofWuhanUniversityofTechnology(Information&ManagementEngineering), 2003，25(1)：24-27.

[7] 凌海风, 郭坚毅, 严骏, 等. 案例推理技术用于故障诊断时的相似算法[J]. 解放军理工学报(自然科学版), 2006, 7(5): 480-484.LINGHaifeng,GUOJianyi,YANJun,etal.SimilarityAlgorithmofCBRTechnologyAppliedtoFaultDiagnosingField[J].JournalofPLAUniversityofScienceandTechnology(NaturalScienceEdition), 2006, 7(5): 480-484.

[8] 赵燕伟, 苏楠, 张峰, 等. 基于可拓实例推理的产品族配置设计[J]. 机械工程学报, 2010, 46(15):146-154.ZHAOYanwei,SUNan,ZHANGFeng,etal.ConfigurationDesignMethodforProductFamilyBasedonExtensionCaseReasoning[J].JournalofMechanicalEngineering, 2010, 46(15): 146-154.

[9] 贾艳华, 莫容, 杨海成, 等. 基于可拓理论的CBR系统实例检索模型[J]. 计算机工程与应用, 2013, 49(2): 258-260.JIAYanhua,MORong,YANGHaicheng,etal.ModelforCaseRetrievalinCBRSystemBasedonExtenics[J].ComputerEngineeringandApplications, 2013, 49(2): 258-260.

[10] 胡伟, 胡国清, 魏昕, 等. 基于图论的产品实例检索结构相似度分析[J]. 农业机械学报, 2011, 42(8): 184-189.HUWei,HUGuoqing,WEIXin,etal.StructuralSimilarityAnalysisinCaseRetrievalUsingGraphTheory[J].TransactionsoftheChineseSocietyforAgriculturalMachinery, 2011, 42(8): 184-189.

[11] 钟诗胜, 王体春, 王威. 基于子空间法的多级实例分类检索与匹配模型[J]. 中国机械工程, 2009, 20(7): 767-772.ZHONGShisheng,WANGTichun,WANGWei.ClassRetrievalandMatchingModelofMulti-hierarchyCaseBasedonSubspaceMethod[J].ChinaMechanicalEngineering, 2009, 20(7): 767-772.

[12] 毛权, 肖人彬, 周济.CBR中基于实例特征的相似实例检索模型研究[J]. 计算机研究与发展, 1997, 34(4): 257-264.MAOQuan,XIAORenbin,ZHOUJi.ResearchonCase-feature-basedCaseIndexingModelsinCBR[J].ComputerResearch&Development, 1997, 34(4): 257-264.

[13]KIMC,HAH,LEEJH,etal.HerbalExtractPreventsBoneLossinOvariectomizedRats[J].ArchivesofPharmacalResearch, 2003, 26: 917- 924.

[14] 张秀芬, 张树有, 伊国栋. 产品多粒度层次可拆卸性评价模型与方法[J]. 浙江大学学报(工学版), 2010, 44(3): 581-588.ZHANGXiufen,ZHANGShuyou,YIGuodong.Multi-granularityandHierarchyDisassemblabilityEvaluationModelandMethodologyforProducts[J].JournalofZhejiangUniversity(EngineeringScience), 2010, 44(3): 581-588.

[15] 杨春燕, 蔡文. 可拓学：理论、方法与应用[M]. 北京：科学出版社, 2013.YANGChuanyan,CAIWen.Extenics:Theory,MethodandApplication[M].Beijing:SciencePress, 2013.

[16]ZHAOYanwei,WANGHuan,HONGHuanhuan.Cased-basedReasoningBasedonExtensionTheoryforConflictResolutioninCooperativeDesign[C]//9thInternationalConferenceonCooperativeDesign,Visualization,andEngineering.Osaka, 2012: 134-142.

[17] 杨春燕, 李小妹, 陈文伟, 等. 可拓数据挖掘方法及其计算机实现[M]. 广州: 广东高等教育出版社, 2010.YANGChuanyan,LIXiaomei,CHENWenwei,etal.ExtensionDataMiningMethodandItsComputerImplementation[M].Guangzhou：GuangdongHigherEducationPress, 2010.

[18] 杨春燕, 蔡文. 可拓工程[M]. 北京: 科学出版社, 2010.YANGChuanyan,CAIWen.ExtensionEngineering[M].Beijing:SciencePress, 2010.

(编辑张洋)

Modeling of Multi-dimensional Correlation Function and Its Applications for Low Carbon Case Retrieval

HONG Huanhuan1,2ZHAO Yanwei1CHEN Weigang1

1.Key Lab of E&M，Ministry of Education & Zhejiang Province，Zhejiang University of Technology，Hangzhou，310014 2.The Research Institute of Advanced Technologies,Ningbo University Nigbo,Zhejiang,315211

To solve problems of multidimensional case retrieval modeling and its dimensionality reduction calculation for low carbon design, a modeling and application method of multi-dimensional correlation function was proposed. Firstly, an improved side distance method was developed through the principles of variable slope, which provided the basis for developing a multi-dimensional side distance model. Secondly, because side distance formula could not give out the accurate distance values between design parameters and its optimal, a multi-dimensional correlation function which had good dimension reduction effect was established. Then a retrieval method was given based on the multi-dimensional correlation function. Finally, the proposed method and algorithms were verified in the design of a screw air compressor. The evaluation results show that the improved side distance is correct and effective, the dimension reduction method for the multi-dimensional correlation function is fast and viable, and the otherness among these cases is very obvious.

multi-dimensional correlation function; low-carbon case; similarity retrieval; dimension reduction; screw air compressor

2015-01-09

国家自然科学基金资助项目(51605231，51275477)

TP18DOI：10.3969/j.issn.1004-132X.2017.06.009

洪欢欢，男，1984年生。浙江工业大学机械工程学院博士研究生，宁波大学高等技术研究院讲师。主要研究方向为低碳设计、创新设计、技术成果转化。发表论文10余篇。赵燕伟(通信作者)，女，1959年生。浙江工业大学机械工程学院教授、博士研究生导师。E-mail:zyw@zjut.edu.cn。陈尉刚，男，1989年生。浙江工业大学机械工程学院硕士研究生。