Euler方程φ(xy)=k1φ(x)+k2φ(y)(k1≠k2)的正整数解
2017-04-07张四保官春梅席小忠
张四保, 官春梅, 席小忠
(1.喀什大学 数学与统计学院 新疆 喀什 844008; 2.宜春学院 数学与计算机科学学院 江西 宜春 336000)
Euler方程φ(xy)=k1φ(x)+k2φ(y)(k1≠k2)的正整数解
张四保1, 官春梅1, 席小忠2
(1.喀什大学 数学与统计学院 新疆 喀什 844008; 2.宜春学院 数学与计算机科学学院 江西 宜春 336000)
讨论了一个形如φ(xy)=k1φ(x)+k2φ(y)(k1≠k2)的具体方程φ(xy)=5φ(x)+7φ(y)的可解性,给出了其一切整数解.并根据这一方程的解的情况,给出了(x,y)=(k1+k2,k1+k2)是方程φ(xy)=k1φ(x)+k2φ(y)(k1≠k2)的1组整数解的结论,这里的k1,k2都是正整数.
Euler函数; 可解性; 整数解
0 引言
方程整数解的研究是数论研究中的一个重要课题之一,其研究内容与成果也很丰富[1-3],令φ(n)为Euler函数是数论研究中的一个重要函数.关于包含Euler函数φ(n)的方程的研究有着丰富的研究成果[4-9].对于形如
φ(xy)=k1φ(x)+k2φ(y),(k1,k2是正整数)
(1)
的讨论,大多文献讨论的都是当k1=k2的情况,即讨论的是形如φ(xy)=k(φ(x)+φ(y))的方程.文献[10]研究了当k为素数时,方程φ(xy)=k(φ(x)+φ(y))的正整数解,并给出了当k=3时其所对应方程的部分正整数解.文献[11]研究了方程φ(xy)=3(φ(x)+φ(y))的可解性,并给出其全部的35组正整数解.文献[12]研究了方程φ(xy)=7(φ(x)+φ(y))的可解性,并给出了其全部的15组正整数解.本文将讨论形如方程(1)的具体方程的一切整数解问题.并根据这一具体方程解的情况,给出了方程(1)中有(x,y)=(k1+k2,k1+k2)解的结论.
φ(xy)=5φ(x)+7φ(y)
(2)
1 引理
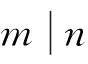
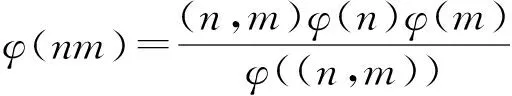
引理3[13]当n≥3是整数,则φ(n)为偶数.
引理4[14]方程φ(x)=14无正整数解.
2 定理及其证明
定理1 方程(2)有整数解(x,y)=(43, 7),(43, 9),(43, 14),(43, 18),(49, 9),(49, 18),(86, 7),(86, 9),(98, 9),(13, 21),(13, 28),(13, 36),(13, 42),(21, 13),(21, 26),(26, 21),(28, 13),(36, 13),(42, 13),(15, 41),(15, 82),(15, 88),(16, 41),(16, 55),(16, 75),(20, 41),(24, 41),(24, 55),(30, 41),(14, 18),(18, 14),(8, 50),(8, 66),(10, 44),(10, 66),(12,50),(15, 24),(24, 15),(12, 44),(12, 12).
证明 对于方程(1),设gcd(x,y)=d,则由引理1可知,存在x1,y1∈Z+,使得φ(x)=x1φ(d),φ(y)=y1φ(d). 再由引理2,有φ(xy)=x1y1dφ(d).结合方程(1),有d=k1y1-1+k2x1-1.由于k1≠k2,不妨设k1 在方程(2)中,k1=5,k2=7.因而,只需考虑gcd(x,y)=d∈[1,14]的情况. 当x1=42,y1=6时,有φ(x)=x1φ(d)=42,φ(y)=y1φ(d)=6.因而有x=43,49,86,98,y=7,9,14,18. 因而,此时方程(2)有整数解(x,y)=(43, 7),(43, 9),(43, 14),(43, 18),(49, 9),(49, 18),(86, 7),(86, 9),(98, 9). 当x1=14,y1=10时,有φ(x)=x1φ(d)=14,φ(y)=y1φ(d)=10.由引理4可知,方程(2)无整数解. 当x1=y1=12时,有φ(x)=x1φ(d)=12,则x=y=13,21,26,28,36,42.方程(2)有整数解(x,y)=(13, 21),(13, 28),(13, 36),(13, 42),(21, 13),(21, 26),(26, 21),(28, 13),(36, 13),(42, 13). 当x1=8,y1=40时,有φ(x)=x1φ(d)=8,φ(y)=y1φ(d)=40.因而有x=15,16,20,24,30,y=41,55,75,82,88, 100,110,132,150. 因而,此时方程(2)有整数解(x,y)=(15, 41),(15, 82),(15, 88),(16, 41),(16, 55),(16, 75),(20, 41),(24, 41),(24, 55),(30, 41). 当x1=21,y1=3时,有φ(x)=x1φ(d)=21,φ(y)=y1φ(d)=3.由引理3可知,此时方程(2)无整数解.同理,当x1=7,y1=5时,方程(2)亦无整数解. 当x1=y1=6时,φ(x)=φ(y)=6,有x=y=7,9,14,18.方程(2)有整数解(x,y)=(14, 18),(18,14). 当x1=4,y1=20时,有φ(x)=x1φ(d)=4,φ(y)=y1φ(d)=20.因而有x=5,8,10,12,y=25,33,44,50,66.因而,此时方程(2)有整数解(x,y)= (8, 50),(8, 66),(10, 44),(10, 66),(12, 50). 当x1=14,y1=2时,有φ(x)=x1φ(d)=28,φ(y)=y1φ(d)=4.因而有x=29,58,y=5,8,10,12. 由于,以上x,y的值没有满足gcd(x,y)=3. 因而,此时方程(2)无整数解. 当x1=4,y1=4时,有φ(x)=x1φ(d)=y1φ(d)=8.因而有x=y=15,16,20,24,30. 因而,此时方程(2)有整数解(x,y)=(15, 24),(24, 15). 当x1=3,y1=3时,有φ(x)=x1φ(d)=y1φ(d)=6.因而有x=y=7,9,14,18. 由于以上x,y的值没有满足gcd(x,y)=3. 因而,此时方程(2)无整数解. 当x1=2,y1=10时,有φ(x)=x1φ(d)=4,φ(y)=y1φ(d)=20.因而有x=5,8,10,12,y=25,33,44,50,66. 因而,此时方程(2)有整数解(x,y)=(12, 44). 当x1=7,y1=1时,有φ(x)=x1φ(d)=14,φ(y)=y1φ(d)=2.由引理4可知,此时方程(2)无整数解. 当x1=2,y1=2时,有φ(x)=x1φ(d)=y1φ(d)=4.因而有x=y=5,8,10,12.方程(2)无整数解. 综合以上讨论,可得本文结论. 证毕. 在定理1中,当k1=5,k2=7时,方程(2)有解,(x,y)=(12,12),此时k1+k2=12.那么,对于任意的正整数k1,k2,方程(1)是否一定有(k1+k2,k1+k2)这一组解.为此,证明了以下结论. 定理2 对于任意的正整数k1,k2,(x,y)=(k1+k2,k1+k2)是方程(1)的1组解. 本文讨论了当k1=5,k2=7时方程φ(xy)=5φ(x)+7φ(y)的解问题.而对于其他的正整数k1,k2,效仿定理1中方程的讨论,同样可以得到相对应方程的解,只不过当k1,k2中有一数略大时,需分2 max{k1,k2}种情况讨论. [1] 管训贵.关于Diophantine方程x3±1 = 2pqry2[J].郑州大学学报(理学版),2015,47(2):49-52. [2] 杜先存,管训贵,万飞.关于不定方程x3-1 = 3pqy2的整数解研究[J].郑州大学学报(理学版),2014,46(3):13-16. [3] 张四保.七元一次不定方程整数解解公式[J].郑州大学学报(理学版),2013,45(3):28-31. [4] 张利霞,赵西卿,郭瑞,等.关于数论函数方程S(SL(n))=φ(n)的可解性[J].纯粹数学与应用数学,2015,31(5):533-536. [5] 张四保,刘启宽.关于Euler函数一个方程的正整数解[J].东北师大学报(自然科学版),2015,47(3):49-54. [6] 刘艳艳.数论函数方程φ(n)=S(nk)的非平凡解[J].青岛科技大学学报(自然科学版),2014,35(3):326-329. [7] 张四保,杜先存.一个包含Euler函数方程的正整数解[J].华中师范大学学报(自然科学版),2015,49(4):497-501. [9] 热伊麦·阿卜杜力木. 与Euler函数φ(n)有关的几个方程[J].吉林师范大学学报(自然科学版),2015,36(4):71-75. [10] SUN C F,CHENG Z. Some kind of equations involving euler functionφ(n)[J].Journal of mathematical study,2010,43(4):364-369. [11] 张四保.有关Euler函数φ(n)的方程的正整数解[J].数学的实践与认识,2014,44(20):302-305. [12] 孙树东.一个与Euler函数φ(n)有关的方程的正整数解[J].北华大学学报(自然科学版),2015,16(2):161-164. [13] ROSEN K H. Elementary number theory and its applications[M].Pittsburgh:Academic wesley,2005. [14] 姜友谊.关于Euler函数方程φ(x)=m的解[J].重庆工业管理学院学报,1998,12(5): 91-94. (责任编辑:方惠敏) The Integer Solutions of Euler Equationφ(xy)=k1φ(x)+k2φ(y)(k1≠k2) ZHANG Sibao1, GUAN Chunmei1, XI Xiaozhong2 (1.SchoolofMathematicsandStatistics,KashgarUniversity,Kashgar844008,China;2.InstituteofMathematicsandComputerScience,YichunCollege,Yichun336000,China) The solvability of a specific equationφ(xy)=5φ(x)+7φ(y),such asφ(xy)=k1φ(x)+k2φ(y),was discussed.And all integer solutions were given. According to the condition of its solutions, a conclusion that (x,y) = (k1+k2,k1+k2) was a positive integer solution of equationφ(xy)=k1φ(x)+k2φ(y) was given, wherek1≠k2, andk1,k2were positived integers. Euler function; solvability; integer solution 2016-08-11 国家自然科学基金项目(11201411);喀什大学校内项目(142513). 张四保(1978—),男,江西峡江人,副教授,主要从事数论研究,E-mail:sibao98@sina.com. O156 A 1671-6841(2017)01-0007-04 10.13705/j.issn.1671-6841.2016200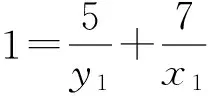
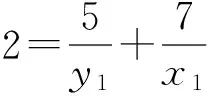
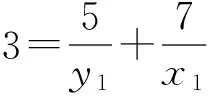
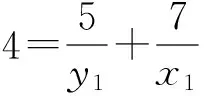
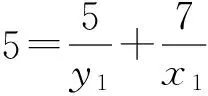
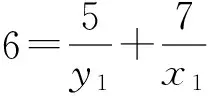
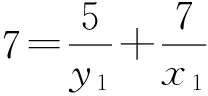
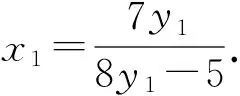
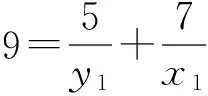
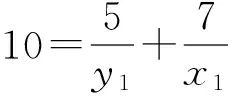
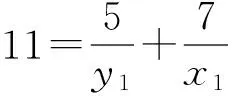
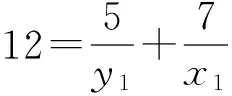
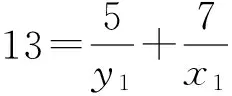
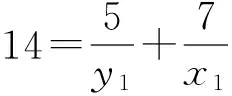
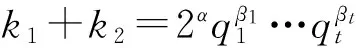
3 结语
