一种优化齿槽转矩抑制永磁同步电机振动和噪声的方法

王明星, 王爱元, 李轶华

(上海电机学院， 上海 201306)

一种优化齿槽转矩抑制永磁同步电机振动和噪声的方法

王明星, 王爱元, 李轶华

(上海电机学院， 上海 201306)

合理控制齿槽转矩可以降低电机的振动和噪声。为了降低永磁同步电机的振动和噪声，对影响齿槽转矩的四个主要参量(极弧系数、偏心距、气隙长度、磁极厚度)进行优化，然后利用有限元分析软件，进行电机的振动和噪声的分析。首先利用正交试验选取一定数量的样本；然后利用支持向量机对其进行拟合，得到回归方程；利用微粒群优化算法对其回归方程进行寻优，得到理想的齿槽转矩；最后将齿槽转矩带入电机模型中进行电机的振动和噪声的分析。

齿槽转矩； 振动和噪声； 正交试验； 支持向量机； 微粒群优化算法

0 引 言

电机的振动和噪声是一个重要课题[1]。电机被广泛应用于各个领域，其振动和噪声不仅能使其使用寿命下降，对人类身心健康也会造成一定影响。影响永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)振动和噪声的因素有很多，研究较多的是气隙径向电磁力[2]，而合理抑制齿槽转矩将会使齿谐波下降,也会对电机振动和噪声起到抑制作用。

PMSM空载时，永磁体与电机齿之间会产生作用力，其切向分力产生的电机转矩称之为齿槽转矩。齿槽转矩也是影响电机振动和噪声的一个因素，特别是在电机轻载或者低速运行时，齿槽转矩对PMSM振动和噪声的影响比较明显。在高性能PMSM的设计过程中，为了尽可能降低振动和噪声，可以合理的削弱齿槽转矩。在已有的研究中，已经分析了电机的极弧系数是影响齿槽转矩的一个重要因素[3]；另外也证明了随着磁体偏心距的增加，电机的齿槽转矩将会减小[4];此外电机的气隙长度也是影响齿槽转矩的重要因素[5];文献[6]证明了永磁体的厚度与齿槽转矩大小有重要关系。本文首先利用支持向量机(Support Vector Machine, SVM)算法建立需要寻优的目标方程[7-8]，然后利用微粒群优化算法(Particle Swarm Optimization, PSO)进行寻优，得到使齿槽转矩最小的四个参量的最佳取值，最后将取值导入电机模型中对PMSM进行振动和噪声分析。

1 PMSM振动和噪声分析过程

2010年，美国的Rakib Islam, Iqbal Husain学者研究并分析了PMSM的噪声和振动,研究表明，噪声和振动的根源是径向力引起的电磁振动而不是切向力引起的转矩脉动[9]。本文通过抑制PMSM的齿槽转矩进而有效地降低齿谐波，也会达到降低振动和噪声的效果。PMSM的振动和噪声求解都是通过有限元软件完成的，整个求解过程如图1所示。

图1 PMSM振动和噪声仿真计算流程

2 参数优化过程

2.1 初始齿槽转矩的计算

本文采用Ansys中的Maxwell软件对PMSM进行参数计算和分析过程。采用4极24槽的小功率PMSM作为研究对象，功率为 0.55kW，额定转速为 1500r/min，绕组采用单层 L 3 型接法，部分电机参数如表1所示。

表1 电机的初始参数

齿槽转矩是在PMSM空载时产生的，在模型建立好之后应给予零电流激励，且设置转速为1°/s。图2为表1中参数生成的齿槽转矩图，其最大值约为0.533N·m。

图2 初始齿槽转矩曲线

2.2 样本空间的建立

此步的建立就是为后续建模提供输入输出数据。本文中输入为四个设计变量，分别为极弧系数、偏心距、永磁体厚度、气隙长度,目标函数为电机齿槽转矩。其中每个设计变量取5个值，共有625个数据。为了简化试验，利用正交试验法选取建模需要的样本数据。

正交试验是用于多因素试验的一种方法，其是从全面试验中挑选出部分有代表性的数据进行试验，这些数据具有整齐和均匀的特点。正交试验是部分因子设计的主要方法，具有较高的效率和广泛的应用。试验中四个因素取值范围分别为： 极弧系数0.63～0.75，偏心距1～5mm，气隙长度0.5～1.2mm，磁极厚度1.5～3.5mm。试验中各因素选取的水平如表2所示，根据因素和水平的个数选取L25(56)的正交试验表，将25组数据带入到有限元软件中求解，得到SVM算法所需要的样本空间。

表2 因素水平表

2.3 支持向量回归机

智慧教室以学习者为中心，打破物理空间的束缚，为学习者打造一个开放的学习空间。其不再是一间封闭的教室。网络互联扩延了传统教室的空间，基于网络的互动教学突破了空间局限，调动了生生之间、师生之间、班级之间的互动积极性，让区域间的班级互动成为可能，学习也由个体的机械记忆转变为集体的、互动的过程。

SVM是一种针对有限数据模式识别问题进行研究的新型机器学习方法，主要有两大应用： 数据分类和回归拟合。SVM中为了降低维数运算及解决非线性问题，引进了核函数，常用的核函数主要有多项式核函数、高斯径向基核函数、线性核函数、多层感知机核函数和指数径向基核函数等。本文主要利用其回归拟合功能，选取高斯径向基核函数对数据样本进行分析求解。SVM中除了需要选择核函数，其内容还包括误差容量的选择、惩罚因数c的选择和γ参数的选择等。

2.4 建立SVM数学模型

本文采用SVM回归拟合功能,其方程为

(1)

b*——偏置参数。

从式(1)可看出，欲想得到回归方程，需要求取核函数的系数、25个支持向量、γ参数和偏置参数b*。利用libsvm工具箱对数据进行训练和测试，通过交叉验证的方法[10],求取最佳的惩罚参数c和核函数参数g(其中c为对误差的容忍度,即错分程度;g为γ参数)。

经过多次程序调试最终得到问题中的c=327，g=1.2。将model中的数据对应带入到式(1)中可以求出PSO寻优的目标函数式，SVM模型预测数据和真实数据之间的对比如图3所示。预测值与真实值基本一致，SVM回归模型有效。

图3 真实数据和拟合数据曲线

2.5 PSO算法寻优

PSO是由J.Kennedy和R.C.Eberhart于1995年提出的一种新的进化计算算法，其来源于鸟类或鱼类觅食过程中迁徙和群集的模拟[11]。在粒子群算法中,鸟与食物之间的距离由适应度函数体现出来,一个微粒代表一只鸟,当鸟觅食完毕,就代表微粒通过改变自身空间位置使适应度函数取得了潜在最优解。每个微粒都具有速度、位置和自身适应值三个特征，位置和速度是寻优过程中的两个主要参数，其中个体位置在个体极值和群体极值中完成更新；速度则决定了搜索的方向和范围，速度值设置不当，容易使试验陷入局部最优化。

假设在一个D维搜索空间中，有m个微粒组成一微粒群，其中第i个微粒的空间位置为xi=(xi1,xi2,xi3,…,xid),其为优化问题的一个潜在解，将其代入目标函数中可以计算出相应的适应值，据适应值的大小可衡量xi的优劣；第i个微粒所经历的最好位置记为Pi=(Pi1,Pi2,Pi3,…,Pid)，每个微粒还具有各自的飞行速度vi=(vi1,vi2,vi3,…,vid),在微粒群中，所有微粒经历过的最好位置记为Pg=(Pg1,Pg2,Pg3,…,Pgd)。根据J.Kennedy和R.C.Eberhart最早提出的PSO，对每一代微粒，其迭代后的位置和速度公式分别为

(2)

(3)

式中：ω——惯性权值；c1、c2——正的常数，称为加速系数；r1、r2——2个在[0,1]范围内变化的随机数。

对于本文研究的优化问题,将四个设计变量的取值范围作为约束条件,(x1,x2,x3,x4)作为一个微粒的坐标,回归方程作为其适应度函数。利用微粒群算法对其进行优化,进化次数为 1000,种群规模为200,为了防止其陷入局部最优化,设置其vmax=10000，vmin=-10000。另外为了防止早熟收敛及后期迭代效率不高等缺点，引入了简单变异算子。经PSO寻优后，得到最优值为0.1959N·m，所对应的变量取值为(0.719,4.945,0.903,2.031),PSO寻优曲线如图4所示。

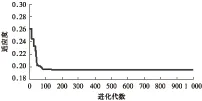
图4 PSO寻优曲线

将优化后的结果带到有限元分析软件中，仿真出的齿槽转矩如图5所示。从图5中可看出优化后齿槽转矩最大值为0.164N·m，与算法优化的结果相差不大，与图2中的0.533N·m相比减少很多,说明研究是有意义的，同时仿真结果也验证了算法的准确性。

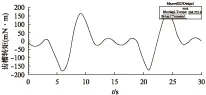
图5 优化后的齿槽转矩曲线

3 振动和噪声分析实例

从图8(a)、图8(b)中可看出经过优化后齿槽转矩产生的声压等级比初始时的声压等级要小，说明PMSM经过优化后其振动和噪声减小了。

图6 定子内表面径向和切向磁拉力

PMSM振动和噪声涉及到三个场的耦合[9],在Maxwell 2D中,利用该电机的全模型,计算定子内表面径向和切向磁拉力,如图6所示。将其作为激励源耦合到Ansys Mechanical中进行该电机三维定子谐响应分析,如图7所示。然后将谐响应分析结果作为激励源耦合到Ansys Mechanical ACT中进行三维声场分析,如图8所示。

图7 谐响应分析结果

图8 三维声场分析结果

降低齿槽转矩能够合理抑制振动和噪声。本文将初始齿槽转矩和优化后齿槽转矩产生的声压级(Sound Pressure Level, SPL)进行对比,从对比的结果中可以看出,优化后齿槽转矩的SPL比初始SPL效果要好,也说明了通过优化齿槽转矩来降低振动和噪声具有一定的研究意义。

4 结 语

本文从影响PMSM振动和噪声的因素出发,通过优化齿槽转矩进而有效抑制振动和噪声。在优化齿槽转矩的过程中,用SVM对其进行回归建模,在此基础上利用PSO算法对电机偏心距、磁体厚度、气隙长度及极弧系数进行优化，得到了一组使齿槽转矩最小的参数；然后将这两种不同参数的电机模型进行振动和噪声分析，通过对电磁场、谐响应、声场三者之间的耦合，最后得到两种不同的SPL；通过SPL的对比可以看出，经过优化后的电机SPL比之前降低了，说明研究具有一定的意义。

[1] 舒波夫.电机的噪声和振动[M].沈官秋,译，北京： 机械工业出版社，1980.

[2] JANG G H, LIEU D K. The effect of magnet geometry on electric motor vibration[J]. IEEE transactions on magnetics, 1991,27(6)： 5202-5204.

[3] 杨玉波，王秀和，丁婷婷，等.极弧系数组合优化的永磁电机齿槽转矩削弱方法[J].中国电机工程学报，2007，27(6)： 7-11．

[4] 秦虹.永磁无刷直流电动机齿槽转矩的削弱[J].电机技术，2009(12)： 10-13.

[5] 王广生，黄守道，高剑.基于Ansoft软件设计分析内置式永磁同步电动机[J].微电机，2011，44(2)： 70-73.

[6] 周俊杰，范承志，叶云岳.盘式永磁电机齿槽转矩的分析与抑制[J].机电工程，2009，26(2)： 79-81.

[7] 王群京，鞠鲁峰，钱喆，等.支持向量机理论及其在复杂电机设计中的应用[J].微特电机，2010(3)： 67-70.

[8] 彭春华，相龙阳，刘刚，等.基于支持向量机和微分进化算法的风电机优化运行[J].电网技术，2012，36(4)： 57-62.

[9] ISLAM R, HUSAIN I. Analytical model for predicting noise and vibration in permanent-magnet synchronous motors[J]. IEEE Transactions on Industry Applications,2010,46(6): 2346-2354.

[10] CAMPBELL C. Algorithmic approaches to training support vector machines： a survey[C]∥Proceedings of E-SANN2000. Bel-gium： D-Facto Publications，2000： 27-36.

[11] 范坚坚，吴建华，黎宪林，等.永磁同步电动机磁钢的多目标粒子群算法优化[J].电机与控制学报，2009，13(2)： 173-178.

A Way of Optimizing Cogging Torque to Reduce Vibration and Noise for Permanent Magnet Synchronous Motor

WANGMingxing,WANGAiyuan,LIYihua

(Shanghai Dianji University, Shanghai 201306, China)

The vibration and noise of motor could be reduced by keeping a reasonable control on cogging torque. To minimize the vibration and noise of PMSM, an optimization of four main parameters (pole-arc coefficient, eccentric distance, air-gap length and magnet thickness) that affect the cogging torque was done, combining with the finite element analysis method, to analyze the vibration and noise of PMSM. First of all, select a certain number of samples by using orthogonal experiments and fit them with SVM to get a regression equation, then, the ideal cogging torque could be obtained through the optimization of the equation. Finally, took the cogging torque into the motor model for the analysis of the vibration and noise of motor.

cogging torque; vibration and noise；orthogonal experiments；support vector machine(SVM)；particle swarm optimization(PSO)

王明星(1991—),男,硕士研究生,研究方向为电机设计与优化。

TM 307+.1

A

1673-6540(2017)02- 0110- 05

2016-07-18