基于改进自抗扰控制的永磁同步电机无传感器系统研究*

韩 晔， 厉 虹

(北京信息科技大学 自动化学院, 北京 100192)

基于改进自抗扰控制的永磁同步电机无传感器系统研究*

韩 晔， 厉 虹

(北京信息科技大学 自动化学院, 北京 100192)

针对永磁同步电机(PMSM)矢量控制无速度传感器系统的速度辨识问题，分别在系统的速度环、电流环设计自抗扰控制器替代传统的PI调节器。通过自抗扰控制(ADRC)中的扩张状态观测器(ESO)对扰动的准确估计进行速度辨识，实现系统的无传感器运行；对典型自抗扰控制器进行改进，简化模型结构并引入模糊控制算法对控制器参数进行优化。仿真结果表明： 改进ADRC比PI调节更能满足PMSM系统的高性能控制要求；与模型参考自适应相比，采用ESO观测方法在电机低速运行时的转速估计效果更好，且对电机参数变化不敏感，鲁棒性更强。

永磁同步电机； 自抗扰控制； 无速度传感器； 扩张状态观测器； 转速估计

0 引 言

永磁同步电机(Permanent Magnet Synchronous Motor， PMSM)具有多变量、非线性、强耦合的特点，要满足其在复杂系统中的应用，必须提高电机性能，克服大负载和多变扰动工况带来的影响[1]。传统的PI调节方法难以满足现代高性能电气传动系统的要求，国内外学者对此提出了多种基于非线性控制理论的策略，如反馈线性化控制[2]、神经网络控制[3]、无源控制[4]、自抗扰控制[5]等。

有速度传感器系统中，转子轴上安装机械传感器用于测量转子的速度和位置，增加了整个系统的体积和成本，降低了系统的可靠性。因此针对PMSM的无速度传感器控制是近年来的研究热点。在无速度传感器控制系统中，对电机转子速度和位置的估计方法可分为适用于中高速的开环估计法、模型参考自适应法、滑模变结构法，适用于低速的高频注入法、卡尔曼滤波法以及适用于转子初始位置估计的INFORM法等。

文献[6-7]采用滑模变结构控制进行转速估计，能有效提高电机的抗参数摄动能力，但滑模控制具有不连续开关的特点，导致系统产生抖振，影响控制精度并降低系统可靠性。文献[8-9]基于模型参考自适应(Model Reference Adaptive System，MRAS)方法估算转子速度，虽在电机中、高速运行时对转速估计准确，但在电机低速运行时受定子电阻压降影响较大，电机的低信噪比使转速估计效果不理想。文献[10]利用自抗扰控制(Active Disturbance Rejection Control, ADRC)中的扩张状态观测器(Extend State Observer, ESO)实现了PMSM无速度传感器运行，估算出的转速精度较高。但ADRC的设计较复杂，不利于加快系统响应速度，且控制器需要整定的参数很多，不易整定。文献[11-12]采用卡尔曼滤波的方法进行转速估算，对外界噪声和系统建模误差具有很强的鲁棒性，可以有效解决电机低速运行时转速估计不准确的问题。文献[13]提出了一种混合控制策略，在电机高速运行时采用滑模观测法，低速运行时则切换到高频注入法，实现了全速范围内无速度传感器运行。

本文研究基于改进ADRC的PMSM无速度传感器系统中速度观测和调节问题，在速度调节和电流调节中均采用了ADRC控制器，针对常规ADRC控制器参数较多、设计复杂的问题，对其进行了改进，并利用ESO对扰动估计值中包含转速信息的特性设计速度观测器，实现了无速度传感器系统的转速估算。通过仿真试验验证了所提出的控制策略是可行的。

1 ADRC数学模型

ADRC技术具有不依赖被控对象精确模型的特点，其最突出的特征就是把作用于被控对象的不确定因素都归结为“未知扰动”，利用对象的输入、输出信息对其进行估计和补偿，从而达到自动抗扰的目的[14]。自抗扰控制器主要由三部分组成： 非线性跟踪微分器(Tracking Differentiator， TD)、ESO和非线性状态误差反馈(Nonlinear State Error Feedback， NLSEF)。其中TD实现对系统输入信号的快速跟踪，并能从中提取出良好的微分信号；ESO是自抗扰控制器的核心，通过ESO的观测可以得到各状态变量的估计值，而且能估计出内外扰动的实时作用量并加以反馈和补偿；NLSEF是ESO和TD产生的状态量估计值间误差的非线性组合；由NLSEF的输出和ESO对总扰动的补偿构成最终的控制量。

一阶自抗扰控制器结构如图1所示。

图1 一阶自抗扰控制器结构框图

根据图1所示结构，得到一阶自抗扰控制器方程为式(1)～式(3)。

微分跟踪器：

(1)

ESO：

(2)

非线性误差反馈控制率：

(3)

其中，fal函数表示为

(4)

式中：v——系统输入信号；

v1——v的跟踪信号；

r——速度因子；

y——被控对象的输出信号；

z1——y的跟踪信号；

z2——扰动观测值；

fal(e,a,δ)——最优控制函数；

a——0～1之间的跟踪因子；

δ——滤波因子；

β01、β02——ESO输出误差校正增益；

b0——补偿因子；

z2/b0——用于补偿对象内外扰动的补偿量；

u0——经过NLSEF得到的被控对象初始信号；

u——经过补偿扰动后得到的最终控制信号。

观察式(1)～式(4)发现，一阶自抗扰控制器中需要整定的参数较多，TD中有r、a0、δ0；ESO中有β01、β02、a、δ、b0；NLSEF中有β、a1、δ1。这些参数的调整过程繁杂，不利于在工程中推广应用[15]。为了降低模型的复杂性，并优化控制器参数，需对ADRC控制器进行改进。

2 PMSM系统的ADRC设计

2.1 PMSM数学模型

基于转子磁场定向、忽略磁滞损耗的PMSM在dq轴同步旋转坐标系下的数学模型：

(5)

(6)

(7)

(8)

式中：id、iq——定子绕组d、q轴电流；

Ld、Lq——定子绕组d、q轴电感，此处选用的PMSM为表贴式电机；

R——定子电阻；

ω——转子速度；

ud、uq——定子绕组d、q轴电压；

ψf——转子永磁体产生的磁势；

p——电机极对数；

J——转动惯量；

TL——负载转矩；

B——摩擦因数。

PMSM采用id=0的矢量控制方式，分别在系统的速度调节和电流调节中设计改进的自抗扰控制器。

2.2 改进的ADRC速度调节器设计

表贴式PMSM的交直轴电感相等，即Ld=Lq，根据式(7)，转速输出方程可写为

(9)

微分跟踪器的主要作用是实现过渡过程，并从中提取微分信号。但对一阶自抗扰控制器而言，ESO只输出系统和观测扰动的跟踪信号，并没有控制对象的微分输出信号，所以TD在系统中只起到了滤波的作用。为降低模型的复杂性并减少待整定参数，可省略TD。在非线性状态误差反馈中由于fal函数的特性曲线并不平滑，易使系统在进入稳态后产生抖振，故采用线性误差控制率，即在简单的一阶系统中用适当的比例增益来代替NLSEF模块，从而减小系统计算量。状态观测器的结构保持不变，主要用来观测并补偿系统的综合扰动。综合以上考虑，构造了一种带状态观测器前馈补偿加比例增益反馈的简化一阶自抗扰控制器。一阶ADRC控制器数学模型如下。

ESO：

(10)

非线性误差反馈控制率：

(11)

式中：z1——反馈转速的状态估计；

ωr——系统反馈速度；

z2——扰动信号的观测值；

iq——经过扰动补偿后输入到q轴电流环的控制信号；

β——误差增益系数；

fal(e,a,δ)——最优控制函数；

iq0——输出信号。

工程应用中，一阶ADRC控制器中NLSEF的误差增益系数β不易调节，在多变扰动工况的条件下，该参数需要进行手动调节，不利于实际应用。因此，将模糊控制用于ADRC控制器设计中，利用模糊规则对NLSEF中的参数进行整定，以便在线修改参数，有利于控制器在工程实际中的应用[16]。

模糊控制器的输入为系统给定速度与状态观测器对反馈速度的状态估计值间的误差e和误差变化率ec，输出为NLSEF中待整定参数的修正值Δβ，在其论域上均定义7个语言子集，分别为{“负大(NB)”、“负中(NM)”, “负小(NS)”、“零(Z)”、“负小(PS)”、“负中(PM)”, “负大(PB)”}。取e和ec的论域分别为[-6，+6]、[-10，+10]，隶属度函数为高斯型，取Δβ的论域为[-0.4，0.4]，隶属度函数为三角形，模糊推理采用Mamdani算法，去模糊化算法采用平均加权法[17]。Δβ整定的模糊规则如表1所示。

表1 Δβ的模糊规则表

去模糊化后，查出修正值Δβ后代入式(12)。

β=β′+Δβ

(12)

式中：β′——NLSEF中误差增益的初始值。

改进的一阶自抗扰速度调节器框图如图2所示。

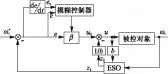
图2 改进的一阶自抗扰速度调节器框图

2.3 改进的ADRC电流调节器设计

(13)

与ADRC速度调节器的设计相似，可将TD模块省略，但电流反馈部分存在iq对d轴电流的耦合作用，若再采用简单的比例增益替代NLSEF，不利于模型的解耦控制，也会影响到模型的扰动补偿，所以要保留NLSEF部分。此时d轴电流改进的一阶ADRC控制器如下。

ESO：

(14)

非线性误差反馈控制率：

(15)

式中：z1——对实际d轴电流的状态估计；

id——d轴电流的实际输出；

z2——扰动信号的观测值；

ud——电机d轴的输出电压；

ud0——NLSEF的输出信号。

(16)

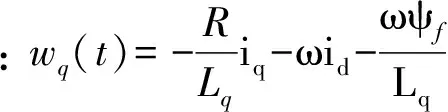
省略TD模块，考虑id对q轴电流的交叉耦合项，保留NLSEF部分，则q轴电流改进的一阶ADRC如下。

ESO：

(17)

非线性误差反馈控制率：

(18)

式中：z1——实际q轴电流的状态估计；

iq——q轴电流的实际输出；

z2——扰动信号的观测值；

uq——电机q轴的输出电压；

uq0——NLSEF的输出信号。

3 基于ESO的速度观测器

自抗扰控制器中的ESO可以实时观测系统状态，并将系统总扰动作为扩张状态观测出来。这些被观测的状态中包括系统的速度，因此可从ESO对扰动的估计中提取出系统的转速信息进行辨识。

本文利用d轴电流的ADRC控制器中ESO对扰动的估计设计速度观测器。式(13)中，令扰动为

(19)

(20)

由式(20)可知，辨识转速受电机定子电阻R和直轴电感Ld的影响，但当PMSM系统采用id=0的矢量控制方式时，定子电阻和直轴电感的变化对速度辨识的影响很小。因此，采用这种速度观测的方法能达到精度较高的速度辨识。

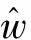
(21)

速度观测器结构如图3所示。

图3 速度观测器结构图

4 仿真验证

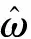
图4 基于改进ADRC的PMSM无速度传感器系统框图

在MATLAB/Simulink环境下进行仿真试验。试验所用的PMSM参数如下： 极对数p=4，定子电阻R=2.875，d、q轴电感Ld=Lq=L=8.5mH，转子磁动势ψf=0.175Wb，转动惯量J=0.8×10-4kg·m2，摩擦因数B=0。

图5是在给定转速为1300r/min，负载为2N·m的条件下，分别采用常规ADRC和改进ADRC控制器得到的转速响应曲线。

图5 转速响应曲线

图5曲线表明，在电机的速度调节中，采用带状态观测器前馈补偿加比例增益反馈的模糊ADRC控制器，以线性误差控制率替代NLSEF中的非线性fal函数，减少了系统计算量；采用模糊控制对NLSEF中的参数进行自动调节，使控制器具有更强的自适应性。此外，由于电流调节采用的是简化ADRC控制器，省略了TD模块，因此减少了控制器待整定参数，降低了模型的复杂性，缩短了系统的调节时间。

图6是当给定转速为1000r/min，带负载为2N·m起动，0.1s时突加负载到5N·m的条件下，分别采用PI控制器和改进ADRC控制器得到的转速响应曲线。

图6 转速响应曲线

图6的试验曲线表明，采用PI调节时，系统存在超调，调节时间为0.022s；而用改进ADRC时，系统无超调，调节时间为0.018s；在抗干扰试验中，PI调节时系统的转速降约为7%，恢复时间为0.012s；改进ADRC调节时系统的转速降约为0.6%，恢复时间为0.005s。可以看出，改进ADRC控制器比PI控制器有更强的抗干扰能力，转速受负载变化的影响更小，且恢复时间更短。

观察同样抗干扰试验条件下，ESO对电机速度、d轴和q轴电流的误差观测结果如图7所示。

该试验表明，ESO对系统的状态估计和系统实际值间的误差很小，说明ESO对系统中的非线性因素和扰动的估计比较精确，验证了ESO实时估计系统内外扰动作用的实用性与有效性。

图8(a)、图8(b)是在相同条件下分别采用PI控制器和改进ADRC控制器得到的d、q轴电流响应曲线。

图8中，当负载变化时采用改进ADRC控制的d、q轴电流响应曲线较稳定，受负载波动的影响小，而采用PI控制的d、q轴电流稳态误差较大，受负载变化影响更明显，表明采用改进ADRC控制时系统稳定性更好。

图7 ESO的观测误差

图8 d、q轴电流响应曲线

图9是在电机堵转时，当突加负载到3N·m的条件下，分别采用PI控制器和改进ADRC控制器时的转速响应曲线。

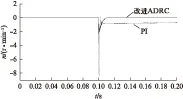
图9 转速响应曲线

图9的堵转试验结果表明，改进ADRC控制器的抗干扰能力较PI控制器更强，主要是由于ADRC中的ESO对系统未知扰动的准确估计和补偿作用，使系统对负载突变具有很强的抗干扰能力。同时，引入模糊规则对ADRC控制器的参数进行自动调节，在一定范围内优化系统参数，也进一步提高了控制器的自适应性。

图10是当给定转速降为400r/min、负载为 3N·m 条件下，PI调节时用MRAS算法进行速度辨识的实际转速响应曲线和估计转速响应曲线。

图10 基于MRAS的转速响应曲线

图11是相同条件下采用改进ADRC的ESO速度观测器进行速度辨识的转速响应曲线。

图11 改进ADRC的ESO速度观测器转速响应曲线

观察图10和图11试验结果，在电机低速运行时采用MRAS算法估计的转速响应在动态阶段的超调较大，在稳态阶段存在约3r/min的误差，而采用ESO速度观测器估计的转速能够无超调的追踪实际转速，在稳态阶段的速度辨识误差约为0.5r/min，转速估计的效果更好。这主要是因为ESO对系统扰动的准确估计和补偿。另外，与MRAS相比，ESO的速度观测器不存在参考模型不能准确反映电机自身状态的问题，且没有纯积分环节，不会产生较大的误差积累和直流漂移，低速时受定子电阻压降作用的影响小，所以在低速时的转速辨识准确性更高。

采用改进ADRC的ESO速度观测器得到的转子实际位置和估计位置的曲线如图12所示。

图12 转子位置

图12曲线表明，ESO速度观测器估计的转子位置与电机转子的实际位置比较接近，说明这种观测方法在电机低速稳态运行时对转子位置的估计是准确的。

在PMSM的实际运行过程中，电机的直轴电感受环境影响变化很小，而定子电阻却受温度、趋肤效应等因素的影响变化较大。由式(20)可知，基于ESO的速度观测器在PMSM系统采用id=0的矢量控制方式时速度辨识的效果受定子电阻变化的影响很小。图13是定子电阻为2.875时的速度辨识结果。图14(a)、图14(b)分别反映了定子电阻从2.875增大和减小后的速度辨识结果。

由图13、图14的误差曲线可知，辨识速度受定子电阻的变化影响很小，稳态误差小于2r/min，说明这种速度辨识的方法有很高的准确性和很强的鲁棒性，能有效抑制电机运行时定子电阻变化给转速估算带来的影响，可作为一种无速度传感器算法应用到PMSM系统中。

图13 定子电阻不变时的速度辨识结果

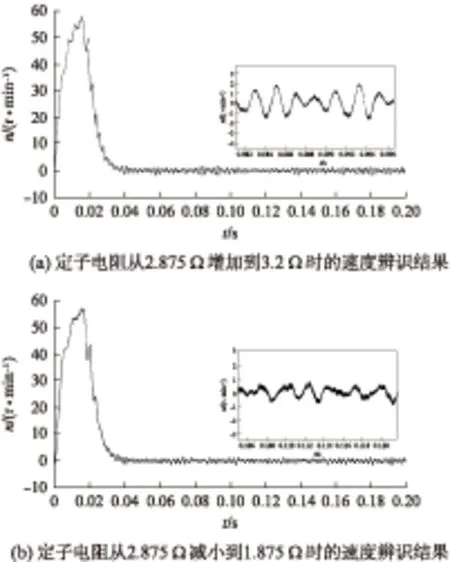
图14 定子电阻变化时的速度辨识结果

5 结 语

本文在PMSM无速度传感器系统中应用ADRC技术，分别在PMSM矢量控制系统的速度反馈和电流反馈环节中设计了改进的自抗扰控制器，并采用基于ESO的速度观测器估算转子速度和位置，以提高系统在低速时的速度估算精度和抗扰性。仿真试验表明： 改进的ADRC使PMSM系统具有响应速度快、无超调及鲁棒性强等优点，与常规ADRC相比，简化了模型结构、减少了待定参数，通过引入模糊控制使控制器具有更强的自适应性；与MRAS速度估算相比，基于ESO的速度观测器在电机低速运行时的转速估计更准确，且对电机参数的变化不敏感，抗干扰能力强，为PMSM无传感器系统速度辨识算法提供了思路。

[1] 李婉婷,厉虹.永磁同步电机自抗扰控制技术研究[J].电气传动,2015，45(9)： 20-24.

[2] 刘小河,王鹤华.基于SVPWM永磁同步电机反馈线性化控制[J].现代电子技术,2013, 36(12)： 159-162.

[3] 毛荣芳,李汉强.基于神经网络的永磁同步电机矢量控制[J].技术探讨与研究,2006,44(3)： 44- 46.

[4] 侯利民,王巍.无速度传感器的表面式永磁同步电机无源控制策略[J].控制与决策,2013,28(10)： 1578-1582.

[5] 孙凯,许镇琳,邹积勇.基于自抗扰控制器的永磁同步电机无位置传感器矢量控制系统[J].中国电机工程学报,2007,27(3)： 18-22.

[6] 高仁璟,李希伟.PMSM无传感器控制的新型滑模观测器设计[J].电机与控制应用,2014,41(11)： 7-13.

[7] HAMIDA M A, GLUMINEAU A, DE L J. High order sliding mode observer and optimum integral back-stepping control for sensor-less IPMSM drive[C]∥American Control Conference (ACC), 2013： 517-522.

[8] 张伯泽,阮毅.基于MRAS内置式永磁同步电机无位置传感器控制研究[J].电机与控制应用,2016,43(4)： 13-16.

[9] 张洪帅,王平,韩邦成.基于模糊PI模型参考自适应的高速永磁同步电机转子位置检测[J].中国电机工程学报,2014,34(12)： 1889-1896.

[10] 邵立伟,廖晓钟,张宇河，等.自抗扰控制在永磁同步电机无速度传感器调速系统的应用[J].电工技术学报,2006,21(6)： 35-39.

[11] JANISZEWSKI D. Sensor less control of permanent magnet synchronous motor based on Kalman filter[J]. Power Engineering, Energy and Electrical Drives,2011,1(7)： 11-13.

[12] 于信忠,张承瑞,李虎修,等.基于自适应扩展卡尔曼滤波器的永磁同步电机超低速控制[J].电机与控制应用,2012,39(9)： 24-29.

[13] 张海燕,刘军,兖涛,等.永磁同步电机在全速范围内的无位置传感器矢量控制[J].电机与控制应用,2014,41(7)： 1-5.

[14] 韩京清.自抗扰控制技术[M].北京： 国防工业出版社,2008.

[15] 卢达,赵光宙,曲轶龙，等.永磁同步电机无参数整定自抗扰控制器[J].电工技术学报,2013,28(3)： 27-34.

[16] 薛薇,路鸦立.永磁同步电机调速系统的模糊自抗扰控制[J].电机与控制应用,2013,40(8)： 57-65.

[17] 黄庆,黄守道,伍倩倩,等.基于模糊自抗扰控制器的永磁同步电动机伺服系统[J].电工技术学报,2013,28(9)： 294-301.

Research on Permanent Magnet Synchronous Motor Sensorless System Based on Improved Active Disturbance Rejection Control*

HANYe,LIHong

(School of Automation， Beijing Information Science & Technology University， Beijing 100192， China)

Research on the speed identification of permanent magnet synchronous motor (PMSM) vector control speed sensor less system. Designed speed-loop controller and current-loop controller based on active disturbance rejection control (ADRC) instead of the PI regulator. The speed was accurate estimated by extend state observer’s (ESO) accurate estimation of disturbance, then the sensor less speed control had been realized. The typical active disturbance rejection controller was improved, the structure of ADRC controller was simplified and fuzzy control algorithm was introduced to optimize the parameters of the controller. The simulation results showed that compared with PI regulation, the ADRC regulation could meet the requirements of the high performance control of PMSM system; compared with the model reference adaptive system (MRAS), when the motor at low speed, the speed estimation effect was better based on the ESO observation, it was not sensitive to the variation of motor parameters and the robustness was stronger.

permanent magnet synchronous motor(PMSM); active disturbance rejection control(ADRC); speed sensorless; extend state observer(ESO); speed estimation

国家自然科学基金项目(11472058)

韩 晔(1991—)，男，硕士研究生，研究方向为交流电机非线性控制。 厉 虹(1959—)，女，教授，研究方向为高性能电气传动控制系统。

TM 351

A

1673-6540(2017)02- 0033- 08

2016-07-13