欣赏学生智慧，培养数学能力

高劲松

[摘要]数学学习能力的培养不可一蹴而就，需要行之有效的方法，而发现并利用学生的智慧可以帮助学生更快地融入高中数学的学习中。如果我们可以以点带面，通过学生的一个小小的闪光点，经过一系列的训练培养让学生形成自己的学习模式。那么教学质量一定会有所提升。本文即在发现学生智慧、培养学生能力的理解基础之上，提出笔者的见解，希望能对高中数学教学有所帮助。

[关键词]高中数学；发现；数学能力；培养

欣赏学生智慧即在教学过程中教师要时常擦亮自己的眼睛。及时发现学生的闪光之处。并及时给予关注和培养。这样使学生对数学学习充满自信在高中三年的学习中保持自信的态度进行学习。提升数学学习能力。在教学过程中。教师扮演着伯乐的角色。因此我们要学会向学生抛出橄榄枝。让学生有机会展现自己的思维想法。这样我们才能去发掘每个学生的优点并将其放大。数学学习重在激励、在唤醒、在鼓舞，而赏识是教学的重要环节。下面是笔者对发掘学生智慧进行的一些分析。

欣赏学生的发现

发现是学生学习中的必经之路。学生对知识的习得就是通过不断地发现和理解进行的。学生对题目的发掘多种多样。数学题目中包含的思想也丰富多彩。因此对于不同的发现我们要先给予欣赏的眼光。再通过课本知识给予解释和修正。这样才能鼓励学生善于发现。善于提出自己的想法。让教师可以了解学生的知识掌握能力。可见欣赏学生的发现不仅仅是鼓励学生进行思考。更是对教师本身教学的一种辅助。

例如，已知函f（x）=lgx，h（x）=-（x-10）²+1，试求若f（x）=h（x），这个方程在区间[9，10]上面有几个根。教师要给学生充足的空间进行思考。再说出他们自己的想法。

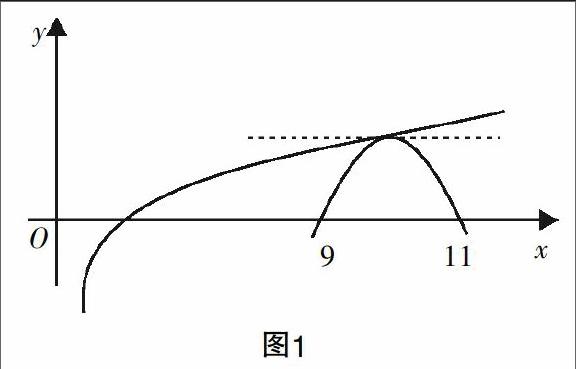
学生一：此题可以转化为两个函数图像的交点问题。如图1，发现f（10）=h（10）=1，所以只有一个交點，则上述方程只有一个根。

学生二：我觉得上述方法有所不妥。过点（10，h（10））作函数h（x）的切线发现切线是水平的，再由f（x）=lgx的图像的割线“逼近”可知此方程可能有两个交点。如图1。

听完两位学生的探讨。可见他们都运用了数形结合的方法。虽然学生二的方法有所不妥。但是对教材中切线的概念有较明确的认识。能想到“以曲代直”的方法。以化简此题的难度。这就是对学生欣赏的目光。不管什么方法总有其优点。

学生三：一定有两个根，用计算器计算得lg9.99≈0.99957<-（9.99-10）²+1。可见这两个函数的图像有两个交点。

这个发现着实可以让教师眼前一亮。数学学习正需要这种严谨的态度。

学生四：可以构造函数来进行求解。令g（x）=lgx+（x-10）²-1，之后进行求导，分析可得g'（x）在（9，10）上先负后正，且g（9）>0，g（10）=0，因此一定存在一根。

由此可见不同的学生其思维不同。看待问题的角度也多样化。如果教师能善于发现学生思维的闪光之处并加以鼓励。那么学生得到教师的认可后其在学习的过程中就有了充足的动力。学生一定会有更优秀的表现。与此同时也可以改善教师的教学方法。

欣赏学生的合作

对于学生潜力的发掘不仅仅要从知识层面进行。还要对学生的数学精神进行培养。高中数学难度增大。抽象的理论未免枯燥无味。此时更多学生喜欢借助外界的力量进行学习。通过与其他学生的合作交流一定会激发出不一样的火花。对于学生合作交流得到的成功教师一定要给予重视。因为这个过程不仅仅是学生思维能力碰撞的过程。更是团队精神的培养过程学会从其他人身上学习。学会交流。这对学生学习数学是百利而无一害的。