基于系统判别法的涡流无损检测的参数模型分析
2017-04-03赵海龙彭炜淞黄兴
赵海龙, 彭炜淞, 黄兴
(东北石油大学,黑龙江 大庆 163318)
0 引 言
无损检测技术已经广泛应用于许多工程领域[1]。有效的无损检测系统能检测结构中是否有缺陷,将测到的缺陷分类为特定类型,甚至量化缺陷细节,例如位置,大小,方向。传统的涡流无损检测使用单频正弦波作为输入信号来激励被测结构。脉冲涡流无损检测是近几年开发的新技术,其不使用单频正弦曲线,而是使用脉冲线圈激励来进行结构检查。然而,使用脉冲涡流无损检测时需要有效的分析识别技术[2]。我们应用系统识别方法来建立传递函数模型,并用模型参数来代替分析差分信号,来反映系统的结构特性的变化。还提出使用Fisher识别分析和Fisher识别方程对缺陷类型分类。
1 系统识别和Fisher判别分析
系统识别是在输入和输出数据的基础上,从一组给定的模型中,确定与被测系统等价的模型。当系统被输入信号激励,系统对输入信号的响应叫做输出信号,一般通过输入信号和系统的特点确定输出信号[3]。系统识别可以从输入输出数据中确定系统的数学模型,以及表示系统的动态行为,并且这些数学模型的参数或函数的参数可以用于表示系统特征的不同特点。例如,考虑通过二阶微分方程表示系统输入和输出之间的关系:
(1)
式中:y(t)和u(t)分别是标识系统的输入和输出,a1,a2,b1和b2是微分方程模型的参数,他们确定系统的动态特性。在频域中,微分方程模型(1)可以写成:
s2y(s)+a1sy(s)+a2y(s)=b1su(s)+b2u(s)
(2)
推出以输入输出模型为基础的传递函数,记作:
(3)
式(2)(3)中:s是拉普拉斯算子,y(s)和u(s)分别是y(t)和u(t)的拉普拉斯变换,H(s)是系统的传递函数[4]。
Fisher判别法(FDA)是一种先投影的方法[5]。Fisher 判别方程是一个与FDA判别分析相关的特定判别函数。基本思想:从两个总体中抽取具有n个指标的样本观测数据、借方差分析的思想构造一个判别函数或称判别式:y=c1x1+c2x2+…+cnxn其中系数c1、c2、…cn确定的原则是使两组间的区别最大,而使满足内部的离差最小。有了判别方程后,对于一个新的样本,将它的n个指标值代入判别方程中求出y值,然后与判别临界值进行比较,就可以判别它属于哪一类[6]。
FDA是一种非常有效的特征提取/减少维数的技术,它比诸如用于故障诊断的主成分分析(PCA)等方法,对种类之间的信息分类更具有优势。FDA特征提取以两个方阵为基础,从训练数据集合中产生类内离散度矩阵Sw和类间离散度矩阵Sb[7]。
2 基于系统分析方法的脉冲涡流无损检测
脉冲涡流无损检测采用重复的宽带脉冲激励线圈,激励线圈激发出持续衰减的磁场信号,磁场信号在导体中感应出向导体内部传播的持续衰减的涡流信号,涡流信号产生的涡流磁场作用在检测线圈上[8],检测现场产生随时间变化的瞬态电压信号。
考虑系统识别在显示系统特点和处理噪音和测量误差的能力和优势,而且在建立模型分析上主成分分析和Fisher判别方程的效率,所以提出了基于系统分析方法的脉冲涡流无损检测。
该方法的基本思路:
(1)使用系统识别技术从脉冲线圈激励和测量的涡流传感器响应建立被测系统或结构的传递函数模型,并使用传递函数模型的估计参数来反映系统或结构的特性。
(2)使用FDA从传递函数模型的估计参数提取检查系统的重要特征,并使用Fisher判别分析和最大选择的程序将检查的系统分配到表示特定工作或有缺陷条件的种类中。
为了进行该方法,需要将数据进行训练。从系统中测量的脉冲激励和相关涡流传感器响应首先用于确定系统或结构的传递函数模型。然后用FDA来从估算传递函数参数中提取系统的特征。最后,用最大选择程序从n个Fisher判别函数求解,并且将最大的Fisher判别函数值对应的有缺陷或工作条件的种类分配给被测系统。
为了解决传统无损检测的固有问题,尤其是噪音产生的干扰问题,现在很多研究人员提出先进的信号处理技术。先进的信号处理方法与传统无损检测对比,基于系统识别的脉冲涡流NDE方法不直接使用涡流传感器测量结果来执行NDE分析。相反,新方法基于通过FDA操作从被测系统或结构的识别传递函数模型的参数提取的特征进行NDE分析。因为系统的动态行为由模型参数唯一确定,所以这些参数应该比直接用传感器测量更能反映出系统的特性,通过FDA从估算模型参数中提取的特征,因此将提供一个与现场设备的物理特征相关的清晰图形。而且,因为大多数系统识别法有处理噪音和测量误差的能力,所以噪音和测量误差在分析结果上也可以有效的减少。
为了评估新提出的无损检测法的性能,所以从不同缺陷条件下的两组样品的涡流无损检测收集实验数据进行分析。
3 实验过程及结果分析
3.1 实验设置和实验样本
本实验有两组铝样本,第一组有三个样本属于三类缺陷—没有缺陷、20 mm表面裂缝缺陷、40 mm表面裂缝缺陷。第二组样本中,共有23个样本,12个样本属于金属缺陷程度在2 mm到10 mm;5个样本属于表面缺陷现在2 mm、4 mm、6 mm、8 mm;6个样本属于亚表面缺陷在2 mm、4 mm、6 mm、8 mm范围内。
在对第一组样本进行试验测试中,由于激励和响应的线性关系覆盖范围如图4,所有样本用脉冲幅度分别为50 mA、100 mA、150 mA、200 mA、250mA、300 mA、350mA、400 mA、450mA、和500 mA的信号u(t)激励。产生30个激励和响应数据,但只有信号为200 mA、250mA、300 mA、350 mA、400 mA的15个数据可用。对于这15个输入输出数据,其中缺陷的样本(数据1,2,3)获得3个数据, 20 mm表面裂纹缺陷(数据4,5,6)中获得3个数据和40 mm便面裂纹缺陷(数据7,8,9)样本获得3个数据,这些当作训练数据集。其余样本(数据10~11是从没有缺陷样本中获得,数据12~13是从20 mm表面裂纹缺陷获得,数据4~15是从40 mm表面裂纹样本中获得的)当作新数据,通过这些数据分类样本的情况来评估该方法的表现。
对第二组样本进行试验测试,所有23个样本用500 mA的脉冲信号进行激励。激励信号和相关响应是从1 MHz频率中取样,一共23个输入输出数据。对第二组样本进行试验测试,所有23个样本用500 mA的脉冲信号进行激励。激励信号和相关响应是从1 MHz频率中取样,一共23个输入输出数据。对于23个出入输出数据,10个金属损耗缺陷样本(数据1~10),三组表面裂纹缺陷样本(数据11~13),四组亚表面裂纹缺陷(数据14~17),这些数据当作训练数据组。其他数据中,有两组是损耗缺陷(数据18,19),两组表面裂纹缺陷(数据20,21),两组亚表面裂纹(数据22,23)是新数据,通过这些数据分类样本的情况来评估该方法的表现。
3.2 实验结果分析
3.2.1对第一组铝样本结果分析
对于第一组样本,传递函数模型是:
(4)
用于系统识别建模过程。传递函数(4)可以展开为:
(5)
该传递函数模型与函数(3)的传递函数模型相同。
如图1所示,系统识别法对第一组三个样本收集到的数据K,τ,T1,T2进行估算。
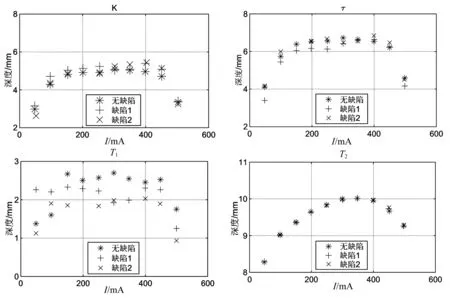
图1 第一组样本系统识别结果
如图2所示,9个FDA向量和明确指出Fisher判别分析在三个不同的区域(第一区域的z(1)-z(3),第二区域的z(4)-z(6)和第三区域的z(7)-z(9))独立分析9个向量。利用FDA算法对脉冲涡流响应数据进行处理,算法过程中,选择贡献率最大的两个特征量(即特征量1和特征量2,无量纲)对应的特征向量组成投影矩阵。在Fisher判别分析的二维坐标系中分析,每一个区域表示一个缺陷条件类型。除了9个训练向量,其他6个新的数据也分别正确放置到训练数据所在的区域,也就是其相应的缺陷。
实际上,这种现象是符合基于Fisher判别函数的最大选择的结果。显然,最大选择程序将新数据分配到正确的分类中。因此,对来自第一组样本的实验数据的分析验证了该新的无损检测方法的有效性。
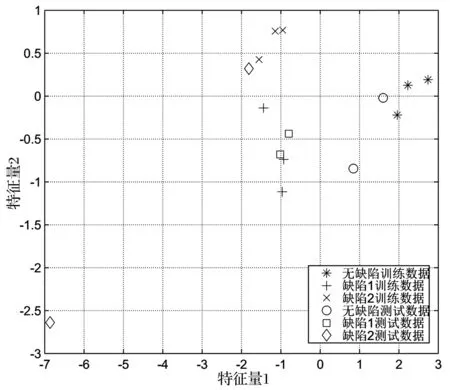
图2 第一组样本测试数据的FDA向量估值
3.2.2对第二组铝样本结果分析
对于第二组样本传递函数是:
(6)
用于系统识别建模过程。方程(6)写作:
(7)
该传递函数模型与函数(3)的传递函数模型相同。
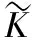
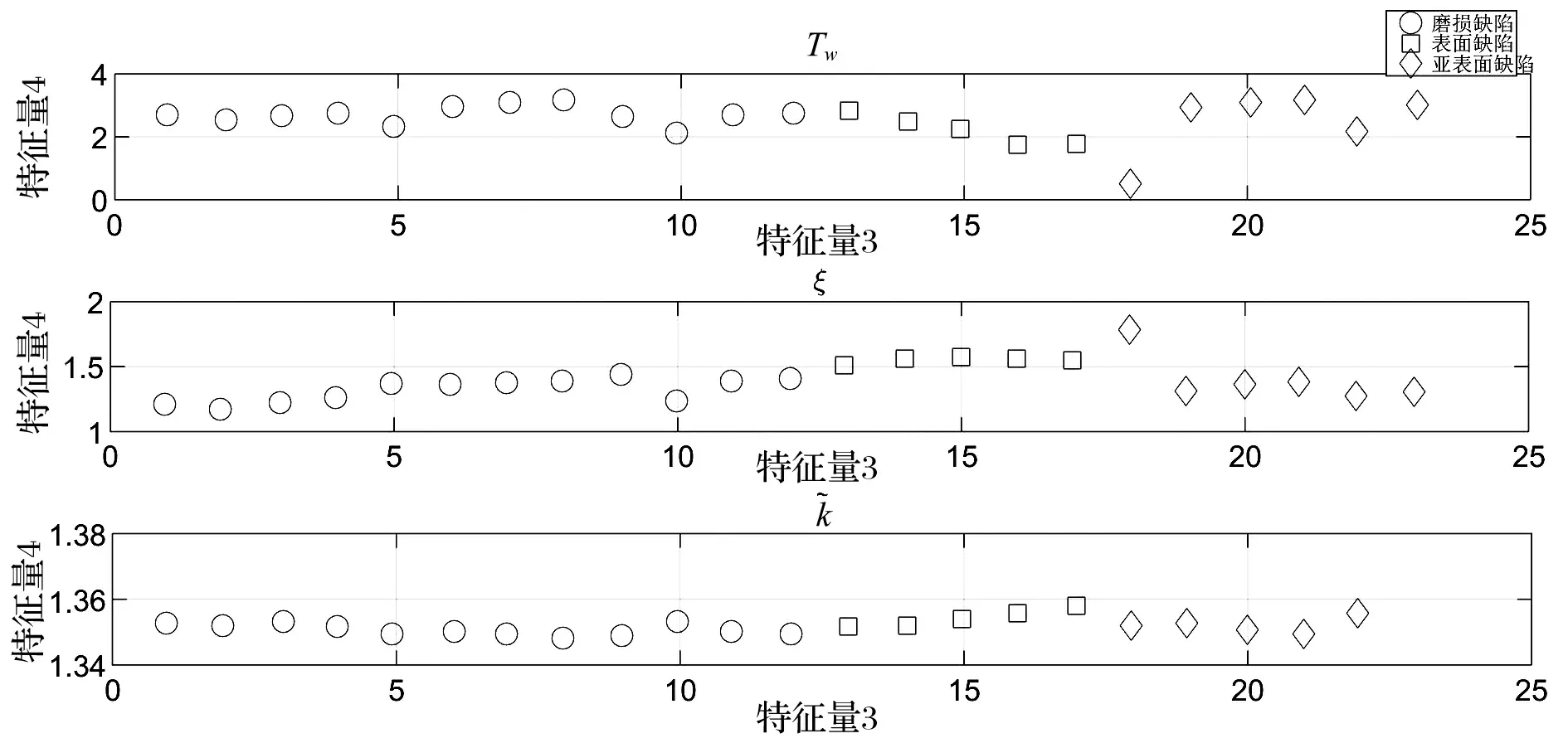
图3 第二组样本系统识别结果
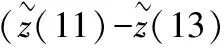
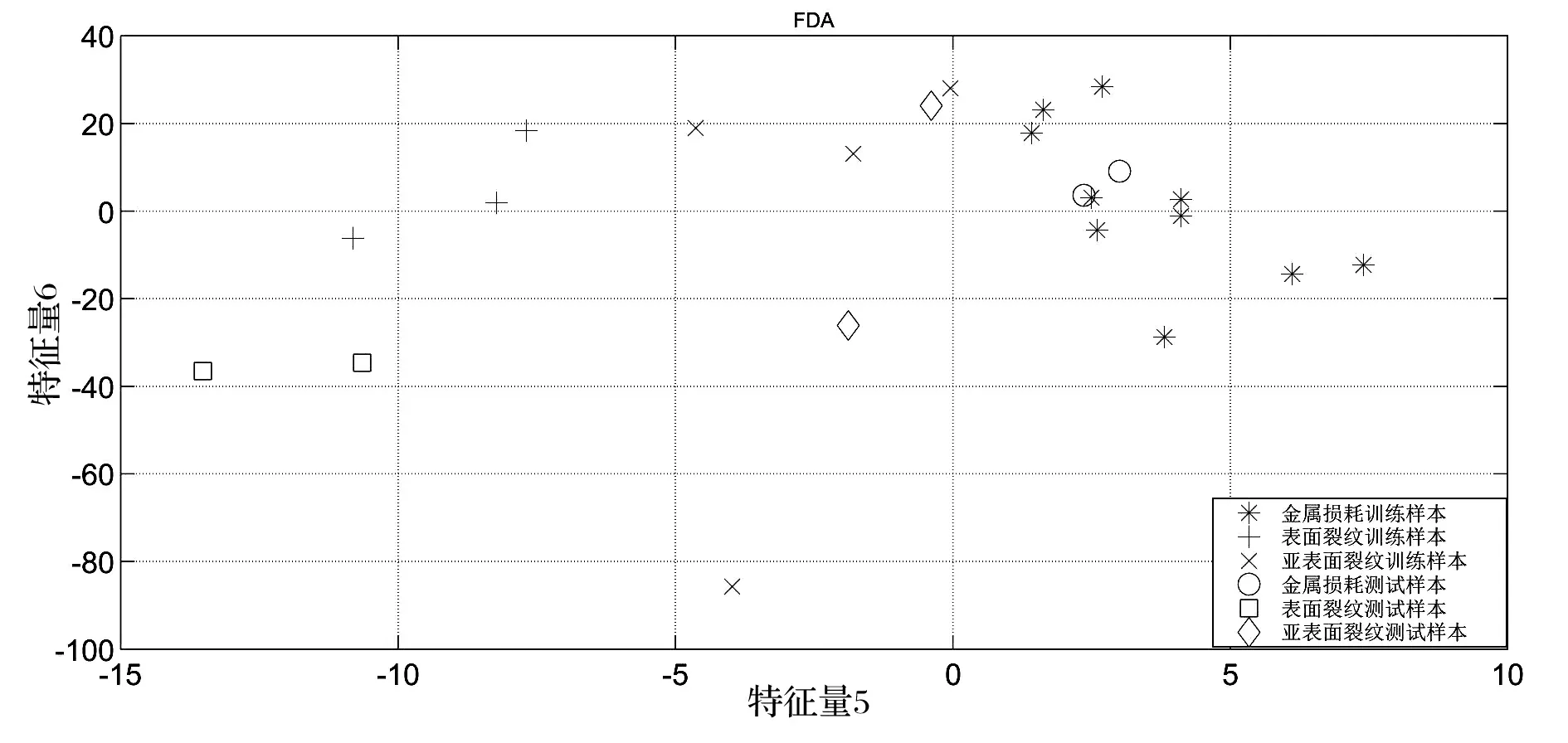
图4 第二组样本测试数据的FDA向量估值
4 结束语
脉冲涡流无损检测技术在工程领域中应用非常广泛。与传统的涡流检测直接分析传感器获取的电压不同,脉冲涡流技术依靠对激励所产生的响应进行分析。与广泛应用的差分信号分析相比,传递函数模型能更好的描述系统能够的特点,可以更好的显示出系统的动态特性的真实机理,还可以减少测量误差和噪音的影响。此外,该方法还使用Fisher判别分析(FDA)和相关Fisher判别函数识别传递函数模型参数的缺陷模型分类。这使得缺陷或工作类型的训练数据中的信息可以有效的用于评估新数据的工作条件。该方法用于分析两组铝样本的无损检测结果,结果验证了该方法的有效性,并展示了新方法在工程应用中的潜力。
参考文献:
[1] KIM J,YANG G,UDPA L,et al.Classification of pulsed eddy current GMR data on aircraft structures[J].NDT&E International,2010,43(2):141-144.
[2] 王三胜,易忠,侯化安,等. 脉冲涡流无损检测技术及其用于航空航天材料缺陷检测的研究进展[J]. 航天器环境工程,2015,32(3):307-312.
[3] ANGANI C,PARK D,KIM G,et al.Differential pulsed eddy current sensor for the detection of wall thinning in an insulated stainless steel pipe[J].Journal of AppliedPhysics,2010,107(9):248-252.
[4] 武新军,张卿,沈功田. 脉冲涡流无损检测技术综述[J]. 仪器仪表学报,2016,37(8):1698-1712.
[5] 何赟泽.电磁无损检测缺陷识别与评估新方法研究[D].北京:国防科技大学,2012.
[6] 胡祥超. 集成涡流无损检测系统设计与关键技术研究[D].北京:国防科学技术大学,2012.
[7] 黄琳.基于脉冲滿流信号频谱分析的缺陷表征方法[D].厦门:厦门大学,2012.
[8] 闫向阳. 方向性脉冲涡流无损检测研究[D].无锡:江南大学,2013.
