居民负荷需求响应参与度的物理影响因素分析
2017-04-03李章允王钢汪隆君陈小闽
李章允, 王钢, 汪隆君, 陈小闽
(华南理工大学 电力学院,广东 广州 510640)
0 引 言
随着智能电网快速发展,需求响应(Demand Response, DR)成为消纳可再生能源和促进电力供需平衡的关键技术[1-2]。研究表明[3-4]:发展DR至少能避免14%的新建发电资源;2014年欧洲大陆居民用户DR潜力高达37GW。需求响应是电力用户自发自愿的行为,具有不确定性。将量化用户参与需求响应不确定性的概率大小定义为DR参与度。若仅有62%居民用户参与,只能实现其DR潜力的一半[5]。可见,DR参与度是评价用户群体响应参与积极性与需求响应策略合理性的重要指标,也是电力相关部门更新DR策略的参考依据。
国内外围绕DR的研究重点在DR机制、DR负荷模型、DR策略、DR成本与效益和DR信息系统集成等。DR按照响应信号可分为价格型和激励型,两者可建立统一范式的DR模型[6]。根据负荷响应特征将用户聚类,并与用户签订合约建立DR负荷模型[7]。将DR负荷模型集成到发电计划决策或负荷聚合商决策形成DR策略[8],以实现发电成本最小、系统网损最小、弃风光电量最小等目标。DR不仅能给用户和电网带来直接收益,还能给电力工业可持续发展提供长期信号及环保效益[9]。支持源网荷互动的新一代电力调度系统和开放式自动需求响应通信规范[10]为DR的实行提供了集成标准。然而对DR行为不确定性的研究鲜有报道。居民用户参与DR行为相关性差,但其数量大易形成规模效应。为突出DR参与度的差异性,居民负荷更具有研究价值。需求响应涉及多种因素,其中物理因素对DR参与度的影响相对容易量化分析。
为此,提出居民负荷需求响应参与度的物理影响因素分析模型及其算法。以DR参与度最大为目标建立需求响应概率优化模型;当响应范围足够大时,将所提概率优化模型等效成一系列混合整数规划问题实现高效求解;量化物理影响因素对DR参与度的作用,分析影响趋势及程度。以含6 000户的居民小区为实例分析验证了所提模型及其算法。
1 数学模型
1.1 需求响应概率优化模型
用户在不大幅降低自身用电舒适度的前提下决定是否参与DR,其不确定性体现在参与DR的行为上。因此,需求响应行为分析的基础为概率优化建模。一定时期内用户能参与DR的负荷总量是固定的,DR参与度反映了实际响应量超过响应期望的概率。在某种DR策略下,以DR参与度最大为目标,约束条件包括用户补贴总费用受成本约束、用户节约电费不小于期望值等。需求响应概率优化模型可表示为:
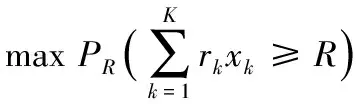
(1)

(2)
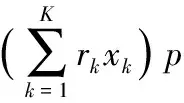
(3)
式中:PR为负荷响应总量不低于响应期望值R的概率,其累积分布直接影响决策结果;rk和xk分别为用户k的响应量和是否被选择参与需求响应的标志,xk为0-1变量,1和0分别表示被选择和不被选择;K为用户数;C表示实施DR策略的成本限值;ck、Pk分别为用户k参与DR的补贴费用和节省电费期望值;p为电价。
需求响应概率优化模型以负荷响应量为基础,涉及负荷响应模型。居民负荷中参与DR的主要是温控类负荷(包括空调和热水器),其电量占比超过50%[11]。因此,对空调和热水器的响应进行建模。
1.2 空调负荷响应模型
对于制冷空调来说,提高空调设置温度能有效降低用电量,被用来鼓励用户参与有序用电和错峰用电,其参与DR电量取决于用户k空调设置温度的变化差值ΔTr,k。若时刻t室外温度为To,k,t,空调初始设置温度和参与DR设置温度分别为Tr,k和Ts,k,其关系如下:
To,k,t≥Ts,k
(4)
ΔTr,k=Ts,k-Tr,k
(5)
用户k空调负荷响应量可表示为:
ra,k=ak,tΔTr,k
(6)
式中:ak,t为制冷敏感度系数,可通过用电量的历史数据对下式作线性回归得到。
lk,t=ak,t(To,k,t-Tr,k)+lk0,t+ek,t
(7)
式中:lk,t为用户k时刻t的空调耗电量;lk0,t为初始设置温度的空调耗电量负荷;ek,t为随机变化量。
ΔTr,k与当前时刻的室内温度Ti,k紧密相关,ΔTr,k和Ti,k表示为[12]:
ΔTr,k=fa(Ti,k)
(8)

(9)
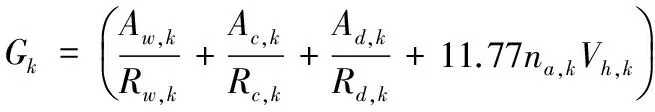
(10)
Δck=Ca,kVh,k
(11)
式中:fa为空调智能调节器函数;Gk为用户k房间吸热率,单位为W;Δck为用户k房间温度改变1 ℃时所需的能量,单位为Wh/℃;Δta,k为用户k当前时刻与前一时刻的时间差;Aw,k、Ac,k、Ad,k和Rw.k、Rc,k、Rw,k分别为用户k墙壁、天花板、窗户的面积和隔热系数;na,k为用户k房间换气次数;As,k、HS,k、Hp,k分别为用户k南向窗户面积、太阳辐射功率、人体散发热量;SH,k为用户k太阳得热系数,是通过玻璃,门窗或幕墙构件成为室内得热量的太阳辐射热与投射到门窗或幕墙上的太阳辐射热的比值,无量纲;Ca,k、Vh,k分别为空气比热容和房间体积。
1.3 热水器负荷响应模型
热水器可在不同档位对应的功率下运行,参与DR用电量变化取决于前后档位所对应运行功率的调整,因此响应模型为:
rw,k=(Pw,k0-Pw,k)ηktw,k
(12)
式中:ηk和tw,k分别为用户k热水器使用效率和使用时间;Pw,k0和Pw,k分别为参与DR前后时刻热水器的运行功率。Pw,k与水箱水温Tu,k有关,两者的关系以及Tu,k可表示为:
Pw,k=fw(Tu,k)
(13)
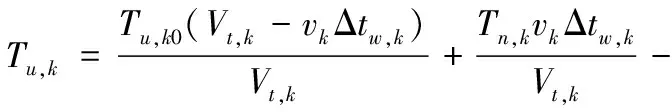
(14)
式中:fw为热水器智能调节器函数;Tu,k0和Tu,k分别为热水器前后时刻的水温;Δtw,k为前后的时间差;Tn,k为进水温度;Vt,k、At,k和Rt,k分别为热水器水箱的体积、表面积和隔热系数;vk为热水流速。
综上所述,居民负荷响应量rk为空调负荷响应量与热水器负荷响应量之和,即:
rk=ra,k+rw,k
(15)
2 模型求解方法
按照背包问题[13]的定义,所提需求响应概率优化模型的表达形式与背包问题一致,又因为响应行为存在随机性,所以模型可抽象为随机背包问题(stochastic knapsack problem),为NP-难问题。目前求解随机背包问题通常采用蚁群算法、粒子群算法、禁忌搜索算法、遗传退火算法等启发式搜索算法。算法解不稳定性和早熟现象使上述方法距工程应用还有较大差距[14]。因此,须探寻一种有效的求解方法,不仅能高效稳定获得全局最优解,还可以调和求解速度与精度的矛盾。
大量统计表明,当用户数量K足够大时,根据中心极限定理,用户总响应量呈正态分布:
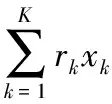
(16)
式中:N代表正态分布;均值为μ=μTx,方差为σ2=xTΣx;μ是元素为用户响应量rk的列向量;Σ为协方差矩阵,元素为响应量rj和rk之间的协方差。
为此,需求响应的概率优化求解问题转变成了正态分布的概率求解,响应概率优化模型目标函数可转换为:

(17)
s.t.(μ,σ2)∈H
(18)
H=Conv{(μ,σ2):x∈Hx,μ=μTx,σ2=xT∑x}
Hx={x:x∈{0,1}K,cTx≤C,μTx≥R,xT∑x≥0}(19)
式中:H表示(μ,σ2) 的可行域,Conv表示凸集,Hx表示x的解空间。用户实际参与DR完全凭借自己的意愿,互不干扰,因此可认为用户响应行为是相互独立的,即Σ为对角矩阵[σ2=(Σ11,…,ΣKK)]。
式(17)为μ和σ2的非线性函数,为便于求解可构造与式(17)有相同最优解(μ*,σ*2)的线性函数,从而将式(17)的模型转化等效成一系列混合整数规划问题[5],具体转换等效与求解过程详见文献[5]。
至此,所提响应概率优化模型所属的随机背包问题转换成了一系列混合整数规划问题,极大地降低了问题的求解难度,保证了最优解的全局唯一性。混合整数规划问题可用MATLAB自带的规划问题求解函数进行快速高效求解。
3 算例分析
选取含有6 000户的某居民小区作为研究对象,空调和热水器参数分布如表1和表2所示。基于K-means聚类算法对居民的用电抽样曲线聚合为6类,聚类质心即为典型用户,分别称为用户1、用户2、用户3、用户4、用户5和用户6。下面分析居民负荷响应量及其物理影响因素的算例测试均在:Intel(R) Core(TM) i7-3770 CPU @3.40 GHz,16.0GB RAM的Windows 7 SP1 64bit环境下进行。

表1 室内温度计算所需参数

表2 混合水温度计算所需参数
3.1 需求响应分析
基于空调负荷用电量与外界温度历史数据[15]对式(7)作线性拟合得到ak,t。假设用户空调前一时刻温度Tp,k均为20 ℃,Δta,k均等于1h。用户室内温度越高,空调参与DR温度变化越小,空调智能调节器函数fa(·)为:

(20)
基于空调负荷响应模型与空调调节器函数求得Ti,k和ΔTr,k绘制于图1(a)。
典型用户的Pw,k0和Tu,k0如图1(b)所示,时间间隔Δtw,k=1 h。某型号储水式多功率热水器共有7个运行档位,最大功率为7.5 kW,各档功率分别为0 kW、2.0 kW、3.0 kW、4.0 kW、5.0 kW、6.0 kW、7.5 kW。Tu,k较大时智能调节器调低热水器运行功率,调节函数fw(·)为:
(21)
基于热水器负荷响应模型与热水器调节器函数求得Tu,k和Pw,k绘制于图1(c)。
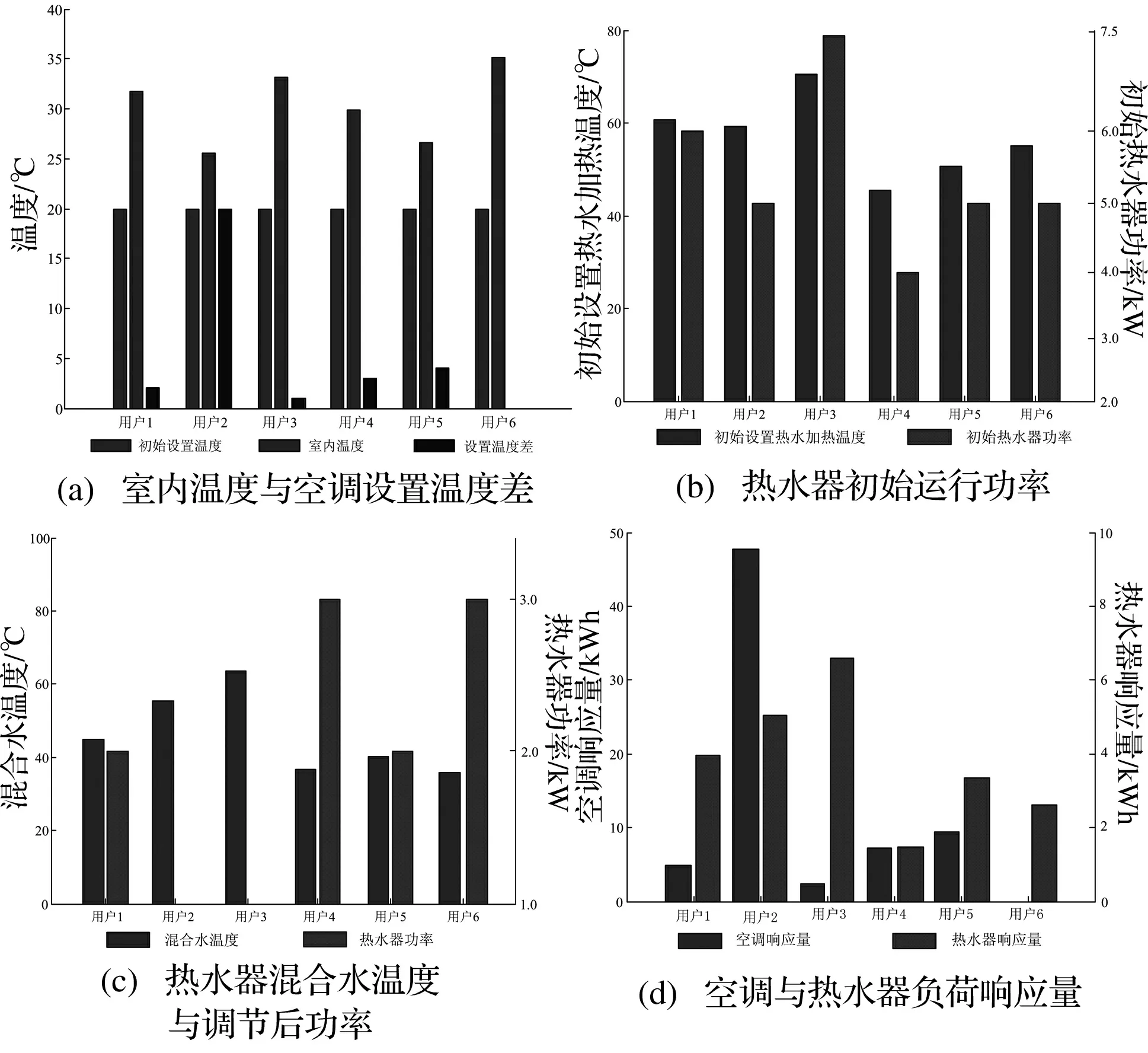
图1 典型用户需求响应
将ΔTr,k和Pw,k分别代入式(6)和式(12)获得空调和热水器需求响应量,绘制于图1(d)。
由图1可见:(1)ΔTr,6=0,即ra,6=0。因为用户6的室内温度高达35.1 ℃,为满足用户舒适度可不调整空调设置温度;(2)其它用户均存在响应量,其中,Ti,2=25.6 ℃致用户2关闭空调,此时满足舒适度的同时参与DR量最大;(3)用户2和用户3的水温分别达到55.4 ℃和63.9 ℃,热水器不必继续加热即可满足热水需求,Pw,2=Pw,3=0;用户4和用户6的水温分别为36.8 ℃和35.8 ℃,热水器还需在第3档运行,Pw,4=Pw,6=3.0 kW。(4)rw,3=6.68 kWh,rw,4=1.44 kWh,rw,3/rw,4>4说明热水器负荷DR潜力差异较大。
设该小区实行的DR项目成本C=60万元,居民电价p=0.60元,项目的DR总量期望值R=40 000 kWh。求解所提优化模型得到最优解x*,代入式(17)可得居民负荷总响应量分布均值μ=μTx= 58 625 kWh,标准差σ=xTΣx=14 639 kWh,用户参与数∑xk=1 612,最大需求响应概率为PR=89.84%。
3.2 物理影响因素分析
进一步量化各物理因素对DR概率的影响,选取了6个因素:SH、Vh、tw、Vt、As和v。
分别取SH为0.15、0.3、0.4、0.5、0.65、0.8,Vh为425、453、481、510、538、566,所得PR(·)如图2所示。

图2 SH和Vh对响应概率的影响
由图2可得:(1)SH增大,PR减小。这是因为SH增大时,从房间窗户处将得到更多的太阳热量,室内温度受外界太阳热量的影响更大,用户调节空调负荷的可能性变小,因此PR减小。(2)Vh增大,PR增加。Vh增大时,用户更倾向于调节空调到较适宜状态,PR更大。(3)两者对比,SH比Vh对PR有更显著的影响。
分别取tw为1.6、1.7、1.8、1.9、2.0、2.1,Vt为20、30、40、50、60、70、80,所得PR(·)如图3所示。

图3 tw和Vt对响应概率的影响
观察图3得:(1)随着tw和Vt的增大,PR均呈现出增加的趋势;(2)高容量Vt对PR影响并不明显。这是因为Vt较大时,有热水没有被充分利用,用户不必继续加热;(3)Vt于较小容量范围增大时,PR增加较快,Vt较小时储存热水能力有限,需选择调增功率提高水温满足用水要求;(4)显然,热水器使用时间增加,rw和PR增加。
取As值分别为5.57、6.50、7.43、8.36、9.29、10.22、11.15,v分别为8、9、10、11、12,所得PR(·)如图4所示。

图4 As和v对响应概率的影响
由图4可知:(1)随着As增大,PR减小;这是因为空调房间向阳面积大,室外太阳热量对室内温度影响程度变大,空调调节能力受到制约;(2)v增加,PR减小。这是因为热水使用速度加快,此时为保证热水供应,热水器不但无法降低功率运行,反而可能提高功率运行,导致PR减小。
4 结束语
提出了以居民负荷DR参与度最大为目标的需求响应概率优化模型及其求解方法,量化物理因素对响应概率的影响趋势及程度。以含6 000户的居民小区为实例进行分析验证,得到结论:
(1)所提模型的DR参与度的高低有助于评价用户群体的响应积极性与需求响应策略合理性,可作为更新DR策略的参考依据。
(2)最优概率随物理因素的变化趋势各异,随Vh、tw、Vt增大而升高,随SH、As、v增大而降低。
(3)物理影响因素中,太阳得热系数SH和热水器使用时间tw对PR的影响程度最为显著,变化幅度分别超过4%和6%。
后续研究将对负荷参与DR的调节函数fa(·)和fw(·)作深入讨论分析。
参考文献:
[ 1 ] 盛万兴,史常凯,孙军平,等.智能用电中自动需求响应的特征及研究框架[J].电力系统自动化,2013,37(23):1-7.
[ 2 ] JUAN MANUEL ROLDAN FERNANDEZ, MANUEL BURGOS PAYAN, JESUS MANUEL RIQUELME SANTOS, et al. Renewable generation versus demand-side management. A comparison for the Spanish market[J]. Energy Policy, 2016, 96(9): 458-470.
[ 3 ] NING ZHANG, ZHAOGUANG HU, CECILIA SPRINGER, et al. A bi-level integrated generation-transmission planning model incorporating the impacts of demand response by operation simulation[J]. Energy Conversion and Management, 2016, 123(9): 84-94.
[ 4 ] HANS CHRISTIAN GILS. Assessment of the theoretical demand response potential in Europe[J]. Energy, 2014, 67(4): 1-18.
[ 5 ] JUNGSUK KWAC, RAM RAJAGOPAL. Data-Driven Targeting of Customers for Demand Response[J]. IEEE Transactions on Smart Grid, 2016, 7(5): 1-9.
[ 6 ] BABOLI P T, EGHBAL M, MOGHADDAM M P, et al. Customer behavior based demand response model[C]// Power and Energy Society General Meeting. IEEE, 2012:1-7.
[ 7 ] XIAN HE, NICO KEYAERTS, ISABEL AZEVEDO, et al. How to engage consumers in demand response: A contract perspective[J]. Utilities Policy, 2013, 27(12): 108-122.
[ 8 ] 高赐威,李倩玉,李慧星,等.基于负荷聚合商业务的需求响应资源整合方法与运营机制[J].电力系统自动化,2013,37(17):78-86.
[ 9 ] M FERA, R MACCHIAROLI, R IANNONE, et al. Economic evaluation model for the energy Demand Response[J]. Energy, 2016, 112(10): 457-468.
[10] 高赐威,梁甜甜,李慧星,等.开放式自动需求响应通信规范的发展和应用综述[J].电网技术,2013,37(3):692-698.
[11] 阳小丹,李扬.家庭用电响应模式研究[J].电力系统保护与控制,2014,42(12):51-56.
[12] SHENGNAN SHAO, MANISA PIPATTANASOMPORN, SAIFUR RAHMAN. Development of Physical-Based Demand Response-Enabled Residential Load Models[J]. IEEE Transactions on Power Systems, 2013,28(2):607-614.
[13] 贺毅朝,王熙照,李文斌,等.求解随机时变背包问题的精确算法与进化算法[J].软件学报,2017,28(2):185-202.
[14] TING YEE LIM. Mohammed azmi al-Betar, ahamad tajudin khader. Taming the 0/1 knapsack problem with monogamous pairs genetic algorithm[J]. Expert Systems With Applications, 2016, 54(7): 241-250.
[15] XIAONING XU, GONGSHENG HUANG, HANWEI LIU, et al. The study of the dynamic load forecasting model about air-conditioning system based on the terminal user load[J]. Energy and Building, 2014, 94(5): 263-268.
