初中数学几何线段及线段和、差的最值问题探析

李蓉

【摘 要】初三总复习中，我们发现很多中考真题卷或模拟卷里经常出现求线段最值或线段和差最值等问题，而学生对这种题型经常无从下手，感觉特别难。其实初中阶段这种类型的问题最终基本上都能转化为以下三种类型：①利用两点之间线段最短求最短路徑或线段的最小值；②利用垂线段最短求解；③利用三角形三边关系（三角形任意两边之和大于第三边，任意两边之差小于第三边）当三点共线时取得最值。

【关键词】线段最值线段和最小；线段差最大转化定边

一、一般处理方法

（一）常用定理

（1）两点之间，线段最短（已知两个定点时）

（2）垂线段最短（已知一个定点、一条定直线时）

（3）三角形三边关系（已知两边长固定或其和、差固定时）

PA+PB最小，需转化，使点在线异侧

|PA-PB|最大，需转化，使点在线同侧

具体例题分析

类型一 利用两点之间线段最短

1.立体图形平面展开图求最短路径

例1.有一圆柱体如图，高4cm，底面半径5cm，A处有一蚂蚁，若蚂蚁欲爬行到C处，求蚂蚁爬行的最短距离。

试题分析：此题为常规题型，碰到立体图形中的最短路径问题把它展开成平面图形再利用两点之间线段求解即可。

解：AB = 4，

BC为底面周长的一半

即BC = 5π

AC = =

=

答：蚂蚁爬行的最短距离为cm。

2.通过作轴对称求距离之和的最小值

例2：如图，∠AOB=30°，∠AOB内有一定点P，且OP=10.在OA上有一点Q，OB上有一点R.若△PQR周长最小，则最小周长是（ ）

A.10 B.15 C.20 D.30

试题分析：此题出现一个定点两条定直线，所以我们是通过这个定点分别关于这两条直线作对称点，再根据三角形三边关系，最终转为两点之间线段最短来处理。

解：设∠POA=θ，则∠POB=30°﹣θ，

作PM⊥OA与OA相交于M，并将PM延长一倍到E，即ME=PM.

作PN⊥OB与OB相交于N，并将PN延长一倍到F，即NF=PN.

连接EF与OA相交于Q，与OB相交于R，再连接PQ，PR，

则△PQR即为周长最短的三角形.

∵OA是PE的垂直平分线，

∴EQ=QP；

同理，OB是PF的垂直平分线，

∴FR=RP，

∴△PQR的周长=EF.

∵OE=OF=OP=10，

且∠EOF=∠EOP+∠POF

=2θ+2（30°-θ）=60°，

∴△EOF是正三角形，∴EF=10，

即在保持OP=10的条件下△PQR的最小周长为10.

故选A.

3.利用平移求线段和的最小值

例3：荆州护城河在CC'处直角转弯，河宽相等，从A处到达B处，需经过两座桥DD'、EE'，护城河及两桥都是东西、南北方向，桥与河岸垂直.如何确定两座桥的位置，可使A到B点路径最短？

试题分析：由于含有固定线段“桥”，导致不能将ADDEEB通过轴对称直接转化为线段，需要构造平行四边形将AD、BE平移至DF、EG，即可得到桥所在位置

解：作AF⊥CD，且AF=河宽，作BG⊥CE，且BG=河宽，连接GF，与河岸相交于E、D，作DD、EE即为桥

证明：由做法可知，AF∥DD，AF=DD，则四边形AFDD为平行四边形

于是AD=FD

同理，BE=GE

由两点之间线段最短可知，GF最小

即当桥建于如图所示位置时，ADDEEB最短

二、利用垂线段最短求最值

1.通过转移点，转化为一个定点到一条定直线的距离的最小值

例1：如图，在锐角△ABC中，AB=6，∠BAC=60°，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是（ ）

A.3 B. C. D.6

试题分析：此题，两条线段涉及到三个点，其中B为定点，另外两个点均为动点，但通过角平分线这个条件可以把BM转化成关于线段AD对称的线段EM. 从而把两条线段之和的最值转化为点E到直线AB的最短距离。

解：在AC上取一点E，使得AE=AB，过E作EN⊥AB于N′，交AD于M，连接BM，BE，BE交AD于O，则BM+MN最小（根据两点之间线段最短；点到直线垂直距离最短），

∵AD平分∠CAB，AE=AB，

∴EO=OB，AD⊥BE，

∴AD是BE的垂直平分线（三线合一），

∴E和B关于直线AD对称，

∴EM=BM，

即BM+MN′=EM+MN′=EN′，

∵EN⊥AB，

∴∠ENA=90°，

∵∠CAB=60°，

∴∠AEN′=30°，

∵AE=AB=6，

∴AN=AE=3，

在△AEN中，由勾股定理得：EN=，

即BM+MN的最小值是.

故选B.

2.通过勾股定理转移线段转化为垂线段最短

例2. 如图，△ABC中，∠BAC=60°，∠ABC=45°，AB=2，D是线段BC上的一个动点，以AD为直径画⊙O分别交AB，AC于E，F，连接EF，则线段EF长度的最小值为.

试题分析：此题由于E、F两点均为动点，若按常规思路直接求其最值感觉无从下手，而此时如能转化成其他与之相关的线段直径，则问题就迎刃而解了 由垂线段的性质可知，当AD为△ABC的边BC上的高时，直径最短。

解：由垂线段的性质可知，当AD为△ABC的边BC上的高时，直径最短，

如图，连接OE，OF，过O点作OH⊥EF，垂足为H，在Rt△ADB中，∠ABC=45°，AB=，

∴AD=BD=1，即此时圆的直径为1，

∵∠EOF=2∠BAC=120°，

而∠EOH=∠EOF，

∴∠EOH=60°，

在Rt△EOH中，EH=OE·sin∠EOH=·sin60°=，

∵OH⊥EF，

∴EH=FH，

∴EF=2EH=，

即线段EF长度的最小值为.

故答案为.

3.通过三角形全等相似等转移线段转化为垂线段最短

例3.已知梯形ABCD，AD∥BC，AB⊥BC，AD=1，AB=2，BC=3，

问题1：如图1，P为AB边上的一点，以PD，PC为边作平行四边形PCQD，请问对角线PQ，DC的长能否相等，为什么？

问题2：如图2，若P为AB边上一点，以PD，PC为边作平行四边形PCQD，请问对角线PQ的长是否存在最小值？如果存在，请求出最小值，如果不存在，请说明理由.

问题3：若P为AB边上任意一点，延长PD到E，使DE=PD，再以PE，PC为边作平行四边形PCQE，请探究对角线PQ的长是否也存在最小值？如果存在，请求出最小值，如果不存在，请说明理由.

问题4：如图3，若P为DC边上任意一点，延长PA到E，使AE=nPA（n为常数），以PE、PB为边作平行四边形PBQE，请探究对角线PQ的长是否也存在最小值？如果存在，请求出最小值，如果不存在，请说明理由。

试题分析：此题难度很大，P、Q两点也均为动点，而且此题要转化的线段隐藏得更深，需要在复杂图形中挖掘线段的等分点，从而转化成线段PG的整数倍，才最终变成动点到定直线的线段中垂线段最短的问题。

解：问题1：∵四边形PCQD是平行四边形，

若对角线PQ、DC相等，则四边形PCQD是矩形，

∴∠DPC=90°，

∵AD=1，AB=2，BC=3，

∴DC=2，

设PB=x，则AP=2-x，

在Rt△DPC中，PD2+PC2=DC2，即x2+32+（2-x）2+1=8，

化简得x2-2x+3=0，

∵△=（-2）2-4×1×3=-8<0，

∴方程无解，

∴对角线PQ与DC不可能相等.

问题2：如图2，在平行四边形PCQD中，设对角线PQ与DC相交于点G，

则G是DC的中点，

过点Q作QH⊥BC，交BC的延长线于H，

∵AD∥BC，

∴∠ADC=∠DCH，即∠ADP+∠PDG=∠DCQ+∠QCH，

∵PD∥CQ，

∴∠PDC=∠DCQ，

∴∠ADP=∠QCH，

又∵PD=CQ，

∴Rt△ADP≌Rt△HCQ，

∴AD=HC，

∵AD=1，BC=3，

∴BH=4，

∴当PQ⊥AB时，PQ的长最小，即为4.

问题3：如图3，设PQ与DC相交于点G，

∵PE∥CQ，PD=DE，

∴，

∴G是DC上一定点，

作QH⊥BC，交BC的延长线于H，

同理可证∠ADP=∠QCH，

∴Rt△ADP∽Rt△HCQ，

即，

∴CH=2，

∴BH=BG+CH=3+2=5，

∴當PQ⊥AB时，PQ的长最小，即为5.

问题4：如图4，设PQ与AB相交于点G，

∵PE∥BQ，AE=nPA，

∴，

作QH∥PD，交CB的延长线于H，过点C作CK⊥CD，交QH的延长线于K，

∵AD∥BC，AB⊥BC，

∴∠ADP=∠QHC，∠DAP+∠PAG=∠QBH+∠QBG=90°，∠PAG=∠QBG，

∴∠QBH=∠PAD，

∴△ADP∽△BHQ，

∴，

∵AD=1，

∴BH=n+1，

∴CH=BH+BC=3+n+1=n+4，

过点D作DM⊥BC于M，

则四边形ABND是矩形，

∴BM=AD=1，DM=AB=2

∴CM=BC-BM=3-1=2=DM，

∴∠DCM=45°，

∴∠KCH=45°，

∴CK=CH·cos45°= （n+4），

∴当PQ⊥CD时，PQ的长最小，最小值为（n+4）.

三、利用三角形三边关系

1.通过找到特殊定点构造三角形

例1.如图，∠MON=90°，边长为2的等边三角形ABC的顶点A、B分别在边OM，ON上当B在边ON上运动时，A随之在边OM上运动，等边三角形的形状保持不变，运动过程中，点C到点O的最大距离为（ ）

A.2.4 B. C. D.

试题分析：如图，取AB的中点D.连接CD.根据三角形的边角关系得到OC小于等于OD+DC，只有当O、D及C共线时，OC取得最大值，最大值为OD+CD。

【解答】解：如图，取AB的中点D，连接CD.

∵△ABC是等边三角形，且边长是2，∴BC=AB=2，

∵点D是AB边中点，

∴BD=AB=1，

∴CD===，即CD=；

连接OD，OC，有OC≤OD+DC，

当O、D、C共线时，OC有最大值，最大值是OD+CD，

由（1）得，CD=，

又∵△AOB为直角三角形，D为斜边AB的中点，

∴OD=AB=1，

∴OD+CD=1+，即OC的最大值为1+.

故选：C.

2.以旋转为背景构造三角形

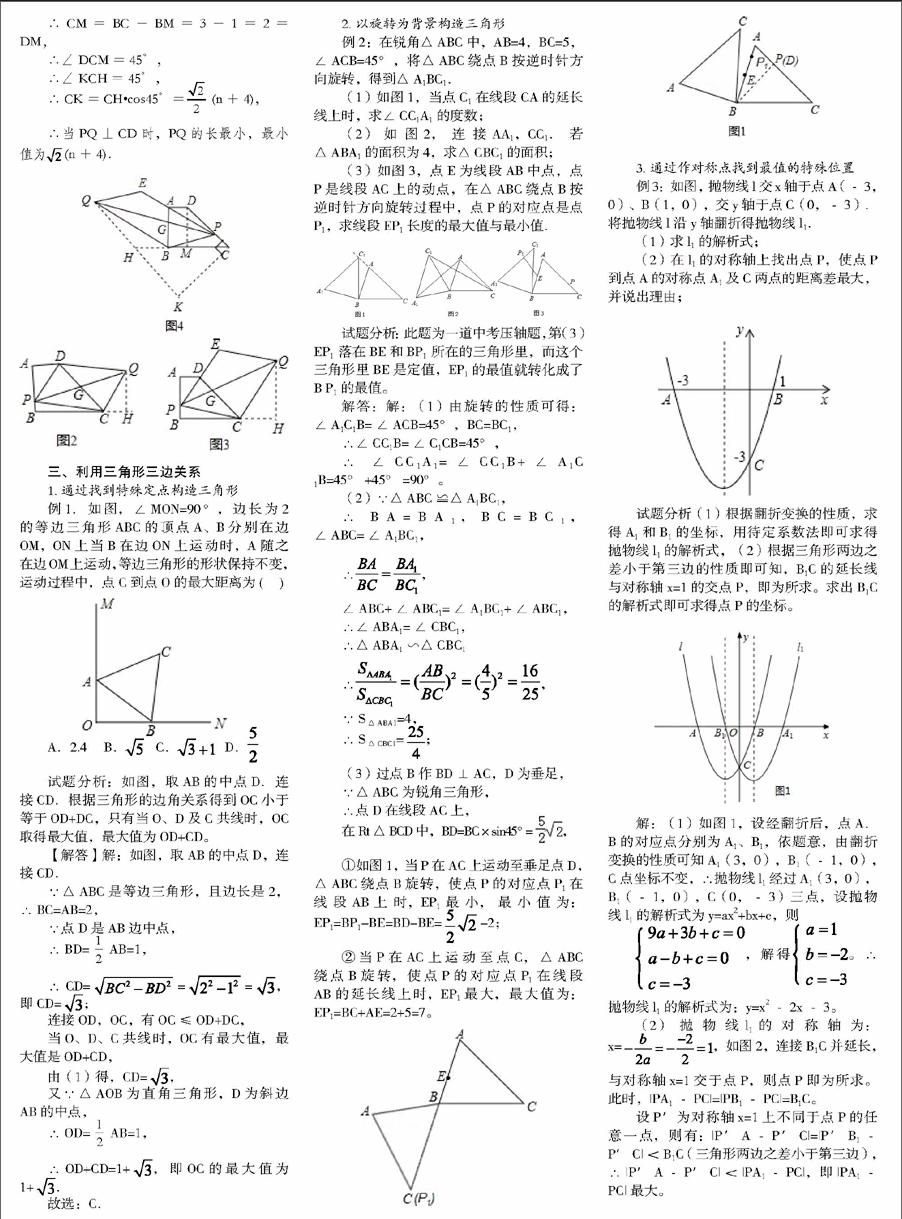
例2：在锐角△ABC中，AB=4，BC=5，∠ACB=45°，将△ABC绕点B按逆时针方向旋转，得到△A1BC1.

（1）如图1，当点C1在线段CA的延长线上时，求∠CC1A1的度数；

（2）如图2，连接AA1，CC1.若△ABA1的面积为4，求△CBC1的面积；

（3）如图3，点E为线段AB中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转过程中，点P的对应点是点P1，求线段EP1长度的最大值与最小值.

试题分析：此题为一道中考压轴题，第（3）EP1 落在BE和BP1 所在的三角形里，而这个三角形里BE是定值，EP1的最值就转化成了B P1 的最值。

解答：解：（1）由旋转的性质可得：∠A1C1B=∠ACB=45°，BC=BC1，

∴∠CC1B=∠C1CB=45°，

∴∠CC1A1=∠CC1B+∠A1C1B=45°+45°=90°。

（2）∵△ABC≌△A1BC1，

∴BA=BA1，BC=BC1，∠ABC=∠A1BC1，

∴，

∠ABC+∠ABC1=∠A1BC1+∠ABC1，

∴∠ABA1=∠CBC1，

∴△ABA1∽△CBC1

∴，

∵S△ABA1=4，

∴S△CBC1=；

（3）过点B作BD⊥AC，D为垂足，

∵△ABC为锐角三角形，

∴点D在线段AC上，

在Rt△BCD中，BD=BC×sin45°=，

①如图1，当P在AC上运动至垂足点D，△ABC绕点B旋转，使点P的对应点P1在线段AB上时，EP1最小，最小值为：EP1=BP1-BE=BD-BE=-2；

②当P在AC上运动至点C，△ABC绕点B旋转，使点P的对应点P1在线段AB的延长线上时，EP1最大，最大值为：EP1=BC+AE=2+5=7。

3.通过作对称点找到最值的特殊位置

例3：如图，抛物线l交x轴于点A（﹣3，0）、B（1，0），交y轴于点C（0，﹣3）.将抛物线l沿y轴翻折得抛物线l1.

（1）求l1的解析式；

（2）在l1的对称轴上找出点P，使点P到点A的对称点A1及C两点的距离差最大，并说出理由；

试题分析（1）根据翻折变换的性质，求得A1和B1的坐标，用待定系数法即可求得抛物线l1的解析式，（2）根据三角形两边之差小于第三边的性質即可知，B1C的延长线与对称轴x=1的交点P，即为所求。求出B1C的解析式即可求得点P的坐标。

解：（1）如图1，设经翻折后，点A.B的对应点分别为A1、B1，依题意，由翻折变换的性质可知A1（3，0），B1（﹣1，0），C点坐标不变，∴抛物线l1经过A1（3，0），B1（﹣1，0），C（0，﹣3）三点，设抛物线l1的解析式为y=ax2+bx+c，则

，解得。∴抛物线l1的解析式为：y=x2﹣2x﹣3。

（2）抛物线l1的对称轴为：x=，如图2，连接B1C并延长，与对称轴x=1交于点P，则点P即为所求。此时，|PA1﹣PC|=|PB1﹣PC|=B1C。

设P′为对称轴x=1上不同于点P的任意一点，则有：|P′A﹣P′C|=|P′B1﹣P′C|

设直线B1C的解析式为y=kx+b，则

，解得k=b=﹣3。∴直线B1C的解析式为：y=﹣3x﹣3。

令x=1，得y=﹣6。∴P（1，﹣6）。

通过以上三种类型题目的分析，我们不难发现，虽然线段最值及线段和差的最值是一个难点，但只要我们能够吃透本质，在碰到这种类型问题时都能结合具体题目具体分析，确定相应的类型，从而快速找到基本原理是利用两点之间线段最短，还是垂线段最短，抑或是利用三边关系。从而找到问题的突破口，去运用相关知识去解决这个难点。